Avrundning

Grafer över resultatet, y , av avrundning av x med olika metoder. För tydlighetens skull visas graferna förskjutna från heltals y -värden. Håll muspekaren över en metod i SVG-filen för att markera den och, i SMIL -aktiverade webbläsare, klicka för att välja eller avmarkera den.

Avrundning innebär att ersätta ett tal med ett ungefärligt värde som har en kortare, enklare eller mer explicit representation. Till exempel, ersätta $23,4476 med $23,45, bråkdelen 312/937 med 1/3 eller uttrycket √ 2 med 1,414.

Avrundning görs ofta för att få ett värde som är lättare att rapportera och kommunicera än originalet. Avrundning kan också vara viktigt för att undvika missvisande exakt rapportering av ett beräknat antal, mätning eller uppskattning; till exempel, en kvantitet som beräknades till 123 456 men som är känd för att vara korrekt endast inom några hundra enheter anges vanligtvis bättre som "ca 123 500".

Å andra sidan kommer avrundning av exakta tal att introducera ett visst avrundningsfel i det rapporterade resultatet. Avrundning är nästan oundviklig när man rapporterar många beräkningar – speciellt när man dividerar två tal i heltals- eller fastpunktsaritmetik ; vid beräkning av matematiska funktioner som kvadratrötter , logaritmer och sinus ; eller när du använder en flyttalsrepresentation med ett fast antal signifikanta siffror . I en sekvens av beräkningar ackumuleras dessa avrundningsfel i allmänhet och i vissa dåligt konditionerade fall kan de göra resultatet meningslöst.

Noggrann avrundning av transcendentala matematiska funktioner är svårt eftersom antalet extra siffror som behöver beräknas för att avgöra om man ska avrunda uppåt eller nedåt inte kan vara känt i förväg. Detta problem är känt som " bordsmakarens dilemma ".

Avrundning har många likheter med den kvantisering som sker när fysiska storheter måste kodas av siffror eller digitala signaler .

Ett vågigt likhetstecken ( ≈ : ungefär lika med ) används ibland för att indikera avrundning av exakta tal, t.ex. 9,98 ≈ 10. Detta tecken introducerades av Alfred George Greenhill 1892.

Idealiska egenskaper för avrundningsmetoder inkluderar:

Avrundning ska göras av en funktion . På detta sätt, när samma ingång avrundas i olika instanser, är utmatningen oförändrad.
Beräkningar som görs med avrundning bör ligga nära de som görs utan avrundning.
- Som ett resultat av (1) och (2) bör utdata från avrundning vara nära dess indata, ofta så nära som möjligt med någon metrik .
För att betraktas som avrundning kommer intervallet att vara en delmängd av domänen , i allmänhet diskret . Ett klassiskt område är heltal, Z .
Avrundning bör bevara symmetrier som redan finns mellan domänen och intervallet. Med ändlig precision (eller en diskret domän) översätts detta till att ta bort bias .
En avrundningsmetod bör vara användbar inom datavetenskap eller mänsklig aritmetik där ändlig precision används, och hastighet är ett övervägande.

Eftersom det vanligtvis inte är möjligt för en metod att uppfylla alla idealegenskaper, finns det många olika avrundningsmetoder.

Som en allmän regel är avrundning idempotent ; dvs, när ett tal väl har avrundats, kommer inte dess värde att ändras om du avrundar det igen. Avrundningsfunktioner är också monotona ; dvs att avrunda ett större tal ger ett större eller lika resultat än att avrunda ett mindre tal [ ^{förtydligande behövs ]} . I det allmänna fallet med ett diskret intervall är de konstanta funktioner styckevis .

Typer av avrundning

Typiska avrundningsproblem inkluderar:

Avrundningsproblem	Exempelinmatning	Resultat	Avrundningskriterium
Approximera ett irrationellt tal med en bråkdel	$π$	22/7	1-siffrig nämnare
Approximera ett rationellt tal med ett annat bråk med mindre täljare och nämnare	399/941	3/7	1-siffrig nämnare
Approximera ett bråk, som har periodisk decimalexpansion, med ett ändligt decimaltal	5/3	1,6667	4 decimaler
Ungefär ett decimaltal med bråktal med ett med färre siffror	2,1784	2.18	2 decimaler
Approximera ett decimalt heltal med ett heltal med fler efterföljande nollor	23 217	23 200	3 betydande siffror
Approximera ett stort decimalt heltal med hjälp av vetenskaplig notation	300 999 999	3,01 × 10 ⁸	3 betydande siffror
Approximera ett värde med en multipel av ett angivet belopp	48,2	45	Multipel av 15
Avrunda var och en av en ändlig uppsättning reella tal (mest bråk) till ett heltal (ibland det näst närmaste heltal) så att summan av de avrundade talen är lika med den avrundade summan av talen (som behövs t.ex. [1] för att fördela platser , implementerade t.ex. med den största resterande metoden , se Matematik för fördelning och [2] för att fördela den totala momsen för en faktura till dess poster)	{3/12, 4/12, 5/12}	{0, 0, 1}	Summan av avrundade element är lika med avrundad summa av element

Avrundning till heltal

Den mest grundläggande formen av avrundning är att ersätta ett godtyckligt tal med ett heltal. Alla följande avrundningslägen är konkreta implementeringar av en abstrakt "round()"-procedur med ett enda argument. Dessa är sanna funktioner (med undantag för de som använder slumpmässighet).

Riktad avrundning till ett heltal

Dessa fyra metoder kallas riktad avrundning , eftersom förskjutningarna från det ursprungliga talet x till det avrundade värdet y alla är riktade mot eller bort från samma gränsvärde (0, +∞ eller −∞). Riktad avrundning används i intervallaritmetik och krävs ofta i ekonomiska beräkningar.

Om x är positivt är avrundning ner detsamma som avrundning-mot-noll, och avrundning uppåt är detsamma som avrundning-bort-från-noll. Om x är negativt är avrundning nedåt detsamma som avrundning-bort-från-noll, och avrundning uppåt är detsamma som avrundning-mot-noll. I alla fall, om x är ett heltal, är y bara x .

Där många beräkningar görs i följd kan valet av avrundningsmetod ha en mycket betydande effekt på resultatet. Ett känt exempel gällde ett nytt index som upprättades av Vancouver Stock Exchange 1982. Det sattes ursprungligen till 1 000 000 (tre decimaler med noggrannhet) och hade efter 22 månader sjunkit till cirka 520 — medan aktiekurserna generellt sett hade ökat under perioden . Problemet orsakades av att indexet räknades om tusentals gånger dagligen, och alltid avrundades nedåt till 3 decimaler, på ett sådant sätt att avrundningsfelen ackumulerades. Omräkning med bättre avrundning gav ett indexvärde på 1098,892 vid slutet av samma period.

För exemplen nedan hänvisar $sgn(x) till$ teckenfunktionen som tillämpas på det ursprungliga numret, $x$ .

Avrundning nedåt

avrunda nedåt (eller ta ordet , eller avrunda mot negativ oändlighet ): y är det största heltal som inte överstiger x .
$y=\mathrm {floor} (x)=\left\lfloor x\right\rfloor =-\left\lceil - x\right\rceil$

Till exempel, 23,7 avrundas till 23, och −23,2 avrundas till −24.

Runda upp

avrunda uppåt (eller ta taket , eller avrunda mot positiv oändlighet ): y är det minsta heltal som inte är mindre än x .
$y=\operatörsnamn {tak} (x)=\left\lceil x\right\rceil =-\left\lfloor -x\right \rgolv$

Till exempel, 23,2 avrundas till 24, och −23,7 avrundas till −23.

Avrundning mot noll

avrunda mot noll (eller trunkera , eller avrunda bort från oändligheten ): y är det heltal som är närmast x så att det är mellan 0 och x (ingår); dvs y är heltalsdelen av x , utan dess bråksiffror.
$y=\operatörsnamn {truncate} (x)=\operatörsnamn {sgn}(x)\vänster\lgolv \vänster|x\höger|\höger\rgolv =-\operatörsnamn {sgn}(x)\left\lceil -\left|x\right|\right\rceil ={\begin{cases}\left\lfloor x\right\rfloor &x\geq 0\\\left \lceil x\right\rceil &x<0\\\end{cases}}$

Till exempel, 23,7 avrundas till 23, och −23,7 avrundas till −23.

Avrundning bort från noll

avrunda bort från noll (eller avrunda mot oändligheten ): y är det heltal som är närmast 0 (eller motsvarande x ) så att x är mellan 0 och y (ingår).
$y=\operatörsnamn {sgn}(x)\left\lceil \left|x\right|\right\rceil =-\operatörsnamn {sgn}(x )\left\lfloor -\left|x\right|\right\rfloor ={\begin{cases}\left\lceil x\right\rceil &x\geq 0\\\left\lfloor x\right\rfloor &x< 0\\\end{cases}}$

Till exempel, 23,2 avrundas till 24, och −23,2 avrundas till −24.

Avrundning till närmaste heltal

Att avrunda ett tal x till närmaste heltal kräver en oavgjort regel för de fall då x är exakt halvvägs mellan två heltal – det vill säga när bråkdelen av x är exakt 0,5.

Om det inte vore för 0,5 bråkdelar, skulle avrundningsfelen som introducerades av metoden avrundning till närmaste vara symmetriska: för varje bråkdel som avrundas nedåt (som 0,268) finns det en komplementär bråkdel (nämligen 0,732) som avrundas med samma belopp.

Vid avrundning av en stor uppsättning fixpunkttal med enhetligt fördelade bråkdelar, skulle avrundningsfelen med alla värden, med utelämnandet av de som har 0,5 bråkdelar, statistiskt kompensera varandra. Det betyder att det förväntade (medelvärde) värdet på de avrundade talen är lika med det förväntade värdet på de ursprungliga talen när tal med bråkdel 0,5 från mängden tas bort.

I praktiken används vanligtvis flyttal , som har ännu fler beräkningsnyanser eftersom de inte är lika fördelade.

Avrundar hälften uppåt

Följande oavgjort regel, kallad runda halva uppåt (eller runda halva mot positiv oändlighet ), används flitigt i många discipliner. ^{[ citat behövs ]} Det vill säga att halvvägsvärden på x alltid avrundas uppåt.

Om bråkdelen av x är exakt 0,5 så är y = x + 0,5
$y=\+left\lfloor 0.5\höger\rgolv =-\vänster\lceil -x-0.5\höger\rceil =\vänster\lceil {\frac {\lgolv 2x\rgolv}{2}}\höger\rceil$

Till exempel, 23,5 avrundas till 24, och −23,5 avrundas till −23.

Men vissa programmeringsspråk (som Java, Python) definierar sin halva upp som rund halva bort från noll här.

Denna metod kräver endast kontroll av en siffra för att bestämma avrundningsriktningen i tvås komplement och liknande representationer.

Avrundar hälften nedåt

Man kan också använda rund halv ner (eller rund halv mot negativ oändlighet ) i motsats till den vanligare runda halva uppåt .

Om bråkdelen av x är exakt 0,5 så är y = x − 0,5
$yil=\x-\lce 0.5\höger\rceil =-\vänster\lgolv -x+0.5\höger\rgolv =\vänster\lgolv {\frac {\lceil 2x\rceil }{2}}\höger\rgolv$

Till exempel, 23,5 avrundas till 23 och −23,5 avrundas till −24.

Men vissa programmeringsspråk (som Java, Python) definierar sin halva ner som rund halva mot noll här.

Avrundar hälften mot noll

Man kan också runda hälften mot noll (eller avrunda hälften bort från oändligheten ) i motsats till den konventionella rundan hälften bort från noll .

Om bråkdelen av x är exakt 0,5, då är y = x − 0,5 om x är positivt, och y = x + 0,5 om x är negativ.
$y=\operatörsnamn {sgn}(x)\left\lceil \left|x\right|-0.5\right\rceil =-\operatörsnamn {sgn}(x)\left\lfloor -\left |x\right|+0.5\höger\rgolv$

Till exempel, 23,5 avrundas till 23, och −23,5 avrundas till −23.

Denna metod behandlar positiva och negativa värden symmetriskt och är därför fri från övergripande positiva/negativa bias om de ursprungliga talen är positiva eller negativa med lika sannolikhet. Den har dock fortfarande fördom mot noll.

Avrundar hälften bort från noll

Den andra oavgjorda metoden som vanligtvis lärs ut och används är den runda halvan bort från noll (eller den runda halvan mot oändligheten ), nämligen:

Om bråkdelen av x är exakt 0,5, då är y = x + 0,5 om x är positivt, och y = x − 0,5 om x är negativ.
$y=\operatörsnamn {sgn}(x)\left\lfloor \left|x\right|+0,5\right\rfloor =-\operatörsnamn {sgn}(x)\left\lceil -\left |x\right|-0.5\right\rceil$

Till exempel, 23,5 avrundas till 24 och −23,5 avrundas till −24.

Detta kan vara mer effektivt på binära datorer eftersom endast den första utelämnade biten behöver beaktas för att avgöra om den avrundas uppåt (på en 1) eller nedåt (på en 0). Detta är en metod som används vid avrundning till signifikanta siffror på grund av dess enkelhet.

Denna metod, även känd som kommersiell avrundning ^{. , positiva} behandlar och negativa värden symmetriskt och är därför fri från övergripande positiva/negativa bias om de ursprungliga talen är positiva eller negativa med lika sannolikhet Den har dock fortfarande fördom från noll.

Det används ofta för valutaomvandlingar och prisavrundningar (när beloppet först omvandlas till den minsta betydande underavdelningen av valutan, såsom cent av en euro) eftersom det är lätt att förklara genom att bara beakta den första bråksiffran, oberoende av tilläggssiffran precisionssiffror eller tecken på beloppet (för strikt likvärdighet mellan den betalande och mottagaren av beloppet).

Avrundar hälften till jämnt

En oavgjort regel utan positiv/negativ bias och utan bias mot/bort från noll är rund halv till jämn . Enligt denna konvention, om bråkdelen av x är 0,5, så är y det jämna heltal närmast x . Således, till exempel, +23,5 blir +24, liksom +24,5; dock blir −23,5 −24, liksom −24,5. Denna funktion minimerar det förväntade felet vid summering över avrundade siffror, även när ingångarna är mestadels positiva eller mestadels negativa, förutsatt att de varken är oftast jämna eller mestadels udda.

Denna variant av avrundning-till-närmaste-metoden kallas även konvergent avrundning , statistikeravrundning , holländsk avrundning , Gaussavrundning , udda–jämn avrundning eller bankavrundning .

Detta är standardavrundningsläget som används i IEEE 754- operationer för resultat i binära flyttalsformat, och det mer sofistikerade läget [ ^{förtydligande behövs ]} som används vid avrundning till signifikanta siffror.

Genom att eliminera bias kommer upprepad addition eller subtraktion av oberoende tal, som i en endimensionell slumpmässig gång , att ge ett avrundat resultat med ett fel som tenderar att växa i proportion till kvadratroten av antalet operationer snarare än linjärt.

Den här regeln snedvrider dock fördelningen genom att öka sannolikheten för jämnheter i förhållande till odds. Vanligtvis är detta mindre viktigt ^{[ citat behövs ]} än de fördomar som elimineras med denna metod.

Avrunda hälften till udda

En liknande oavgjort regel för att runda halv till jämn är rund halv till udda . I detta tillvägagångssätt, om bråkdelen av x är 0,5, så är y det udda heltal närmast x . Således, till exempel, +23,5 blir +23, liksom +22,5; medan −23,5 blir −23, liksom −22,5.

Denna metod är också fri från positiv/negativ bias och bias mot/bort från noll, förutsatt att talen som ska avrundas varken är oftast jämna eller oftast udda. Det delar också den runda halva till jämna egenskapen att förvränga den ursprungliga fördelningen, eftersom den ökar sannolikheten för odds i förhållande till jämna.

Denna variant används nästan aldrig i beräkningar, förutom i situationer där man vill undvika att öka skalan för flyttal, som har ett begränsat exponentomfång. Med avrunda hälften till jämnt skulle ett icke-oändligt tal avrundas till oändligt, och ett litet denormalt värde skulle avrundas till ett normalt värde som inte är noll. I själva verket föredrar detta läge att bevara den befintliga skalan av jämna tal, och undviker resultat utanför intervallet när det är möjligt för siffersystem med jämn radix (som binär och decimal). ^{[ förtydligande behövs (se diskussion ) ]}

Avrundning för att förbereda för kortare precision

Detta avrundningsläge (RPSP i det här kapitlet) används för att undvika att få fel resultat med dubbel (inklusive multipel) avrundning. Med detta avrundningsläge kan man undvika fel resultat efter dubbel avrundning, om alla avrundningar utom den sista görs med RPSP, och endast slutavrundning använder det externt begärda läget.

Med decimalaritmetik, om det finns ett val mellan tal med den minsta signifikanta siffran 0 eller 1, 4 eller 5, 5 eller 6, 9 eller 0, ska siffran som skiljer sig från 0 eller 5 väljas; annars är valet godtyckligt. IBM definierar att i det senare fallet ska en siffra med den mindre storleken väljas. RPSP kan tillämpas med steget mellan två på varandra följande avrundningar så litet som en enda siffra (till exempel kan avrundning till 1/10 tillämpas efter avrundning till 1/100). Till exempel, när man avrundar till heltal,

20,0 avrundas till 20;
20.01, 20.1, 20.9, 20.99, 21, 21.01, 21.9, 21.99 avrundas till 21;
22,0, 22,1, 22,9, 22,99 avrundas till 22;
24,0, 24,1, 24,9, 24,99 avrundas till 24;
25,0 avrundas till 25;
25.01, 25.1 avrundas till 26.

I exemplet från avsnittet " Dubbel avrundning " ger avrundning 9,46 till en decimal 9,4, vilken avrundning till heltal i sin tur ger 9.

Med binär aritmetik görs avrundningen som "runda till udda" (inte blandas med " runda hälften till udda ".) Till exempel när man avrundar till 1/4:

x == 2,0 => resultatet är 2
2,0 < x < 2,5 => resultatet är 2,25
x == 2,5 => resultatet är 2,5
2,5 < x < 3,0 => resultatet är 2,75
x == 3,0 => resultatet är 3,0

För korrekta resultat ska RPSP tillämpas med steget på minst 2 binära siffror, annars kan fel resultat visas. Till exempel,

3,125 RPSP till 1/4 => resultatet är 3,25
3,25 RPSP till 1/2 => resultatet är 3,5
3,5 runda-halv-till-jämn till 1 => resultatet är 4 (fel)

Om steget är 2 bitar eller mer, ger RPSP 3,25, vilket i sin tur, avrunda hälften till jämnt till heltal, resulterar i 3.

RPSP är implementerat i hårdvara i IBM zSeries och pSeries .

Randomiserad avrundning till ett heltal

Omväxlande tie-breaking

En metod, mer oklar än de flesta, är att växla riktning när man avrundar ett tal med 0,5 bråkdel. Alla andra är avrundade till närmaste heltal.

Närhelst bråkdelen är 0,5, alternativ avrundning uppåt eller nedåt: för den första förekomsten av en 0,5-bråkdel, avrunda uppåt, för den andra förekomsten, avrunda nedåt och så vidare. Alternativt kan den första 0,5 bråkdelsavrundningen bestämmas av ett slumpmässigt frö . "Upp" och "ner" kan vara vilka två avrundningsmetoder som helst som motsätter sig varandra - mot och bort från positiv oändlighet eller mot och bort från noll.

Om förekomster av 0,5 bråkdelar inträffar betydligt mer än en omstart av förekomsten "räknande", så är det i praktiken biasfritt. Med garanterad nollbias är det användbart om talen ska summeras eller medelvärdesbildas.

Slumpmässig tie-breaking

Om bråkdelen av x är 0,5, välj y slumpmässigt mellan x + 0,5 och x − 0,5 , med lika sannolikhet. Alla andra är avrundade till närmaste heltal.

Liksom runda-halva-till-jämn och runda-halva-till-udda är denna regel i princip fri från övergripande fördomar, men den är också rättvis bland jämna och udda y- värden . En fördel jämfört med alternativ tie-breaking är att den sista avrundningsriktningen på 0,5 bråkdelen inte behöver "kommas ihåg".

Stokastisk avrundning

Avrundning enligt följande till ett av de närmaste heltal mot negativ oändlighet och det närmaste heltal mot positiv oändlighet, med en sannolikhet som beror på närheten kallas stokastisk avrundning och ger ett opartiskt resultat i genomsnitt.

\} (operatornamn x)={\begin{fall}\lgolv x\rgolv &{\text{ med sannolikhet }}1-(x-\lgolv x\rgolv)=\lgolv x\rgolv -x+1\\\lgolv x\ rfloor +1&{\text{ med sannolikhet }}{x-\lfloor x\rfloor }\end{cases}}

Till exempel skulle 1,6 avrundas till 1 med sannolikhet 0,4 och till 2 med sannolikhet 0,6.

Stokastisk avrundning kan vara korrekt på ett sätt som en avrundningsfunktion aldrig kan vara. Anta till exempel att man började med 0 och lade till 0,3 till det hundra gånger samtidigt som man avrundar den löpande summan mellan varje tillägg. Resultatet skulle bli 0 med vanlig avrundning, men med stokastisk avrundning skulle det förväntade resultatet bli 30, vilket är samma värde som erhålls utan avrundning. Detta kan vara användbart vid maskininlärning där utbildningen kan använda aritmetik med låg precision iterativt. Stokastisk avrundning är också ett sätt att uppnå 1-dimensionell vibrering .

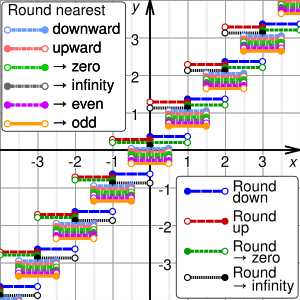
Jämförelse av metoder för avrundning till ett heltal

Värde	Funktionella metoder											Randomiserade metoder
	Riktad avrundning				Runda till närmaste						Runda för att förbereda för kortare precision	Omväxlande tie-break		Slumpmässig tie-break		Stokastisk
	Ner (mot − ∞ )	Uppåt (mot + ∞ )	Mot 0	Bort från 0	Halv ner (mot − ∞ )	Halvt upp (mot + ∞ )	Hälften mot 0	Halvvägs från 0	Hälften till Even	Hälften till Odd	Runda för att förbereda för kortare precision	Genomsnitt	SD	Genomsnitt	SD	Genomsnitt	SD
+1,8	+1	+2	+1	+2	+2	+2	+2	+2	+2	+2	+1	+2	0	+2	0	+1,8	0,04
+1,5					+1	+2	+1	+2	+2	+1		+1,505	0	+1,5	0,05	+1,5	0,05
+1,2						+1		+1	+1			+1	0	+1	0	+1,2	0,04
+0,8	0	+1	0	+1					+1			+1	0	+1	0	+0,8	0,04
+0,5					0		0		0			+0,505	0	+0,5	0,05	+0,5	0,05
+0,2						0		0		0		0	0	0	0	+0,2	0,04
−0,2	−1	0		−1				0		0	−1	0	0	0	0	−0,2	0,04
−0,5					−1			−1		−1		-0,495	0	−0,5	0,05	−0,5	0,05
−0,8						−1	−1		−1			−1	0	−1	0	−0,8	0,04
−1.2	−2	−1	−1	−2					−1			−1	0	−1	0	−1.2	0,04
−1,5					−2			−2	−2			−1,495	0	−1,5	0,05	−1,5	0,05
−1.8					−2	−2	−2	−2	−2	−2		−2	0	−2	0	−1.8	0,04

Avrundning till andra värden

Avrundning till en angiven multipel

Den vanligaste typen av avrundning är att avrunda till ett heltal; eller, mer allmänt, till en heltalsmultipel av något inkrement — såsom avrundning till hela tiondelar av sekunder, hundradelar av en dollar, till hela multiplar av 1/2 eller 1/8 tum, till hela dussintals eller tusentals, etc.

I allmänhet innebär att avrunda ett tal x till en multipel av något specificerat positivt värde m följande steg:

\mathrm {roundToMultiple} (x,m)=\mathrm { rund} (x/m)\ gånger m

Till exempel, avrundning av x = 2,1784 dollar till hela cent (dvs. till en multipel av 0,01) innebär att man beräknar 2,1784 / 0,01 = 217,84, sedan avrundar det till 218, och slutligen beräknas 218 × 0,01 = 2,18.

Vid avrundning till ett förutbestämt antal signifikanta siffror beror ökningen m på storleken på talet som ska avrundas (eller på det avrundade resultatet).

Ökningen m är normalt en finit bråkdel i vilket siffersystem som helst som används för att representera talen. För visning för människor betyder det vanligtvis det decimala siffersystemet (det vill säga, m är ett heltal gånger en potens av 10, som 1/1000 eller 25/100). För mellanvärden lagrade i digitala datorer betyder det ofta det binära siffersystemet ( m är ett heltal gånger en potens av 2).

Den abstrakta enargumentfunktionen "round()" som returnerar ett heltal från ett godtyckligt reellt värde har minst ett dussin distinkta konkreta definitioner som presenteras i avsnittet avrundning till heltal . Den abstrakta tvåargumentfunktionen "roundToMultiple()" definieras formellt här, men i många fall används den med det implicita värdet m = 1 för inkrementet och reduceras sedan till den ekvivalenta abstrakta enargumentfunktionen, med också samma dussin tydliga konkreta definitioner.

Logaritmisk avrundning

Avrundning till en specificerad effekt

Avrundning till en specificerad potens skiljer sig mycket från avrundning till en specificerad multipel ; till exempel är det vanligt i datorer att behöva avrunda ett tal till en hel potens av 2. Stegen, i allmänhet, för att avrunda ett positivt tal x till en potens av något positivt tal b annat än 1, är:

\mathrm {roundToPower} (x ,b)=b^{\mathrm {runda} (\log _{b}x)},x>0,b>0,b\neq 1

Många av varningarna som gäller för avrundning till en multipel är tillämpliga på avrundning till en potens.

Skalad avrundning

Denna typ av avrundning, som också kallas avrundning till en logaritmisk skala , är en variant av avrundning till en angiven potens . Avrundning på en logaritmisk skala åstadkoms genom att ta loggen av mängden och göra normal avrundning till närmaste värde på log-skalan.

Till exempel levereras motstånd med föredragna siffror på en logaritmisk skala. Speciellt för motstånd med 10 % noggrannhet levereras de med nominella värden 100, 120, 150, 180, 220, etc. avrundade till multiplar av 10 (E12-serien ) . Om en beräkning indikerar att ett motstånd på 165 ohm krävs då log(150) = 2,176, log(165) = 2,217 och log(180) = 2,255. Logaritmen 165 är närmare logaritmen 180, därför skulle ett 180 ohm motstånd vara förstahandsvalet om det inte finns några andra överväganden.

Huruvida ett värde $x \in (a, b)$ avrundas till a eller b beror på om det kvadratiska värdet $x 2$ är större än eller mindre än produkten $ab$ . Värdet 165 avrundas till 180 i resistorexemplet eftersom $1652 = 27225$ är större än $150 \times 180 = 27000$ .

Flytpunktsavrundning

I flyttalsaritmetik syftar avrundning till att förvandla ett givet värde x till ett värde y med ett specificerat antal signifikanta siffror. Med andra ord y vara en multipel av ett tal m som beror på storleken på x . Talet m är en potens av basen (vanligtvis 2 eller 10) av flyttalsrepresentationen.

Förutom denna detalj, gäller alla varianter av avrundning som diskuterats ovan även för avrundning av flyttal. Algoritmen för sådan avrundning presenteras i Skalad avrundning ovan, men med en konstant skalfaktor s = 1 och en heltalsbas b > 1.

Där det avrundade resultatet skulle svämma över är resultatet för en riktad avrundning antingen den lämpliga oändligheten med tecken vid "avrundning från noll", eller det högsta representativa positiva ändliga talet (eller det lägsta representativa negativa ändliga talet om x är negativt), när " avrundning " mot noll". Resultatet av ett spill för det vanliga fallet av runda till närmaste är alltid den lämpliga oändligheten.

Avrundning till en enkel bråkdel

I vissa sammanhang är det önskvärt att avrunda ett givet tal x till ett "snyggt" bråk - det vill säga det närmaste bråket y = m / n vars täljare m och nämnare n inte överstiger ett givet maximum. Detta problem skiljer sig ganska mycket från det att avrunda ett värde till ett fast antal decimala eller binära siffror, eller till en multipel av en given enhet m . Detta problem är relaterat till Farey-sekvenser , Stern-Brocot-trädet och fortsatta fraktioner .

Avrundning till ett tillgängligt värde

Färdigt timmer , skrivpapper, kondensatorer och många andra produkter säljs vanligtvis endast i ett fåtal standardstorlekar.

Många designprocedurer beskriver hur man beräknar ett ungefärligt värde och sedan "avrundar" till någon standardstorlek med hjälp av fraser som "runda ner till närmaste standardvärde", "runda upp till närmaste standardvärde" eller "runda till närmaste standardvärde" .

När en uppsättning föredragna värden är jämnt fördelade på en logaritmisk skala, kan valet av det föredragna värdet närmast ett givet värde ses som en form av skalad avrundning . Sådana avrundade värden kan beräknas direkt.

Avrundning i andra sammanhang

Dithering och felspridning

Vid digitalisering av kontinuerliga signaler , såsom ljudvågor, är den totala effekten av ett antal mätningar viktigare än exaktheten i varje enskild mätning. Under dessa omständigheter används normalt rastrering och en relaterad teknik, error diffusion . En relaterad teknik som kallas pulsbreddsmodulering används för att uppnå analog typutgång från en tröghetsanordning genom att snabbt pulsa effekten med en variabel arbetscykel.

Felspridning försöker säkerställa att felet i genomsnitt minimeras. När man har att göra med en svag lutning från ett till noll, skulle utmatningen vara noll under de första termerna tills summan av felet och det aktuella värdet blir större än 0,5, i vilket fall en 1 matas ut och skillnaden subtraheras från felet än så länge. Floyd–Steinberg-dithering är ett populärt felspridningsförfarande vid digitalisering av bilder.

Som ett endimensionellt exempel, anta att talen 0,9677 , 0,9204 , 0,7451 och 0,3091 förekommer i ordning och var och en ska avrundas till en multipel av 0,01 . I det här fallet är de kumulativa summorna 0,9677 , 1,8881 = 0,9677 + 0,9204 , 2,6332 = 0,9677 + 0,9204 + 0,7451 och 2,9423 = 0,9677 + 40 vardera, 0,9677 + 40 . avrundat till en multipel av 0,01 : 0,97 , 1,89 , 2,63 och 2,94 . Den första av dessa och skillnaderna mellan intilliggande värden ger de önskade avrundade värdena: 0,97 , 0,92 = 1,89 − 0,97 , 0,74 = 2,63 − 1,89 och 0,31 = 2,94 − 2,63 .

Monte Carlo aritmetik

Monte Carlo aritmetik är en teknik i Monte Carlo metoder där avrundningen sker slumpmässigt uppåt eller nedåt. Stokastisk avrundning kan användas för Monte Carlo aritmetik, men i allmänhet används bara avrundning uppåt eller nedåt med lika sannolikhet oftare. Upprepade körningar kommer att ge en slumpmässig fördelning av resultat som kan indikera stabiliteten i beräkningen.

Exakt beräkning med avrundad aritmetik

Det är möjligt att använda avrundad aritmetik för att utvärdera det exakta värdet av en funktion med heltalsdomän och intervall. Till exempel, om ett heltal n är känt för att vara en perfekt kvadrat, kan dess kvadratrot beräknas genom att konvertera n till ett flyttalsvärde z , beräkna den ungefärliga kvadratroten x ur z med flyttal, och sedan avrunda x till närmaste heltal y . Om n inte är för stort, kommer flyttalsavrundningsfelet i x att vara mindre än 0,5, så det avrundade värdet y blir den exakta kvadratroten ur n . Detta är i grunden varför diaregler kan användas för exakt aritmetik.

Dubbel avrundning

Att avrunda ett tal två gånger i följd till olika precisionsnivåer, där den senare precisionen är grövre, är inte garanterat att ge samma resultat som att avrunda en gång till den slutliga precisionen förutom i fallet med riktad avrundning. Till exempel ger avrundning 9,46 till en decimal 9,5, och sedan 10 när man avrundar till heltal genom att avrunda hälften till jämnt, men skulle ge 9 när man avrundar till heltal direkt. Borman och Chatfield diskuterar implikationerna av dubbel avrundning när man jämför data avrundade till en decimal med specifikationsgränser uttryckta med heltal.

I Martinez v. Allstate och Sendejo v. Farmers , som tvistades mellan 1995 och 1997, hävdade försäkringsbolagen att dubbla avrundningspremier var tillåtna och i själva verket krävdes. De amerikanska domstolarna dömde mot försäkringsbolagen och beordrade dem att anta regler för att säkerställa en enda avrundning.

Vissa datorspråk och standarden IEEE 754-2008 föreskriver att resultatet inte ska avrundas två gånger i enkla beräkningar. Detta har varit ett särskilt problem med Java eftersom det är designat för att köras identiskt på olika maskiner, speciella programmeringsknep har behövt användas för att uppnå detta med x87 flyttal. Java-språket ändrades för att tillåta olika resultat där skillnaden inte spelar någon roll och kräver att en strictfp- kvalificering används när resultaten måste överensstämma korrekt; strikt flyttal har återställts i Java 17.

I vissa algoritmer beräknas ett mellanresultat med större precision och måste sedan avrundas till den slutliga precisionen. Dubbel avrundning kan undvikas genom att välja en lämplig avrundning för den mellanliggande beräkningen. Detta består i att undvika att runda till mittpunkten för den sista avrundningen (förutom när mittpunkten är exakt). I binär aritmetik är tanken att avrunda resultatet mot noll och sätta den minst signifikanta biten till 1 om det avrundade resultatet är inexakt; denna avrundning kallas klibbig avrundning . På motsvarande sätt består det i att returnera det mellanliggande resultatet när det är exakt representativt, och det närmaste flyttalstalet med en udda signifikans och annars; det är därför det också är känt som avrundning till udda . En konkret implementering av detta tillvägagångssätt, för binär och decimal aritmetik, implementeras som avrundning för att förbereda för kortare precision .

Bordsmakarens dilemma

William M. Kahan myntade termen "The Table-Maker's Dilemma" för den okända kostnaden för att avrunda transcendentala funktioner :

Ingen vet hur mycket det skulle kosta att beräkna y ^w korrekt avrundat för vartannat flyttalsargument där det inte över-/underflyter. Istället beräknar välrenommerade mattebibliotek elementära transcendentala funktioner mestadels inom något mer än en halv ulp och nästan alltid väl inom en ulp. Varför kan du ^avrundas inte inom en halv ulp som SQRT? Eftersom ingen vet hur mycket beräkning det skulle kosta... Det finns inget allmänt sätt att förutsäga hur många extra siffror som kommer att behöva bäras för att beräkna ett transcendentalt uttryck och avrunda det korrekt till något förutbestämt antal siffror. Även det faktum (om sant) att ett ändligt antal extra siffror i slutändan kommer att räcka kan vara ett djupt teorem.

Flyttalsstandarden IEEE 754 garanterar att addera, subtrahera, multiplicera, dividera, sammansmält multiplicera –lägg till , kvadratrot och flyttalsrest kommer att ge det korrekt avrundade resultatet av operationen med oändlig precision. Ingen sådan garanti gavs i 1985 års standard för mer komplexa funktioner och de är vanligtvis bara korrekta inom den sista biten i bästa fall. Men 2008 års standard garanterar att överensstämmande implementeringar ger korrekt avrundade resultat som respekterar det aktiva avrundningsläget; implementering av funktionerna är dock frivillig.

Genom att använda Gelfond-Schneider-satsen och Lindemann-Weierstrass-satsen kan många av de vanliga elementära funktionerna bevisas ge transcendentala resultat, förutom på några välkända argument; ur en teoretisk synvinkel är det därför alltid möjligt att korrekt runda sådana funktioner. Men för en implementering av en sådan funktion kan det kräva mycket beräkningstid eller vara utom räckhåll att bestämma en gräns för en given precision för hur exakta resultat som behöver beräknas innan ett korrekt avrundat resultat kan garanteras. I praktiken, när denna gräns inte är känd (eller bara en mycket stor gräns är känd), måste något beslut fattas vid implementeringen (se nedan). men enligt en sannolikhetsmodell kan korrekt avrundning tillfredsställas med mycket hög sannolikhet när man använder en mellannoggrannhet på upp till två gånger antalet siffror i målformatet plus någon liten konstant (efter att man tagit hänsyn till specialfall).

Vissa programmeringspaket erbjuder korrekt avrundning. GNU MPFR -paketet ger korrekt avrundade godtyckliga precisionsresultat. Vissa andra bibliotek implementerar elementära funktioner med korrekt avrundning i dubbel precision:

IBMs ml4j , som står för Mathematical Library for Java , skriven av Abraham Ziv och Moshe Olshansky 1999, korrekt avrundad till enbart närmaste . Detta bibliotek påstods vara portabelt, men endast binärfiler för PowerPC / AIX , SPARC / Solaris och x86 / Windows NT tillhandahölls. Enligt dess dokumentation använder detta bibliotek ett första steg med en noggrannhet som är lite större än dubbel precision, ett andra steg baserat på dubbel-dubbel aritmetik och ett tredje steg med en 768-bitars precision baserat på matriser med IEEE 754 dubbel precision flyttalstal.
IBMs exakta portabla matematiska bibliotek (förkortat APMathLib eller bara MathLib), även kallat libultim, avrundas endast till närmaste. Detta bibliotek använder upp till 768 bitars arbetsprecision. Det inkluderades i GNU C-biblioteket 2001, men de "långsamma banorna" (som ger korrekt avrundning) togs bort från 2018 till 2021.
Sun Microsystems libmcr, i de 4 avrundningslägena. För de svåra fallen använder det här biblioteket också multipel precision, och antalet ord ökas med 2 varje gång bordsmakarens dilemma inträffar (med odefinierat beteende i den mycket osannolika händelsen att någon gräns för maskinen nås).
CRlibm, skrivet i det gamla Arénaire-teamet (LIP, ENS Lyon ) . Den stöder de 4 avrundningslägena och är bevisad med hjälp av kunskapen om de svåraste fallen.
CORE-MATH-projektet ger några korrekt avrundade funktioner i de 4 avrundningslägena, med hjälp av kunskapen om de svåraste fallen.

Det finns beräkningsbara tal för vilka ett avrundat värde aldrig kan bestämmas oavsett hur många siffror som beräknas. Specifika exempel kan inte ges men detta följer av det oavgjorda att stoppa problemet . Till exempel, om Goldbachs gissning är sann men obevisbar , så kan resultatet av att avrunda följande värde upp till nästa heltal inte bestämmas: antingen 1+10 ^{− n} där n är det första jämna talet större än 4 som inte är summan av två primtal, eller 1 om det inte finns något sådant tal. Det avrundade resultatet är 2 om ett sådant tal n finns och 1 annars. Värdet före avrundning kan dock approximeras till vilken precision som helst även om gissningen är obevisbar.

Interaktion med strängsökningar

Avrundning kan negativt påverka en strängsökning efter ett nummer. Till exempel $π$ avrundad till fyra siffror "3.1416", men en enkel sökning efter denna sträng kommer inte att upptäcka "3.14159" eller något annat värde på $π$ avrundat till mer än fyra siffror. Däremot lider inte trunkering av detta problem; till exempel, en enkel strängsökning efter "3.1415", som är $π$ trunkerad till fyra siffror, kommer att upptäcka värden på $π$ trunkerad till mer än fyra siffror.

Historia

Begreppet avrundning är mycket gammalt, kanske äldre än själva uppdelningsbegreppet. Vissa forntida lertavlor som hittats i Mesopotamien innehåller tabeller med avrundade värden på reciproka och kvadratrötter i bas 60. Avrundade approximationer till $π$ , årets längd och månadens längd är också gamla – se exempel på bas 60 .

Runda -till-jämn- metoden har fungerat som ASTM (E-29)-standard sedan 1940. Ursprunget till termerna opartisk avrundning och statistikerns avrundning är ganska självförklarande. I 1906 års fjärde upplaga av Probability and Theory of Errors kallade Robert Simpson Woodward detta för "datorns regel" vilket indikerar att det då var allmänt brukat av mänskliga datorer som beräknade matematiska tabeller. Churchill Eisenhart indikerade att praktiken redan var "väl etablerad" i dataanalys på 1940-talet.

Ursprunget till termen bankers avrundning är fortfarande mer oklar. Om denna avrundningsmetod någonsin varit en standard inom bankväsendet har bevisen visat sig vara extremt svåra att hitta. Tvärtom antyder avsnitt 2 i Europeiska kommissionens rapport The Introduction of the Euro and the Rounding of Currency Amounts att det tidigare inte hade funnits någon standardmetod för avrundning inom bankverksamhet; och det specificerar att "halvvägs" belopp ska avrundas uppåt.

Fram till 1980-talet fixades den avrundningsmetoden som användes i aritmetiken med flyttalsdator vanligtvis av hårdvaran, dåligt dokumenterad, inkonsekvent och olika för varje märke och modell av dator. Denna situation förändrades efter att flyttalsstandarden IEEE 754 antogs av de flesta datortillverkare. Standarden tillåter användaren att välja mellan flera avrundningslägen och anger i varje fall exakt hur resultaten ska avrundas. Dessa funktioner gjorde numeriska beräkningar mer förutsägbara och maskinoberoende, och möjliggjorde en effektiv och konsekvent implementering av intervallaritmetik .

För närvarande tenderar mycket forskning att avrunda till multiplar av 5 eller 2. Till exempel använde Jörg Baten åldershop i många studier för att utvärdera räknenivån hos forntida befolkningar. Han kom med ABCC-indexet , som gör det möjligt att jämföra räknefärdigheter mellan regioner utan några historiska källor där befolkningens läskunnighet mättes.

Avrundningsfunktioner i programmeringsspråk

De flesta programmeringsspråk tillhandahåller funktioner eller speciell syntax för att runda bråktal på olika sätt. De tidigaste numeriska språken, såsom FORTRAN och C , skulle endast tillhandahålla en metod, vanligtvis trunkering (mot noll). Denna standardmetod kan antydas i vissa sammanhang, till exempel när man tilldelar ett bråktal till en heltalsvariabel eller använder ett bråktal som ett index för en matris . Andra typer av avrundning måste programmeras explicit; till exempel kan avrundning av ett positivt tal till närmaste heltal implementeras genom att lägga till 0,5 och trunkering.

Under de senaste decennierna har dock syntaxen och standardbiblioteken för de flesta språk vanligtvis tillhandahållit åtminstone de fyra grundläggande avrundningsfunktionerna (upp, ner, till närmaste och mot noll). Den oavgjorda metoden kan variera beroende på språk och version eller kan väljas av programmeraren. Flera språk följer ledningen av flyttalstandarden IEEE 754 och definierar dessa funktioner som att ta ett dubbelprecisionsflytargument och returnera resultatet av samma typ, som sedan kan konverteras till ett heltal vid behov. Detta tillvägagångssätt kan undvika falska spill eftersom flyttalstyper har ett större intervall än heltalstyper. Vissa språk, som PHP , tillhandahåller funktioner som avrundar ett värde till ett visst antal decimalsiffror (t.ex. från 4321.5678 till 4321.57 eller 4300). Dessutom tillhandahåller många språk en printf eller liknande strängformateringsfunktion, som gör att man kan konvertera ett bråktal till en sträng, avrundat till ett användarspecificerat antal decimaler (precisionen ) . Å andra sidan är trunkering (avrundning till noll) fortfarande standardavrundningsmetoden som används av många språk, speciellt för uppdelning av två heltalsvärden.

Däremot definierar inte CSS och SVG någon specifik maximal precision för siffror och mätningar, som de behandlar och exponerar i deras DOM och i deras IDL- gränssnitt som strängar som om de hade oändlig precision , och skiljer inte mellan heltal och flyttal. värden; Men implementeringarna av dessa språk kommer vanligtvis att konvertera dessa siffror till IEEE 754 flyttalsvärden med dubbel precision innan de beräknade siffrorna exponeras med en begränsad precision (särskilt inom standard JavaScript- eller ECMAScript - gränssnittsbindningar ) .

Andra avrundningsnormer

Vissa discipliner eller institutioner har utfärdat standarder eller direktiv för avrundning.

amerikanska väderobservationer

I en riktlinje som utfärdades i mitten av 1966, bestämde US Office of the Federal Coordinator for Meteorology att väderdata skulle avrundas till närmaste runda nummer, med "runda hälften uppåt"-regeln. Till exempel ska 1,5 avrundat till heltal bli 2 och −1,5 ska bli −1. Före det datumet var den oavgjorda regeln "runda hälften bort från noll".

Negativ noll i meteorologi

Vissa meteorologer kan skriva "−0" för att indikera en temperatur mellan 0,0 och -0,5 grader (exklusivt) som avrundades till ett heltal. Denna notation används när det negativa tecknet anses viktigt, oavsett hur liten storleken är; till exempel vid avrundning av temperaturer i Celsiusskalan , där under noll indikerar frysning. ^{[ citat behövs ]}

Se även

Kontantavrundning , som hanterar frånvaron av mynt med extremt lågt värde
Data binning , en liknande operation
Gals exakta tabeller
Intervallaritmetik
ISO/IEC 80000
Kahan summeringsalgoritm
Partilista proportionell representation , en tillämpning av avrundning till heltal som har undersökts noggrant
Signerad siffra representation
Avkortning

Anteckningar

externa länkar

Weisstein, Eric W. "Rundning" . MathWorld .
En introduktion till olika avrundningsalgoritmer som är tillgänglig för en allmän publik men särskilt användbar för dig som studerar datavetenskap och elektronik.
Hur man implementerar anpassade avrundningsprocedurer av Microsoft (trasig)