1 + 1 + 1 + 1 + ⋯

Serien 1 + 1 + 1 + 1 + ⋯

Efter utjämning

Asymptotiskt beteende av utjämningen. Linjens y - 1/2 . avsnitt är −

I matematik , 1 + 1 + 1 + 1 + ⋯ , även skrivet $\sum _{n=1}^{\infty }n^{0}$ , $\sum _{n=1}^{\infty }1^{n}$ , eller helt enkelt $\sum _{n=1}^{\infty }1$ , är en divergerande serie , vilket betyder att dess sekvens av delsummor inte konvergerar till en gräns i de reella talen . Sekvensen 1 ⁿ kan ses som en geometrisk serie med det gemensamma förhållandet 1. Till skillnad från andra geometriska serier med rationellt förhållande (förutom −1 ), konvergerar den varken i de reella talen eller i de p -adiska talen för vissa p . I samband med den utökade reella tallinjen

$\sum _{n=1}^{\infty }1=+\infty \,,$

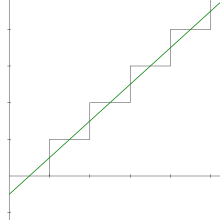
eftersom dess sekvens av delsummor ökar monotont utan begränsning.

Där summan av n ⁰ förekommer i fysiska tillämpningar, kan det ibland tolkas av zetafunktionsregularisering , som värdet vid s = 0 för Riemanns zetafunktion :

$\zeta (s)=\sum _{n=1}^{\infty }{\frac {1}{n^{s}}}={\frac {1}{1-2^{1 -s}}}\summa _{n=1}^{\infty }{\frac {(-1)^{n+1}}{n^{s}}}\,.$

De två formlerna ovan är dock inte giltiga vid noll, men den analytiska fortsättningen är det.

$\zeta (s)=2^{s}\pi ^{s -1}\ \sin \left({\frac {\pi s}{2}}\höger)\ \Gamma (1-s)\ \zeta (1-s)\!,$

Genom att använda denna får man (med tanke på att Γ(1) = 1 ),

$\zeta (0)={\frac {1}{\pi }}\lim _{s\rightarrow 0}\ \sin \left({\frac {\pi s}{ 2}}\right)\ \zeta (1-s)={\frac {1}{\pi }}\lim _{s\rightarrow 0}\ \left({\frac {\pi s}{2} }-{\frac {\pi ^{3}s^{3}}{48}}+...\right)\ \left(-{\frac {1}{s}}+...\right )=-{\frac {1}{2}}$

där effektserieexpansionen för ζ ( s ) om s = 1 följer eftersom ζ ( s ) har en enkel pol av rest ett där. I denna mening 1 + 1 + 1 + 1 + ⋯ = ζ (0) = − 1 / 2 .

Emilio Elizalde presenterar en kommentar från andra om serien:

höll två framstående fysiker, A. Slavnov och F. Yndurain , seminarier i Barcelona om olika ämnen. Det var anmärkningsvärt att i båda presentationerna vid något tillfälle talade talaren till publiken med dessa ord: 'Som alla vet, 1 + 1 + 1 + ⋯ = − 1 / 2 .' Antyder kanske: Om du inte vet detta är det ingen idé att fortsätta lyssna.

Se även

• Grandis serie
• 1 − 2 + 3 − 4 + · · ·
• 1 + 2 + 3 + 4 + · · ·
• 1 + 2 + 4 + 8 + · · ·
• 1 − 2 + 4 − 8 + ⋯
• 1 − 1 + 2 − 6 + 24 − 120 + · · ·
• Harmonisk serie

externa länkar

• OEIS -sekvens A000012 (Den enklaste sekvensen av positiva tal: sekvensen av alla 1)