Mekanism design

Stanley Reiter-diagrammet ovan illustrerar ett spel med mekanismdesign. Det övre vänstra utrymmet $\Theta$ visar typutrymmet och det övre högra utrymmet X utrymmet för resultat. Den sociala valfunktionen f $\displaystyle f(\theta )}$ mappar en typprofil till ett utfall. I spel med mekanismdesign skickar agenter meddelanden $M$ i en spelmiljö $g$ . Jämvikten i spelet $\xi (M,g,\theta )$ kan utformas för att implementera någon social valfunktion $f(\theta )$ .

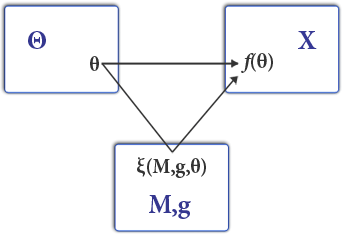
Mekanismdesign är ett fält inom ekonomi och spelteori som tar ett mål-först tillvägagångssätt för att utforma ekonomiska mekanismer eller incitament, mot önskade mål, i strategiska miljöer, där spelarna agerar rationellt. Eftersom det börjar i slutet av spelet och sedan går baklänges, kallas det också omvänd spelteori . Det har breda tillämpningar, från ekonomi och politik inom områden som marknadsdesign , auktionsteori och sociala valteori till nätverkssystem (internet-interdomänrouting, sponsrade sökauktioner).

Mekanismdesign studerar lösningskoncept för en klass av privatinformationsspel. Leonid Hurwicz förklarar att "i ett designproblem är målfunktionen den huvudsakliga "givna", medan mekanismen är det okända. Därför är designproblemet det "inversa" av traditionell ekonomisk teori, som vanligtvis ägnas åt analys av prestandan hos en given mekanism.' Så två utmärkande egenskaper hos dessa spel är:

• att en spel "designer" väljer spelstrukturen snarare än att ärva en
• att designern är intresserad av spelets resultat

2007 års Nobels minnespris i ekonomisk vetenskap tilldelades Leonid Hurwicz , Eric Maskin och Roger Myerson "för att ha lagt grunden till teorin om mekanismdesign".

Intuition

I en intressant klass av bayesianska spel , skulle en spelare, kallad "rektor", vilja villkora sitt beteende på information som andra spelare känner till privat. Till exempel skulle rektorn vilja veta den verkliga kvaliteten på en begagnad bil som en säljare säljer. Han kan inte lära sig någonting bara genom att fråga försäljaren, eftersom det ligger i säljarens intresse att förvränga sanningen. Men i mekanismdesign har rektorn en fördel: Han kan designa ett spel vars regler kan påverka andra att agera som han vill.

Utan mekanismdesignteori skulle rektors problem vara svårt att lösa. Han skulle behöva överväga alla möjliga spel och välja det som bäst påverkar andra spelares taktik. Dessutom skulle huvudmannen behöva dra slutsatser från agenter som kan ljuga för honom. Tack vare mekanismdesign, och särskilt avslöjningsprincipen , behöver rektorn bara överväga spel där agenter sanningsenligt rapporterar sin privata information.

Grunder

Mekanism

Ett spel med mekanismdesign är ett spel med privat information där en av agenterna, kallad huvudmannen, väljer utbetalningsstrukturen. Efter Harsanyi ( 1967 ) får agenterna hemliga "meddelanden" från naturen som innehåller information som är relevant för utbetalningar. Ett meddelande kan till exempel innehålla information om deras preferenser eller kvaliteten på en vara till salu. Vi kallar denna information för agentens "typ" (noteras vanligtvis $\theta$ och följaktligen utrymmet för typerna $\Theta$ ). Agenter rapporterar sedan en typ till rektor (vanligtvis noterad med en hatt ${\hat {\theta }}$ ) som kan vara en strategisk lögn. Efter rapporten betalas huvudmannen och ombuden enligt den utdelningsstruktur som huvudmannen valt.

Tidpunkten för spelet är:

1. Huvudmannen förbinder sig till en mekanism $y()$ som ger ett utfall $y$ som en funktion av rapporterad typ
2. Agenterna rapporterar, möjligen oärligt, en typprofil ${\hat {\theta }}$
3. Mekanismen exekveras (agenter får utfallet $y({\hat {\theta }})$ )

För att förstå vem som får vad är det vanligt att dela upp utfallet $y$ i en varufördelning och en pengaöverföring, ${\displaystyle y(\theta )=\{x(\theta ),t(\theta )\},\ x\in X,t\in T} där x {\displaystyle x$ } $för$ en allokering av varor som utförts eller tagits emot som funktion av typ, och $t$ står för en monetär överföring som funktion av typ.

Som riktmärke definierar designern ofta vad som skulle hända under fullständig information. Definiera en social valfunktion $f(\theta )$ som mappar den (sanna) typprofilen direkt till allokeringen av mottagna eller renderade varor,

$f(\theta ):\Theta \rightarrow X$

Däremot mappar en mekanism den rapporterade typprofilen till ett resultat (igen, både en varuallokering $x$ och en pengaöverföring $t$ )

$y({\hat {\theta }}):\Theta \rightarrow Y$

Uppenbarelseprincipen

Huvudartikel: Uppenbarelseprincipen

En föreslagen mekanism utgör ett Bayesianskt spel (ett spel med privat information), och om det sköter sig väl har spelet en Bayesiansk Nash-jämvikt . Vid jämvikt väljer agenter sina rapporter strategiskt som en funktion av typ

${\hat {\theta }}(\theta )$

Det är svårt att lösa för Bayesiansk jämvikt i en sådan miljö eftersom det innebär att lösa för agenters strategier för bästa svar och för bästa slutledning från en möjlig strategisk lögn. Tack vare ett svepande resultat som kallas uppenbarelseprincipen, oavsett vilken mekanism en designer kan begränsa uppmärksamheten till jämvikter där agenter sanningsenligt rapporterar typ. Uppenbarelseprincipen säger: "Till varje Bayesiansk Nash-jämvikt motsvarar ett Bayesianskt spel med samma jämviktsresultat men där spelare sanningsenligt rapporterar typ. "

Detta är extremt användbart. Principen gör det möjligt för en att lösa en Bayesiansk jämvikt genom att anta att alla spelare är sanningsenligt rapporterade (med förbehåll för en incitamentkompatibilitetsbegränsning) . I ett slag eliminerar det behovet av att överväga antingen strategiskt beteende eller lögn.

Dess bevis är ganska direkt. Antag ett Bayesianskt spel där agentens strategi och utdelning är funktioner av dess typ och vad andra gör, $u_{i} \left(s_{i}(\theta _{i}),s_{-i}(\theta _{-i}),\theta _{i}\right)$ . Per definition är agent i: s jämviktsstrategi $s(\theta _{i})$ Nash i förväntad nytta:

$_ displaystyle s_{i}(\theta _{i})\in \arg \max _{s'_{i}\in S_{i}}\summa _{\theta _{-i}}\ p(\ theta _{-i}\mid \theta _{i})\ u_{i}\left(s'_{i},s_{-i}(\theta _{-i}),\theta _{i }\höger)}$

Definiera helt enkelt en mekanism som skulle få agenter att välja samma jämvikt. Det enklaste att definiera är att mekanismen förbinder sig att spela agenternas jämviktsstrategier för dem.

$y({\hat {\theta }}):\Theta \rightarrow S(\Theta )\rightarrow Y$

Under en sådan mekanism finner agenterna det givetvis optimalt att avslöja typ eftersom mekanismen spelar de strategier som de fann optimala ändå. Formellt, välj $y(\theta )$ så att

${\begin{aligned}\theta _{i}\in {}&\arg \max _{\theta '_{i}\in \Theta }\sum _{\theta _{-i}}\ p(\theta _{-i}\mid \theta _{i})\ u_{i} \left(y(\theta '_{i},\theta _{-i}),\theta _{i}\right)\\[5pt]&=\summa _{\theta _{-i}} \ p(\theta _{-i}\mid \theta _{i})\ u_{i}\left(s_{i}(\theta ),s_{-i}(\theta _{-i}) ,\theta _{i}\right)\end{aligned}}$

Implementerbarhet

Konstruktören av en mekanism hoppas i allmänhet heller

• att designa en mekanism $y()$ som "implementerar" en social valfunktion
• för att hitta mekanismen $y()$ som maximerar något värdekriterium (t.ex. vinst)

Att implementera en social valfunktion $f(\theta )$ är att hitta någon $t(\theta )$ överföringsfunktion som motiverar agenter att välja $f(\theta )$ . Formellt, om jämviktsstrategiprofilen under mekanismen kartläggs till samma varuallokering som en social valfunktion,

$f(\theta )=x\left({\hat {\theta }}(\theta )\right)$

vi säger att mekanismen implementerar den sociala valfunktionen.

Tack vare uppenbarelseprincipen kan designern vanligtvis hitta en överföringsfunktion $t(\theta )$ för att implementera ett socialt val genom att lösa ett tillhörande sanningsberättarspel. Om agenter tycker att det är optimalt att sanningsenligt rapportera typ,

${\hat {\theta }}(\theta )=\theta$

vi säger att en sådan mekanism är sanningsenligt implementerbar (eller bara "implementerbar"). Uppgiften är sedan att lösa ett sanningsenligt implementerbart $t(\theta )$ och tillskriva denna överföringsfunktion till det ursprungliga spelet. En allokering $x(\theta )$ är sanningsenligt implementerbar om det finns en överföringsfunktion $t(\theta )$ så att

$u(x(\theta ),t (\theta ),\theta )\geq u(x({\hat {\theta }}),t({\hat {\theta }}),\theta )\ \forall \theta ,{\hat {\ theta }}\in \Theta$

som också kallas begränsningen för incitamentkompatibilitet (IC).

I applikationer är IC-villkoret nyckeln till att beskriva formen av $t(\theta )$ på något användbart sätt. Under vissa förhållanden kan den till och med isolera överföringsfunktionen analytiskt. läggs ibland ett deltagande ( individuell rationalitet ) till om agenter har möjlighet att inte spela.

Nödvändighet

Tänk på en inställning där alla agenter har en typkontingent hjälpfunktion $u(x,t,\theta )$ . Betrakta också en godsallokering $x(\theta )$ som är vektorvärderad och storleken $k$ (som tillåter $k$ antal varor) och anta att den är styckvis kontinuerlig med hänsyn till dess argument.

Funktionen $x(\theta )$ är implementerbar endast om

$\sum _{k=1}^{n}{\frac {\partial } {\partial \theta }}\left({\frac {\partial u/\partial x_{k}}{\left|\partial u/\partial t\right|}}\right){\frac {\partial x}{\partial \theta }}\geq 0$

närhelst $x=x(\theta )$ och $t=t(\theta )$ och x är kontinuerlig vid $\theta$ . Detta är ett nödvändigt villkor och härleds från första och andra ordningens villkor för agentens optimeringsproblem under antagande om sanningssägande.

Dess betydelse kan förstås i två delar. Den första delen säger att agentens marginella substitutionsgrad (MRS) ökar som en funktion av typen,

${\frac {\partial }{\partial \theta }}\left({\ frac {\partial u/\partial x_{k}}{\left|\partial u/\partial t\right|}}\right)={\frac {\partial }{\partial \theta }}\mathrm { MRS} _{x,t}$

Kort sagt, agenter kommer inte att berätta sanningen om mekanismen inte erbjuder högre agenttyper en bättre affär. Annars kommer högre typer som möter någon mekanism som straffar höga typer för rapportering att ljuga och förklara att de är lägre typer, vilket bryter mot den sanningsberättande IC-begränsningen. Det andra stycket är ett monotoniskt tillstånd som väntar på att hända,

${\frac {\partial x}{\partial \theta }}$

vilket, för att vara positivt, innebär att högre typer måste ges mer av det goda.

Det finns potential för de två delarna att interagera. Om kontraktet för något typområde erbjöd mindre kvantitet till högre typer ${\displaystyle \partial x/\partial \theta <0} ,$ är det möjligt att mekanismen skulle kunna kompensera genom att ge högre typer en rabatt. Men ett sådant kontrakt finns redan för medel av låg typ, så denna lösning är patologisk. En sådan lösning uppstår ibland i processen att lösa en mekanism. I dessa fall måste den " strykas ". I en miljö med flera bra är det också möjligt för designern att belöna agenten med mer av en vara för att ersätta mindre av en annan (t.ex. smör mot margarin ). Flera-goda mekanismer är ett pågående problem inom mekanismdesignteorin.

Tillräcklighet

Mekanismdesignpapper gör vanligtvis två antaganden för att säkerställa implementerbarhet:

1. ${\frac {\partial }{\partial \theta }}{\frac {\partial u/\partial x_{k}}{\left|\partial u/\partial t\right|} }>0\ \forall k$

Detta är känt under flera namn: enkelkorsningsvillkoret , sorteringsvillkoret och Spence–Mirrlees-villkoret. Det betyder att hjälpfunktionen har en sådan form att agentens MRS ökar i typ.

2. $\exists K_{0},K_{1}{\text{ så att }}\left|{\frac {\partial u/\partial x_{k}}{\partial u/\partial t}} \right|\leq K_{0}+K_{1}|t|$

Detta är ett tekniskt tillstånd som begränsar tillväxttakten för MRS.

Dessa antaganden är tillräckliga för att tillhandahålla att varje monoton $x(\theta )$ är implementerbar (en $t(\theta )$ finns som kan implementera den). Dessutom, i singel-bra-inställningen är enkelkorsningsvillkoret tillräckligt för att tillhandahålla att endast ett monotont $x(\theta )$ är implementerbart, så att designern kan begränsa sin sökning till ett monotont $x(\theta )$ .

Markerade resultat

Intäktsekvivalenssats

Huvudartikel: Intäktsekvivalens

Vickrey ( 1961 ) ger ett hyllat resultat att varje medlem i en stor klass av auktioner försäkrar säljaren om samma förväntade intäkt och att den förväntade intäkten är det bästa säljaren kan göra. Detta är fallet om

1. Köparna har identiska värderingsfunktioner (vilket kan vara en funktion av typ)
2. Köparnas typer är oberoende fördelade
3. Köpartyperna hämtas från en kontinuerlig distribution
4. Typfördelningen bär den monotona riskhastighetsegenskapen
5. Mekanismen säljer varan till köparen med den högsta värderingen

Det sista villkoret är avgörande för satsen. En implikation är att för att säljaren ska uppnå högre intäkter måste han chansa på att ge varan till en agent med lägre värdering. Vanligtvis innebär detta att han måste riskera att inte sälja föremålet alls.

Vickrey–Clarke–Groves mekanismer

Huvudartikel: Vickrey–Clarke–Groves-mekanism

Auktionsmodellen Vickrey (1961) utökades senare av Clarke ( 1971 ) och Groves för att behandla ett offentligt val där kostnaden för ett offentligt projekt bärs av alla agenter, t.ex. om man ska bygga en kommunal bro. Den resulterande "Vickrey–Clarke–Groves"-mekanismen kan motivera agenter att välja en socialt effektiv allokering av allmännyttan även om agenter har privata kända värderingar. Med andra ord kan det lösa " allmänningens tragedi " - under vissa förhållanden, i synnerhet kvasilinjär nytta eller om budgetbalans inte krävs.

Tänk på en inställning där $I$ antal agenter har kvasilinjär nytta med privata värderingar $v(x,t,\theta )$ där valutan $t$ värderas linjärt. VCG-designern designar en incitamentskompatibel (därav sanningsenligt implementerbar) mekanism för att erhålla den sanna typens profil, från vilken designern implementerar den socialt optimala allokeringen

$x_{I}^{*}(\theta )\in {\underset {x\in X}{\ operatornamn {argmax} }}\sum _{i\in I}v(x,\theta _{i})$

Det smarta med VCG-mekanismen är hur den motiverar sanningsenlig uppenbarelse. Det eliminerar incitament att felrapportera genom att bestraffa en agent med kostnaden för den snedvridning han orsakar. Bland rapporterna som agenten kan göra tillåter VCG-mekanismen en "noll"-rapport som säger att han är likgiltig för allmännyttan och bara bryr sig om pengaöverföringen. Detta tar effektivt bort agenten från spelet. Om en agent väljer att rapportera en typ, debiterar VCG-mekanismen agenten en avgift om hans rapport är avgörande , det vill säga om hans rapport ändrar den optimala allokeringen x för att skada andra agenter. Betalningen är beräknad

$t_{i}({\hat {\theta }})=\summa _{j\in Ii}v_{j}(x_{Ii}^{*}(\theta _ {Ii}),\theta _{j})-\sum _{j\in Ii}v_{j}(x_{I}^{*}({\hat {\theta}}_{i},\ theta _{I}),\theta _{j})$

som summerar förvrängningen i de andra agenternas (och inte hans egna) verktyg som orsakas av att en agent rapporterar.

Gibbard–Satterthwaites sats

Huvudartikel: Gibbard–Satterthwaite teorem

Gibbard ( 1973 ) och Satterthwaite ( 1975 ) ger ett omöjlighetsresultat som till sin anda liknar Arrows omöjlighetsteorem . För en mycket allmän klass av spel kan endast "diktatoriska" sociala valfunktioner implementeras.

En social valfunktion f () är diktatorisk om en agent alltid får sin mest gynnade varutilldelning,

${\text{för }}f(\Theta ) {\text{, }}\exists i\in I{\text{ så att }}u_{i}(x,\theta _{i})\geq u_{i}(x',\theta _{i })\ \forall x'\in X$

Teoremet säger att under allmänna förhållanden måste alla sanningsenligt implementerbara sociala valfunktioner vara diktatoriska om,

1. X är ändlig och innehåller minst tre element
2. Preferenser är rationella
3. $f(\Theta )=X$

Myerson–Satterthwaites sats

Huvudartikel: Myerson–Satterthwaite teorem

Myerson och Satterthwaite ( 1983 ) visar att det inte finns något effektivt sätt för två parter att handla med en vara när de var och en har hemliga och sannolikt varierande värderingar för den, utan risken att tvinga en part att handla med förlust. Det är bland de mest anmärkningsvärda negativa resultaten inom ekonomi – en sorts negativ spegel av välfärdsekonomins grundläggande satser .

Shapley värde

Huvudartikel: Shapley-värde

Phillips och Marden (2018) bevisade att för kostnadsdelningsspel med konkava kostnadsfunktioner, den optimala kostnadsdelningsregeln som för det första optimerar de värsta ineffektiviteterna i ett spel (priset för anarki), och sedan för det andra optimerar det bästa fallet utfall ( priset för stabilitet ), är just Shapley-regeln om kostnadsdelning. Ett symmetriskt uttalande är på samma sätt giltigt för spel som delar verktyg med konvexa verktygsfunktioner.

Exempel

Pris diskriminering

Mirrlees ( 1971 ) introducerar en inställning där överföringsfunktionen t () är lätt att lösa. På grund av dess relevans och lätthanterlighet är det en vanlig miljö i litteraturen. Tänk på en enkel-bra, singelagent-inställning där agenten har kvasilinjär nytta med en okänd typparameter $\theta$

$u(x,t,\theta )=V(x,\theta )-t$

och där huvudmannen har en tidigare CDF över agentens typ $P(\theta )$ . Huvudmannen kan producera varor till en konvex marginalkostnad c ( x ) och vill maximera den förväntade vinsten från transaktionen

$\max _{x(\theta ),t(\theta )}\mathbb {E} _{\theta }\left[t(\theta )-c\left(x(\theta )\right)\right]$

beroende av IC- och IR-villkor

$u(x(\theta ),t(\ theta ),\theta )\geq u(x(\theta '),t(\theta '),\theta )\ \forall \theta ,\theta '$

$u(x(\theta ),t(\theta ),\theta )\geq {\underline {u}}(\theta )\ \forall \theta$

Huvudmannen här är en monopolist som försöker fastställa ett vinstmaximerande prisschema där den inte kan identifiera typen av kund. Ett vanligt exempel är ett flygbolag som sätter priser för affärs-, fritids- och studentresenärer. På grund av IR-tillståndet måste det ge varje typ en tillräckligt bra affär för att framkalla deltagande. På grund av IC-tillståndet måste den ge varje typ en tillräckligt bra affär för att typen föredrar sin affär framför alla andra.

Ett knep som ges av Mirrlees (1971) är att använda kuvertsatsen för att eliminera överföringsfunktionen från förväntan att maximeras,

${\text{let }}U(\theta )=\max _{\theta '}u \left(x(\theta '),t(\theta '),\theta \right)$

${\frac {dU}{d\theta }}={\frac {\partial u}{\partial \theta }}={\frac {\partial V}{\partial \theta }}$

Integrering,

$U(\theta )={\understryka {u}}(\theta _{0})+\int _ {\theta _{0}}^{\theta }{\frac {\partial V}{\partial {\tilde {\theta }}}}d{\tilde {\theta }}$

där $\theta _{0}$ är någon indextyp. Ersätter det incitamentskompatibla $t(\theta )=V(x(\theta ),\theta )-U(\theta )$ i maximanden,

${\begin{aligned}&\mathbb {E} _{\ theta }\left[V(x(\theta ),\theta )-{\underline {u}}(\theta _{0})-\int _{\theta _{0}}^{\theta }{ \frac {\partial V}{\partial {\tilde {\theta }}}}d{\tilde {\theta }}-c\left(x(\theta)\right)\right]\\&{} =\mathbb {E} _{\theta }\left[V(x(\theta),\theta )-{\underline {u}}(\theta _{0})-{\frac {1-P( \theta )}{p(\theta )}}{\frac {\partial V}{\partial \theta }}-c\left(x(\theta )\right)\right]\end{aligned}}$

efter en integrering av delar. Denna funktion kan maximeras punktvis.

Eftersom $U(\theta )$ är incitamentskompatibel redan kan designern släppa IC-begränsningen. Om verktygsfunktionen uppfyller Spence–Mirrlees-villkoret finns en monoton ${\displaystyle x(\theta )}-$ funktion. IR-begränsningen kan kontrolleras vid jämvikt och avgiftsschemat kan höjas eller sänkas i enlighet med detta. Notera dessutom förekomsten av en riskfrekvens i uttrycket. Om typfördelningen bär den monotona riskkvotsegenskapen är FOC tillräcklig för att lösa för t (). Om inte, då är det nödvändigt att kontrollera om monotonisitetsbegränsningen (se tillräcklighet ovan) är uppfylld överallt längs allokerings- och avgiftsplanerna. Om inte, måste designern använda Myerson-strykning.

Myerson stryker

Det är möjligt att lösa ett varu- eller prisschema som uppfyller villkoren för första beställning men som inte är monotont. Om så är fallet är det nödvändigt att "stryka" schemat genom att välja något värde för att platta till funktionen.

I vissa applikationer kan konstruktören lösa första ordningens villkor för pris- och allokeringsscheman men ändå upptäcka att de inte är monotona. Till exempel, i den kvasilinjära miljön händer detta ofta när riskkvoten i sig inte är monoton. Enligt Spence–Mirrlees villkor måste de optimala pris- och allokeringsscheman vara monotona, så designern måste eliminera alla intervall över vilket schemat ändrar riktning genom att platta till det.

Intuitivt, vad som händer är att designern tycker att det är optimalt att slå ihop vissa typer och ge dem samma kontrakt. Normalt motiverar designern högre typer att utmärka sig genom att ge dem en bättre affär. Om det inte finns tillräckligt få högre typer i marginalen anser konstruktören att det inte lönar sig att ge lägre typer en koncession (kallad deras informationshyra) för att debitera högre typer ett typspecifikt kontrakt.

Överväg att en monopolistisk huvudman säljer till agenter med kvasilinjär nytta, exemplet ovan. Antag att allokeringsschemat $x(\theta )$ som uppfyller första ordningens villkor har en enda inre topp vid $\theta _{1}$ och ett enda inre dal vid ${\displaystyle \theta _{2}>\theta _{1}} ,$ illustrerad till höger.

• Efter Myerson (1981) platta till det genom att välja $x$ som uppfyller
  $$\int _{\phi _{2}(x)}^{\phi _{1}(x)}\left({\frac {\partial V}{\partial x }}(x,\theta )-{\frac {1-P(\theta )}{p(\theta )}}{\frac {\partial ^{2}V}{\partial \theta \,\partial x}}(x,\theta )-{\frac {\partial c}{\partial x}}(x)\right)d\theta =0$$
  där $\phi _{1}(x)$ är den inversa funktionen av x avbildning till $\theta \leq \theta _{1}$ och $\phi _{2}(x)$ är den inversa funktionen av x avbildning till $\theta \geq \theta _{2}$ . Det vill säga, $\phi _{1}$ returnerar ett $\theta$ före den inre toppen och $\phi _{2}$ returnerar ett $\theta$ efter det inre tråget.
• Om det icke-monotona området för $x(\theta )$ gränsar till kanten av typrymden, ställ helt enkelt in lämplig ${\displaystyle \phi (x)}-$ funktion (eller båda) till gränstyp. Om det finns flera regioner, se en lärobok för en iterativ procedur; det kan vara så att mer än ett tråg ska strykas tillsammans.

Bevis

Beviset använder teorin om optimal kontroll. Den tar hänsyn till mängden intervall $\left[{\underline {\theta }},{\overline {\theta }}\right]$ i det icke-monotona området av ${ \displaystyle x(\theta )}$ över vilket det kan platta till schemat. Den skriver sedan en Hamiltonian för att erhålla nödvändiga villkor för en $x(\theta )$ inom intervallen

1. som tillfredsställer monotoni
2. för vilka monotonisitetsbegränsningen inte är bindande för intervallets gränser

Villkor två säkerställer att $x(\theta )$ som uppfyller det optimala kontrollproblemet återansluter till schemat i det ursprungliga problemet vid intervallgränserna (inga hopp). Alla $x(\theta )$ som uppfyller de nödvändiga villkoren måste vara platt eftersom de måste vara monotona och ändå återansluta vid gränserna.

Som tidigare maximera huvudmannens förväntade utdelning, men den här gången med förbehåll för monotonisitetsbegränsningen

${\frac {\partial x}{\partial \theta }}\geq 0$

och använd en Hamiltonian för att göra det, med skuggpris $\nu (\theta )$

$H=\left(V(x,\theta )-{\underline {u}}(\theta _{0})-{\frac {1-P(\theta )}{p (\theta )}}{\frac {\partial V}{\partial \theta }}(x,\theta )-c(x)\right)p(\theta )+\nu (\theta ){\frac {\partial x}{\partial \theta }}$

där $x$ är en tillståndsvariabel och $\partial x/\partial \theta$ kontrollen. Som vanligt vid optimal kontroll måste ekvationen för costate-evolutionen uppfyllas

${\frac {\partial \nu }{\partial \theta }}=-{\frac {\partial H}{\partial x}}=-\left({\ frac {\partial V}{\partial x}}(x,\theta )-{\frac {1-P(\theta )}{p(\theta )}}{\frac {\partial ^{2}V }{\partial \theta \,\partial x}}(x,\theta )-{\frac {\partial c}{\partial x}}(x)\right)p(\theta )$

Genom att dra nytta av villkor 2, notera att monotonisitetsbegränsningen inte är bindande vid gränserna för $\theta$ -intervallet,

$\nu ({\underline {\theta }})=\nu ({\overline {\theta }})=0$

vilket innebär att costate-variabelvillkoret kan integreras och också är lika med 0

$\int _{\underline {\theta }}^{\overline {\theta }}\left({\frac {\partial V}{\partial x}}(x,\theta) -{\frac {1-P(\theta )}{p(\theta )}}{\frac {\partial ^{2}V}{\partial \theta \,\partial x}}(x,\theta )-{\frac {\partial c}{\partial x}}(x)\right)p(\theta )\,d\theta =0$

Den genomsnittliga förvrängningen av huvudmannens överskott måste vara 0. För att platta till schemat, hitta ett $x$ så att dess inversa bild mappas till ett $\theta$ -intervall som uppfyller villkoret ovan.

Se även

• Algoritmisk mekanismdesign
• Alvin E. Roth – Nobelpris, marknadsdesign
• Uppdragsproblem
• Kontraktsteori
• Implementeringsteori
• Incitament kompatibilitet
• Uppenbarelseprincipen
• Smart marknad
• Metagame

Anteckningar

•    Clarke, Edward H. (1971). "Multipart Pricing of Public Goods" (PDF) . Offentligt val . 11 (1): 17–33. doi : 10.1007/BF01726210 . JSTOR 30022651 . S2CID 154860771 .
•   Gibbard, Allan (1973). "Manipulation av röstningssystem: Ett allmänt resultat" (PDF) . Econometrica . 41 (4): 587–601. doi : 10.2307/1914083 . JSTOR 1914083 .
•   Groves, Theodore (1973). "Incitament i lag" (PDF) . Econometrica . 41 (4): 617–631. doi : 10.2307/1914085 . JSTOR 1914085 .
•   Harsanyi, John C. (1967). "Spel med ofullständig information som spelas av "bayesianska" spelare, I-III. del I. Grundmodellen". Management Science . 14 (3): 159–182. doi : 10.1287/mnsc.14.3.159 . JSTOR 2628393 .
•   Mirrlees, JA (1971). "En utforskning av teorin om optimal inkomstbeskattning" (PDF) . Genomgång av ekonomiska studier . 38 (2): 175–208. doi : 10.2307/2296779 . JSTOR 2296779 . Arkiverad från originalet (PDF) 2017-05-10 . Hämtad 2016-08-12 .
• Myerson, Roger B.; Satterthwaite, Mark A. (1983). "Effektiva mekanismer för bilateral handel" (PDF) . Journal of Economic Theory . 29 (2): 265–281. doi : 10.1016/0022-0531(83)90048-0 . hdl : 10419/220829 .
•   Satterthwaite, Mark Allen (1975). "Strategisäkerhet och Arrows villkor: Existens- och korrespondenssatser för röstningsförfaranden och sociala välfärdsfunktioner". Journal of Economic Theory . 10 (2): 187–217. CiteSeerX 10.1.1.471.9842 . doi : 10.1016/0022-0531(75)90050-2 .
• Vickrey, William (1961). "Motspekulation, auktioner och konkurrenskraftiga slutna anbud" ( PDF) . The Journal of Finance . 16 (1): 8–37. doi : 10.1111/j.1540-6261.1961.tb02789.x .

Vidare läsning

• Kapitel 7 i   Fudenberg, Drew; Tirole, Jean (1991), Game Theory , Boston: MIT Press , ISBN 978-0-262-06141-4 . En standardtext för examen i spelteori.
• Kapitel 23 av   Mas-Colell ; Whinston; Green (1995), Microeconomic Theory , Oxford: Oxford University Press , ISBN 978-0-19-507340-9 . En standardtext för examen i mikroekonomi.
•   Milgrom, Paul (2004), Putting Auction Theory to Work , New York: Cambridge University Press , ISBN 978-0-521-55184-7 . Tillämpningar av principer för mekanismdesign i samband med auktioner.
• Noam Nisan . Ett tekniksamtal från Google om mekanismdesign.
• Legros, Patrick; Cantillon, Estelle (2007). "Vad är mekanismdesign och varför spelar det roll för beslutsfattande?" . Centrum för ekonomisk-politisk forskning .
• Roger B. Myerson (2008). "Mechanism Design," The New Palgrave Dictionary of Economics Online, abstrakt.
•   Diamantaras, Dimitrios (2009), A Toolbox for Economic Design , New York: Palgrave Macmillan , ISBN 978-0-230-61060-6 . En examenstext specifikt fokuserad på mekanismdesign.

externa länkar

• Eric Maskin " Nobelprisföreläsning " hölls den 8 december 2007 på Aula Magna , Stockholms universitet.