Fångens dilemma

För annan användning, se Prisoner's dilemma (disambiguation) .

Ej att förväxla med Three Prisoners-problemet , Oväntad hängande paradox , 100 prisoners-problemet eller Oskyldiga fångars dilemma .

Standard prisoner's dilemma payoff matris

B A	B är tyst	B förråder
A är tyst	−2 −2	0 −10
A förråder	−10 0	−5 −5

Fångens dilemma är ett spel som analyseras i spelteori . Det är ett tankeexperiment som utmanar två helt rationella agenter till ett dilemma: de kan samarbeta med sin partner för ömsesidig nytta eller förråda sin partner ("defekt") för individuell belöning.

Detta dilemma inramades ursprungligen av Merrill Flood och Melvin Dresher 1950 medan de arbetade på RAND . Albert W. Tucker formaliserade senare spelet genom att strukturera belöningarna i form av fängelsestraff och kallade det "fångens dilemma". William Poundstone beskrev spelet i sin bok Prisoner's Dilemma från 1993 :

Två medlemmar av ett kriminellt gäng, A och B, grips och fängslas. Varje fånge är i isoleringscell utan kommunikation med sin partner. Huvudantalet skulle leda till ett straff på tio års fängelse; polisen har dock inte bevis för en fällande dom. De planerar att döma båda till två års fängelse på en mindre anklagelse, men erbjuder varje fånge ett faustiskt fynd : Om en av dem erkänner brottet enligt huvudanklagelsen och förråder den andra, kommer de att bli benådade och fria att lämna medan de andra måste avtjäna hela straffet i stället för bara två år för den mindre avgiften.

Detta leder till en möjlig av fyra olika utfall:

• A: Om A och B båda förblir tysta, kommer de var och en att avtjäna den lägsta anklagelsen om 2 års fängelse.
• B: Om A förråder B men B förblir tyst kommer A att försättas på fri fot medan B avtjänar 10 års fängelse.
• C: Om A förblir tyst men B förråder A, kommer A att avtjäna 10 år i fängelse och B kommer att försättas på fri fot.
• D: Om A och B båda förråder den andra delar de på straffet och avtjänar 5 år.

Som en projektion av rationellt beteende när det gäller lojalitet till sin partner i brott antyder Fångens Dilemma att kriminella som erbjuds en större belöning kommer att förråda sin partner.

Lojalitet mot sin partner är, i detta spel, irrationell. Detta särskilda antagande om rationalitet innebär att det enda möjliga resultatet för två rent rationella fångar är svek, även om ömsesidigt samarbete skulle ge en större nettobelöning. Alternativa idéer som styr beteende har föreslagits — se till exempel Elinor Ostrom .

Den bästa responsen, dvs. den dominerande strategin är att förråda den andre, vilket stämmer överens med den säkra principen . Fångens dilemma illustrerar också att de beslut som fattas under kollektiv rationalitet inte nödvändigtvis är desamma som de som fattas under individuell rationalitet. Denna konflikt är också uppenbar i en situation som kallas " Tragedy of the Commons ".

I verkligheten uppstår systemisk fördom mot samarbetsbeteende trots förutsägelser från enkla modeller av "rationellt" egenintressant agerande. Denna partiskhet mot samarbete har varit uppenbar sedan detta spel först genomfördes på RAND: Inblandade sekreterare litade ofta på varandra och arbetade tillsammans mot det bästa gemensamma resultatet.

Fångens dilemma blev fokus för omfattande experimentell forskning. Denna forskning har tagit en av tre former: enkelspel (agenter spelar bara ett spel), itererat spel (agenter spelar flera spel i följd) och itererat spel mot en programmerad spelare. Forskning om fångens dilemma har tjänat till att rättfärdiga det kategoriska imperativ som Immanuel Kant tog upp , som säger att en rationell agent förväntas "handla på det sätt du vill att andra ska agera". Denna teori är avgörande för en situation som involverar olika spelare som var och en agerar för sitt bästa och som måste ta hänsyn till andras handlingar för att göra sitt eget val.

I den "iterativa" varianten av spelet, där två agenter spelar mot varandra flera gånger, har agenter kontinuerligt möjlighet att straffa den andra för tidigare beslut. Om antalet gånger spelet kommer att spelas är känt för spelarna, kommer två klassiskt rationella spelare genom bakåtinduktion att förråda varandra upprepade gånger, av samma skäl som single-shot-varianten. I ett spel med oändlig eller okänd längd finns det ingen fast optimal strategi, och prisoner's dilemma-turneringar har hållits för att tävla och testa algoritmer för sådana fall.

Den itererade versionen av fångens dilemma är av särskilt intresse för forskare. På grund av dess iterativa karaktär observerade tidigare forskare att frekvensen för spelare att samarbeta kan förändras, baserat på resultaten av varje iteration. Specifikt kan en spelare vara mindre villig att samarbeta om deras motsvarighet inte samarbetade många gånger, vilket leder till besvikelse. Omvänt, allt eftersom tiden går, kan samarbetet öka på grund av inrättandet av en "tyst överenskommelse" mellan spelare. En annan aspekt angående den itererade versionen av experimentet är att denna tysta överenskommelse mellan spelare alltid har etablerats framgångsrikt även när antalet iterationer offentliggörs för båda sidor.

Fångens dilemmaspel kan modellera många verkliga situationer som involverar kooperativt beteende. I tillfälligt bruk kan beteckningen "fångens dilemma" appliceras på alla situationer där två enheter kan få viktiga fördelar av att samarbeta eller lida av underlåtenhet att göra det men finner det svårt eller dyrt – men inte nödvändigtvis omöjligt – att samordna sina aktiviteter .

Strategi för fångens dilemma

Två fångar är separerade i individuella rum och kan inte kommunicera med varandra. Det vanliga spelet visas nedan:

Fånge B Fången A	Fånge B förblir tyst ( samarbetar )	Fånge B förråder ( defekter )
Fånge A förblir tyst ( samarbetar )	Varje tjänstgör 2 år	Fånge A: 10 år Fånge B: går fri
Fånge A förråder ( defekter )	Fånge A: går fri Fånge B: 10 år	Varje tjänstgör 5 år

Det antas att båda fångarna förstår spelets natur, inte har någon lojalitet mot varandra och inte kommer att ha någon möjlighet till vedergällning eller belöning utanför spelet. Oavsett vad den andre bestämmer så får varje fånge en högre belöning genom att förråda den andre ("avhoppa"). Resonemanget går ut på att analysera båda spelarnas bästa svar : B kommer antingen att samarbeta eller defekta. Om B samarbetar borde A hoppa av, för att gå fri är bättre än att avtjäna 2 år. Om B misslyckas, bör A också defekta, eftersom att avtjäna 5 år är bättre än att tjäna 10. Så, i vilket fall som helst, bör A defekta eftersom avvikelse är A:s bästa svar oavsett B:s strategi. Parallellt resonemang kommer att visa att B borde brista.

Avhopp resulterar alltid i en bättre utdelning än samarbete, så det är en strikt dominerande strategi för både A och B. Ömsesidigt avhopp är den enda starka Nash-jämvikten i spelet (dvs. det enda resultatet som varje spelare bara kunde göra sämre genom att ensidigt ändra strategi). Dilemmat är att ömsesidigt samarbete ger ett bättre resultat än ömsesidigt avhopp men är inte det rationella resultatet eftersom valet att samarbeta, ur ett egenintresseperspektiv, är irrationellt. Således är Prisoners dilemma ett spel där Nash-jämvikten inte är Pareto-effektiv .

Generaliserad form

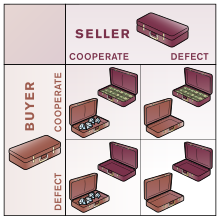
Strukturen i det traditionella fångsdilemmat kan generaliseras från dess ursprungliga fångmiljö. Antag att de två spelarna representeras av färgerna rött och blått och att varje spelare väljer att antingen "samarbeta" eller "defekt".

Om båda spelarna samarbetar får de båda belöningen R för att de samarbetar. Om båda spelarna hoppar av får de båda straffutbetalningen P . Om Blue defektar medan Röd samarbetar, då får Blå frestelsens utdelning T , medan Röd får "sugarens" utdelning, S . På liknande sätt, om Blå samarbetar medan Röd defektar, får Blå Suckers utdelning S , medan Röd får frestelsens utdelning T .

Detta kan uttryckas i normal form :

Kanonisk PD payoff matris

Röd Blå	Samarbeta	Defekt
Samarbeta	R R	T S
Defekt	S T	P P

och för att vara ett fångs dilemmaspel i stark mening måste följande villkor gälla för utdelningen:

$T>R>P>S$

Utdelningsrelationen $R>P$ antyder att ömsesidigt samarbete är överlägset ömsesidigt avhopp, medan payoff-relationerna $T>R$ och $P>S$ antyder att avhopp är den dominerande strategin för båda agenterna.

Specialfall: donationsspel

"Donationsspelet" är en form av fångdilemma där samarbete motsvarar att erbjuda den andra spelaren en förmån b till en personlig kostnad c med b > c . Avhopp innebär att inte erbjuda någonting. Utdelningsmatrisen är alltså

Röd Blå	Samarbeta	Defekt
Samarbeta	b − c b − c	b − c
Defekt	− c b	0 0

Observera att $2R>T+S$ (dvs. $2(bc)>bc$ ), vilket kvalificerar donationsspelet att vara ett itererat spel (se nästa avsnitt).

Donationsspelet kan appliceras på marknader. Antag att X odlar apelsiner och Y odlar äpplen. Ett marginalnytta för apelsinodlaren X är b , vilket är högre än marginalnyttan ( c ) för en apelsin, eftersom X har ett överskott av apelsiner och inga äpplen. På liknande sätt, för äppelodlare Y, är marginalnyttan för en apelsin b medan marginalnyttan för ett äpple är c ​​. Om X och Y kontrakterar att byta ut ett äpple och en apelsin, och var och en fullföljer sitt slut på affären, får var och en en utdelning på b - c . Om man "felar" och inte levererar som utlovat får avhopparen en utdelning på b , medan samarbetspartnern förlorar c . Om båda defekta vinner eller förlorar varken någonting.

Den itererade fångens dilemma

Om två spelare spelar fångens dilemma mer än en gång i följd, minns tidigare handlingar av sin motståndare och tillåts ändra sin strategi i enlighet med detta, kallas spelet det itererade fångsdilemmat.

Utöver det allmänna formuläret ovan kräver den iterativa versionen också att ${\displaystyle 2R>T+S} ,$ för att förhindra att omväxlande samarbete och avhopp ger en större belöning än ömsesidigt samarbete.

Det itererade fångsdilemmaspelet är grundläggande för vissa teorier om mänskligt samarbete och förtroende. Om man antar att spelet effektivt modellerar transaktioner mellan två personer som kräver förtroende, kan samarbetsbeteende i populationer modelleras av en itererad version av spelet för flera spelare. År 1975 Grofman och Pool antalet vetenskapliga artiklar som ägnats åt det till över 2 000. Det upprepade fångsdilemmat kallas också för " fredskrigsspelet" .

Om spelet spelas N gånger och båda spelarna vet detta, är den dominerande strategin att hoppa av i alla omgångar. Den enda möjliga Nash-jämvikten är att alltid defekta. Beviset är induktivt : Man kan lika gärna hoppa av i sista svängen, eftersom motståndaren inte kommer att ha en chans att senare hämnas. Därför kommer båda att defekta på sista svängen. Således kan spelaren lika gärna hoppa av i den näst sista svängen, eftersom motståndaren kommer att hoppa av på den sista oavsett vad som görs, och så vidare. Detsamma gäller om spellängden är okänd men har en känd övre gräns.

Till skillnad från standardfångens dilemma är avhoppningsstrategin i det itererade fångsdilemmat kontraintuitiv och misslyckas med att förutsäga beteendet hos mänskliga spelare, trots att avhopp är det enda korrekta svaret i standardspelteorin. Den superrationella strategin i det itererade fångens dilemma med fast N är att samarbeta mot en superrationell motståndare, och i gränsen för stort N stämmer experimentella resultat på strategier överens med den superrationella versionen snarare än den spelteoretiska rationella.

För att samarbete ska uppstå mellan spelteoretiska rationella spelare måste antalet omgångar N vara okänt för spelarna. I det här fallet kanske "alltid defekt" inte längre är en strikt dominerande strategi utan bara en Nash-jämvikt. Som framgår av Robert Aumann i en tidning upprätthålla det kooperativa resultatet.

Enligt en experimentell studie från 2019 i American Economic Review som testade vilka strategier verkliga försökspersoner använde i upprepade fångars dilemmasituationer med perfekt övervakning, var majoriteten av de valda strategierna alltid att defektera, tit-för-tat och dyster utlösa . Vilken strategi försökspersonerna valde berodde på spelets parametrar.

Strategi för den itererade fångens dilemma

Intresset för iterated prisoner's dilemmat (IPD) väcktes av Robert Axelrod i hans bok The Evolution of Cooperation (1984), där han rapporterar om en turnering som han organiserade av N step prisoner's dilemmat (med N fast) där deltagarna har att välja sin gemensamma strategi om och om igen och ha minne av sina tidigare möten. Axelrod bjöd in akademiska kollegor från hela världen att utforma datorstrategier för att tävla i en IPD-turnering. De program som gick in varierade stort i algoritmisk komplexitet, initial fientlighet, förmåga att förlåta och så vidare.

Axelrod upptäckte att när dessa möten upprepades under en lång tidsperiod med många spelare, var och en med olika strategier, tenderade giriga strategier att fungera mycket dåligt i det långa loppet medan mer altruistiska strategier gjorde det bättre, rent bedömt utifrån egenintresse . Han använde detta för att visa en möjlig mekanism för utvecklingen av altruistiskt beteende från mekanismer som från början är rent själviska, genom naturligt urval .

Den vinnande deterministiska strategin var tit för tat , utvecklad och deltog i turneringen av Anatol Rapoport . Det var det enklaste av alla anmälda program, som bara innehöll fyra rader BASIC , och vann tävlingen. Strategin är helt enkelt att samarbeta på den första iterationen av spelet; efter det gör spelaren vad hans eller hennes motståndare gjorde vid föregående drag. Beroende på situationen kan en lite bättre strategi vara "titt för tat med förlåtelse". När motståndaren defektar, vid nästa drag, samarbetar spelaren ibland ändå, med en liten sannolikhet (runt 1–5%). Detta möjliggör tillfällig återhämtning från att bli instängd i en cykel av avhopp. Den exakta sannolikheten beror på motståndarnas laguppställning.

Efter att ha analyserat strategierna för bästa poäng, angav Axelrod flera villkor som var nödvändiga för att en strategi ska lyckas:

Nice

Den viktigaste förutsättningen är att strategin ska vara "snäll". Det vill säga, den kommer inte att defekta innan dess motståndare gör det (detta kallas ibland för en "optimistisk" algoritm). Nästan alla strategier för bästa poäng var bra. En rent självisk strategi kommer inte att "fuska" sin motståndare av rent egenintresserade skäl först.

Repressalier

Men, hävdade Axelrod, får den framgångsrika strategin inte vara en blind optimist; det måste ibland hämnas. Ett exempel på en strategi utan repressalier är Always Cooperate, ett mycket dåligt val som ofta kommer att utnyttjas av "otäcka" strategier.

Förlåtande

Framgångsrika strategier måste också vara förlåtande. Även om spelare kommer att hämnas, kommer de återigen att falla tillbaka till att samarbeta om motståndaren inte fortsätter att hoppa av. Detta kan stoppa långa serier av hämnd och mothämnd, vilket maximerar poängen.

Icke-avundsjuk

Den sista egenskapen är att vara icke-avundsjuk, vilket betyder att inte sträva efter att göra fler mål än motståndaren.

Den optimala (poängmaximerande) strategin för engångs-PD-spelet är helt enkelt avhopp; som förklarat ovan, är detta sant oavsett sammansättningen av motståndare (kollektivt kallad "befolkning") kan vara. Men i det itererade PD-spelet beror den optimala strategin på strategierna hos troliga motståndare och hur de kommer att reagera på avhopp och samarbeten. Betrakta till exempel en population där alla defekt varje gång, utom en enskild individ som följer strategin tit för tat. Den personen har ett litet underläge på grund av förlusten i första svängen. I en sådan population är den optimala strategin för den individen att hoppa av varje gång. I sin tur, givet en population med en viss procentandel av alltid-avhoppare och resten är tit för tat-spelare, beror den optimala strategin för en individ på procentandelen och på mängden iterationer som spelas.

I strategin som kallas Pavlov, win-stay, lose-switch , inför ett misslyckande att samarbeta, byter spelaren strategi nästa tur. Under vissa omständigheter, slår Pavlov alla andra strategier genom att ge förmånsbehandling till medspelare som använder en liknande strategi.

Att härleda den optimala strategin görs vanligtvis på två sätt:

• Bayesiansk Nash-jämvikt : Om den statistiska fördelningen av motsatta strategier kan bestämmas (t.ex. 50 % tit för tat, 50 % samarbetar alltid) kan en optimal motstrategi härledas analytiskt.
• Monte Carlo -simuleringar av populationer har gjorts, där individer med låga poäng dör, och de med höga poäng reproducerar sig (en genetisk algoritm för att hitta en optimal strategi). Blandningen av algoritmer i den slutliga populationen beror i allmänhet på mixen i den ursprungliga populationen. Införandet av mutation (slumpmässig variation under reproduktion) minskar beroendet av den initiala populationen; empiriska experiment med sådana system tenderar att producera mes för tat-spelare (se till exempel Chess 1988), [ men det finns inga analytiska bevis för att detta alltid kommer att inträffa.

Även om mes för tat anses vara den mest robusta grundläggande strategin, introducerade ett team från Southampton University i England en ny strategi vid 20-årsjubileet iterated prisoner's dilemma-tävlingen, som visade sig vara mer framgångsrik än mes för tat. Denna strategi förlitade sig på samverkan mellan program för att uppnå det högsta antalet poäng för ett enskilt program. Universitetet skickade in 60 program till tävlingen, som var designade för att känna igen varandra genom en serie på fem till tio drag vid starten. När detta erkännande väl gjordes, skulle det ena programmet alltid samarbeta och det andra skulle alltid defekta, vilket garanterade maximalt antal poäng för avhopparen. Om programmet insåg att det spelade en icke-Southampton-spelare, skulle det kontinuerligt defekta i ett försök att minimera poängen för det konkurrerande programmet. Som ett resultat visar resultaten från Prisoners' Dilemma Tournament 2004 University of Southamptons strategier på de tre första platserna (och ett antal positioner mot botten), trots att de har färre vinster och många fler förluster än GRIM-strategin. (I en PD-turnering är syftet med spelet inte att "vinna" matcher – vilket lätt kan uppnås genom frekvent avhopp).

Southampton-strategin drar fördel av det faktum att flera bidrag tillåts i just den här tävlingen och att ett lags prestation mättes av den som gjorde högst poäng (vilket betyder att användningen av självuppoffrande spelare var en form av minmaxing ) . På grund av denna nya regel har den här tävlingen också liten teoretisk betydelse när man analyserar strategier för singelagenter jämfört med Axelrods framstående turnering. Det gav dock en grund för att analysera hur man uppnår samarbetsstrategier i ramverk med flera agenter, särskilt i närvaro av buller. I själva verket, långt innan denna turnering med nya regler spelades, påpekade Dawkins i sin bok The Selfish Gene möjligheten att sådana strategier skulle vinna om flera bidrag var tillåtna, men han anmärkte att Axelrod troligen inte skulle ha tillåtit dem om de hade lämnats in. Den förlitar sig också på att kringgå regler om fångens dilemma genom att det inte finns någon kommunikation tillåten mellan de två spelarna, vilket Southampton-programmen utan tvekan gjorde med sin förprogrammerade "tio move dance" för att känna igen varandra; förstärker hur värdefull kommunikation kan vara för att ändra balansen i spelet.

Även utan underförstådd samverkan mellan programvarustrategier (utnyttjade av Southampton-teamet) är inte alltid tit för tat den absoluta vinnaren av en given turnering; det skulle vara mer exakt att säga att dess långsiktiga resultat över en serie turneringar överträffar sina rivaler. (I vilket fall som helst kan en given strategi anpassas något bättre till tävlingen än mes för tat, men mes för tat är mer robust). Detsamma gäller för mes för tat med förlåtelsevariant, och andra optimala strategier: en viss dag kanske de inte "vinner" mot en specifik blandning av motstrategier. Ett alternativt sätt att uttrycka det är att använda den darwinistiska ESS -simuleringen. I en sådan simulering kommer mes för tat nästan alltid att dominera, även om otäcka strategier kommer att glida in och ut ur populationen eftersom en mes för tat-population är genomtränglig av trevliga strategier utan repressalier, som i sin tur är ett lätt byte för de otäcka. strategier. Richard Dawkins visade att här bildar ingen statisk blandning av strategier en stabil jämvikt, och systemet kommer alltid att pendla mellan gränserna.

Stokastiskt itererade fångens dilemma

I ett stokastiskt itererat fångdilemmaspel specificeras strategier av i termer av "samarbetssannolikheter". I ett möte mellan spelare X och spelare Y specificeras X:s strategi av en uppsättning sannolikheter P att samarbeta med Y. P är en funktion av resultaten av deras tidigare möten eller någon delmängd därav. Om P är en funktion av endast deras senaste n möten, kallas det en "minne-n"-strategi. En minne-1-strategi specificeras sedan av fyra samverkanssannolikheter: $P=\{P_{cc},P_{cd},P_ {dc},P_{dd}\}$ , där $P_{ab}$ är sannolikheten att X kommer att samarbeta i det aktuella mötet givet att det tidigare mötet karakteriserades av (ab). $P_{cd}$ exempel, om det föregående mötet var ett där X samarbetade och Y defekterade, då är sannolikheten att X kommer att samarbeta i det aktuella mötet Om var och en av sannolikheterna är antingen 1 eller 0, kallas strategin deterministisk. Ett exempel på en deterministisk strategi är tit-for-tat-strategin skriven som P ={1,0,1,0}, där X svarar som Y gjorde i föregående möte. En annan är win–stay, lose–switch- strategin skriven som P ={1,0,0,1}, där X svarar som i föregående möte, om det var en "vinst" (dvs. cc eller dc) men ändrar strategi om det var en förlust (dvs cd eller dd). Det har visat sig att det för varje minne-n-strategi finns en motsvarande minne-1-strategi som ger samma statistiska resultat, så att endast minne-1-strategier behöver beaktas.

Om vi ​​definierar P som ovanstående 4-elements strategivektor av X och $Q=\{Q_{cc}, Q_{cd} ,Q_{dc},Q_{dd}\}$ som 4-elements strategivektor för Y , kan en övergångsmatris M definieras för X vars ij :e post är sannolikheten att resultatet av ett särskilt möte mellan X och Y kommer att vara j givet att det föregående mötet var i , där i och j är ett av de fyra utfallsindexen: cc , cd , dc eller dd . $\displaystyle M_{cd,cd}=P_{cd}(1-Q_{dc})}$ från X :s synvinkel, är sannolikheten för att resultatet av det aktuella mötet är $att$ det mötet var lika med . (Indeksen för Q är från Y : s synvinkel: ett cd- utfall för X är ett dc -utfall för Y. ) Enligt dessa definitioner kvalificeras det itererade fångsdilemmat som en stokastisk process och M är en stokastisk matris , vilket tillåter alla teorin om stokastiska processer som ska tillämpas.

Ett resultat av stokastisk teori är att det finns en stationär vektor v för matrisen M så att $v\cdot M=v$ . Utan förlust av generalitet kan det specificeras att v är normaliserat så att summan av dess fyra komponenter är enhet. Den ij: e posten i $M^{n}$ ger sannolikheten att resultatet av ett möte mellan X och Y blir j givet att mötet n föregående steg är i . I gränsen när n närmar sig oändligheten kommer M att konvergera till en matris med fasta värden, vilket ger de långsiktiga sannolikheterna för ett möte som producerar j som kommer att vara oberoende av i . Med andra ord kommer raderna av $M^{\infty }$ att vara identiska, vilket ger de långsiktiga jämviktsresultatssannolikheterna för den itererade fångens dilemma utan att det behöver explicit utvärderas ett stort antal interaktioner. Det kan ses att v är en stationär vektor för $M^{n}$ och särskilt $M^{\infty }$ , så att varje rad av $M^{ \infty }$ kommer att vara lika med v . Således specificerar den stationära vektorn sannolikheterna för jämviktsutfall för X . Definierar $S_{x}=\{R,S,T,P\}$ och $}=\{R,T,S,P\}}$${\displaystyle S_ {$ y som kortsiktiga utdelningsvektorer för {cc,cd,dc,dd}-utfallen (från Xs synvinkel), jämviktsutdelningen för X och Y kan nu anges som $s_{x}=v\cdot S_{x}$ och $s_{y}=v\cdot S_ {y}$ , vilket gör att de två strategierna P och Q kan jämföras för deras långsiktiga utdelning.

Noll-determinant strategier

Relationen mellan nolldeterminant (ZD), samarbetande och avvikande strategier i det itererade fångsdilemmat (IPD) illustreras i ett Venn-diagram . Samarbetsstrategier samarbetar alltid med andra samarbetsstrategier, och avvikande strategier bryter alltid mot andra avvikande strategier. Båda innehåller delmängder av strategier som är robusta under starkt urval, vilket innebär att ingen annan minne-1-strategi väljs för att invadera sådana strategier när de är bosatta i en population. Endast samarbetsstrategier innehåller en delmängd som alltid är robust, vilket innebär att ingen annan minne-1-strategi väljs för att invadera och ersätta sådana strategier, under både starkt och svagt urval . Skärningen mellan ZD och bra samarbetsstrategier är uppsättningen generösa ZD-strategier. Utpressningsstrategier är skärningspunkten mellan ZD och icke-robusta avhoppningsstrategier. Tit-for-tat ligger i skärningspunkten mellan samarbets-, avhoppnings- och ZD-strategier.

År 2012 publicerade William H. Press och Freeman Dyson en ny klass av strategier för de stokastiska itererade fångarnas dilemma som kallas "zero-determinant" (ZD) strategier. De långsiktiga vinsterna för möten mellan X och Y kan uttryckas som determinanten för en matris som är en funktion av de två strategierna och de kortsiktiga utdelningsvektorerna: $s_ {x}=D(P,Q,S_{x})$ och $s_{y}=D(P,Q,S_{y})$ , som inte involverar den stationära vektorn v . Eftersom determinantfunktionen $s_{y}=D(P,Q,f)$ är linjär i f , följer det att $\alpha s_{x}+\beta s_{y}+\gamma =D(P,Q,\alpha S_{x}+ \beta S_{y}+\gamma U)$ (där U = {1, 1, 1, 1} ) . Alla strategier för vilka $D(P,Q,\alpha S_{x}+\beta S_{y}+\gamma U)= 0$ är per definition en ZD-strategi, och de långsiktiga utdelningarna följer relationen $\alpha s_{x}+\beta s_{y}+\gamma =0$ .

Tit-for-tat är en ZD-strategi som är "rättvis" i betydelsen att inte få fördelar över den andra spelaren. Men ZD-utrymmet innehåller också strategier som, i fallet med två spelare, kan tillåta en spelare att ensidigt sätta den andra spelarens poäng eller alternativt tvinga en evolutionär spelare att uppnå en utdelning som är någon procent lägre än hans egen. Den utpressade spelaren kunde hoppa av men skulle därmed skada sig själv genom att få en lägre utdelning. Sålunda förvandlar utpressningslösningar det upprepade fångens dilemma till ett slags ultimatumspel . Specifikt kan X välja en strategi för vilken ${\displaystyle D(P,Q,\beta S_{y}+\gamma U)=0} ,$ ensidigt ställa in $s_{y}$ till ett specifikt värde inom ett visst värdeintervall, oberoende av Y : s strategi, vilket ger X möjlighet att "utpressa" spelare Y (och vice versa). (Det visar sig att om X försöker ställa in $s_{x}$ till ett visst värde, är omfånget av möjligheter mycket mindre, endast bestående av fullständigt samarbete eller fullständigt avhopp.)

En förlängning av IPD är en evolutionär stokastisk IPD, där det relativa överflödet av särskilda strategier tillåts förändras, med mer framgångsrika strategier relativt ökande. Denna process kan åstadkommas genom att mindre framgångsrika spelare imiterar de mer framgångsrika strategierna, eller genom att eliminera mindre framgångsrika spelare från spelet, samtidigt som de mer framgångsrika multipliceras. Det har visat sig att orättvisa ZD-strategier inte är evolutionärt stabila . Nyckelintuitionen är att en evolutionärt stabil strategi inte bara måste kunna invadera en annan befolkning (vilket ockuperande ZD-strategier kan göra) utan måste också prestera bra mot andra spelare av samma typ (vilket ockuperande ZD-spelare klarar sig dåligt eftersom de minskar varandras överskott).

Teori och simuleringar bekräftar att utöver en kritisk populationsstorlek förlorar ZD-utpressning i evolutionär konkurrens mot mer samarbetsstrategier, och som ett resultat ökar den genomsnittliga utdelningen i befolkningen när befolkningen är större. Dessutom finns det vissa fall där utpressare till och med kan katalysera samarbetet genom att hjälpa till att bryta ut ur en konfrontation mellan uniformsavhoppare och växlingsagenter som vinner, stannar, förlorar .

Även om utpressande ZD-strategier inte är stabila i stora populationer, är en annan ZD-klass som kallas "generösa" strategier både stabil och robust. Faktum är att när befolkningen inte är för liten, kan dessa strategier ersätta alla andra ZD-strategier och till och med prestera bra mot ett brett spektrum av generiska strategier för upprepade fångars dilemma, inklusive vinna – stanna, förlora – byta. Detta bevisades specifikt för donationsspelet av Alexander Stewart och Joshua Plotkin 2013. Generösa strategier kommer att samarbeta med andra kooperativa spelare, och inför avhopp förlorar den generösa spelaren mer nytta än sin rival. Generösa strategier är skärningspunkten mellan ZD-strategier och så kallade "bra" strategier, som definierades av Akin (2013) till att vara de för vilka spelaren svarar på tidigare ömsesidigt samarbete med framtida samarbete och delar upp förväntad utdelning lika om han får minst kooperativets förväntade utdelning. Bland bra strategier fungerar den generösa (ZD) delmängden bra när populationen inte är för liten. Om populationen är mycket liten tenderar avhoppsstrategier att dominera.

Kontinuerligt itererade fångens dilemma

Det mesta av arbetet med det itererade fångsdilemmat har fokuserat på det diskreta fallet, där spelarna antingen samarbetar eller defektar, eftersom denna modell är relativt enkel att analysera. Vissa forskare har dock tittat på modeller av det kontinuerliga itererade fångdilemma, där spelarna kan ge ett variabelt bidrag till den andra spelaren. Le och Boyd fann att i sådana situationer är samarbete mycket svårare att utveckla än i det diskreta itererade fångsdilemmat. Den grundläggande intuitionen för detta resultat är okomplicerad: i ett kontinuerligt fångsdilemma, om en befolkning börjar i en icke-samarbetsvillig jämvikt, får spelare som bara är marginellt mer samarbetsvilliga än icke-samarbetsvilliga liten nytta av att blanda sig med varandra . Däremot, i ett diskret fångsdilemma, får tit-for-tat-samarbetspartners ett stort utdelningslyft av att sortera med varandra i en icke-samarbetsvillig jämvikt, i förhållande till icke-samarbetsvilliga. Eftersom naturen utan tvekan erbjuder fler möjligheter till varierande samarbete snarare än en strikt dikotomi av samarbete eller avhopp, kan det kontinuerliga fångsdilemmat hjälpa till att förklara varför verkliga exempel på tit-for-tat-liknande samarbete är extremt sällsynta till sin natur (ex. Hammerstein) även om tit för tat verkar robust i teoretiska modeller.

Framväxten av stabila strategier

Spelare verkar inte kunna koordinera ömsesidigt samarbete, och blir därför ofta låsta i den underlägsna men stabila strategin för avhopp. På detta sätt underlättar itererade rundor utvecklingen av stabila strategier. Itererade rundor producerar ofta nya strategier, som har konsekvenser för komplex social interaktion. En sådan strategi är vinna-håll dig förlora-skift. Den här strategin överträffar en enkel Tit-For-Tat-strategi – det vill säga om du kan komma undan med fusk, upprepa det beteendet. Men om du åker fast, byt.

Det enda problemet med denna tit-for-tat-strategi är att de är sårbara för signalfel. Problemet uppstår när en individ fuskar som vedergällning, men den andra tolkar det som fusk. Som ett resultat av detta fuskar nu den andra individen, och sedan startar den ett gungigt mönster av fusk i en kedjereaktion.

Även utan upprepade spel kan starkt upplyst egenintresse resultera i ett stabilt och effektivt resultat.

Verkliga exempel

Fångmiljön kan tyckas konstruerad, men det finns faktiskt många exempel i mänsklig interaktion såväl som interaktioner i naturen som har samma utdelningsmatris. Fångens dilemma är därför av intresse för samhällsvetenskaper som ekonomi , politik och sociologi , såväl som för biologiska vetenskaper som etologi och evolutionsbiologi . Många naturliga processer har abstraherats till modeller där levande varelser är engagerade i oändliga lekar av fångars dilemma. Denna breda tillämpning av PD ger spelet dess betydande betydelse.

Miljöstudier

I miljöstudier är PD uppenbar i kriser som globala klimatförändringar . Det hävdas koldioxidutsläppen _att alla länder kommer att gynnas av ett stabilt klimat, men varje enskilt land är ofta tveksamt till att minska . Den omedelbara fördelen för ett land av att bibehålla nuvarande beteende uppfattas vara större än den påstådda eventuella fördelen för det landet om alla länders beteende ändrades, vilket förklarar dödläget med klimatförändringarna 2007.

En viktig skillnad mellan klimatförändringspolitik och fångens dilemma är osäkerhet; i vilken utsträckning och takt föroreningar kan förändra klimatet är inte känt. Det dilemmat som regeringar står inför skiljer sig därför från fångens dilemma i och med att resultatet av samarbetet är okänt. Denna skillnad tyder på att stater kommer att samarbeta mycket mindre än i ett verkligt itererat fångdilemma, så att sannolikheten för att undvika en möjlig klimatkatastrof är mycket mindre än den som föreslås av en spelteoretisk analys av situationen med hjälp av ett verkligt itererat fångsdilemma.

Osang och Nandy (2003) ger en teoretisk förklaring med bevis för en regleringsdriven win-win-situation i linje med Michael Porters hypotes, där statlig reglering av konkurrerande företag är betydande.

Djur

Samarbete hos många djur kan förstås som ett exempel på fångens dilemma. Ofta deltar djur i långvariga partnerskap, som mer specifikt kan modelleras som itererade fångars dilemma. Till exempel guppy rovdjur i grupp, och de tros straffa icke-samarbetsvilliga inspektörer.

Vampyrfladdermöss är sociala djur som ägnar sig åt ömsesidigt utbyte av mat. Att tillämpa vinsten från fångens dilemma kan hjälpa till att förklara detta beteende:

• Samarbeta/samarbeta: "Belöning: Jag får blod på mina otursnätter, vilket räddar mig från att svälta. Jag måste ge blod på mina lyckliga nätter, vilket inte kostar mig för mycket."
• Defekt/samarbeta: "Frestelse: Du räddar mitt liv på min dåliga natt. Men då får jag den extra fördelen av att inte behöva betala den lilla kostnaden för att mata dig på min godnatt."
• Samarbeta/Defekt: "Sucker's Payoff: Jag betalar kostnaden för att rädda ditt liv på min goda natt. Men på min dåliga natt matar du mig inte och jag löper en verklig risk att svälta ihjäl."
• Defekt/Defekt: "Straff: Jag behöver inte betala de små kostnaderna för att mata dig på mina goda nätter. Men jag löper en reell risk att svälta på mina dåliga nätter."

Psykologi

Inom beroendeforskning / beteendeekonomi påpekar George Ainslie att missbruk kan gjutas som ett intertemporalt PD -problem mellan missbrukarens nuvarande och framtida jag. I det här fallet betyder avvikelse återfall , och det är lätt att se att att inte avbryta både idag och i framtiden är det överlägset bästa resultatet. Fallet där man avstår idag men återfaller i framtiden är det värsta resultatet – i någon mening har disciplinen och självuppoffringen som är inblandad i att avstå idag "slösats bort" eftersom det framtida återfallet innebär att missbrukaren är precis tillbaka där de började och kommer att måste börja om (vilket är ganska demoraliserande och gör det svårare att börja om). Att återfalla idag och imorgon är ett lite "bättre" resultat, för medan missbrukaren fortfarande är beroende har de inte ansträngt sig för att försöka sluta. Det sista fallet, där man ägnar sig åt det beroendeframkallande beteendet idag samtidigt som man avstår från "i morgon" kommer att vara bekant för alla som har kämpat med ett beroende. Problemet här är att (som i andra PD) det finns en uppenbar fördel med att hoppa av "idag", men imorgon kommer man att möta samma PD, och samma uppenbara fördel kommer att finnas då, vilket i slutändan leder till en oändlig rad avhopp.

John Gottman i sin forskning som beskrivs i "The Science of Trust" definierar goda relationer som de där partners vet att de inte ska gå in i (D,D)-cellen eller åtminstone inte fastna dynamiskt där i en loop. Inom kognitiv neurovetenskap kan snabb hjärnsignalering i samband med bearbetning av olika omgångar indikera val vid nästa omgång. Resultat av ömsesidigt samarbete innebär förändringar i hjärnaktivitet som förutsäger hur snabbt en person kommer att samarbeta in natura vid nästa tillfälle; denna aktivitet kan vara kopplad till grundläggande homeostatiska och motiverande processer, vilket möjligen ökar sannolikheten för att kortväga in i (C,C)-cellen i spelet.

Ekonomi

Fångens dilemma har kallats socialpsykologins E. coli , och det har använts flitigt för att forska i olika ämnen som oligopolistisk konkurrens och kollektiva åtgärder för att producera ett kollektivt nytta.

Reklam nämns ibland som ett verkligt exempel på fångens dilemma. När cigarettreklam var laglig i USA var konkurrerande cigaretttillverkare tvungna att bestämma hur mycket pengar de skulle lägga på reklam. Effektiviteten av företag A:s reklam bestämdes delvis av reklam som utfördes av företag B. Likaså påverkas vinsten från reklam för företag B av reklam som utförs av företag A. Om både företag A och företag B valde att annonsera under en viss period, då förnekar annonsen från varje företag den andras, intäkterna förblir konstanta och kostnaderna ökar på grund av kostnaden för reklam. Båda företagen skulle gynnas av minskad reklam. Men om företag B skulle välja att inte annonsera kan företag A ha stor nytta av att annonsera. Icke desto mindre beror den optimala mängden reklam från ett företag på hur mycket reklam det andra gör. Eftersom den bästa strategin är beroende av vad det andra företaget väljer finns det ingen dominerande strategi, vilket gör den något annorlunda än en fånges dilemma. Resultatet är dock likartat genom att båda företagen skulle ha det bättre om de annonserade mindre än i jämvikten. Ibland uppstår kooperativa beteenden i affärssituationer. Till exempel stödde cigaretttillverkarna lagar som förbjuder cigarettreklam, och förstod att detta skulle minska kostnaderna och öka vinsterna i branschen. Denna analys kommer sannolikt att vara relevant i många andra affärssituationer som involverar reklam.

Utan verkställbara överenskommelser är medlemmar i en kartell också inblandade i ett (flerspelar) fångsdilemma. Att ”samarbeta” innebär vanligtvis att hålla priserna på en i förväg överenskommen miniminivå. "Avhoppa" betyder att sälja under denna miniminivå, omedelbart ta affärer (och vinster) från andra kartellmedlemmar. Antitrustmyndigheter vill att potentiella kartellmedlemmar ska ömsesidigt avvika, vilket säkerställer lägsta möjliga priser för konsumenterna .

Sport

Dopning inom idrotten har nämnts som ett exempel på ett fångsdilemma.

Två tävlande idrottare har möjlighet att använda en olaglig och/eller farlig drog för att öka sin prestation. Om ingen idrottare tar drogen, får ingen av dem en fördel. Om bara en gör det, så får den idrottaren en betydande fördel gentemot sin konkurrent, reducerad av de juridiska och/eller medicinska farorna med att ha tagit drogen. Om båda idrottarna tar drogen upphör dock fördelarna och bara farorna kvarstår, vilket försätter dem båda i en sämre position än om ingen av dem hade använt dopning.

I ett samtal med Ken Griffey Jr. efter MLB- säsongen 1998 uttryckte Barry Bonds sin frustration över andra spelares användning av steroider. Bonds sa: "Jag hade en jävla säsong förra året, och ingen gav ett skit. Ingen. Så mycket som jag har klagat på McGwire och Canseco och hela tjuren med steroider, jag är trött på att slåss mot det. Jag fyller 35 så här. år. Jag har tre eller fyra bra säsonger kvar, och jag vill få betalt. Jag ska bara börja använda några hårda grejer, och förhoppningsvis kommer det inte att skada min kropp. Sedan kommer jag ut ur spel och var färdig med det." Bonds befann sig i fångens dilemma som är dopning i baseboll, känslan av att han måste använda steroider så att hans konkurrenter inte har en så betydande fördel gentemot honom, vilket ger honom en jämn spelplan, även om alla har det sämre än om ingen hade använt steroider alls.

Internationell politik

I teorin om internationella relationer används ofta Fångens Dilemma för att visa varför samarbete misslyckas i situationer när samarbetet mellan stater är kollektivt optimalt men individuellt suboptimalt. Ett klassiskt exempel på säkerhetsdilemmat där en ökning av en stats säkerhet (som att öka dess militära styrka) leder till att andra stater fruktar för sin egen säkerhet (eftersom de inte vet om den säkerhetshöjande staten har för avsikt att använda sin växande militär för offensiv syften). Följaktligen kan säkerhetshöjande åtgärder leda till spänningar, eskalering eller konflikt med en eller flera andra parter, vilket ger ett resultat som ingen part verkligen önskar; ett politiskt exempel på fångens dilemma. Säkerhetsdilemmat är särskilt intensivt i situationer när (1) det är svårt att skilja offensiva vapen från defensiva vapen, och (2) offensiv har fördelen i alla konflikter framför försvar. Militärteknik och geografi påverkar starkt balansen mellan anfall och försvar.

Fångens dilemma har ofta använts av realistiska internationella relationsteoretiker för att visa varför alla stater (oavsett deras interna politik eller bekände ideologi) under internationell anarki kommer att kämpa för att samarbeta med varandra även när alla drar nytta av sådant samarbete.

Kritiker av realism hävdar dock att iteration och utvidgning av framtidens skugga är lösningar på fångens dilemma. När skådespelare spelar fångens dilemma en gång har de incitament att hoppa av, men när de förväntar sig att spela det upprepade gånger har de större incitament att samarbeta.

Multiplayer dilemman

Många verkliga dilemman involverar flera spelare. Även om det är metaforiskt, Hardins tragedi om allmänningen ses som ett exempel på en generalisering av PD:n för flera spelare: Varje bybor gör ett val för personlig vinning eller återhållsamhet. Den kollektiva belöningen för enhälligt (eller till och med frekvent) avhopp är mycket låga vinster (representerar förstörelsen av "allmänheten"). Ett gemensamt dilemma som de flesta kan relatera till är att diska i ett gemensamt hus. Genom att inte diska kan en individ tjäna på att spara sin tid, men om det beteendet antas av varje invånare är den samlade kostnaden inga rena tallrikar för någon.

Allmänheten utnyttjas inte alltid: William Poundstone beskriver i en bok om fångens dilemma en situation i Nya Zeeland där tidningslådor lämnas olåsta. Det är möjligt för människor att ta ett papper utan att betala ( hoppa av ), men väldigt få gör det, och känner att om de inte betalar så gör inte andra det heller, vilket förstör systemet. Efterföljande forskning av Elinor Ostrom , vinnare av Nobels minnespris i ekonomisk vetenskap 2009 , antog att tragedin med allmänningen är alltför förenklad, med det negativa resultatet påverkat av yttre influenser. Utan att komplicera påtryckningar kommunicerar och hanterar grupper det gemensamma sinsemellan för ömsesidig nytta, genom att upprätthålla sociala normer för att bevara resursen och uppnå maximal nytta för gruppen, ett exempel på att åstadkomma det bästa möjliga resultatet för PD.

Relaterade spel

Byte av sluten väska

Fångens dilemma som portföljutbyte

Douglas Hofstadter föreslog en gång att människor ofta tycker att problem som PD-problemet är lättare att förstå när det illustreras i form av ett enkelt spel, eller avvägning. Ett av flera exempel han använde var "closed bag exchange":

Två personer träffas och byter stängda väskor, med förutsättningen att en av dem innehåller pengar och den andra innehåller ett köp. Endera spelare kan välja att hedra affären genom att lägga i sin påse vad han eller hon kommit överens om, eller så kan han eller hon hoppa av genom att lämna över en tom påse.

Vän eller fiende?

Vän eller fiende? är ett spelprogram som sändes från 2002 till 2003 på Game Show Network i USA. Det är ett exempel på fångens dilemmaspel som testats på riktiga människor, men i en artificiell miljö. På spelshowen tävlar tre par människor. När ett par elimineras spelar de ett spel som liknar fångens dilemma för att avgöra hur vinsterna delas. Om de båda samarbetar (Friend) delar de på vinsten 50–50. Om den ena samarbetar och den andra misslyckas (Foe), får avhopparen alla vinster, och samarbetspartnern får ingenting. Om båda defekta, lämnar båda med ingenting. Lägg märke till att belöningsmatrisen skiljer sig något från den standard som ges ovan, eftersom belöningarna för fallen "båda defekten" och "samarbeta medan motståndaren misslyckas" är identiska. Detta gör "båda defekten"-fallet till en svag jämvikt, jämfört med att vara en strikt jämvikt i standardfångens dilemma. Om en tävlande vet att deras motståndare kommer att rösta "Foe", så påverkar deras eget val inte deras egna vinster. I en specifik mening Friend or Foe en belöningsmodell mellan fångens dilemma och spelet Chicken .

Belöningsmatrisen är

Par 2 Par 1	"Vän" (samarbeta)	"Foe" (defekt)
"Vän" (samarbeta)	1 1	2 0
"Foe" (defekt)	0 2	0 0

Denna payoff-matris har också använts i de brittiska tv- programmen Trust Me , Shafted , The Bank Job och Golden Balls , och i de amerikanska spelprogrammen Take It All , samt för det vinnande paret i Reality Show-programmen Bachelor Pad och Love Ö . Speldata från Golden Balls -serien har analyserats av ett team av ekonomer, som fann att samarbetet var "överraskande högt" för summor pengar som skulle tyckas vara följdriktiga i den verkliga världen men som var jämförelsevis låga i spelets sammanhang.

Itererad snödriva

Forskare från University of Lausanne och University of Edinburgh har föreslagit att "Iterated Snowdrift Game" kan återspegla verkliga sociala situationer närmare. Även om den här modellen faktiskt är ett kycklingspel , kommer den att beskrivas här. I denna modell är risken att bli utnyttjad genom avhopp lägre och individer vinner alltid på att välja kooperativt. Snödrivespelet föreställer sig två förare som har fastnat på motsatta sidor av en snödriva , som var och en får möjlighet att skotta snö för att rensa en stig eller sitta kvar i sin bil. En spelares högsta vinst kommer från att lämna motståndaren för att rensa all snö själv, men motståndaren belönas fortfarande nominellt för sitt arbete.

Detta kan bättre spegla verkliga scenarier, forskarna ger exemplet med två forskare som samarbetar i en rapport, som båda skulle gynnas om den andra arbetade hårdare. "Men när din samarbetspartner inte gör något arbete, är det förmodligen bättre för dig att göra allt arbete själv. Du kommer fortfarande att sluta med ett avslutat projekt."

Exempel på utbetalningar för snödrivor (A, B) B A Samarbetar Defekter Samarbetar 500, 500 200, 800 Defekter 800, 200 0, 0

Exempel PD-utbetalningar (A, B) B A Samarbetar Defekter Samarbetar 500, 500 −200, 1200 Defekter 1200, -200 0, 0

Koordinationsspel

Huvudartikel: koordinationsspel

I koordinationsspel måste spelarna samordna sina strategier för ett bra resultat. Ett exempel är två bilar som plötsligt möts i en snöstorm; var och en måste välja om de ska svänga åt vänster eller höger. Om båda svänger åt vänster, eller båda åt höger, kolliderar inte bilarna. Den lokala vänster- och högertrafikkonventionen hjälper till att samordna deras agerande.

Symmetriska koordinationsspel inkluderar Stag hunt och Bach eller Stravinsky .

Asymmetriska fångens dilemman

En mer allmän uppsättning spel är asymmetriska. Liksom i fångens dilemma är det bästa resultatet samarbete, och det finns motiv för avhopp. Till skillnad från det symmetriska fångdilemmat har en spelare mer att förlora och/eller mer att vinna än den andra. Vissa sådana spel har beskrivits som ett fångdilemma där en fånge har ett alibi , varifrån termen "alibi-spel".

I experiment kan spelare som får ojämlika utdelningar i upprepade spel försöka maximera vinsten, men endast under förutsättning att båda spelarna får samma utdelning; detta kan leda till en stabil jämviktsstrategi där den missgynnade spelaren defekt varje X-spel, medan den andra alltid samarbetar. Sådant beteende kan bero på experimentets sociala normer kring rättvisa.

Väktarens dilemma

Det är inte bara fångar som står inför dilemman. Vårdnadshavare konfronterar också situationer där det bara finns oattraktiva val att välja mellan. Exempel kan lätt hittas i fall där en agent måste jämna ut spänningar mellan sina egna partners: man kan tänka på två kollegor som jockeyar för karriäravancemang och de problem detta orsakar deras företags verkställande direktör ; två tjänstemän som konkurrerar om befordran och den spänning detta orsakar för chefen för deras byrå ; eller i föräldraskap när två syskon tävlar om uppmärksamhet och den oro detta orsakar deras föräldrar. Om vårdnadshavarens beteende tillfredsställer ena sidan, känner sig den andra sidan utsatt och alienerad.

Ur ett internationella relationsperspektiv introducerar Dr Spyros Katsoulas begreppet väktarens dilemma. Väktarens dilemma definieras som det tillstånd där två stater upprätthåller sin fiendskap mot varandra trots att de delar en starkare gemensam allierad. Som standard är ett dilemma en situation med otillfredsställande val. Väktarens dilemma ligger i att den starkare staten varken kan hålla sig utanför en kris mellan sina allierade eller engagera sig aktivt utan att påverka den bräckliga jämvikten. Om vårdnadshavaren avstår från att rösta kan situationen gå ur kontroll; om väktaren blir inblandad kan varje lutning mot ena sidan ses som en seger eller ett tillfälle för den andra. Utvidgningen av Glenn Snyders koncept om alliansens säkerhetsdilemmat beskrivs resultatet av interaktionen mellan väktaren och de två mindre partnerna som övergiven, instängd och uppmuntrande.

programvara

Flera mjukvarupaket har skapats för att köra prisoner's dilemmasimuleringar och turneringar, av vilka några har tillgänglig källkod.

• Källkoden för den andra turneringen som drivs av Robert Axelrod (skriven av Axelrod och många bidragsgivare i Fortran ) är tillgänglig online
• Prison , ett bibliotek skrivet i Java , senast uppdaterad 1998
• Axelrod-Python , skriven i Python
• Evoplex , ett snabbt agentbaserat modelleringsprogram släppt 2018 av Marcos Cardinot

I fiktion

Hannu Rajaniemi satte inledningsscenen i sin The Quantum Thief -trilogi i ett "dilemmafängelse". Seriens huvudtema har beskrivits som "otillräckligheten i ett binärt universum" och den ultimata antagonisten är en karaktär som kallas All-Defector. Rajaniemi är en Cambridge-utbildad matematiker och har en Ph.D. i matematisk fysik – utbytbarheten av materia och information är ett viktigt inslag i böckerna, som utspelar sig i en "post-singularity" framtid. Den första boken i serien kom ut 2010, med de två uppföljarna, Fraktalprinsen och Orsaksängeln , utgivna 2012 respektive 2014.

Ett spel som är modellerat efter (det upprepade) fångdilemmat är ett centralt fokus i 2012 års videospel Zero Escape: Virtue's Last Reward och en mindre del i dess 2016-uppföljare Zero Escape: Zero Time Dilemma .

I The Mysterious Benedict Society and the Prisoner's Dilemma av Trenton Lee Stewart börjar huvudkaraktärerna med att spela en version av spelet och fly från "fängelset" helt och hållet. Senare blir de verkliga fångar och flyr igen.

I The Adventure Zone : Balance during The Suffering Game subarc presenteras spelarkaraktärerna två gånger med fångens dilemma under sin tid i två liches domän, en gång samarbetande och en gång hoppar av.

I den 8:e romanen från författaren James SA Corey Tiamats vrede . förklarar Winston Duarte fångens dilemma för sin 14-åriga dotter, Teresa, för att träna henne i strategiskt tänkande

En extrem version av fångens dilemma finns med i filmen The Dark Knight från 2008 , där Jokern riggar två färjor, en innehåller fångar och den andra innehåller civila, och beväpnar båda grupperna med medel för att detonera bomben på varandras färjor. I slutändan beslutar de två sidorna att inte agera.

Se även

• Abilene paradox
• Tusenfoting spel
• Jul vapenvila
• Externitet
• Folksats (spelteori)
• Free-rider problem
• Hobbesiansk fälla
• Oskyldiga fångens dilemma
• Liar Game
• Valfritt fångsdilemma
• Fångens dilemma och samarbete
• Allmännyttiga spel
• Present-bytesspel
• Ömsesidig altruism
• Hyressökande
• Sociala preferenser
• Swift trust theory
• De vanligas tragedi
• Samvetslös middagsdilemma
• Resenärens dilemma
• Superrationalitet

Vidare läsning

• Amadae, S. (2016). "Prisoner's Dilemma" , Prisoners of Reason . Cambridge University Press , NY, s. 24–61.
•   Aumann, Robert (1959). "Acceptabla poäng i allmänt kooperativa n -personspel". I Luce, RD; Tucker, AW (red.). Bidrag till Theory 23 of Games IV . Annals of Mathematics Study. Vol. 40. Princeton NJ: Princeton University Press. s. 287–324. MR 0104521 .
•   Axelrod, R. (1984). Samarbetets utveckling . ISBN 0-465-02121-2
• Bicchieri, Cristina (1993). Rationalitet och samordning. Cambridge University Press .
• Chess, David M. (december 1988). "Simulerar beteendets utveckling: problemet med upprepade fångars dilemma" ( PDF) . Komplexa system . 2 (6): 663–70. Arkiverad (PDF) från originalet 2015-05-30.
• Collins, Rory W. (mars 2022). "Fångens dilemmaparadox: rationalitet, moral och ömsesidighet" . Tänk: Filosofi för alla . 21 (61): 45–55. doi : 10.1017/S1477175621000464 .
• Dresher, M. (1961). The Mathematics of Games of Strategy: Theory and Applications Prentice-Hall , Englewood Cliffs, NJ.
• Greif, A. (2006). Institutioner och vägen till den moderna ekonomin: Lärdomar från medeltida handel. Cambridge University Press, Cambridge , Storbritannien.
• Kopelman, Shirli (februari 2020). "Titt för tat och bortom: Anatol Rapoports legendariska verk" . Forskning om förhandling och konflikthantering . 13 (1): 60–84. doi : 10.1111/ncmr.12172 .
•   Poundstone, William (1993). Prisoner's Dilemma (1st Anchor Books ed.). New York: Anchor. ISBN 0-385-41580-X .
• Rapoport, Anatol och Albert M. Chammah (1965). Fångens dilemma . University of Michigan Press .
• Schneider, Mark; Shields, Timothy W. (juni 2022). "Motiv för samarbete i enskottsfångens dilemma" . Journal of Behavioral Finance . 23 (4): 438–456. doi : 10.1080/15427560.2022.2081974 .

externa länkar

• Media relaterade till Prisoner's dilemma på Wikimedia Commons
• Prisoner's Dilemma ( Stanford Encyclopedia of Philosophy )
• The Bowerbird's Dilemma The Prisoner's Dilemma in ornitology – matematisk serie av Larry Gonick.
• The Prisoner's Dilemma The Prisoner's Dilemma med Lego minifigurer.
•    Dixit, Avinash ; Nalebuff, Barry (2008). "Fångens dilemma" . I David R. Henderson (red.). Concise Encyclopedia of Economics (2:a uppl.). Indianapolis: Library of Economics and Liberty . ISBN 978-0865976658 . OCLC 237794267 .
• Game Theory 101: Prisoner's Dilemma
• Dawkins: Nice Guys avslutar först
• Axelrod Iterated Prisoner's Dilemma Python- bibliotek
• Spela Prisoner's Dilemma på oTree (N/A 11-5-17)
• Nicky Case's Evolution of Trust , ett exempel på donationsspelet
• Iterated Prisoner's Dilemma onlinespel av Wayne Davis