Ramsey–Cass–Koopmans modell

Ramsey –Cass–Koopmans-modellen , eller Ramsey-tillväxtmodellen , är en neoklassisk modell för ekonomisk tillväxt baserad i första hand på Frank P. Ramseys arbete, med betydande förlängningar av David Cass och Tjalling Koopmans . Ramsey-Cass-Koopmans-modellen skiljer sig från Solow-Swan-modellen genom att valet av konsumtion är explicit mikrogrundat vid en tidpunkt och på så sätt endogeniserar besparingsgraden . Som ett resultat, till skillnad från i Solow–Swan-modellen, kanske besparingsgraden inte är konstant under övergången till det långsiktiga stabila tillståndet . En annan implikation av modellen är att resultatet är Pareto optimalt eller Pareto effektivt .

Ursprungligen satte Ramsey upp modellen som en socialplanerares problem med att maximera konsumtionsnivåerna över successiva generationer. Först senare antogs en modell av Cass och Koopmans som en beskrivning av en decentraliserad dynamisk ekonomi med en representativ agent . Ramsey-Cass-Koopmans-modellen syftar endast till att förklara långsiktig ekonomisk tillväxt snarare än konjunktursvängningar, och inkluderar inte några källor till störningar som marknadsimperfektioner, heterogenitet bland hushållen eller exogena chocker . Efterföljande forskare utökade därför modellen, vilket möjliggjorde statliga köpchocker, variationer i sysselsättning och andra källor till störningar, vilket är känt som verklig konjunkturcykelteori .

Matematisk beskrivning

Modelluppsättning

I den vanliga inställningen börjar tiden kontinuerligt, för enkelhetens skull, vid $t=0$ och fortsätter för alltid. Enligt antagande är de enda produktiva faktorerna kapital $K$ och arbete $L$ , båda måste vara icke-negativa. Arbetskraften, som utgör hela befolkningen, antas växa i konstant takt $n$ , dvs ${\dot {L}}={\ tfrac {\mathrm {d} L}{\mathrm {d} t}}=nL$ , vilket antyder att $L=L_{0}e^{nt}$ med initial nivå $L_{0}>0$ vid $t=0$ . Låt slutligen $Y$ beteckna aggregerad produktion och $C$ beteckna aggregerad konsumtion.

Variablerna som Ramsey-Cass-Koopmans-modellen i slutändan syftar till att beskriva är ${\displaystyle c={\frac {C}{L}}} ,$ konsumtionen per capita (eller mer exakt, per arbetskraft ), som samt $k={\frac {K}{L}}$ , den så kallade kapitalintensiteten . Det gör det genom att först koppla ihop kapitalackumulering, skrivet ${\dot {K}}={\tfrac {\mathrm {d} K}{\mathrm {d} t}}$ i Newtons notation , med konsumtion $C$ , som beskriver en avvägning mellan konsumtion och investering. Närmare bestämt, eftersom det befintliga kapitalstocken sjunker av avskrivningstakten $\delta$ (antas vara konstant), kräver det investeringar av den aktuella periodens produktion $Y$ . Således,

$${\dot {K}}=Y-\delta K-cL$$

Sambandet mellan de produktiva faktorerna och den aggregerade produktionen beskrivs av den aggregerade produktionsfunktionen , $Y=F(K,L)$ . Ett vanligt val är Cobb–Douglas produktionsfunktion $F(K,L)=AK^{1-\alpha }L^{\alpha }$ , men i allmänhet är alla produktionsfunktioner som uppfyller Inada-villkoren tillåtna. Viktigt är dock att $F$ måste vara homogen med grad 1 , vilket ekonomiskt innebär konstant skala . Med detta antagande kan vi återuttrycka aggregerad produktion i termer per capita

$$F(K,L)=L\cdot F\left({\frac {K}{L}} ,1\right)=L\cdot f(k)$$

Till exempel, om vi använder Cobb–Douglas-produktionsfunktionen med $A=1,\alpha =0,5$ , då $f(k)=k ^{0.5}$ .

För att erhålla den första nyckelekvationen i Ramsey-Cass-Koopmans-modellen måste den dynamiska ekvationen för kapitalstocken uttryckas i termer per capita . Notera kvotregeln för ${\tfrac {\mathrm {d} }{\mathrm {d} t}}\left({\tfrac {K}{L}}\right)$ , vi har

${\dot {k}}=f(k)-(n+\delta )kc$

en icke-linjär differentialekvation som liknar Solow-Svan-modellen .

Maximera välfärden

Om vi ​​bortser från problemet med hur konsumtionen är fördelad, så är nyttograden $U$ en funktion av den aggregerade konsumtionen. Det vill säga $U=U(C,t)$ . För att undvika problemet med oändlighet, diskonterar vi exponentiellt $\rho \in (0,\infty )$ nytta med en diskonteringsränta . Ett högt $\rho$ reflekterar hög otålighet .

Socialplanerarens problem är att maximera den sociala välfärdsfunktionen $-\rho t}U(C,t)\,\mathrm {d} t}$${\displaystyle U_{0}=\int _{0}^{\infty }e^$ { .

Antag att ekonomin är befolkad av identiska odödliga individer med oföränderliga nyttofunktioner $u(c)$ (en representativ agent ), så att den totala nyttan är:

$$U(C,t)=Lu(c)=L_{0}e^{nt}u(c)$$

Verktygsfunktionen antas vara strikt ökande (dvs. det finns ingen salighetspunkt ) och konkav i $c$ , med $\lim _{c\to 0}u_{ c}=\infty$ , där $u_{c}$ är marginell nytta av konsumtion ${\tfrac {\partial u}{\partial c}}$ .

Vi har alltså samhällsplanerarens problem:

$\max _{c}\int _{0}^{\infty }e^{-(\rho -n)t} u(c)\,\mathrm {d} t$

${\text{subject to}}\quad c=f(k) -(n+\delta )k-{\dot {k}}$

där en initial icke-noll kapitalstock $k(0)=k_{0}>0$ ges.

För att säkerställa att integralen är väldefinierad lägger vi på $\rho >n$ .

Lösning

Lösningen, som vanligtvis hittas genom att använda en Hamiltonsk funktion , är en differentialekvation som beskriver den optimala utvecklingen av konsumtion,

${\dot {c}}=\sigma (c)\left[f_{k}(k)-\delta - \rho \right]\cdot c$

Keynes –Ramsey-regeln .

Termen $f_{k}(k)-\delta -\rho$ , där $f_{k}=\partial _{k} f$ är marginalprodukten av kapital , reflekterar marginalavkastningen på nettoinvesteringen , med hänsyn till kapitalavskrivningar och tidsdiskontering.

Här är $\sigma (c)$ elasticiteten för intertemporal substitution , definierad av

$$\sigma (c)=-{\frac {u_ {c}(c)}{c\cdot u_{cc}(c)}}=-{\frac {d\ln c}{d\ln(u'(c))}}$$

Det motsvarar formellt det omvända till relativ riskaversion . Kvantiteten återspeglar krökningen av nyttofunktionen och anger hur mycket den representativa agenten vill jämna ut förbrukningen över tiden. Om agenten har hög relativ riskaversion, har den låg EIS, och skulle därför vara mer villig att jämna ut konsumtionen över tiden.

Man antar ofta att $u$ är strikt monotont ökande och konkav, alltså $\sigma >0$ . I synnerhet, om nyttan är logaritmisk, är den konstant:

$$u(c)=u_{0}\ln c\implies \sigma (c)=1$$

Vi kan skriva om Ramsey-regeln som

$$\underbrace {{\frac {d} {dt}}\ln c} _{\text{förbrukningsfördröjningshastighet}}=\underbrace {\sigma (c)} _{{\text{EIS vid nuvarande förbrukningsnivå}}\quad }\underbrace {[f_{ k}(k)-\delta -\rho ]} _{\text{marginal avkastning på nettoinvestering}}$$

där vi tolkar ${\frac {d}{dt}}\ln c$ som "förbrukningsfördröjningshastigheten", för om den är hög betyder det att agenten förbrukar mycket mindre nu jämfört med senare, vilket i huvudsak är vad fördröjd konsumtion handlar om.

Grafisk analys i fasrum

Fasdiagram av Ramsey-modellen, för fallet $f(k)=k^{0,5}$ och ${ \displaystyle n,\delta ,\rho ,\sigma =1,1,1.1,1}$ .

Fasrymdsdiagram (eller fasdiagram) av Ramsey-modellen. Den blå linjen representerar ekonomins dynamiska justering (eller sadelbana) där alla begränsningar som finns i modellen är uppfyllda. Det är en stabil väg för det dynamiska systemet. De röda linjerna representerar dynamiska banor som utesluts av transversalitetsvillkoret.

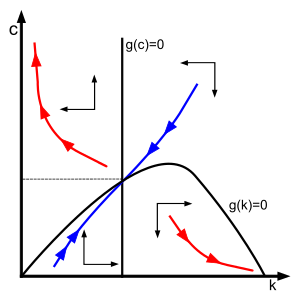
De två kopplade differentialekvationerna för $k$ och $c$ bildar Ramsey-Cass-Koopmans dynamiska system .

${\begin{cases}{\dot { k}}=f(k)-(n+\delta )kc\\{\dot {c}}=\sigma (c)\left[f_{k}(k)-\delta -\rho \right]\ cdot c\end{cases}}$

Ett stabilt tillstånd $(k^{\ast },c^{\ast })$ för systemet hittas genom att ställa in ${\dot {k}}$ och ${\dot {c}}$ lika med noll. Det finns tre lösningar:

$f_{k}\left(k^{\ast }\right)=\delta + \rho \quad {\text{and}}\quad c^{\ast }=f\left(k^{\ast }\right)-(n+\delta )k^{\ast }$

${ \displaystyle (0,0)}$

$f(k^{*})=(n+\delta )k^{* }{\text{ med }}k^{*}>0,c^{*}=0$

Den första är den enda lösningen i det inre av den övre kvadranten. Det är en sadelpunkt (som visas nedan). Den andra är en avvisande punkt. Den tredje är en degenererad stabil jämvikt.

Som standard menas den första lösningen, även om de andra två lösningarna är viktiga att hålla reda på.

Varje optimal bana måste följa det dynamiska systemet. Men eftersom variabeln ${\displaystyle c} är$$displaystyle c (0)}$ kontrollvariabel, vid varje kapitalintensitet ${\displaystyle k},$ för att hitta dess motsvarande optimala bana, måste vi fortfarande hitta dess startkonsumtionshastighet c ( ) . Som det visar sig är den optimala banan den unika som konvergerar till den inre jämviktspunkten. Vilken annan bana som helst konvergerar antingen till allbesparande jämvikt med $k^{*}>0,c^{*}=0$ , eller divergerar till ${\ displaystyle k\to 0,c\to \infty }$ , vilket innebär att ekonomin spenderar allt sitt kapital på ändlig tid. Båda uppnår en lägre total nytta än banan mot den inre jämviktspunkten.

Ett kvalitativt påstående om stabiliteten hos lösningen ${\displaystyle (k^{\ast },c^{\ast })} kräver en linearisering av ett$ Taylorpolynom av första ordningen

${\begin{bmatrix}{\dot {k}}\\{\dot {c}}\end{bmatrix}}\approx \mathbf {J} (k^{\ast },c^{\ast}){\begin{bmatrix}(kk^{\ast })\\(cc ^{\ast })\end{bmatrix}}$

där $\mathbf {J} (k^{\ast },c^{\ast })$ är den jakobianska matrisen utvärderad vid steady state, given av

$\mathbf {J} \left(k^{\ast },c^{\ast }\right)={\begin{bmatrix}\rho -n&-1\\{\frac {1}{\sigma }}f_{kk}(k)\cdot c^{\ast }&0\end{bmatrix }}$

som har determinant $\left|\mathbf {J} \left(k^{\ast },c^{\ast }\right)\right|={\frac {1}{\sigma }}f_{kk}(k)\cdot c^{\ast }<0$ eftersom $c^{*}>0$ , $\sigma$ är positiv genom antagande, och $f_{kk}<0$ eftersom $f$ är konkav (Inada-villkor). Eftersom determinanten är lika med produkten av egenvärdena måste egenvärdena vara reella och motsatta i tecken.

är jämvikten enligt stabila manifoldsatsen en sadelpunkt och det finns en unik stabil arm, eller "sadelbana", som konvergerar mot jämvikten, indikerad av den blå kurvan i fasdiagrammet.

Systemet kallas "sadelbana stabil" eftersom alla instabila banor är uteslutna av villkoret "no Ponzi scheme ":

$\lim _{t\to \infty }k\cdot e^{-\int _{0}^{t }\left(f_{k}-n-\delta \right)\mathrm {d} s}\geq 0$

vilket innebär att nuvärdet av kapitalstocken inte kan vara negativt.

Historia

Spear och Young omprövar historien om optimal tillväxt under 1950- och 1960-talen, och fokuserar delvis på sanningshalten i den påstådda samtidiga och oberoende utvecklingen av Cass "Optimum growth in an aggregative model of capital accumulation" (publicerad 1965 i Review of Economic Studies ), och Tjalling Koopmans "On the concept of optimal economic growth" (publicerad i Study Week on the Econometric Approach to Development Planning, 1965, Rome: Pontifical Academy of Science).

Under sin livstid antydde varken Cass eller Koopmans någonsin att deras resultat som kännetecknar optimal tillväxt i den ensektors, kontinuerliga tillväxtmodellen var något annat än "samtidig och oberoende". Att frågan om prioritet någonsin blev en diskussionspunkt berodde bara på att han i den publicerade versionen av Koopmans arbete citerade kapitlet ur Cass avhandling som senare blev RES- uppsatsen . Koopmans anger i sin uppsats i en fotnot att Cass självständigt erhållit villkor som liknar vad Koopmans finner, och att Cass även överväger det begränsande fallet där diskonteringsräntan går till noll i sin uppsats. Cass noterar för sin del att "efter att den ursprungliga versionen av detta dokument slutförts kom en mycket liknande analys av Koopmans till vår kännedom. Vi utgår från hans resultat när vi diskuterar det begränsande fallet, där den effektiva sociala diskonteringsräntan går till noll." . I intervjun som Cass gav till Macroeconomic Dynamics krediterar han Koopmans för att ha hänvisat honom till Frank Ramseys tidigare arbete, och påstår sig ha skämts över att inte ha känt till det, men säger ingenting för att skingra det grundläggande påståendet att hans arbete och Koopmans var i faktiskt oberoende.

Spear och Young bestrider denna historia, baserat på en tidigare förbisedd version av Koopmans papper, som låg till grund för Koopmans ofta citerade presentation vid en konferens som hölls av Pontifical Academy of Sciences i oktober 1963. I denna Cowles diskussionsuppsats , det finns ett fel. Koopmans hävdar i sitt huvudresultat att Euler-ekvationerna är både nödvändiga och tillräckliga för att karakterisera optimala banor i modellen eftersom alla lösningar på Euler-ekvationerna som inte konvergerar till det optimala stationära tillståndet skulle träffa antingen en nollförbrukning eller noll kapitalgräns i ändlig tid. Detta fel presenterades tydligen vid Vatikankonferensen, även om ingen deltagare kommenterade problemet vid tidpunkten för Koopmans presenterade det. Detta kan man sluta sig till eftersom diskussionen efter varje papperspresentation vid Vatikankonferensen bevaras ordagrant i konferensvolymen.

I Vatikanens volymdiskussion efter presentationen av en artikel av Edmond Malinvaud , uppstår frågan på grund av Malinvauds uttryckliga införande av ett så kallat "transversalitetstillstånd" (som Malinvaud kallar villkor I) i sin tidning. I slutet av presentationen frågar Koopmans Malinvaud om det inte är så att villkor I helt enkelt garanterar att lösningar på Euler-ekvationerna som inte konvergerar till det optimala stationära tillståndet träffar en gräns i ändlig tid. Malinvaud svarar att så inte är fallet, och föreslår att Koopmans tittar på exemplet med loggfunktioner och Cobb-Douglas produktionsfunktioner.

Vid denna tidpunkt inser Koopmans uppenbarligen att han har ett problem, men baserat på en förvirrande bilaga till en senare version av papper som producerades efter Vatikankonferensen, verkar han oförmögen att bestämma sig för hur han ska hantera frågan som tas upp av Malinvauds Condition I.

Från intervjun med Macroeconomic Dynamics med Cass framgår det tydligt att Koopmans träffade Cass avhandlingsrådgivare, Hirofumi Uzawa , vid Econometric Societys vintermöten i januari 1964, där Uzawa meddelade honom att hans student [Cass] redan hade löst detta problem . Uzawa måste då ha försett Koopmans med kopian av Cass' avhandlingskapitel, som han uppenbarligen skickade med i skepnad av IMSSS Technical Report som Koopmans citerade i den publicerade versionen av sin tidning. Ordet "förklädnad" är lämpligt här, eftersom TR-numret som anges i Koopmans citat skulle ha satt utgivningsdatumet för rapporten i början av 1950-talet, vilket det uppenbarligen inte var.

I den publicerade versionen av Koopmans papper, inför han ett nytt villkor Alpha utöver Euler-ekvationerna, och anger att de enda tillåtna banorna bland dem som uppfyller Euler-ekvationerna är den som konvergerar till modellens optimala jämvikt i jämvikt. Detta resultat härleds i Cass' papper genom införandet av ett transversalitetsvillkor som Cass härledde från relevanta delar av en bok av Lev Pontryagin . Spear and Young gissar att Koopmans tog den här vägen eftersom han inte ville se ut att "låna" varken Malinvauds eller Cass transversalitetsteknologi.

Baserat på denna och andra undersökningar av Malinvauds bidrag på 1950-talet – särskilt hans intuition om vikten av transversalitetsvillkoret – föreslår Spear och Young att den neoklassiska tillväxtmodellen bättre kan kallas Ramsey–Malinvaud–Cass-modellen än den etablerade Ramsey– Cass–Koopmans hedersbetygelse.

Vidare läsning

•   Acemoglu, Daron (2009). "Den nyklassiska tillväxtmodellen" . Introduktion till modern ekonomisk tillväxt . Princeton: Princeton University Press. s. 287–326. ISBN 978-0-691-13292-1 .
•   Barro, Robert J. ; Sala-i-Martin, Xavier (2004). "Tillväxtmodeller med konsumentoptimering" . Economic Growth (andra upplagan). New York: McGraw-Hill. s. 85–142. ISBN 978-0-262-02553-9 .
•   Bénassy, ​​Jean-Pascal (2011). "Ramsey-modellen" . Makroekonomisk teori . New York: Oxford University Press. s. 145–160. ISBN 978-0-19-538771-1 .
•   Blanchard, Olivier Jean ; Fischer, Stanley (1989). "Konsumtion och investeringar: Grundläggande modeller för oändlig horisont" . Föreläsningar om makroekonomi . Cambridge: MIT Press. s. 37–89. ISBN 978-0-262-02283-5 .
•   Miao, Jianjun (2014). "Nyklassiska tillväxtmodeller" . Ekonomisk dynamik i diskret tid . Cambridge: MIT Press. s. 353–364. ISBN 978-0-262-02761-8 .
•   Novales, Alfonso; Fernández, Esther; Ruíz, Jesús (2009). "Optimal tillväxt: Kontinuerlig tidsanalys" . Ekonomisk tillväxt: teori och numeriska lösningsmetoder . Berlin: Springer. s. 101–154. ISBN 978-3-540-68665-1 .
•   Romer, David (2011). "Modeller med oändlig horisont och överlappande generationer". Advanced Macroeconomics (fjärde upplagan). New York: McGraw-Hill. s. 49–77. ISBN 978-0-07-351137-5 .

externa länkar

• på YouTube