Sadelpunkt

Den här artikeln handlar om den matematiska egenskapen. För halvön i Antarktis, se Saddle Point . För typen av landform och allmänna användningar av ordet Sadel som används som en teknisk term, se Sadel (landform) .

En sadelpunkt (i rött) på grafen för z = x ² − y ² ( hyperbolisk paraboloid )

Sadelpunkt mellan två kullar (skärningspunkten mellan åtta z- konturen)

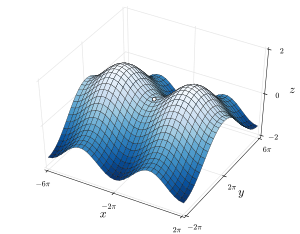
I matematik är en sadelpunkt eller minimaxpunkt en punkt på ytan av grafen för en funktion där lutningarna (derivator) i ortogonala riktningar alla är noll (en kritisk punkt ), men som inte är ett lokalt extremum för funktionen. Ett exempel på en sadelpunkt är när det finns en kritisk punkt med ett relativt minimum längs en axiell riktning (mellan toppar) och vid ett relativt maximum längs korsningsaxeln. En sadelpunkt behöver dock inte vara i denna form. $displaystyle (0,0)}$ exempel har funktionen $f(x,y)=x^{2}+y^{3}$ en kritisk punkt vid ( , ) som är en sadelpunkt eftersom det varken är ett relativt maximum eller relativt minimum, men det har inte ett relativt maximum eller relativt minimum i riktningen y $\displaystyle y} .$

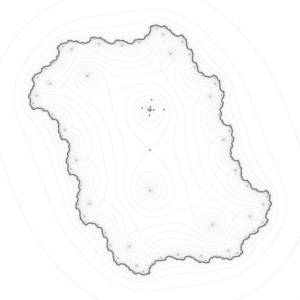
Namnet härrör från det faktum att det prototypiska exemplet i två dimensioner är en yta som kröker sig uppåt i en riktning, och kröker ner i en annan riktning, som liknar en ridsadel eller ett bergspass mellan två toppar som bildar en sadel i landform . När det gäller konturlinjer ger en sadelpunkt i två dimensioner upphov till en konturkarta med ett par linjer som skär varandra i punkten. Sådana korsningar är sällsynta i faktiska ammunitionsundersökningskartor, eftersom höjden på sadelpunkten sannolikt inte kommer att sammanfalla med heltalsmultiplarna som används i sådana kartor. Istället visas sadelpunkten som ett tomt utrymme i mitten av fyra uppsättningar konturlinjer som närmar sig och svänger bort från den. För en grundläggande sadelpunkt förekommer dessa uppsättningar i par, med ett motsatt högt par och ett motsatt lågt par placerade i ortogonala riktningar. De kritiska konturlinjerna behöver i allmänhet inte skära varandra ortogonalt.

Sadelpunkt på konturdiagrammet är punkten där nivåkurvor korsar varandra

Matematisk diskussion

F ( x , y ) med reellt värde för två reella variabler är en sadelpunkt är att beräkna funktionens hessiska matris vid den punkten: om hessian är obestämd , då den punkten är en sadelpunkt. Till exempel, den hessiska matrisen för funktionen $z=x^{2}-y^{2}$ vid den stationära punkten ${ \displaystyle (x,y,z)=(0,0,0)}$ är matrisen

${\begin{bmatrix}2&0\\0&-2\\\end{bmatrix}}$

som är obestämd. Därför är denna punkt en sadelpunkt. Detta kriterium ger endast ett tillräckligt villkor. Till exempel är punkten $(0,0,0)$ en sadelpunkt för funktionen $z=x^{4}-y^{4 },$ men den hessiska matrisen för denna funktion vid ursprunget är nollmatrisen , som inte är obestämd.

I de mest allmänna termerna är en sadelpunkt för en jämn funktion (vars graf är en kurva , yta eller hyperyta ) en stationär punkt så att kurvan/ytan/etc. i närheten av den punkten är inte helt på någon sida av tangentutrymmet vid den punkten.

Plottet för y = x ³ med en sadelpunkt vid 0

I en domän av en dimension är en sadelpunkt en punkt som är både en stationär punkt och en böjningspunkt . Eftersom det är en böjningspunkt är det inte ett lokalt extremum .

Sadelyta

Hyperbolisk paraboloid

En modell av en elliptisk hyperboloid av ett ark

En apsadel

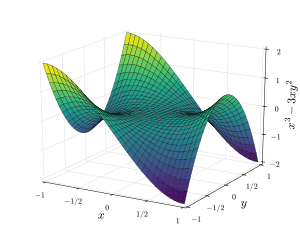
En sadelyta är en slät yta som innehåller en eller flera sadelpunkter.

Klassiska exempel på tvådimensionella sadelytor i det euklidiska rummet är andra ordningens ytor, den hyperboliska paraboloiden ${\displaystyle z=x^{2}-y^{2}} ($ som ofta refereras till som " sadelytan " eller "standardsadelytan") och hyperboloiden för ett ark . Pringles potatischips eller crisp är ett vardagligt exempel på en hyperbolisk paraboloid form .

Sadelytor har negativ Gaussisk krökning som skiljer dem från konvexa/elliptiska ytor som har positiv Gaussisk krökning. En klassisk tredje ordningens sadelyta är apsadeln .

Exempel

nollsummespel för två spelare definierat på ett kontinuerligt utrymme är jämviktspunkten en sadelpunkt.

För ett andra ordningens linjärt autonomt system är en kritisk punkt en sadelpunkt om den karakteristiska ekvationen har ett positivt och ett negativt reellt egenvärde.

Vid optimering under förutsättning av jämlikhetsbegränsningar beskriver första ordningens villkor en sadelpunkt hos Lagrangian .

Andra användningsområden

I dynamiska system , om dynamiken ges av en differentierbar karta f så är en punkt hyperbolisk om och endast om differentialen för ƒ ⁿ (där n är punktens period) inte har något egenvärde på den (komplexa) enhetscirkeln när den beräknas vid punkten. Då är en sadelpunkt en hyperbolisk periodisk punkt vars stabila och instabila grenrör har en dimension som inte är noll.

En sadelpunkt i en matris är ett element som är både det största elementet i sin kolumn och det minsta elementet i sin rad.

Se även

• Sadelpunktsmetoden är en förlängning av Laplaces metod för att approximera integraler
• Extremum
• Derivattest
• Hyperbolisk jämviktspunkt
• Hyperboliskt plan
• Minimaxsats
• Max–min ojämlikhet
• Apsadel
• Bergspasssats

Källor

•   Gray, Lawrence F.; Flanigan, Francis J.; Kazdan, Jerry L.; Frank, David H.; Fristedt, Bert (1990), Kalkyl två: linjära och icke-linjära funktioner , Berlin: Springer-Verlag, sid. 375 , ISBN 0-387-97388-5
•   Hilbert, David ; Cohn-Vossen, Stephan (1952), Geometry and the Imagination (2nd ed.), New York, NY: Chelsea , ISBN 978-0-8284-1087-8
• von Petersdorff, Tobias (2006), "Critical Points of Autonomous Systems", differentialekvationer för forskare och ingenjörer (Math 246 föreläsningsanteckningar)
•   Widder, DV (1989), Advanced calculus , New York, NY: Dover Publications, sid. 128, ISBN 0-486-66103-2
• Agarwal, A., Study on the Nash Equilibrium (föreläsningsanteckningar)

Vidare läsning

•   Hilbert, David ; Cohn-Vossen, Stephan (1952). Geometry and the Imagination (2:a uppl.). Chelsea. ISBN 0-8284-1087-9 .

externa länkar

• Media relaterade till Saddle Point på Wikimedia Commons