Tetraedriskt förminskad dodekaeder

|
|

|
|
| Dorman Luke självdubbel form | |
|---|---|
| Tetraedriskt stjärnbildad ikosaeder | |
| Tetraedriskt förminskad dodekaeder | |

|
|
| Conway polyeder notation | pT |
| Ansikten | 16: 4 {3} + 12 fyrhörningar |
| Kanter | 30 |
| Vertices | 16 |
| Vertex-konfiguration |
3.4.4.4 4.4.4 |
| Symmetrigrupp | T , [3,3] + , (332), ordning 12 |
| Dubbel polyeder | Självdubbel |
| Egenskaper | konvex |
   Nät |
|
Inom geometri är en tetraedriskt förminskad dodekaeder (också tetraedriskt stellerad icosahedron eller propellotetraeder ) en topologiskt självdubbel polyeder gjord av 16 hörn, 30 kanter och 16 sidor (4 liksidiga trianglar och 12 identiska fyrsidiga ).
mittsfärens radie är 1. Drakarna förblir likbenta.
Den har kiral tetraedrisk symmetri , och så kan dess geometri konstrueras från pyritoedrisk symmetri av pseudoicosahedron med 4 ansikten stellated , eller från pyritohedron , med 4 hörn förminskade . Inom sin tetraedriska symmetri har den geometriskt varierande proportioner. Av Dorman Luke dubbelkonstruktion kan en unik geometrisk proportion definieras. Drakens ytor har kanter med längdförhållande ~ 1:0,633.
Topologiskt är trianglarna alltid liksidiga, medan fyrhörningarna är oregelbundna, även om de två intilliggande kanterna som möts vid hörn av en tetraeder är lika.
Som en självdubbel hexadekaeder är den en av 302404 former, 1476 med minst ordning 2 symmetri, och den enda med tetraedrisk symmetri.
Som en förminskad regelbunden dodekaeder , med 4 hörn borttagna, är fyrsidiga ytor trapetser .
Som en stellation av den vanliga ikosaedern är den en av 32 stellationer definierade med tetraedrisk symmetri. Den har drakeansikten.
I Conway polyhedron notation kan det representeras som pT , applicera George W. Harts propelleroperatör på en vanlig tetraeder .
Besläktade polytoper och bikakor
Denna polyeder representerar vertexfiguren av en hyperbolisk likformig bikakekaka , den delvis förminskade icosahedriska bikakeformen , pd{3,5,3}, med 12 femkantiga antiprismor och 4 dodekaederceller som möts vid varje vertex.
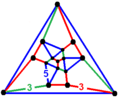
- Vertexfigur projicerad som Schlegel-diagram
Anteckningar
externa länkar
- tetraedriskt stympad dodekaeder och stjärnbildad ikosaeder
- Generering av en ikosaeder genom skärningspunkten mellan fem tetraedrar: geometriska och kristallografiska egenskaper hos de mellanliggande polyedrarna
- [1] VRML -modell som trunkerad vanlig dodekaeder
- [2] VRML-modell som tetraedriskt stjärnbildad ikosaeder
