Lista över enhetliga polyedrar efter vertexfigur

Polyeder
Klass	Antal och egenskaper
Platonska fasta ämnen	( 5 , konvex, vanlig)
Arkimedeiska fasta ämnen	( 13 , konvex, uniform)
Kepler–Poinsot polyedrar	( 4 , regelbunden, icke-konvex)
Uniforma polyedrar	( 75 , uniform)
Prismatoid : prismor , antiprismor etc.	( 4 oändliga uniformsklasser)
Polyedra kakel	( 11 vanliga , i planet)
Kvasi-regelbundna polyedrar	( 8 )
Johnson fasta ämnen	( 92 , konvex, olikformig)
Pyramider och bipyramider	( oändlig )
Stellationer	Stellationer
Polyedriska föreningar	( 5 vanliga )
Deltahedra	( Deltaedrar , liksidiga triangelytor)
Snub polyedra	( 12 uniformer , inte spegelvänd)
Zonohedron	( Zonohedra , ansikten har 180° symmetri)
Dubbel polyeder
Självdubbel polyeder	( oändlig )
Katalansk solid	( 13 , arkimedeisk dual)

Det finns många relationer mellan de enhetliga polyedrarna . Vissa erhålls genom att trunkera hörnen på den regelbundna eller kvasi-regelbundna polyedern. Andra delar samma hörn och kanter som andra polyeder. Grupperingen nedan visar några av dessa relationer.

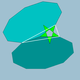
Topfiguren av en polyeder

Relationerna kan göras uppenbara genom att undersöka vertexfigurerna som erhålls genom att lista ytorna intill varje vertex (kom ihåg att för enhetliga polyedrar är alla hörn desamma, det vill säga vertextransitiva ). Till exempel har kuben vertexfigur 4.4.4, vilket vill säga tre intilliggande kvadratiska ytor. De möjliga ansiktena är

• 3 - liksidig triangel
• 4 - kvadrat
• 5 - vanlig femhörning
• 6 - vanlig hexagon
• 8 - vanlig oktagon
• 10 - vanlig dekagon
• 5/2 - pentagram
• 8/3 - oktagram
• 10/3 - dekagram

Vissa ansikten kommer att visas med omvänd orientering som skrivs här som

• -3 - en triangel med omvänd orientering (skrivs ofta som 3/2)

Andra passerar genom ursprunget som vi skriver som

• 6* - hexagon som passerar genom origo

Wythoff -symbolen relaterar polyedern till sfäriska trianglar . Wythoff-symboler skrivs p|qr, pq|r, pqr| där den sfäriska triangeln har vinklarna π/p,π/q,π/r, anger stapeln läget för topparna i förhållande till triangeln.

Exempel vertex figurer

Johnson (2000) klassificerade enhetliga polyedrar enligt följande:

1. Reguljära (regelbundna polygonala vertexfigurer): p ^q , Wythoff-symbol q|p 2
2. Kvasireguljära (rektangulära eller ditrigonala vertexfigurer): pqpq 2|pq, eller pqpqpq, Wythoff-symbol 3|pq
3. Versi-regular (ortodiagonala vertexfigurer), pq*.-pq*, Wythoff-symbol qq|p
4. Trunkerad regelbunden (likbenta triangulära vertexfigurer): ppq, Wythoff-symbol q 2|p
5. Versi-quasi-regular (dipteroidala vertexfigurer), pqpr Wythoff symbol qr|p
6. Kvasi-kvasireguljära (trapesformade vertexfigurer): p*.qp*.-r qr|p eller pq*.-pq* pqr|
7. Trunkerad kvasi-regelbunden (skalen triangulära vertexfigurer), pqr Wythoff symbol pqr|
8. Snub kvasi-reguljära (femkantiga, sexkantiga eller åttkantiga vertexfigurer), Wythoff-symbol pqr|
9. Prismor (stympad hosohedra),
10. Antiprismor och korsade antiprismor (snub dihedra)

Formatet för varje figur följer samma grundmönster

1. bild av polyeder
2. namn på polyeder
3. alternativa namn (inom parentes)
4. Wythoff symbol
5. Numreringssystem: W - nummer som används av Wenninger i polyedermodeller , U - enhetlig indexering, K - Kaleido indexering, C - numrering som används i Coxeter et al. 'Uniform Polyhedra'.
6. Antal hörn V, kanter E, Ytor F och antal ytor efter typ.
7. Eulerkarakteristik χ = V - E + F

Hönsfigurerna är till vänster, följt av punktgrupperna i tre dimensioner#De sju återstående punktgrupperna , antingen tetraedrisk T _d , oktaedrisk O _h eller icosahedral I _h .

Trunkerade former

Regelbundna polyedrar och deras trunkerade former

Kolumn A listar alla vanliga polyedrar, kolumn B listar deras trunkerade former. Reguljära polyedrar har alla vertexfigurer p ^r : ppp etc. och Wythoff-symbol p|q r. De trunkerade formerna har vertexfigur qqr (där q=2p och r) och Wythoff pq|r.

vertex figur	grupp	A: vanlig: ppp	B: trunkerad regelbunden: ppr
3.3.3 3.6.6	T d	Tetrahedron 3|2 3 W1, U01, K06, C15 V 4,E 6,F 4=4{3} χ =2	Trunkerad tetraeder 2 3|3 W6, U02, K07, C16 V 12,E 18,F 8=4{3}+4{6} χ =2
3.3.3.3 4.6.6	O h	Octahedron 4|2 3, 3 4 W2, U05, K10, C17 V 6,E 12,F 8=8{3} χ =2	Trunkerad oktaeder 2 4|3 W7, U08, K13, C20 V 24,E 36,F 14=6{4}+8{6} χ =2
4.4.4 3.8.8	O h	Hexaeder (kub) 3|2 4 W3, U06, K11, C18 V 8,E 12,F 6=6{4} χ =2	Trunkerad hexaeder 2 3|4 W8, U09, K14, C21 V 24,E 36,F 14=8{3}+6{8} χ =2
3.3.3.3.3 5.6.6	jag h	Icosahedron 5|2 3 W4, U22, K27, C25 V 12,E 30,F 20=20{3} χ =2	Trunkerad icosahedron 2 5|3 W9, U25, K30, C27 E 60,V 90,F 32=12{5}+20{6} χ =2
5.5.5 3.10.10	jag h	Dodekaeder 3|2 5 W5, U23, K28, C26 V 20,E 30,F 12=12{5} χ =2	Trunkerad dodekaeder 2 3|5 W10, U26, K31, C29 V 60,E 90,F 32=20{3}+12{10} χ =2
5.5.5.5.5 5/2.10.10	jag h	Stor dodekaeder 5 / 2 |2 5 W21, U35, K40, C44 V 12,E 30,F 12=12{5} χ =-6	Trunkerad stor dodekaeder 2 5/2 |5 W75, U37, K42 , C47 V 60,E 90 , F 24=12{ 5/2 } +12{10} χ = -6
3.3.3.3.3 5/2.6.6.	jag h	Great icosahedron (16:e stellationen av icosahedron) 5 / 2 |2 3 W41, U53, K58, C69 V 12,E 30,F 20=20{3} χ =2	stympad icosahedron 2 5/2 | 3 W95, U55, K60, C71 V 60,E 90 , F 32=12{ 5/2 }+20{6} χ =2
5/2,5/2,5/2,5/2,5/2	jag h	Liten stellerad dodekaeder 5|2 5 / 2 W20, U34, K39, C43 V 12,E 30,F 12=12{ 5 / 2 } χ =-6
5/2,5/2,5/2	jag h	stjärnformad dodekaeder 3|2 5/2 W22 , U52, K57, C68 V 20 ,E 30,F 12=12{ 5/2 } χ =2

Dessutom finns det tre kvasi-trunkerade former. Dessa klassas också som trunkerade-regelbundna polyedrar.

vertex figurer	Grupp O h	Grupp I h	Grupp I h
3,8/3,8/3 5,10/3,10/3 3,10/3,10/3	Stellat trunkerad hexaeder (Quasitruncated hexahedron) (stellatruncated cube) 2 3| 4/3 W92, U19, K24, C66 V 24 , E 36,F 14=8{3}+6{ 8/3 } χ = 2	Liten stjärnformad stympad dodekaeder (Quasitruncated small stellated dodecahedron) (Liten stellatruncated dodecahedron) 2 5| 5/3 W97, U58 , K63 V 60,E 90,F 24=12{5} +12 { 10/3 } χ = -6	Stor stjärnformad stympad dodekaeder (Quasitruncated great stellated dodecahedron) (Great stellatruncated dodecahedron) 2 3| 5/3 W104 , U66, K71, C83 V 60,E 90,F 32=20{3}+12 { 10/3 } χ = 2

Trunkerade former av kvasi-regelbundna polyedrar

Kolumn A listar några kvasi-regelbundna polyedrar, kolumn B visar normala trunkerade former, kolumn C visar kvasi-trunkerade former, kolumn D visar en annan trunkeringsmetod. Dessa trunkerade former har alla en vertexfigur pqr och en Wythoff-symbol pqr|.

vertex figur	grupp	A: quasi-regular: pqpq	B: trunkerad kvasi-regelbunden: pqr	C: trunkerad kvasi-regelbunden: pqr	D: trunkerad kvasi-regelbunden: pqr
3.4.3.4 4.6.8 4.6.8/3 8.6.8/3	O h	Cuboctahedron 2|3 4 W11, U07, K12, C19 V 12,E 24,F 14=8{3}+6{4} χ =2	Stympad kuboktaeder (Stora rhombicuboctahedron) 2 3 4| W15, U11, K16, C23 V 48,E 72,F 26=12{4}+8{6}+6{8} χ =2	Stor stympad cuboctahedron (Quasitruncated cuboctahedron) 2 3 4 / 3 | W93, U20, K25, C67 V 48,E 72,F 26=12{4}+8{6}+6 { 8/3 } χ = 2	Cubitruncated cuboctahedron (Cuboctatruncated cuboctahedron) 3 4 4 / 3 | W79, U16, K21, C52 V 48,E 72 , F 20=8{6}+6{8}+6{ 8/3 } χ = -4
3.5.3.5 4.6.10 4.6.10/3 10.6.10/3	jag h	Icosidodecahedron 2|3 5 W12, U24, K29, C28 V 30,E 60,F 32=20{3}+12{5} χ =2	Trunkerad icosidodecahedron (Great rhombicosidodecahedron) 2 3 5| W16, U28, K33, C31 V 120,E 180,F 62=30{4}+20{6}+12{10} χ =2	Stor stympad icosidodecahedron (Great quasitruncated icosidodecahedron) 2 3 5 / 3 | W108, U68, K73, C87 V 120,E 180,F 62=30{4}+20{6}+12{ 10/3 } χ = 2	Icositruncated dodecadodecahedron (Icosidodecatruncated icosidodecahedron) 3 5 5 / 3 | W84, U45, K50, C57 V 120,E 180,F 44=20{6}+12{10}+12 { 10/3 } χ = -16
5/2.5.5/2.5 4.10.10/3	jag h	Dodecadodecahedron 2 5| 5/2 W73, U36, K41, C45 V 30 ,E 60, F 24=12{5}+12 { 5/2 } χ = -6		Trunkerad dodekaeder (Quasitruncated dodecahedron) 2 5 5 / 3 | W98, U59, K64, C75 V 120,E 180,F 54=30{4}+12{10}+12 { 10/3 } χ = -6
3,5/2,3,5/2	jag h	Great icosidodecahedron 2 3| 5/2 W94 , U54, K59, C70 V 30,E 60, F 32=20{3}+12 { 5/2 } χ = 2

Polyedrar som delar kanter och hörn

Regelbunden

Dessa nämns alla på annat håll, men denna tabell visar några samband. De är alla regelbundna förutom tetrahemihexaedern som är versi-regelbunden.

vertex figur	V	E	grupp	regelbunden	regelbunden/versi-regelbunden
3.3.3.3 3,4*.-3,4*	6	12	O h	Octahedron 4|2 3 W2, U05, K10, C17 F 8=8{3} χ =2	Tetrahemihexahedron 3/2 3 |2 W67, U04, K09, C36 F 7=4{3}+3{4} χ =1
3.3.3.3.3 5.5.5.5.5	12	30	jag h	Icosahedron 5|2 3 W4, U22, K27 F 20=20{3} χ =2	Stor dodekaeder 5 / 2 |2 5 W21, U35, K40, C44 F 12=12{5} χ =-6
5/2.5/2.5/2.5/2.5/2 3.3.3.3.3	12	30	jag h	Liten stellerad dodekaeder 5|2 5 / 2 W20, U34, K39, C43 F 12=12{ 5 / 2 } χ =-6	Great icosahedron (16:e stellationen av icosahedron) 5 / 2 |2 3 W41, U53, K58, C69 F 20=20{3} χ =2

Kvasiregelbundet och versiregelbundet

Rektangulära vertexfigurer eller korsade rektanglar första kolumnen är kvasi-regelbundna andra och tredje kolumner är hemiedrar med ansikten som passerar genom ursprunget, kallade versi-regular av vissa författare.

vertex figur	V	E	grupp	kvasi-regelbunden: pqpq	versi-regular: ps*.-ps*	versi-regular: qs*.-qs*
3.4.3.4 3.6*.-3.6* 4.6*.-4.6*	12	24	O h	Cuboctahedron 2|3 4 W11, U07, K12, C19 F 14=8{3}+6{4} χ =2	Octahemioctahedron 3 / 2 3|3 W68, U03, K08, C37 F 12=8{3}+4{6} χ =0	Cubohemioctahedron 4 / 3 4|3 W78, U15, K20, C51 F 10=6{4}+4{6} χ =-2
3.5.3.5 3.10*.-3.10* 5.10*.-5.10*	30	60	jag h	Icosidodecahedron 2|3 5 W12, U24, K29, C28 F 32=20{3}+12{5} χ =2	Liten icosihemidodecahedron 3 / 2 3|5 W89, U49, K54, C63 F 26=20{3}+6{10} χ =-4	Liten dodekahemidodekaeder 5 / 4 5|5 W91, U51, K56, 65 F 18=12{5}+6{10} χ =-12
3,5/2,3,5/2 3,10*.-3,10* 5/2,10*.-5/2,10*	30	60	Ih	Great icosidodecahedron 2| 5/2 3 W94 , U54, K59, C70 F 32=20{3} +12 { 5/2 } χ = 2	Stor icosihemidodecahedron 3 3| 5/3 W106 , U71 , K76, C85 F 26=20{3}+6 { 10/3 } χ = -4	Stor dodecahemidodecahedron 5 / 3 5 / 2 | 5/3 W107 , U70 , K75 , C86 F 18=12{ 5/2 } +6{ 10/3 } χ = -12
5,5/2,5,5/2 5,6*.-5,6* 5/2,6*.-5/2,6*	30	60	Ih	Dodecadodecahedron 2| 5/2 5 W73, U36 , K41 , C45 F 24=12{5}+12{ 5/2 } χ = -6	Great dodecahemicosahedron 5 / 4 5|3 W102, U65, K70, C81 F 22=12{5}+10{6} χ =-8	Liten dodecahemicosahedron 5/3 5/2 | 3 W100, U62, K67, C78 F 22 =12{ 5/2 } +10 {6} χ = -8

Ditrigonal regelbunden och versi-regelbunden

Ditrigonala (det vill säga di(2) -tri(3)-ogonala) vertexfigurer är den trefaldiga analogen av en rektangel. Dessa är alla kvasi-regelbundna eftersom alla kanter är isomorfa. Sammansättningen av 5-kuber delar samma uppsättning kanter och hörn. Korsformerna har en icke- orienterbar vertexfigur så "-"-notationen har inte använts och "*"-ytorna passerar nära snarare än genom origo.

vertex figur	V	E	grupp	dirigonal	korsad-dirigonal	korsad-dirigonal
5/2.3.5/2.3.5/2.3 5/2.5*.5/2.5*.5/2.5* 3.5*.3.5*.3.5*	20	60	Ih	Liten ditrigonal icosidodecahedron 3| 5/2 3 W70, U30 , K35, C39 F 32=20{3}+12 { 5/2 } χ = -8	Ditrigonal dodecadodecahedron 3| 5/3 5 W80, U41 , K46, C53 F 24=12{5}+12 { 5/2 } χ = -16	Stor ditrigonal icosidodecahedron 3/2 |3 5 W87, U47, K52, C61 F 32 =20{3}+12{5} χ =-8

versi-quasi-regular och quasi-quasi-regular

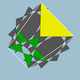
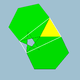
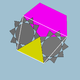
Grupp III: trapetsformade eller korsade trapetsformade vertexfigurer. Den första kolumnen inkluderar de konvexa rombiska polyedrarna, skapade genom att infoga två rutor i spetsfigurerna i Cuboctahedron och Icosidodecahedron.

vertex figur	V	E	grupp	trapetsform: pqrq	korsad trapets: ps*.-rs*	korsad trapets: qs*.-qs*
3.4.4.4 3.8*.-4.8* 4.8*.-4.8*	24	48	O h	Liten rhombicuboctahedron (rhombicuboctahedron) 3 4|2 W13, U10, K15, C22 F 26=8{3}+(6+12){4} χ =2	Liten cubicuboctahedron 3/2 4 |4 W69, U13, K18, C38 F 20=8{3}+6{4}+6{8} χ =-4	Liten rhombihexahedron 2 3 / 2 4| W86, U18, K23, C60 F 18=12{4}+6{8} χ =-6
3,8/3,4,8/3 3,4*.-4,4* 8/3,4*.-8/3,4*	24	48	Åh	Stor cubicuboctahedron 3 4| 4/3 W77, U14, K19 , C50 F 20=8{3}+6{4}+6{ 8/3 } χ = -4	Ickekonvex stor rombikuboktaeder (Quasirhombicuboctahedron) 3 / 2 4|2 W85, U17, K22, C59 F 26=8{3}+(6+12){4} χ =2	Stor rhombihexahedron 2 4 / 3 3 / 2 | W103 , U21, K26 , C82 F 18=12{4}+6{ 8/3 } χ =-6
3.4.5.4 3.10*.-5.10* 4.10*.-4.10*	60	120	jag h	Liten rhombicosidodecahedron (rhombicosidodecahedron) 3 5|2 W14, U27, K32, C30 F 62=20{3}+30{4}+12{5} χ =2	Liten dodecicosidodecahedron 3 / 2 5|5 W72, U33, K38, C42 F 44=20{3}+12{5}+12{10} χ =-16	Liten rhombidodecahedron 2 5 / 2 5| W74, U39, K44, C46 F 42=30{4}+12{10} χ =-18
5/2.4.5.4 5/2.6*.-5.6* 4.6*.-4.6*	60	120	Ih	Rhombidodecadodecahedron 5/2 5 | 2 W76, U38, K43, C48 F 54=30{4}+12{5}+12{ 5/2 } χ = -6	Icosidodecadodecahedron 5/3 5 |3 W83, U44 , K49, C56 F 44=12{5}+12{ 5/2 }+20 {6} χ = -16	Rhombicosahedron 2 3 5 / 2 | W96, U56, K61, C72 F 50=30{4}+20{6} χ =-10
3.10/3.5/2.10/3 3.4*.-5/2.4* 10/3.4*.-10/3.4*	60	120	Ih	Stor dodecicosidodecahedron 5 / 2 3| 5/3 W99 , U61 , K66 , C77 F 44=20{3}+12{ 5/2 }+12{ 10/3 } χ = -16	Ickekonvex stor rhombicosidodecahedron (Quasirhombicosidodecahedron) 5/3 3 | 2 W105, U67, K72, C84 F 62=20{3}+30{4}+12{ 5/2 } χ = 2	Stora rhombidodecahedron 2 3 / 2 5 / 3 | W109, U73 , K78, C89 F 42=30{4}+12{ 10/3 } χ = -18
3.6.5/2.6 3.10*.-5/2.10* 6.10*.-6.10*	60	120	Ih	Liten icosicosidodecahedron 5/2 3 |3 W71, U31, K36, C40 F 52=20{3}+12{ 5/2 }+20 {6} χ = -8	Liten ditrigonal dodecicosidodecahedron 5/3 3 | 5 W82, U43, K48, C55 F 44=20{3}+12{ 5/2 }+12{10} χ = -16	Liten dodecikosaeder 3 3 / 2 5| W90, U50, K55, C64 F 32=20{6}+12{10} χ =-28
3.10/3.5.10/3 3.6*.-5.6* 10/3.6*.-10/3.6*	60	120	Ih	Stor ditrigonal dodecicosidodecahedron 3 5| 5/3 W81, U42 , K47, C54 F 44 =20{3}+12{5}+12{ 10/3 } χ = -16	Great icosicosidodecahedron 3/2 5|3 W88, U48, K53, C62 F 52 =20{3}+12{5}+20{6} χ =-8	Stor dodecikosahedron 3 5 / 3 5 / 2 | W101, U63 , K68, C79 F 32=20{6}+12{ 10/3 } χ =-28