Arean av en cirkel

I geometri är området som omges av en cirkel med radien r π r ² . Här representerar den grekiska bokstaven π det konstanta förhållandet mellan varje cirkels omkrets och dess diameter , ungefär lika med 3,14159.

En metod för att härleda denna formel, som har sitt ursprung med Arkimedes , innebär att se cirkeln som gränsen för en sekvens av regelbundna polygoner med ett ökande antal sidor. Arean av en vanlig polygon är halva dess omkrets multiplicerat med avståndet från dess centrum till dess sidor, och eftersom sekvensen tenderar till en cirkel, motsvarar motsvarande formel – att arean är halva omkretsen gånger radien – nämligen A = 1 / 2 × 2π r × r , håller för en cirkel.

Även om det ofta hänvisas till som arean av en cirkel i informella sammanhang, hänvisar termen disk i strängt taget till den inre delen av cirkeln, medan cirkeln endast är reserverad för gränsen, som är en kurva och inte täcker något område i sig. Därför arean av en skiva den mer exakta frasen för området som omges av en cirkel.

Historia

Modern matematik kan erhålla området med hjälp av metoderna för integralräkning eller dess mer sofistikerade avkomma, verklig analys . Emellertid studerades området för en skiva av de gamla grekerna . Eudoxus av Cnidus på femte århundradet f.Kr. hade funnit att en skivas area är proportionell mot dess radie i kvadrat. Arkimedes använde den euklidiska geometrins verktyg för att visa att arean inuti en cirkel är lika med en rätvinklig triangel   vars bas har längden på cirkelns omkrets och vars höjd är lika med cirkelns radie i hans bok Measurement of a Circle . Omkretsen är 2 π r , och arean av en triangel är hälften av basen gånger höjden, vilket ger arean π r ² för skivan. Före Archimedes Hippokrates från Chios den första som visade att en skivas yta är proportionell mot kvadraten på dess diameter, som en del av hans kvadratur av Hippokrates lune , men identifierade inte proportionalitetskonstanten .

Historiska argument

En mängd olika argument har framförts historiskt för att fastställa ekvationen $A=\pi r^{2}$ till olika grader av matematisk rigor. Den mest kända av dessa är Arkimedes utmattningsmetod , en av de tidigaste användningarna av det matematiska begreppet en gräns , såväl som ursprunget till Arkimedes axiom som förblir en del av den standardmässiga analytiska behandlingen av det reella talsystemet . Det ursprungliga beviset för Arkimedes är inte rigoröst enligt moderna standarder, eftersom det antar att vi kan jämföra längden på en cirkelbåge med längden på en sekant och en tangentlinje, och liknande uttalanden om området, vilket är geometriskt uppenbart.

Använda polygoner

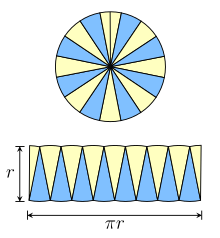
Arean av en vanlig polygon är halva dess omkrets gånger apotem . När antalet sidor av den reguljära polygonen ökar, tenderar polygonen till en cirkel, och apotemet tenderar mot radien. Detta tyder på att arean på en skiva är halva omkretsen av dess gränsande cirkel gånger radien.

Arkimedes bevis

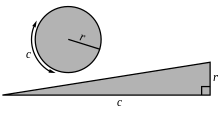
Efter Arkimedes argument i The Measurement of a Circle (ca 260 f.Kr.), jämför området som omges av en cirkel med en rätvinklig triangel vars bas har längden på cirkelns omkrets och vars höjd är lika med cirkelns radie. Om arean av cirkeln inte är lika med triangeln, måste den vara antingen större eller mindre. Vi eliminerar var och en av dessa genom motsägelse, och lämnar jämlikhet som den enda möjligheten. Vi använder vanliga polygoner på samma sätt.

Inte större

Cirkel med kvadrat och oktagon inskrivna, som visar areagap

Antag att arean C som omges av cirkeln är större än arean T = ¹ ⁄ ₂ cr av triangeln. Låt E beteckna överskottsbeloppet. Skriv in en kvadrat i cirkeln, så att dess fyra hörn ligger på cirkeln. Mellan kvadraten och cirkeln finns fyra segment. Om den totala arean av dessa mellanrum, G4 _, är större än E , dela varje båge på mitten. Detta gör den inskrivna kvadraten till en inskriven oktagon och producerar åtta segment med ett mindre totalt gap, G ₈ . Fortsätt dela tills den totala gaparean, G _n , är mindre än E . Nu måste arean för den inskrivna polygonen, P _n = C − G _n , vara större än triangelns.

${\begin{aligned}E&{}=CT\\&{}>G_{n}\\P_ {n}&{}=C-G_{n}\\&{}>CE\\P_{n}&{}>T\end{aligned}}$

Men detta tvingar fram en motsägelse, enligt följande. Rita en vinkelrät från mitten till mitten av en sida av polygonen; dess längd, h , är mindre än cirkelradien. Låt också varje sida av polygonen ha längden s ; då är summan av sidorna, ns , mindre än cirkelns omkrets. Polygonarean består av n lika stora trianglar med höjden h och basen _s , alltså lika med ^1⁄2 nhs . Men eftersom h < r och ns < c , polygonarean måste vara mindre än triangelarean, ¹ ⁄ ₂ cr , en motsägelse. Därför måste vårt antagande att C kan vara större än T vara fel.

Inte mindre

Cirkel med fyrkant och oktagon omskrivna, visar areagap

Antag att arean som omges av cirkeln är mindre än arean T av triangeln. Låt D beteckna underskottsbeloppet. Omskriv en kvadrat, så att mittpunkten av varje kant ligger på cirkeln. Om det totala areagapet mellan kvadraten och cirkeln, G ₄ , är större än D , skär av hörnen med cirkeltangenter för att göra en omskriven oktagon och fortsätt att skära tills gaparean är mindre än D . Polygonens area, P _n , måste vara mindre än T .

${\begin{aligned}D&{}=TC\\&{}>G_{n}\\P_ {n}&{}=C+G_{n}\\&{}<C+D\\P_{n}&{}<T\end{aligned}}$

Även detta tvingar fram en motsägelse. Ty en vinkelrät mot mittpunkten av varje polygonsida är en radie med längden r . Och eftersom den totala sidolängden är större än omkretsen, består polygonen av n identiska trianglar med total area större än T . Återigen har vi en motsägelse, så vårt antagande att C kan vara mindre än T måste också vara fel.

Därför måste det vara så att arean som omges av cirkeln är exakt densamma som arean av triangeln. Detta avslutar beviset.

Omarrangemang bevis

Cirkla området genom omarrangering

Grafer över sidan , s ; apotem , en ; och area , A av regelbundna polygoner av n sidor och circumradius 1, med basen , b av en rektangel med samma area . Den gröna linjen visar fallet n = 6 .

Efter Satō Moshun ( Smith & Mikami 1914 , s. 130–132), Nicholas of Cusa och Leonardo da Vinci ( Beckmann 1976 , s. 19), kan vi använda inskrivna regelbundna polygoner på ett annat sätt. Anta att vi skriver in en hexagon . Skär hexagonen i sex trianglar genom att dela den från mitten. Två motsatta trianglar berör båda två gemensamma diametrar; skjut dem längs en så att de radiella kanterna är intill varandra. De bildar nu ett parallellogram , med hexagonsidorna som gör två motsatta kanter, varav en är basen, s . Två radiella kanter bildar lutande sidor, och höjden h är lika med dess apotem (som i Arkimedes-beviset). Faktum är att vi också kan sätta ihop alla trianglar till ett stort parallellogram genom att sätta på varandra följande par bredvid varandra. Detsamma gäller om vi ökar den till åtta sidor och så vidare. För en polygon med 2 n sidor kommer parallellogrammet att ha en bas med längden ns och en höjd h . När antalet sidor ökar närmar sig parallellogrambasens längd halva cirkelns omkrets och dess höjd närmar sig cirkelradien. I gränsen blir parallellogrammet en rektangel med bredd π r och höjd r .

Enhet skivarea genom att arrangera om n polygoner.

polygon			parallellogram
n	sida		bas	höjd	område
4	1,4142136		2,8284271	0,7071068	2,0000000
6	1,0000000		3,0000000	0,8660254	2,5980762
8	0,7653669		3,0614675	0,9238795	2,8284271
10	0,6180340		3,0901699	0,9510565	2,9389263
12	0,5176381		3,1058285	0,9659258	3,0000000
14	0,4450419		3,1152931	0,9749279	3,0371862
16	0,3901806		3,1214452	0,9807853	3,0614675
96	0,0654382		3,1410320	0,9994646	3,1393502
∞	1/∞		π	1	π

Moderna bevis

Det finns olika ekvivalenta definitioner av konstanten π. Den konventionella definitionen i pre-calculus geometri är förhållandet mellan en cirkels omkrets och dess diameter:

$\pi ={\frac {C}{D}}.$

Men eftersom omkretsen av en cirkel inte är ett primitivt analytiskt begrepp, är denna definition inte lämplig i moderna rigorösa behandlingar. En modern standarddefinition är att π är lika med två gånger den minst positiva roten av cosinusfunktionen eller, ekvivalent, halvperioden för sinusfunktionen ( eller cosinusfunktionen). Cosinusfunktionen kan definieras antingen som en potensserie eller som lösningen av en viss differentialekvation . Detta undviker alla hänvisningar till cirklar i definitionen av π , så att påståenden om förhållandet mellan π till cirklarnas omkrets och area är faktiskt teorem, snarare än definitioner, som följer av de analytiska definitionerna av begrepp som "area" och "omkrets".

De analytiska definitionerna ses som likvärdiga, om det är överenskommet att cirkelns omkrets mäts som en likriktbar kurva med hjälp av integralen

$C=2\int _{-R}^{R}{\frac {R\,dx}{\sqrt {R^{2}-x^{2}}}}=2R\int _{ -1}^{1}{\frac {dx}{\sqrt {1-x^{2}}}}.$

Integralen som visas till höger är en abelsk integral vars värde är en halvperiod av sinusfunktionen, lika med π . Således ses ${\displaystyle C=2\pi R=\pi D} vara sann som ett sats.$

Flera av argumenten som följer använder endast begrepp från elementär kalkyl för att reproducera formeln ${\displaystyle A=\pi r^{2}} ,$ men i många fall för att betrakta dessa som faktiska bevis förlitar de sig implicit på det faktum att man kan utveckla trigonometriska funktioner och grundkonstanten π på ett sätt som är helt oberoende av deras relation till geometrin. Vi har angett där det är lämpligt hur vart och ett av dessa bevis kan göras helt oberoende av all trigonometri, men i vissa fall kräver det mer sofistikerade matematiska idéer än de som erbjuds av elementär kalkyl.

Löksäker

Skivans område via ringintegration

Med hjälp av kalkyl kan vi summera arean stegvis och dela upp skivan i tunna koncentriska ringar som lager av en lök . Detta är metoden för skalintegration i två dimensioner. För en oändligt tunn ring av "löken" med radien t är den ackumulerade arean 2 π t dt , ringens omkretslängd gånger dess oändliga bredd (man kan approximera denna ring med en rektangel med bredd=2 π t och höjd = dt ). Detta ger en elementär integral för en skiva med radien r .

${\begin{aligned}\mathrm {Area} (r)&{}=\int _{0}^{r}2\pi t\,dt\\&{}=2\pi \left[ {\frac {t^{2}}{2}}\right]_{0}^{r}\\&{}=\pi r^{2}.\end{aligned}}$

Det är rigoröst motiverat av den multivariata substitutionsregeln i polära koordinater. Arean ges nämligen av en dubbelintegral av konstantfunktionen 1 över själva skivan. Om D betecknar skivan, kan dubbelintegralen beräknas i polära koordinater enligt följande:

${\begin{aligned}\mathrm {Area} (r)&{}=\iint _{D}1\ d(x,y)\\&{}=\iint _{D}t \ dt\ d\theta \\&{}=\int _{0}^{r}\int _{0}^{2\pi }t\ d\theta \ dt\\&{}=\int _ {0}^{r}\left[t\theta \right]_{0}^{2\pi }dt\\&{}=\int _{0}^{r}2\pi t\,dt \\\end{aligned}}$

vilket är samma resultat som ovan.

En likvärdig rigorös motivering, utan att förlita sig på de speciella koordinaterna för trigonometri, använder koareaformeln . Definiera en funktion $\rho :\mathbb {R} ^{2}\to \mathbb {R}$ med ${\textstyle \rho (x,y)={\sqrt {x^{2}+y^{2}}}}$ . Notera ρ är en Lipschitz-funktion vars gradient är en enhetsvektor $|\nabla \rho |=1$ ( nästan överallt ). Låt D vara skivan $\rho <1$ i $\mathbb {R} ^{2}$ . Vi kommer att visa att ${\mathcal {L}}^{2}(D)=\pi$ , där ${\mathcal {L}}^{2}$ är det tvådimensionella Lebesguemåttet i $\mathbb {R} ^{2}$ . Vi ska anta att det endimensionella Hausdorff-måttet för cirkeln $\rho =r$ är $2\pi r$ , cirkelns omkrets med radien r . (Detta kan tas som definitionen av omkrets.) Sedan, med koareaformeln,

${\begin{aligned}{\mathcal {L}}^{2}(D)&=\iint _{D}|\nabla \rho |\,d{\mathcal {L}}^{2 }\\&=\int _{\mathbb {R} }{\mathcal {H}}^{1}(\rho ^{-1}(r)\cap D)\,dr\\&=\int _{0}^{1}{\mathcal {H}}^{1}(\rho ^{-1}(r))\,dr\\&=\int _{0}^{1}2\ pi r\,dr=\pi .\end{aligned}}$

Triangelsäker

Cirkel olindad för att bilda en triangel

Cirkeln och triangeln är lika i area.

I likhet med lökbeviset som beskrivs ovan skulle vi kunna utnyttja kalkyl på ett annat sätt för att komma fram till formeln för arean av en skiva. Överväg att packa upp de koncentriska cirklarna till raka remsor. Detta kommer att bilda en rätvinklig triangel med r som höjd och 2 π r (som är den yttre skivan av lök) som bas.

Att hitta arean för denna triangel kommer att ge skivans area

${\begin{aligned}{\text{Area}}&{}={\frac {1}{2} }\cdot {\text{bas}}\cdot {\text{höjd}}\\&{}={\frac {1}{2}}\cdot 2\pi r\cdot r\\&{}= \pi r^{2}\end{aligned}}$

De motsatta och intilliggande vinklarna för denna triangel är respektive i grader 9,0430611..., 80,956939... och i radianer 0,1578311... OEIS : A233527 , 1,4129651... OEIS : A233528 .

Explicit föreställer vi oss att dela upp en cirkel i trianglar, var och en med en höjd lika med cirkelns radie och en bas som är oändligt liten. Arean för var och en av dessa trianglar är lika med $cdot du}$ \ displaystyle 1/2\cdot r Genom att summera (integrera) alla områden i dessa trianglar kommer vi fram till formeln för cirkelns area:

${\begin{aligned}\mathrm {Area} (r)&{}=\int _{0}^{2\pi r}{\frac {1}{2}}r\,du\\ &{}=\left[{\frac {1}{2}}ru\right]_{0}^{2\pi r}\\&{}=\pi r^{2}.\end{aligned }}$

Det kan också motiveras med en dubbelintegral av konstantfunktionen 1 över disken genom att vända integrationsordningen och använda en förändring av variabler i den ovan itererade integralen:

${\begin{aligned}\mathrm {Area} (r)&{}=\iint _{D}1\ d(x,y)\\&{}=\iint _{D}t\ dt \ d\theta \\&{}=\int _{0}^{2\pi }\int _{0}^{r}t\ dt\ d\theta \\&{}=\int _{0 }^{2\pi }{\frac {1}{2}}r^{2}\ d\theta \\\end{aligned}}$

Genom att göra substitutionen $u=r\theta ,\ du=r\ d\theta$ omvandlas integralen till

$\int _{0}^{2\pi r}{\frac {1}{2}}{\frac {r^{2}}{r}}du=\int _{0}^{2\pi r}{\frac {1}{2}}r\ du$

vilket är detsamma som ovanstående resultat.

Triangelbeviset kan omformuleras som en tillämpning av Greens sats i flödesdivergensform (dvs en tvådimensionell version av divergenssatsen ), på ett sätt som undviker allt omnämnande av trigonometri och konstanten π . Betrakta vektorfältet ${\displaystyle \mathbf {r} =x\mathbf {i} +y\mathbf {j} } i$ planet. Så divergensen för r är lika med två, och därför är arean av en skiva D lika med

$A={\frac {1}{2}}\iint _{D}\operatörsnamn {div} \mathbf {r} \,dA.$

Enligt Greens teorem är detta detsamma som det utåtriktade flödet av r över cirkeln som avgränsar D :

$A={\frac {1}{2}}\oint _{\partial D}\mathbf {r} \cdot \mathbf {n} \,ds$

där n är enhetens normala och ds är båglängdsmåttet. För en cirkel med radien R centrerad vid origo har vi $|\mathbf {r} |=R$ och ${\displaystyle \mathbf {n} =\mathbf {r} /R} ,$ så ovanstående likhet är

$A={\frac {1}{2}}\oint _{\partial D}\mathbf {r} \cdot {\frac {\mathbf {r} }{R}}\,ds={\ frac {R}{2}}\oint _{\partial D}\,ds.$

Integralen av ds över hela cirkeln $\partial D$ är bara båglängden, som är dess omkrets, så detta visar att arean A som omges av cirkeln är lika med $R/ 2$ gånger cirkelns omkrets.

1/2 annat d𝜃 · r ² · d𝜃 bevis som använder trianglar anser att arean som omges av en cirkel utgörs av ett oändligt antal trianglar (dvs trianglarna har var och en vinkel på i mitten av cirkeln), var och en med arean (härlett från uttrycket för arean av en triangel: 1 / 2 · a · b · sin 𝜃 = 1 / 2 · r · r · sin( d𝜃 = 1/2 ) . · r ² · d𝜃 ) Observera att sin( d𝜃 ) ≈ d𝜃 på grund av liten vinkelapproximation . Genom att summera trianglarnas area kan uttrycket för cirkelns area därför hittas:

$${\begin{aligned}\mathrm {Area} &{}=\int _{0}^{2\pi }{\frac {1}{2}}r^{2}\,d\theta \\&{}=\left[{\frac {1}{2}}r^{2}\theta \right]_{0}^{2\pi }\\&{}=\pi r^{ 2}.\end{aligned}}$$

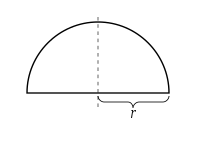
Halvcirkelbevis

Observera att arean av en halvcirkel med radien r kan beräknas av integralen ${\textstyle \int _{-r}^{r}{\sqrt {r^{2} -x^{2}}}\,dx}$ .

En halvcirkel med radien r

Med trigonometrisk substitution ersätter vi $x=r\sin \theta$ , därav $dx=r\cos \theta \,d\theta .$

$${\begin{aligned}\int _{-r}^{r}{\sqrt {r^{2}-x^{2}}}\,dx&=\int _{-{\frac { \pi }{2}}}^{\frac {\pi }{2}}{\sqrt {r^{2}\left(1-\sin ^{2}\theta \right)}}\cdot r \cos \theta \,d\theta \\&=2r^{2}\int _{0}^{\frac {\pi }{2}}\cos ^{2}\theta \,d\theta \ \&={\frac {\pi r^{2}}{2}}.\end{aligned}}$$

Det sista steget följer eftersom den trigonometriska identiteten $\cos(\theta )=\sin(\pi /2-\theta )$ antyder att $\cos ^{2}\theta$ och $\sin ^{2}\theta$ har lika stora integraler över intervallet $[0,\pi /2]$ , med integrering genom substitution . Men å andra sidan, eftersom ${\displaystyle \cos ^{2}\theta +\sin ^{2}\theta =1} ,$ är summan av de två integralerna längden på det intervallet, vilket är $\pi /2$ . Följaktligen är integralen av $\cos ^{2}\theta$ är lika med halva längden av det intervallet, vilket är $\pi /4$ .

Därför är arean av en cirkel med radien r , som är två gånger arean av halvcirkeln, lika med $2\cdot {\frac {\pi r^{ 2}}{2}}=\pi r^{2}$ .

Detta specifika bevis kan tyckas ställa frågan, om sinus- och cosinusfunktionerna som är involverade i den trigonometriska substitutionen anses vara definierade i relation till cirklar. Men, som nämnts tidigare, är det möjligt att definiera sinus, cosinus och π på ett sätt som är helt oberoende av trigonometri, i vilket fall beviset är giltigt genom förändringen av variablers formel och Fubinis sats , under antagande av de grundläggande egenskaperna hos sinus och cosinus (vilket också kan bevisas utan att anta något om deras relation till cirklar).

Isoperimetrisk ojämlikhet

Cirkeln är den slutna kurvan med minsta omkrets som omsluter den maximala ytan. Detta är känt som den isoperimetriska ojämlikheten , som säger att om en likriktbar Jordan-kurva i det euklidiska planet har omkrets C och omsluter ett område A (av Jordan-kurvans sats )

$4\pi A\leq C^{2}.$

Dessutom gäller likhet i denna olikhet om och endast om kurvan är en cirkel, i vilket fall $A=\pi r^{2}$ och $C=2 \pi r$ .

Snabb uppskattning

Beräkningarna som Arkimedes använde för att uppskatta området numeriskt var mödosamma, och han slutade med en polygon på 96 sidor. En snabbare metod använder idéer av Willebrord Snell ( Cyclometricus , 1621), vidareutvecklad av Christiaan Huygens ( De Circuli Magnitudine Inventa , 1654), beskrivna i Gerretsen & Verdenduin (1983 , s. 243–250).

Arkimedes fördubblingsmetod

Givet en cirkel, låt u _n vara omkretsen av en inskriven regelbunden n- gon och låt U _n vara omkretsen av en omskriven regelbunden n- gon. Då u _n och U _n nedre och övre gränser för cirkelns omkrets som blir skarpare och skarpare när n ökar, och deras medelvärde ( u _n + U _n )/2 är en särskilt bra approximation till omkretsen. För att beräkna u _n och U _n för stort n , härledde Arkimedes följande dubbleringsformler:

$u_{2n}={\sqrt {U_{2n}u_{n}}}$ ( geometriskt medelvärde ), och

${\displaystyle U_{2n}={\frac {2U_{n}u_{n}}{U_{n}+u_{n}}}} ($ harmoniskt medelvärde ).

Med utgångspunkt från en hexagon, dubblade Archimedes n fyra gånger för att få en 96-gon, vilket gav honom en bra approximation till cirkelns omkrets.

I modern notation kan vi reproducera hans beräkning (och gå vidare) enligt följande. För en enhetscirkel har en inskriven hexagon u ₆ = 6 och en omskriven hexagon har U ₆ = 4 √ 3 . Fördubbling sju gånger ger

Arkimedes fördubblade sju gånger; n = 6×2 ^k .

k	n	u n	U n	u n + U n / 4
0	6	6,0000000	6,9282032	3,2320508
1	12	6,2116571	6,4307806	3,1606094
2	24	6,2652572	6,3193199	3,1461443
3	48	6,2787004	6,2921724	3,1427182
4	96	6,2820639	6,2854292	3,1418733
5	192	6,2829049	6,2837461	3,1416628
6	384	6,2831152	6,2833255	3,1416102
7	768	6,2831678	6,2832204	3,1415970

(Här approximerar u _n + U _n / 2 omkretsen av enhetscirkeln, vilket är 2 π , så u _n + U _n / 4 approximerar π .)

Den sista posten i tabellen har ³⁵⁵ ⁄ ₁₁₃ som en av sina bästa rationella approximationer ; dvs det finns ingen bättre approximation bland rationella tal med nämnare upp till 113. Talet ³⁵⁵ ⁄ ₁₁₃ är också en utmärkt approximation till π , tillskriven den kinesiske matematikern Zu Chongzhi , som döpte den till Milü . Denna approximation är bättre än något annat rationellt tal med nämnaren mindre än 16 604.

Snell–Huygens förfining

Snell föreslog (och Huygens bevisade) en snävare gräns än Arkimedes:

$n{\frac {3\sin {\frac {\pi }{n}}}{2+\cos {\frac {\pi }{n}}}}<\pi <n\left(2) \sin {\frac {\pi }{3n}}+\tan {\frac {\pi }{3n}}\right).$

Detta för n = 48 ger en bättre approximation (ca 3,14159292) än Arkimedes metod för n = 768.

Härledning av Arkimedes dubbleringsformler

Cirkel med liknande trianglar: omskriven sida, inskriven sida och komplement, inskriven delad sida och komplement

Låt en sida av en inskriven regelbunden n- gon ha längden s _n och rör vid cirkeln vid punkterna A och B. Låt A′ vara punkten mittemot A på cirkeln, så att A′A är en diameter och A′AB är en inskriven triangel på en diameter. Enligt Thales sats är detta en rätvinklig triangel med rät vinkel vid B. Låt längden av A′B vara c _n , som vi kallar komplementet till s _n ; alltså c _n ² + s _n ² = (2 r ) ² . Låt C halvera bågen från A till B och låt C′ vara punkten mittemot C på cirkeln. Sålunda är längden av CA s _{2 n} , längden av C'A är c _{​​2 n} , och C'CA är i sig en rätvinklig triangel på diametern C'C. Eftersom C halverar bågen från A till B, halverar C′C ackordet vinkelrätt från A till B, säg vid P. Triangeln C′AP är alltså en rätvinklig triangel och är liknande till C′CA eftersom de delar vinkeln vid C′. Således är alla tre motsvarande sidor i samma proportion; i synnerhet har vi C′A : C′C = C′P : C′A och AP : C′A = CA : C′C. Cirkelns centrum, O, delar A′A, så vi har också triangel OAP som liknar A′AB, med OP halva längden av A′B. När det gäller sidlängder ger detta oss

${\begin{aligned}c_{2n}^{2}&{}=\left(r+{\frac {1}{2}}c_{n}\right)2r\\c_{2n}& {}={\frac {s_{n}}{s_{2n}}}.\end{aligned}}$

I den första ekvationen är C′P C′O+OP, längden r + ¹ ⁄ ₂ c _n och C′C är diametern, 2 r . För en enhetscirkel har vi den berömda dubbleringsekvationen av Ludolph van Ceulen ,

$c_{2n}={\sqrt {2+c_{n}}}.$

Om vi ​​nu omger en regelbunden n- gon, med sidan A″B″ parallell med AB, så är OAB och OA″B″ liknande trianglar, med A″B″ : AB = OC : OP. Kalla den omskrivna sidan S _n ; då är detta S _n : s _n = 1 : ¹ ⁄ ₂ c _n . (Vi har återigen använt att OP är halva längden av A′B.) Så får vi

$c_{n}=2{\frac {s_{n}}{S_{n}}}.$

Kalla den inskrivna omkretsen u _n = ns _n , och den omskrivna omkretsen U _n = nS _n . Sedan kombinera ekvationer, vi har

$c_{2n}={\frac {s_{n}}{s_{2n}}}=2{\frac {s_{ 2n}}{S_{2n}}},$

så att

$u_{2n}^{2}=u_{n}U_{2n}.$

Detta ger en geometrisk medelekvation .

Vi kan också dra slutsatser

$2{\frac {s_{2n}}{S_{2n}}}{\frac {s_{n}} {s_{2n}}}=2+2{\frac {s_{n}}{S_{n}}},$

eller

${\frac {2}{U_{2n}}}={\frac {1}{u_{n}}}+{\frac {1}{U_{n}}}.$

Detta ger en harmonisk medelekvation.

Dartuppskattning

Enhet cirkel area Monte Carlo integration. Uppskattningen av dessa 900 prover är 4× 709 / 900 = 3,15111...

När effektivare metoder för att hitta områden inte är tillgängliga kan vi ta till att "kasta pilar". Denna Monte Carlo-metod använder det faktum att om slumpmässiga prover tas jämnt utspridda över ytan av en kvadrat där en skiva finns, så approximerar andelen prover som träffar skivan förhållandet mellan skivans yta och kvadratens yta. . Detta bör betraktas som en sista utvägsmetod för att beräkna arean på en skiva (eller vilken form som helst), eftersom det kräver ett enormt antal sampel för att få användbar noggrannhet; en uppskattning bra till 10 ^{− n} kräver cirka 100 ⁿ slumpmässiga urval ( Thijssen 2006 , sid. 273).

Finit omarrangemang

Vi har sett att genom att partitionera skivan i ett oändligt antal bitar kan vi återsätta bitarna till en rektangel. Ett anmärkningsvärt faktum som upptäcktes relativt nyligen ( Laczkovich 1990 ) är att vi kan dissekera skivan till ett stort men ändligt antal bitar och sedan sätta ihop bitarna igen till en kvadrat med lika stor yta. Detta kallas Tarskis cirkelkvadrerande problem . Naturen hos Laczkovichs bevis är sådan att det bevisar existensen av en sådan partition (i själva verket av många sådana partitioner) men inte uppvisar någon speciell partition.

Icke-euklidiska kretsar

Cirklar kan definieras i icke-euklidisk geometri , och i synnerhet i de hyperboliska och elliptiska planen.

Till exempel är enhetssfären $S^{2}(1)$ en modell för det tvådimensionella elliptiska planet. Den har en inneboende metrik som uppstår genom att mäta geodetisk längd. De geodetiska cirklarna är parallellerna i ett geodetiskt koordinatsystem .

Mer exakt, fixera en punkt $\mathbf {z} \in S^{2}(1)$ som vi placerar i zenit. Associerat till den zenit är ett geodesiskt polärt koordinatsystem $(\phi ,\theta )$ , $0\leq \phi \leq \pi$ , $0\leq \theta <2\pi$ , där z är punkten $\phi =0$ . I dessa koordinater, det geodetiska avståndet från z till någon annan punkt $\mathbf {x} \in S^{2}(1)$ som har koordinater $( \phi ,\theta )$ är värdet på $\phi$ vid x . En sfärisk cirkel är uppsättningen punkter ett geodetiskt avstånd R från zenitpunkten z . På motsvarande sätt, med en fast inbäddning i ${\displaystyle \mathbb {R} ^{3}} , är$ den sfäriska cirkeln med radien $R\leq \pi$ centrerad vid z mängden x i $S^{2}(1)$ så att $\mathbf {x} \cdot \mathbf {z} =\cos R$ .

Vi kan också mäta arean på den sfäriska skivan som är innesluten i en sfärisk cirkel, med hjälp av det inneboende ytareamåttet på sfären. Skivans area med radie R ges då av

$A=\int _{0}^{2\pi}\int _{0}^{R}\sin(\phi )d\phi \,d\theta =2\pi (1-\cos R).$

Mer allmänt, om en sfär $S^{2}(\rho )$ har en krökningsradie $\rho$ , så ges arean av skivan med radien R av

$A=2\pi \rho ^{2}(1-\cos(R/\rho )).$

Observera att, som en tillämpning av L'Hôpitals regel , tenderar detta till det euklidiska området $\pi R^{2}$ i den platta gränsen $\rho \to \infty$ .

Det hyperboliska fallet är liknande, med arean av en skiva med inre radie R i hyperbolplanet (konstant krökning ${\displaystyle -1} )$

$A=2\pi (1-\cosh R)$

där cosh är hyperbolisk cosinus . Mer generellt, för den konstanta krökningen $-k$ hyperboliska planet, är svaret

$A=2\pi k^{-2}(1-\cosh(kR)).$

Dessa identiteter är viktiga för att jämföra ojämlikheter i geometri. Till exempel är arean som omges av en cirkel med radien R i ett platt utrymme alltid större än arean av en sfärisk cirkel och mindre än en hyperbolisk cirkel, förutsatt att alla tre cirklarna har samma (inneboende) radie. Det är,

$2\pi (1-\cos R)<\pi R^{2}<2\pi (1 -\cosh R)$

för alla $R>0$ . Intuitivt beror detta på att sfären tenderar att kröka tillbaka på sig själv, vilket ger cirklar med mindre yta än de i planet, medan det hyperboliska planet, när det är nedsänkt i rymden, utvecklar fransar som producerar ytterligare yta. Det är mer allmänt sant att arean av cirkeln med en fast radie R är en strikt minskande funktion av krökningen.

I alla fall, om $k$ är krökningen (konstant, positiv eller negativ), så är den isoperimetriska olikheten för en domän med area A och omkrets L

$L^{2}\geq 4\pi A-kA^{2}$

där jämlikhet uppnås just för cirkeln.

Generaliseringar

Vi kan sträcka en skiva för att bilda en ellips . Eftersom denna sträcka är en linjär transformation av planet, har den en distorsionsfaktor som kommer att förändra arean men bevara förhållandena mellan områden. Denna observation kan användas för att beräkna arean av en godtycklig ellips från arean av en enhetscirkel.

Betrakta enhetscirkeln omgiven av en kvadrat med sidolängden 2. Transformationen skickar cirkeln till en ellips genom att sträcka eller krympa de horisontella och vertikala diametrarna till ellipsens stora och mindre axlar. Fyrkanten skickas till en rektangel som omger ellipsen. Förhållandet mellan cirkelns area och kvadraten är π /4, vilket betyder att förhållandet mellan ellipsen och rektangeln också är π /4. Antag att a och b är längden på ellipsens stora och små axlar. Eftersom arean av rektangeln är ab , är arean av ellipsen π ab /4.

Vi kan också överväga analoga mått i högre dimensioner. Till exempel kan vi vilja hitta volymen inuti en sfär. När vi har en formel för ytarean kan vi använda samma typ av "lök"-metod som vi använde för skivan.

Bibliografi

• 
  Archimedes (1897), "Measurement of a circle" , i Heath, TL (red.), The Works of Archimedes , Cambridge University Press (ursprungligen publicerad av Cambridge University Press , 1897, baserat på JL Heibergs grekiska version.)
•   Beckmann, Petr (1976), A History of Pi , St. Martin's Griffin , ISBN 978-0-312-38185-1
• 
    Gerretsen, J.; Verdenduin, P. (1983), "Kapitel 8: Polygoner och polyedrar", i H. Behnke; F. Bachmann; K. Fladt; H. Kunle (red.), Fundamentals of Mathematics, Volym II: Geometry , översatt av SH Gould, MIT Press , s. 243–250, ISBN 978-0-262-52094-2 (Ursprungligen Grundzüge der Mathematik , Vandenhoeck & Ruprecht , Göttingen, 1971.)
•    Laczkovich, Miklós (1990), "Equidecomposability and discrepans : A solution to Tarski's circle squaring problem" , Journal für die reine und angewandte Mathematik , 1990 ( 404): 77–117, doi : 10.1515/crll.401.71 .401.71 .401 .71.71 .401 .71 . , S2CID 117762563
•   Lang, Serge (1985), "Cirkelns längd", Math! : Encounters with High School Students , Springer-Verlag , ISBN 978-0-387-96129-3
•   Smith, David Eugene ; Mikami, Yoshio (1914), A history of Japanese mathematics , Chicago: Open Court Publishing , s. 130–132, ISBN 978-0-87548-170-8
•   Thijssen, JM (2006), Computational Physics , Cambridge University Press, sid. 273, ISBN 978-0-521-57588-1

externa länkar

• Vetenskapsnyheter om Tarski-problem Arkiverad 2008-04-13 på Wayback Machine