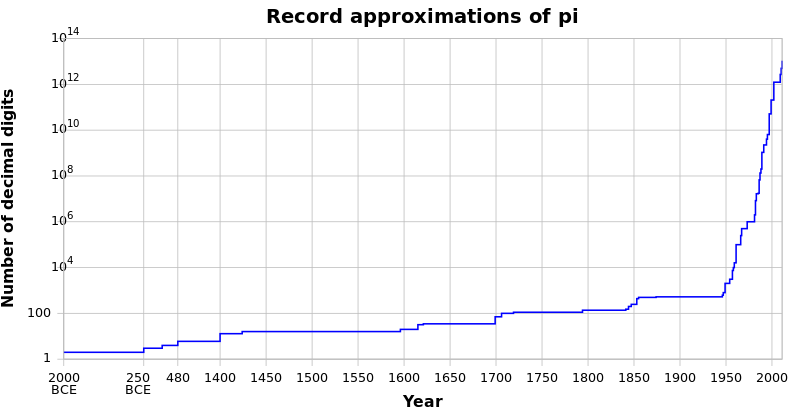
Kronologi för beräkning av π

Tabellen nedan är en kort kronologi över beräknade numeriska värden för, eller gränser för, den matematiska konstanten pi ( π ). För mer detaljerade förklaringar till några av dessa beräkningar, se Approximationer av π .

De sista 100 decimalsiffrorna i den senaste beräkningen av världsrekordet 2022 är:

4658718895 1242883556 4671544483 9873493812 1206904813 2656719174 5255431487 2142102057 729 550645

Graf som visar hur rekordprecisionen för numeriska approximationer till pi mätt i decimaler (avbildad på en logaritmisk skala), utvecklades i mänsklighetens historia. Tiden före 1400 är komprimerad.

Före 1400

Datum	WHO	Beskrivning/Beräkningsmetod som används	Värde	Decimaler ( världsrekord i fetstil )
2000? BCЕ	Forntida egyptier	4 × ( 8 ⁄ 9 ) 2	3,1605...	1
2000? BCЕ	Forntida babylonier	3 + 1 ⁄ 8	3,125	1
2000? BCЕ	Forntida sumerer	3 + 23/216	3,1065	1
1200? BCЕ	Forntida kinesiska	3	3	0
800–600 f.Kr	Shatapatha Brahmana – 7.1.1.18	Instruktioner om hur man bygger ett cirkulärt altare av avlånga tegelstenar: "Han sätter på (den cirkulära platsen) fyra (tegelstenar) som löper österut 1; två bakom som löper tvärs (från söder till norr), och två (sådana) framför. Nu är de fyra som han sätter på som löper österut kroppen; och När det gäller att det finns fyra av dessa, beror det på att denna kropp (vår) består av fyra delar 2. De två baktill är låren, och de två framför armarna, och var kroppen är det (inkluderar ) huvudet."	25 ⁄ 8 = 3,125	1
800? BCЕ	Shulba Sutras	( 6 ⁄ (2 + √ 2 ) ) 2	3,088311 ...	0
550? BCЕ	Bibeln (1 Kungaboken 7:23)	"...ett smält hav, tio alnar från det ena brättet till det andra: det var runt omkring,... en linje på trettio alnar gick runt det"	3	0
434 fvt	Anaxagoras försökte kvadratiska cirkeln	kompass och rakled	Anaxagoras erbjöd ingen lösning	0
400 f.Kr. till 400 f.Kr	Vyasa	verser: 6.12.40-45 i Bhishma Parva från Mahabharata - erbjudandet: " ... Månen har överlämnats av minne till elva tusen yojanas i diameter. Dess perifera cirkel råkar vara trettiotre tusen yojanas när den beräknas ... . Solen är åtta tusen yojanas och ytterligare två tusen yojanas i diameter. Därav kommer dess perifera cirkel att vara lika med trettio tusen yojanas. ... "	3	0
c. 250 f.Kr	Arkimedes	223 ⁄ 71 < π < 22 ⁄ 7	3,140845... < π < 3,142857...	2
15 fvt	Vitruvius	25⁄8 _ _	3,125	1
mellan 1 och 5	Liu Xin	Okänd metod som ger en siffra för en jialiang som innebär ett värde för π π ≈ 162 ⁄ ( √ 50 +0,095) 2 .	3,1547...	1
130	Zhang Heng ( Boken om den senare Han )	√ 10 = 3,162277... 736 ⁄ 232	3,1622...	1
150	Ptolemaios	377 ⁄ 120	3,141666...	3
250	Wang fan	142 ⁄ 45	3,155555...	1
263	Liu Hui	3,141024 < π < 3,142074 3927 ⁄ 1250	3,1416	3
400	Han Chengtian	111035 ⁄ 35329	3,142885...	2
480	Zu Chongzhi	3,1415926 < π < 3,1415927 355 ⁄ 113	3,1415926	7
499	Aryabhata	62832 ⁄ 20000	3,1416	3
640	Brahmagupta	√ 10	3,162277...	1
800	Al Khwarizmi		3,1416	3
1150	Bhāskara II	3927 ⁄ 1250 och 754 ⁄ 240	3,1416	3
1220	Fibonacci		3,141818	3
1320	Zhao Youqin		3,141592	6

1400–1949

Datum	WHO	Notera	Decimaler ( världsrekord i fetstil )
Alla poster från 1400 och framåt anges som antal korrekta decimaler .
1400	Madhava av Sangamagrama	Upptäckte den oändliga potensseriens expansion av π , nu känd som Leibniz-formeln för pi	10
1424	Jamshīd al-Kāshī		16
1573	Valentinus Otho	355 ⁄ 113	6
1579	François Viète		9
1593	Adriaan van Roomen		15
1596	Ludolph van Ceulen		20
1615			32
1621	Willebrord Snell (Snellius)	Elev till Van Ceulen	35
1630	Christoph Grienberger		38
1654	Christiaan Huygens	Använde en geometrisk metod som motsvarar Richardsons extrapolering	10
1665	Isaac Newton		16
1681	Takakazu Seki		11 16
1699	Abraham Sharp	Beräknade pi till 72 siffror, men alla stämde inte	71
1706	John Machin		100
1706	William Jones	Introducerade den grekiska bokstaven ' π '
1719	Thomas Fantet de Lagny	Beräknade 127 decimaler, men alla stämde inte	112
1722	Toshikiyo Kamata		24
1722	Katahiro Takebe		41
1739	Yoshisuke Matsunaga		51
1748	Leonhard Euler	Använde den grekiska bokstaven ' π ' i sin bok Introductio in Analysin Infinitorum och försäkrade dess popularitet.
1761	Johann Heinrich Lambert	Bevisat att π är irrationell
1775	Euler	Påpekade möjligheten att π kan vara transcendental
1789	Jurij Vega	Beräknade 140 decimaler, men alla stämde inte	126
1794	Adrien-Marie Legendre	Visade att π 2 (och därmed π ) är irrationell, och nämnde möjligheten att π kan vara transcendental.
Sent 1700-tal	Anonymt manuskript	Dyker upp på Radcliffe Library, i Oxford, England, upptäckt av FX von Zach, vilket ger värdet av pi till 154 siffror, varav 152 var korrekta	152
1824	William Rutherford	Beräknade 208 decimaler, men alla stämde inte	152
1844	Zacharias Dase och Strassnitzky	Beräknade 205 decimaler, men alla stämde inte	200
1847	Thomas Clausen	Beräknade 250 decimaler, men alla stämde inte	248
1853	Lehmann		261
1853	Rutherford		440
1853	William Shanks	Utökade sin beräkning till 707 decimaler 1873, men ett fel som introducerades i början av hans nya beräkning gjorde alla efterföljande siffror felaktiga (felet upptäcktes av DF Ferguson 1946).	527
1882	Ferdinand von Lindemann	Bevisat att π är transcendental ( Lindemann–Weierstrass sats )
1897	USA:s delstat Indiana	Kom nära att lagstifta värdet 3,2 (bland annat) för π . Husets proposition nr 246 antogs enhälligt. Lagförslaget stannade i delstatssenaten på grund av ett förslag på möjliga kommersiella motiv som involverade publicering av en lärobok.	0
1910	Srinivasa Ramanujan	Hittade flera snabbt konvergerande oändliga serier av π , som kan beräkna 8 decimaler av π med varje term i serien. Sedan 1980-talet har hans serier blivit grunden för de snabbaste algoritmerna som för närvarande används av Yasumasa Kanada och Chudnovsky-bröderna för att beräkna π .
1946	DF Ferguson	De flesta siffror någonsin beräknade för hand.	620
1947	Ivan Niven	Gav ett mycket elementärt bevis på att π är irrationellt
januari 1947	DF Ferguson	Använde en skrivbordsräknare	710
september 1947	DF Ferguson	Skrivbordsräknare	808
1949	Levi B. Smith och John Wrench	Använde en skrivbordsräknare	1 120

1949–2009

Datum	WHO	Genomförande	Tid	Decimaler ( världsrekord i fetstil )
Alla rekord från 1949 och framåt beräknades med elektroniska datorer.
1949	GW Reitwiesner et al.	Den första som använde en elektronisk dator ( ENIAC ) för att beräkna π	70 timmar	2 037
1953	Kurt Mahler	Visade att π inte är ett Liouville-tal
1954	SC Nicholson & J. Jeenel	Använder NORC	13 minuter	3 093
1957	George E. Felton	Ferranti Pegasus-dator (London), beräknade 10 021 siffror, men alla var inte korrekta	33 timmar	7 480
januari 1958	Francois Genuys	IBM 704	1,7 timmar	10 000
maj 1958	George E. Felton	Pegasus dator (London)	33 timmar	10 021
1959	Francois Genuys	IBM 704 (Paris)	4,3 timmar	16,167
1961	Daniel Shanks och John Wrench	IBM 7090 (New York)	8,7 timmar	100 265
1961	JM Gerard	IBM 7090 (London)	39 minuter	20 000
1966	Jean Guilloud och J. Filliatre	IBM 7030 (Paris)	28 timmar	250 000
1967	Jean Guilloud och M. Dichampt	CDC 6600 (Paris)	28 timmar	500 000
1973	Jean Guilloud och Martine Bouyer	CDC 7600	23,3 timmar	1 001 250
1981	Kazunori Miyoshi och Yasumasa Kanada	FACOM M-200	137,3 timmar	2 000 036
1981	Jean Guilloud	Okänt		2 000 050
1982	Yoshiaki Tamura	MELCOM 900II	7.23 timmar	2,097,144
1982	Yoshiaki Tamura och Yasumasa Kanada	HITAC M-280H	2,9 timmar	4,194,288
1982	Yoshiaki Tamura och Yasumasa Kanada	HITAC M-280H	6,86 timmar	8,388,576
1983	Yasumasa Kanada , Sayaka Yoshino och Yoshiaki Tamura	HITAC M-280H		16,777,206
oktober 1983	Yasunori Ushiro och Yasumasa Kanada	HITAC S-810/20		10 013 395
oktober 1985	Bill Gosper	Symbolik 3670		17 526 200
januari 1986	David H. Bailey	CRAY-2		29,360,111
september 1986	Yasumasa Kanada , Yoshiaki Tamura	HITAC S-810/20		33,554,414
oktober 1986	Yasumasa Kanada , Yoshiaki Tamura	HITAC S-810/20		67,108,839
januari 1987	Yasumasa Kanada , Yoshiaki Tamura, Yoshinobu Kubo och andra	NEC SX-2		134 214 700
januari 1988	Yasumasa Kanada och Yoshiaki Tamura	HITAC S-820/80	5,95 timmar	201,326,551
maj 1989	Gregory V. Chudnovsky & David V. Chudnovsky	CRAY-2 & IBM 3090/VF		480 000 000
juni 1989	Gregory V. Chudnovsky & David V. Chudnovsky	IBM 3090		535,339,270
juli 1989	Yasumasa Kanada och Yoshiaki Tamura	HITAC S-820/80		536,870,898
augusti 1989	Gregory V. Chudnovsky & David V. Chudnovsky	IBM 3090		1 011 196 691
19 november 1989	Yasumasa Kanada och Yoshiaki Tamura	HITAC S-820/80		1 073 740 799
augusti 1991	Gregory V. Chudnovsky & David V. Chudnovsky	Hemmagjord parallelldator (detaljer okända, ej verifierade)		2 260 000 000
18 maj 1994	Gregory V. Chudnovsky & David V. Chudnovsky	Ny hemmagjord parallelldator (detaljer okända, ej verifierade)		4 044 000 000
26 juni 1995	Yasumasa Kanada och Daisuke Takahashi	HITAC S-3800/480 (dubbel CPU)		3 221 220 000
1995	Simon Plouffe	Hittar en formel som gör att den n: te hexadecimala siffran i pi kan beräknas utan att de föregående siffrorna beräknas.
28 augusti 1995	Yasumasa Kanada och Daisuke Takahashi	HITAC S-3800/480 (dubbel CPU)	56.74 timmar?	4 294 960 000
11 oktober 1995	Yasumasa Kanada och Daisuke Takahashi	HITAC S-3800/480 (dubbel CPU)	116.63 timmar	6 442 450 000
6 juli 1997	Yasumasa Kanada och Daisuke Takahashi	HITACHI SR2201 (1024 CPU)	29.05 timmar	51 539 600 000
5 april 1999	Yasumasa Kanada och Daisuke Takahashi	HITACHI SR8000 (64 av 128 noder)	32,9 timmar	68 719 470 000
20 september 1999	Yasumasa Kanada och Daisuke Takahashi	HITACHI SR8000/MPP (128 noder)	37.35 timmar	206 158 430 000
24 november 2002	Yasumasa Kanada & 9-mannalag	HITACHI SR8000/MPP (64 noder), Institutionen för informationsvetenskap vid University of Tokyo i Tokyo , Japan	600 timmar	1 241 100 000 000
29 april 2009	Daisuke Takahashi et al.	T2K Open Supercomputer (640 noder), enstaka nodhastighet är 147,2 gigaflops , datorminne är 13,5 terabyte , Gauss–Legendre-algoritm , Center for Computational Sciences vid University of Tsukuba i Tsukuba , Japan	29.09 timmar	2,576,980,377,524

2009 – nutid

Datum	WHO	Genomförande	Tid	Decimaler ( världsrekord i fetstil )
Alla poster från december 2009 och framåt beräknas och verifieras på servrar och/eller hemdatorer med kommersiellt tillgängliga delar .
31 december 2009	Fabrice Bellard	Core i7 CPU på 2,93 GHz 6 GiB (1) RAM 7,5 TB disklagring med fem 1,5 TB hårddiskar (Seagate Barracuda 7200.11-modell) 64-bitars Red Hat Fedora 10-distribution Beräkning av binära siffror: 103 dagar Verifiering av binära siffror: 13 dagar Konvertering till bas 10: 12 dagar Verifiering av omvandlingen: 3 dagar Verifiering av de binära siffrorna använde ett nätverk av 9 stationära datorer under 34 timmar, Chudnovsky algorithm , se för Bellards hemsida.	131 dagar	2 699 999 990 000
2 augusti 2010	Shigeru Kondo	använder y-cruncher av Alexander Yee Chudnovsky -algoritmen användes för huvudberäkning verifiering använde Bellard & BBP (Plouffe) formler på olika datorer; båda beräknade 32 hexadecimala siffror som slutar med 4,152,410,118,610. med 2× Intel Xeon X5680 @ 3,33 GHz – (12 fysiska kärnor, 24 hypertrådade) 96 GiB DDR3 @ 1066 MHz – (12× 8 GiB – 6 kanaler) – Samsung (M393B1K70BH1) 1 TB SATA II (startenhet) – Hitachi (HDS721010CLA332), 3× 2 TB SATA II (Store Pi Output) – Seagate (ST32000542AS) 16× 2 TB SATA II (Beräkning) – Seagate (ST32000641AS) Windows Server 2008 R2 Enterprise x64 Beräkning av binära siffror: 80 dagar Konvertering till bas 10: 8,2 dagar Verifiering av omvandlingen: 45,6 timmar Verifiering av binära siffror: 64 timmar (primär), 66 timmar (sekundär) Verifiering av de binära siffrorna gjordes samtidigt på två separata datorer under huvudberäkningen.	90 dagar	5 000 000 000 000
17 oktober 2011	Shigeru Kondo	använder y-cruncher av Alexander Yee Chudnovsky -algoritmen användes för huvudberäkning Verifiering med Bellard & BBP (Plouffe) formler: 1,86 dagar och 4,94 dagar	371 dagar	10 000 000 000 050
28 december 2013	Shigeru Kondo	använder y-cruncher av Alexander Yee med 2× Intel Xeon E5-2690 @ 2,9 GHz – (16 fysiska kärnor, 32 hypertrådade) 128 GiB DDR3 @ 1600 MHz – 8× 16 GiB – 8 kanaler Windows Server 2012 x64 Chudnovsky -algoritmen användes för huvudberäkning Verifiering med Bellards variant av BBP-formeln: 46 timmar	94 dagar	12 100 000 000 050
8 oktober 2014	Sandon Nash Van Ness "houkouonchi"	använder y-cruncher av Alexander Yee med 2× Xeon E5-4650L @ 2,6 GHz 192 GiB DDR3 @ 1333 MHz 24× 4 TB + 30× 3 TB Chudnovsky -algoritmen användes för huvudberäkning Verifiering med BBP-formeln: 182 timmar	208 dagar	13 300 000 000 000
11 november 2016	Peter Trueb	använder y-cruncher av Alexander Yee med 4× Xeon E7-8890 v3 @ 2,50 GHz (72 kärnor, 144 trådar) 1,25 TiB DDR4 20×6 TB Chudnovsky -algoritmen användes för huvudberäkning Verifiering med Bellards variant av BBP-formeln: 28 timmar	105 dagar	22 459 157 718 361 = ⌊ π e × 10 12 ⌋
14 mars 2019	Emma Haruka Iwao	använder y-cruncher v0.7.6 Beräkning: 1× n1-megamem-96 (96 vCPU, 1,4 TB) med 30 TB SSD Lagring: 24× n1-standard-16 (16 vCPU, 60 GB) med 10 TB SSD Chudnovsky -algoritmen användes för huvudberäkning Verifiering: 20 timmar med Bellards 7-term BBP-formel och 28 timmar med Plouffes 4-term BBP-formel	121 dagar	31 415 926 535 897 = ⌊ π × 10 13 ⌋
29 januari 2020	Timothy Mullican	använder y-cruncher v0.7.7 Beräkning: 4x Intel Xeon CPU E7-4880 v2 @ 2,50 GHz 320 GB DDR3 PC3-8500R ECC RAM 48× 6 TB hårddiskar (beräkning) + 47× LTO Ultrium 5 1,5 TB band (Checkpoint Backups) + 12× 4 TB hårddiskar (sifferlagring) Chudnovsky -algoritmen användes för huvudberäkning Verifiering: 17 timmar med Bellards 7-term BBP-formel , 24 timmar med Plouffes 4-term BBP-formel	303 dagar	50 000 000 000 000
14 augusti 2021	Team DAViS från University of Applied Sciences i Grisons	använder y-cruncher v0.7.8 Beräkning: AMD Epyc 7542 @ 2,9 GHz 1 TiB minne 38x 16 TB hårddiskar (av dessa används 34 för att byta och 4 används för lagring) Chudnovsky -algoritmen användes för huvudberäkning Verifiering: 34 timmar med Bellards 4-term BBP formel	108 dagar	62 831 853 071 796 = ⌊ 2 π × 10 13 ⌋
21 mars 2022	Emma Haruka Iwao	använder y-cruncher v0.7.8 Beräkning: n2-highmem-128 (128 vCPU och 864 GB RAM) Lagring: 663 TB Chudnovsky -algoritmen användes för huvudberäkning Verifiering: 12,6 timmar med BBP-formel	158 dagar	100 000 000 000 000

Se även

• Pi:s historia
• Approximationer av π

externa länkar

• Borwein, Jonathan, " The Life of Pi "
• Kanada Laboratory hemsida
• Stus Pi-sida
• Takahashis sida