Likhet (geometri)

För annan användning, se Likhet (disambiguation) och Likhetsomvandling (disambiguation) .

Liknande figurer

I euklidisk geometri är två objekt lika om de har samma form , eller om det ena har samma form som spegelbilden av det andra. Mer exakt kan den ena erhållas från den andra genom enhetlig skalning (förstoring eller förminskning), eventuellt med ytterligare translation , rotation och reflektion . Detta innebär att båda objekten kan skalas om, flyttas om och reflekteras så att de sammanfaller exakt med det andra objektet. Om två objekt är lika, är vart och ett kongruent med resultatet av en viss enhetlig skalning av det andra.

Översättning

Rotation

Reflexion

Skalning

Till exempel, alla cirklar liknar varandra, alla kvadrater liknar varandra och alla liksidiga trianglar liknar varandra. Å andra sidan, ellipser är inte alla lika varandra, rektanglar är inte alla lika varandra, och likbenta trianglar är inte alla lika varandra. Detta beror på att två ellipser kan ha olika förhållande mellan bredd och höjd, två rektanglar kan också ha olika förhållande mellan längd och bredd och två likbenta trianglar kan ha olika basvinklar.

Figurer som visas i samma färg är liknande

Om två vinklar i en triangel har mått lika med måtten på två vinklar i en annan triangel, så är trianglarna lika. Motsvarande sidor av liknande polygoner är i proportion, och motsvarande vinklar av liknande polygoner har samma mått.

Två kongruenta former är lika, med en skalfaktor på 1. Vissa skolböcker exkluderar dock specifikt kongruenta trianglar från deras definition av liknande trianglar genom att insistera på att storlekarna måste vara olika om trianglarna ska kvalificera sig som lika.

Liknande trianglar

Två trianglar, △ ABC och △ A′B′C′ är lika om och endast om motsvarande vinklar har samma mått: detta innebär att de är lika om och endast om längden på motsvarande sidor är proportionella . Det kan visas att två trianglar med kongruenta vinklar ( likkantiga trianglar ) är lika, det vill säga att motsvarande sidor kan bevisas vara proportionella. Detta är känt som AAA likhetsteoremet. Observera att "AAA" är ett minnesmärke: var och en av de tre A:en hänvisar till en "vinkel". På grund av detta teorem förenklar flera författare definitionen av liknande trianglar för att bara kräva att motsvarande tre vinklar är kongruenta.

Det finns flera kriterier som var och en är nödvändig och tillräcklig för att två trianglar ska vara lika:

• Alla två par av vinklar är kongruenta, vilket i euklidisk geometri innebär att alla tre vinklarna är kongruenta:

Om ∠ BAC är lika i mått med ∠ B′A′C′ och ∠ ABC är lika i mått med ∠ A′B′C ′ , då innebär detta att ∠ ACB är lika i mått med ∠ A′C′B′ och trianglarna är lika.

• Alla motsvarande sidor är proportionella:

AB / A′B′ = BC / B′C′ = AC / A′C′ . Detta motsvarar att säga att en triangel (eller dess spegelbild) är en förstoring av den andra.

• Alla två par av sidor är proportionella, och vinklarna som ingår mellan dessa sidor är kongruenta:

AB / A′B′ = BC / B′C′ och ∠ ABC är lika i mått med ∠ A′B′C′ .

Detta är känt som SAS likhetskriteriet. "SAS" är en mnemonik: var och en av de två S:en hänvisar till en "sida"; A hänvisar till en "vinkel" mellan de två sidorna.

Symboliskt skriver vi likheten och olikheten mellan två trianglar △ ABC och △ A′B′C′ enligt följande:

$ABC\sim A'B'C'$

$ABC\nsim A'B'C'$

Det finns flera elementära resultat om liknande trianglar i euklidisk geometri:

• Alla två liksidiga trianglar är lika.
• Två trianglar, båda liknar en tredje triangel, liknar varandra ( transitivitet av likhet av trianglar).
• Motsvarande höjder av liknande trianglar har samma förhållande som motsvarande sidor.
• Två räta trianglar är lika om hypotenusan och en annan sida har längder i samma förhållande. Det finns flera likvärdiga förhållanden i det här fallet, som att de räta trianglarna har en spetsig vinkel av samma mått, eller att längden på benen (sidorna) är i samma proportion.

Med en triangel △ ABC och ett linjeavsnitt DE kan man med linjal och kompass hitta en punkt F så att △ ABC ∼ △ DEF . Påståendet att punkt F som uppfyller detta villkor existerar är Wallis postulat och är logiskt ekvivalent med Euklids parallellpostulat . I hyperbolisk geometri (där Wallis postulat är falskt) är liknande trianglar kongruenta.

I den axiomatiska behandlingen av euklidisk geometri som ges av George David Birkhoff (se Birkhoffs axiom ) användes SAS-likhetskriteriet ovan för att ersätta både Euklids parallellpostulat och SAS-axiomet som möjliggjorde den dramatiska förkortningen av Hilberts axiom .

Liknande trianglar utgör grunden för många syntetiska (utan användning av koordinater) bevis i euklidisk geometri. Bland de elementära resultaten som kan bevisas på detta sätt är: vinkelbisetorsatsen , den geometriska medelsatsen , Cevas sats , Menelaos sats och Pythagoras sats . Liknande trianglar utgör också grunden för rätvinklig trigonometri .

Andra liknande polygoner

Liknande rektanglar

Begreppet likhet sträcker sig till polygoner med fler än tre sidor. Givet två liknande polygoner är motsvarande sidor tagna i samma sekvens (även om medurs för en polygon och moturs för den andra) proportionella och motsvarande vinklar tagna i samma sekvens är lika i mått. Emellertid är proportionalitet av motsvarande sidor inte i sig tillräckligt för att bevisa likhet för polygoner bortom trianglar (annars skulle till exempel alla romber vara lika). Likalikhet mellan alla vinklar i följd är inte tillräckligt för att garantera likhet (annars skulle alla rektanglar vara lika). Ett tillräckligt villkor för likhet mellan polygoner är att motsvarande sidor och diagonaler är proportionella.

För givet n är alla vanliga n -goner lika.

Liknande kurvor

Flera typer av kurvor har egenskapen att alla exempel av den typen liknar varandra. Dessa inkluderar:

• Linjer (vilka som helst två rader är till och med kongruenta )
• Linjesegment
• Cirklar
• Paraboler
• Hyperboler av en specifik excentricitet
• Ellipser av en specifik excentricitet
• Kontaktledningar
• Grafer över logaritmfunktionen för olika baser
• Grafer över exponentialfunktionen för olika baser
• Logaritmiska spiraler är självlika

I det euklidiska rymden

En likhet (även kallad likhetstransformation eller likhet ) av ett euklidiskt utrymme är en bijektion f från utrymmet till sig självt som multiplicerar alla avstånd med samma positiva reella tal r , så att vi för två punkter x och y har

$d(f(x),f(y))=r\,d(x,y),\,$

där " d ( x , y ) " är det euklidiska avståndet från x till y . Det skalära r har många namn i litteraturen inklusive; förhållandet mellan likhet , sträckningsfaktorn och likhetskoefficienten . När r = 1 kallas likheten en isometri ( stel transformation ). Två uppsättningar kallas liknande om den ena är bilden av den andra under en likhet.

Som en karta f : ℝ ⁿ → ℝ ⁿ , en likhet av förhållande r tar formen

$f(x)=rAx+t,$

där A ∈ O _n (ℝ) är en n × n ortogonal matris och t ∈ ℝ ⁿ är en translationsvektor.

Likheter bevarar plan, linjer, vinkelräthet, parallellitet, mittpunkter, olikheter mellan avstånd och linjesegment. Likheter bevarar vinklar men bevarar inte nödvändigtvis orientering, direkta liknelser bevarar orientering och motsatta liknelser ändrar den.

Likheterna i det euklidiska rummet bildar en grupp under kompositionens funktion som kallas likhetsgruppen S . De direkta likheterna bildar en normal undergrupp av S och den euklidiska gruppen E ( n ) av isometrier bildar också en normal undergrupp. Likhetsgruppen S är i sig en undergrupp till den affina gruppen , så varje likhet är en affin transformation .

Man kan se det euklidiska planet som det komplexa planet , det vill säga som ett tvådimensionellt utrymme över det verkliga . 2D-likhetstransformationerna kan sedan uttryckas i termer av komplex aritmetik och ges av f ( z ) = az + b (direkta likheter) och f ( z ) = a z + b (motsatta likheter), där a och b är komplexa siffror, a ≠ 0 . När | en | = 1 , dessa likheter är isometrier.

Ytförhållande och volymförhållande

Tessellationen av den stora triangeln visar att den liknar den lilla triangeln med ytförhållandet 5. Likhetsförhållandet är 5/ h = h 1 = √ 5 / . Detta kan användas för att konstruera en icke-periodisk oändlig plattsättning .

Huvudartikel: Square–cube law

Förhållandet mellan ytorna för liknande figurer är lika med kvadraten på förhållandet mellan motsvarande längder av dessa figurer (till exempel när sidan av en kvadrat eller radien på en cirkel multipliceras med tre, multipliceras dess area med nio — dvs med tre i kvadrat). Höjderna för liknande trianglar är i samma förhållande som motsvarande sidor. Om en triangel har en sida av längden b och en höjd ritad till den sidan av längden h så kommer en liknande triangel med motsvarande sida av längden kb att ha en höjd ritad till den sidan av längden kh . Arean av den första triangeln är, A = 1 / 2 bh , medan arean av den liknande triangeln kommer att vara A′ = 1 / 2 ( kb )( kh ) = k ² A . Liknande figurer som kan delas upp i liknande trianglar kommer att ha områden relaterade på samma sätt. Sambandet gäller även för siffror som inte är korrigerbara.

Förhållandet mellan volymerna för liknande figurer är lika med kuben för förhållandet mellan motsvarande längder av dessa figurer (till exempel när kanten på en kub eller radien på en sfär multipliceras med tre, multipliceras dess volym med 27 — dvs med tre kuber).

Galileos kvadrat-kub lag gäller liknande fasta ämnen. Om förhållandet av likhet (förhållandet mellan motsvarande sidor) mellan de fasta ämnena är k , så kommer förhållandet mellan ytareor av de fasta ämnena att vara k ² , medan förhållandet mellan volymer kommer att vara k ³ .

Likhet med ett centrum

Exempel där varje likhet sammansatt med sig själv flera gånger i följd har ett centrum i mitten av en vanlig polygon som den krymper.

Exempel på direkt likhet mellan centrum S sönderdelat till en rotation av 135° vinkel och en homotetitet som halverar områden .

Exempel på direkta likheter som har var och en ett centrum .

Om en likhet har exakt en invariant punkt : en punkt som likheten behåller oförändrad, så kallas denna enda punkt " centrum " av likheten.

På den första bilden under titeln, till vänster, krymper en eller annan likhet en regelbunden polygon till en koncentrisk , vars hörn är var och en på en sida av den föregående polygonen. Denna rotationsreduktion upprepas , så den initiala polygonen förlängs till en avgrund av vanliga polygoner. Likhetens centrum är det gemensamma centrumet för de successiva polygonerna . Ett rött segment förenar en vertex av den initiala polygonen till dess bild under likheten, följt av ett rött segment som går till följande bild av vertex, och så vidare för att bilda en spiral . I själva verket kan vi se mer än tre direkta likheter på denna första bild, eftersom varje vanlig polygon är invariant under vissa direkta likheter, närmare bestämt vissa rotationer vars centrum är polygonens centrum, och en sammansättning av direkta likheter är också en direkt likhet. Till exempel ser vi bilden av den initiala reguljära femhörningen under en homotet med negativt ${\text{ratio }}-k,\,$ vilket är en likhet av ±180° vinkel och ett positivt förhållande ${\text{lika med }}k.$

Under titeln till höger visar den andra bilden en likhet uppdelad i en rotation och en homoteti. Likhet och rotation har samma vinkel på +135 grader modulo 360 grader . Likhet och homoteti har samma förhållande $\displaystyle {\text{of }}\,{\frac {\sqrt {2}}{2}},}$ multiplikativ invers av $\, {\text{ratio }}{\sqrt {2}}\;$ ( kvadratroten ur 2 ) av den omvända likheten. Punkt S är det gemensamma centrumet för de tre transformationerna: rotation, homoteti och likhet. Till exempel punkt W är bilden av F under rotationen, och punkt T är bilden av W under homotetin, mer kortfattat T = H ( W ) = H ( R ( F )) = ( H ∘ R ) ( F ) = D ( F ) , genom att namnge $R,\;H{\text{ och }}D\,$ föregående rotation, homoteti och likhet, med " ${\text{“}}D\,{\text{” som “Direct”.}}\,$

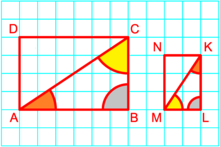
Denna direkta likhet som omvandlar triangeln EFA till triangeln ATB kan sönderdelas till en rotation och en homotetitet av samma centrum S på flera sätt. Till exempel, $D\,=\,R\,\circ \,H\,=\,H\,\circ \,R,$ den sista nedbrytningen är endast representeras på bilden. För att få $D$ kan vi också komponera i valfri ordning en rotation ${\text{ av }}-\,45^{\,\circ }$ vinkel och en homotet $\,{\text{av förhållandet }}\,{\frac {-\,{\sqrt {2}}\,}{2}}.$

Med ${\text{“}}M\,{\text{” som “Mirror”}}\,$ och ${\text {“}}I\,{\text{” som “Indirekt”,}}\,$ om $M\,$ är reflektionen med avseende på linje ( CW ), då ${\ displaystyle M\,\circ \,D\,=\,I\;}$ är den indirekta likheten som omvandlar segment [ BF ] ${\text{som }}D\,$ till segment [ CT ], men omvandlar punkt E till B och punkt A till A själv. Square ACBT är bilden av ${\displaystyle I\,{\text{ of ratio }}\;1\,/{\sqrt {2}}.\;} Punkt$ under likhet A är centrum för denna likhet eftersom varje punkt K som är invariant under den uppfyller $AK\,=\,AK/{\sqrt {2}},\;$ endast möjligt ${\text{if }}\,AK\, =\,0,\;$ annars skrivs $A\,=\,K.$

    Hur man konstruerar centrum S för direkt likhet $D$${\text{från kvadrat }}\,ABEF,\,$ hur man hittar punkt S centrum för en rotation av +135° vinkel som omvandlar stråle [ SE ) till stråle [ SA )? Detta är ett inskrivet vinkelproblem plus en fråga om orientering . Uppsättningen av punkter ${\displaystyle P\,{\text{ så att }}\;\angle \;{{\överhögerpil {PE}},\; {\overrightarrow {PA}}}\,=\,+\,135^{\,\circ }\,} är$ en cirkelbåge ${\overset {\frown }{EA}}\ ;$ som förenar E och A , av vilka de två radierna som leder till E och A bildar en central vinkel ${\text{of }}\;\;2\,(180^{\,\circ }\,-\,135^{\,\circ })\,=\,2\,\times \,45^{\,\circ }\,=\,90^{\,\circ }.\,$ Denna uppsättning punkter är den blå fjärdedelen av cirkeln av centrum F inuti kvadraten ABEF . På samma sätt är punkt S en medlem av den blå fjärdedelen av cirkeln av centrum T inuti kvadraten BCAT . Så punkt S är skärningspunkten för dessa två fjärdedelar av cirklar.

I allmänhet metriska utrymmen

Sierpiński triangel . Ett utrymme med självlikhet dimension log 3 / log 2 = log ₂ 3 , vilket är ungefär 1,58. (Från Hausdorff dimension .)

I ett allmänt metriskt utrymme ( X , d ) är en exakt likhet en funktion f från det metriska rummet X in i sig själv som multiplicerar alla avstånd med samma positiva skalära r , kallad fs kontraktionsfaktor, så att för två valfria punkter x och y vi har

$d(f(x),f(y))=rd(x,y).\,\,$

Svagare versioner av likhet skulle till exempel ha f vara en bi- Lipschitz -funktion och skalären r en gräns

$\lim {\frac {d(f(x),f(y))}{d(x,y)}}=r.$

Denna svagare version gäller när måtten är ett effektivt motstånd på en topologiskt självliknande uppsättning.

En självliknande delmängd av ett metriskt rum en ( X , d ) är en mängd K för vilken det finns ändlig uppsättning liknelser { f _s } _{s ∈ S} med kontraktionsfaktorer 0 ≤ r _s < 1 så att K är den unika kompakten delmängd av X för vilket

En självliknande uppsättning konstruerad med två liknelser z'=0.1[(4+i)z+4] och z'=0.1[(4+7i)z*+5-2i]

$\bigcup _{s\in S}f_{s}(K)=K.\,$

Dessa självliknande uppsättningar har ett självliknande mått μ ^D med dimension D som ges av formeln

$\sum _{s\in S}(r_{s})^{D}=1\,$

vilket ofta (men inte alltid) är lika med setets Hausdorff-dimension och packningsdimension . Om överlappningarna mellan f _s ( K ) är "små", har vi följande enkla formel för måttet:

$\mu ^{D}(f_{s_{1}}\circ f_{s_{2}}\circ \cdots \circ f_{s_{n}}(K))=(r_{s_{1 }}\cdot r_{s_{2}}\cdots r_{s_{n}})^{D}.\,$

Topologi

Inom topologi kan ett metriskt utrymme konstrueras genom att definiera en likhet istället för ett avstånd . Likheten är en funktion så att dess värde är större när två punkter är närmare (i motsats till avståndet, vilket är ett mått på olikhet : ju närmare punkterna, desto mindre avstånd).

Definitionen av likheten kan variera mellan författare, beroende på vilka egenskaper som önskas. De grundläggande gemensamma egenskaperna är

1. Positivt definierad:

   $\forall (a,b),S(a,b)\geq 0$

2. Huvudsaklig av likheten mellan ett element i sig själv ( autolikhet ):

   $S(a,b)\leq S(a,a)\quad {\text{and}}\quad \forall (a,b),S(a,b)=S(a, a)\Leftrightarrow a=b$

Fler egenskaper kan anropas, såsom reflektivitet ( $\forall (a,b)\ S(a,b)=S(b) ,a)$ ) eller finitet ( ${\displaystyle \forall (a,b)\ S(a,b)<\infty } )$ . Det övre värdet sätts ofta till 1 (vilket skapar en möjlighet för en sannolikhetstolkning av liknelsen).

Observera att, i den topologiska betydelsen som används här, är en likhet ett slags mått . Denna användning är inte densamma som likhetstransformationen av avsnitten § I det euklidiska utrymmet och § I allmänna metriska utrymmen i den här artikeln.

Självlikhet

Självlikhet betyder att ett mönster är icke-trivialt likt sig självt, t.ex. mängden {..., 0,5, 0,75, 1, 1,5, 2, 3, 4, 6, 8, 12, …} av tal av formen { 2 ⁱ , 3·2 ⁱ } där i sträcker sig över alla heltal. När denna mängd plottas på en logaritmisk skala har den endimensionell translationssymmetri : att addera eller subtrahera logaritmen för två till logaritmen för ett av dessa tal producerar logaritmen för ett annat av dessa tal. I själva den givna uppsättningen av tal motsvarar detta en likhetstransformation där talen multipliceras eller divideras med två.

Psykologi

Intuitionen för föreställningen om geometrisk likhet förekommer redan hos mänskliga barn, vilket kan ses i deras teckningar.

Se även

• Kongruens (geometri)
• Hamming-avstånd (sträng- eller sekvenslikhet)
• Helmerts förvandling
• Inversiv geometri
• Jaccard index
• Proportionalitet
• Grundläggande proportionalitetssats
• Semantisk likhet
• Likhetssökning
• Likhet (filosofi)
• Likhetsutrymme på numerisk taxonomi
• Homoeoid (skal av koncentriska, liknande ellipsoider)
• Lösning av trianglar

Anteckningar

•   Henderson, David W. ; Taimiņa, Daina (2005). Uppleva geometri/euklidisk och icke-euklidisk med historia (3:e upplagan). Pearson Prentice-Hall. ISBN 978-0-13-143748-7 .
•   Jacobs, Harold R. (1974). Geometri . WH Freeman och Co. ISBN 0-7167-0456-0 .
•   Pedoe, Dan (1988) [1970]. Geometri/En omfattande kurs . Dover. ISBN 0-486-65812-0 .
•   Sibley, Thomas Q. (1998). The Geometric Viewpoint/A Survey of Geometries . Addison-Wesley. ISBN 978-0-201-87450-1 .
•   Smart, James R. (1998). Modern Geometries (5:e upplagan). Brooks/Cole. ISBN 0-534-35188-3 .
•   Stahl, Saul (2003). Geometri/Från Euklid till Knots . Prentice-Hall. ISBN 978-0-13-032927-1 .
•   Venema, Gerard A. (2006). Geometrins grunder . Pearson Prentice-Hall. ISBN 978-0-13-143700-5 .
• Yale, Paul B. (1968). Geometri och symmetri . Holden-dagen.

Vidare läsning

•   Cederberg, Judith N. (2001) [1989]. "Kapitel 3.12: Likhetstransformationer". En kurs i moderna geometrier . Springer. s. 183–189. ISBN 0-387-98972-2 .
• Coxeter, HSM (1969) [1961]. "§5 Likhet i det euklidiska planet". s. 67–76. "§7 Isometri och likhet i det euklidiska rymden". s. 96–104. Introduktion till geometri . John Wiley & Sons .
• Ewald, Günter (1971). Geometri: En introduktion . Wadsworth Publishing . sid. 106, 181.
•   Martin, George E. (1982). "Kapitel 13: Likheter i planet". Transformation Geometry: En introduktion till symmetri . Springer. s. 136–146. ISBN 0-387-90636-3 .

externa länkar

• Animerad demonstration av liknande trianglar