Kerr-mått

Kerr -metriken eller Kerr-geometrin beskriver geometrin för tom rumtid runt ett roterande oladdat axiellt symmetriskt svart hål med en kvasisfärisk händelsehorisont . Kerr -metriken är en exakt lösning av Einsteins fältekvationer av allmän relativitet ; dessa ekvationer är mycket icke-linjära , vilket gör exakta lösningar mycket svåra att hitta.

Översikt

Kerr-metriken är en generalisering till en roterande kropp av Schwarzschild-metriken , upptäckt av Karl Schwarzschild 1915, som beskrev rumtidens geometri runt en oladdad, sfäriskt symmetrisk och icke-roterande kropp. Motsvarande lösning för en laddad , sfärisk, icke-roterande kropp, metriken Reissner–Nordström , upptäcktes kort därefter (1916–1918). Den exakta lösningen för ett oladdat, roterande svart hål, Kerr-metriken, förblev dock olöst till 1963, då det upptäcktes av Roy Kerr . Den naturliga förlängningen till ett laddat, roterande svart hål, Kerr-Newman-metriken , upptäcktes kort därefter 1965. Dessa fyra relaterade lösningar kan sammanfattas av följande tabell, där Q representerar kroppens elektriska laddning och J representerar dess rörelsemängd vid spinn. :

	Icke-roterande ( J = 0)	Roterande ( J ≠ 0)
Oladdat ( Q = 0)	Schwarzschild	Kerr
Laddad ( Q ≠ 0)	Reissner–Nordström	Kerr–Newman

Enligt Kerr-måttet bör en roterande kropp uppvisa bilddragning (även känd som Lense–Thirring-precession ), en distinkt förutsägelse av allmän relativitet. Den första mätningen av denna ramdragande effekt gjordes 2011 av Gravity Probe B- experimentet. Grovt sett förutsäger denna effekt att föremål som kommer nära en roterande massa kommer att fångas upp för att delta i dess rotation, inte på grund av någon applicerad kraft eller vridmoment som kan kännas, utan snarare på grund av den virvlande krökningen av rumtiden i sig associerad med roterande kroppar . I fallet med ett roterande svart hål, på tillräckligt nära avstånd, måste alla föremål – även ljusa – rotera med det svarta hålet; regionen där detta gäller kallas ergosfären .

Ljuset från avlägsna källor kan färdas runt händelsehorisonten flera gånger (om tillräckligt nära); skapa flera bilder av samma objekt . För en avlägsen betraktare minskar det skenbara vinkelräta avståndet mellan bilderna med en faktor på e ^{2 π} (ca 500). Snabbt snurrande svarta hål har dock mindre avstånd mellan flera bilder.

Roterande svarta hål har ytor där metriken verkar ha uppenbara singulariteter ; storleken och formen på dessa ytor beror på det svarta hålets massa och rörelsemängd . Den yttre ytan omsluter ergosfären och har en form som liknar en tillplattad sfär. Den inre ytan markerar händelsehorisonten ; objekt som passerar in i det inre av denna horisont kan aldrig mer kommunicera med världen utanför den horisonten. Ingendera ytan är dock en sann singularitet, eftersom deras skenbara singularitet kan elimineras i ett annat koordinatsystem . En liknande situation uppstår när man betraktar Schwarzschild-metriken som också verkar resultera i en singularitet vid r = r _s som delar upp utrymmet ovanför och under r _s i två frånkopplade fläckar; genom att använda en annan koordinattransformation kan man sedan relatera den utökade yttre lappen till den inre lappen (se Schwarzschild_metric#Singularities_and_black_holes ) - en sådan koordinattransformation eliminerar den skenbara singulariteten där de inre och yttre ytorna möts. Föremål mellan dessa två ytor måste rotera tillsammans med det roterande svarta hålet, som noterats ovan; denna funktion kan i princip användas för att extrahera energi från ett roterande svart hål, upp till dess invarianta massenergi , Mc ² .

LIGO-experimentet som först upptäckte gravitationsvågor, tillkännagav 2016, gav också den första direkta observationen av ett par Kerr-svarta hål.

Metrisk

Kerr-metriken uttrycks vanligtvis i en av två former, Boyer-Lindquist-formen och Kerr-Schild-formen. Det kan lätt härledas från Schwarzschild-metriken, med hjälp av Newman-Janis-algoritmen av Newman-Penrose-formalism (även känd som spin-koefficientformalism), Ernst-ekvation eller Ellipsoidkoordinattransformation.

Boyer–Lindquist koordinater

Huvudartikel: Boyer–Lindquist-koordinater

rumtidens geometri i närheten av en massa $M$ som roterar med rörelsemängd $J$ . Måttet (eller motsvarande dess linjeelement för korrekt tid ) i Boyer–Lindquist-koordinater är

${\begin{aligned}ds^{2}&=-c^{2} d\tau ^{2}\\&=-\left(1-{\frac {r_{\text{s}}r}{\Sigma }}\right)c^{2}dt^{2}+ {\frac {\Sigma }{\Delta }}dr^{2}+\Sigma d\theta ^{2}+\left(r^{2}+a^{2}+{\frac {r_{\ text{s}}ra^{2}}{\Sigma }}\sin ^{2}\theta \right)\sin ^{2}\theta \d\phi ^{2}-{\frac {2r_{ \text{s}}ra\sin ^{2}\theta }{\Sigma }}cdt\,d\phi \end{aligned}}$

 

 

 

 

()

där koordinaterna $r,\theta ,\phi$ är standard oblate sfäroidala koordinater , som är ekvivalenta med de kartesiska koordinaterna

$x={\sqrt {r^{2}+a^{2}}}\sin \theta \cos \phi$

 

 

 

 

()

$y={\sqrt {r^{2}+a^{2}}}\sin \theta \sin \phi$

 

 

 

 

()

$z=r\cos \theta ,$

 

 

 

 

()

där $r_{\text{s}}$ är Schwarzschild-radien

$r_{\text{s}}={\frac {2GM}{c^{2}}},$

 

 

 

 

()

och där för korthets skull längdskalorna $a,\Sigma$ och $\Delta$ har introducerats som

$a={\frac {J}{Mc}},$

 

 

 

 

()

$\Sigma =r^{2}+a^{2}\cos ^{2}\theta ,$

 

 

 

 

()

$\Delta =r^{2}-r_{\text{s}}r+a^{2}.$

 

 

 

 

()

En nyckelfunktion att notera i ovanstående mått är korsprodukttermen $dt\,d\phi .$ Detta innebär att det finns en koppling mellan tid och rörelse i det rotationsplan som försvinner när det svarta hålets rörelsemängd går till noll.

I den icke-relativistiska gränsen där $M$ (eller, ekvivalent, $r_{\text{s}}$ ) går till noll, blir Kerr-måttet det ortogonala måttet för de oblata sfäroidala koordinaterna

$g\mathop {\longrightarrow } _{M\to 0}-c^{2}dt^{2}+{\frac {\Sigma }{r^{2}+a^{2}}}dr^{2}+\Sigma d\ theta ^{2}+\left(r^{2}+a^{2}\right)\sin ^{2}\theta d\phi ^{2}$

 

 

 

 

()

Kerr–Schild-koordinater

Kerr-måttet kan uttryckas i "Kerr–Schild"-form , med hjälp av en speciell uppsättning kartesiska koordinater enligt följande. Dessa lösningar föreslogs av Kerr och Schild 1965.

$g_{\mu \nu }=\eta _{\mu \nu }+fk_{\mu }k_{\nu }\!$

 

 

 

 

()

$f={\frac {2GMr^{3}}{r^{4}+a^{2}z^{2}}}$

 

 

 

 

()

$\mathbf {k} =(k_ {x},k_{y},k_{z})=\left({\frac {rx+ay}{r^{2}+a^{2}}},{\frac {ry-ax}{ r^{2}+a^{2}}},{\frac {z}{r}}\right)$

 

 

 

 

()

$k_{0}=1.\!$

 

 

 

 

()

Lägg märke till att k är en enhet 3-vektor , vilket gör 4-vektorn till en nollvektor , med avseende på både g och η. Här M den konstanta massan för det snurrande föremålet, η är Minkowski-tensorn och a är en konstant rotationsparameter för det snurrande föremålet. Det är underförstått att vektorn ${\vec {a}}$ är riktad längs den positiva z-axeln. Kvantiteten r är inte radien, utan är snarare implicit definierad av

${\frac {x^{2}+y^{2}}{r^{2}+a^{2}}} +{\frac {z^{2}}{r^{2}}}=1$

 

 

 

 

()

Lägg märke till att kvantiteten r blir den vanliga radien R

$r\to R={\sqrt {x^{2}+y^{2}+z^{2}}}$

när rotationsparametern a närmar sig noll. I denna lösningsform väljs enheter så att ljusets hastighet är enhet ( c = 1). På stora avstånd från källan ( R ≫ a ) reduceras dessa ekvationer till Eddington–Finkelstein-formen av Schwarzschild-metriken .

I Kerr-Schild-formen av Kerr-metriken är bestämningsfaktorn för den metriska tensorn överallt lika med negativ, även nära källan.

Soliton koordinater

Eftersom Kerr-metriken (tillsammans med Kerr-NUT-metriken) är axiellt symmetrisk, kan den gjutas till en form som Belinski- Zakharov-transformen kan appliceras på. Detta antyder att Kerrs svarta hål har formen av gravitationssoliton .

Massa av rotationsenergi

Om hela rotationsenergin $E_{\rm {rot}}=c^{2}\left(M-M_{\rm {irr}} \right)$ av ett svart hål extraheras, till exempel med Penrose-processen kan den återstående massan inte krympa under den irreducerbara massan. Därför, om ett svart hål roterar med snurret $a=M$ , är dess totala massekvivalent $M$ högre med en faktor ${\sqrt {2}}$ i jämförelse med ett motsvarande Schwarzschild svart hål där $M$ är lika med $M_{\rm {irr}}$ . Anledningen till detta är att för att få en statisk kropp att snurra måste energi tillföras systemet. På grund av mass-energiekvivalensen har denna energi också en mass-ekvivalent, vilket adderar till systemets totala massenergi, $M$ .

Den totala massaekvivalenten $M$ (den graviterande massan) för kroppen (inklusive dess rotationsenergi ) och dess irreducerbara massa $M_{\rm {irr}}$ är relaterade till

$2M_{\rm {irr}}^{2}=M^{2}+{\sqrt {M^{4}-J^{2}c^{2}/G^{2}}} \Longrightarrow M^{2}={\frac {4M_{\rm {irr}}^{4}}{4M_{\rm {irr}}^{2}-a^{2}c^{4}/ G^{2}}}.$

Vågoperatör

Eftersom även en direkt kontroll av Kerr-måttet innebär besvärliga beräkningar, visas de kontravarianta komponenterna $g^{ik}$ av den metriska tensorn i Boyer-Lindquist-koordinater nedan i uttrycket för kvadraten av de fyra- gradientoperator : _

$stil {\mu \nu }{\frac {\partial }{\partial x^{\mu }}}{\frac {\partial }{\partial x^{\nu }}}=-{\frac {1} {c^{2}\Delta }}\left(r^{2}+a^{2}+{\frac {r_{\text{s}}ra^{2}}{\Sigma }}\sin ^{2}\theta \right)\left({\frac {\partial }{\partial t}}\right)^{2}-{\frac {2r_{\text{s}}ra}{c\ Sigma \Delta }}{\frac {\partial }{\partial \phi }}{\frac {\partial }{\partial {t}}}+{\frac {1}{\Delta \sin ^{2} \theta }}\left(1-{\frac {r_{\text{s}}r}{\Sigma }}\right)\left({\frac {\partial }{\partial \phi }}\right )^{2}+{\frac {\Delta }{\Sigma }}\left({\frac {\partial }{\partial r}}\right)^{2}+{\frac {1}{\ Sigma }}\left({\frac {\partial }{\partial \theta }}\right)^{2}}$

 

 

 

 

()

Ram drar

Vi kan skriva om Kerr-måttet () i följande form:

$c^{2}d\tau ^{2}=\left(g_{tt}-{\frac {g_{t\phi}^{2}}{g_{\phi \phi }}}\ höger)dt^{2}+g_{\mathrm {rr} }dr^{2}+g_{\theta \theta }d\theta ^{2}+g_{\phi \phi}\left(d\phi +{\frac {g_{t\phi}}{g_{\phi \phi }}}dt\right)^{2}.$

 

 

 

 

()

Detta mått är ekvivalent med en samroterande referensram som roterar med vinkelhastigheten Ω som beror på både radien r och kolituden θ , där Ω kallas Killing horizon .

$\Omega =-{\frac {g_{t\phi }}{g_{\phi \phi }}}={\frac {r_{\text{s}}rac}{\Sigma \left(r ^{2}+a^{2}\right)+r_{\text{s}}ra^{2}\sin ^{2}\theta }}.$

 

 

 

 

()

Således medbringas en tröghetsreferensram av den roterande centrala massan för att delta i den senares rotation; detta kallas frame-dragging och har testats experimentellt. Kvalitativt kan bilddragning ses som gravitationsanalogen till elektromagnetisk induktion. En "skridskoåkare", i omloppsbana över ekvatorn och roterande i vila med avseende på stjärnorna, sträcker ut sina armar. Armen som sträcks ut mot det svarta hålet kommer att vridas snurrande. Armen som sträcks bort från det svarta hålet kommer att vridas mot spinn. Hon kommer därför att snabbas upp rotationsmässigt, i en motroterande mening till det svarta hålet. Detta är motsatsen till vad som händer i vardagsupplevelsen. Om hon redan roterar med en viss hastighet när hon sträcker ut armarna, kommer tröghetseffekter och ramdragande effekter att balansera och hennes spin kommer inte att förändras. På grund av ekvivalensprincipen är gravitationseffekter lokalt omöjliga att skilja från tröghetseffekter, så denna rotationshastighet, med vilken ingenting händer när hon sträcker ut armarna, är hennes lokala referens för icke-rotation. Denna ram roterar med avseende på fixstjärnorna och motroterande med avseende på det svarta hålet. En användbar metafor är ett planetväxelsystem där det svarta hålet är solredskapet, skridskoåkaren är en planetväxel och det yttre universum är ringväxeln. Detta kan också tolkas genom Machs princip .

Viktiga ytor

Placering av horisonterna, ergosfärerna och ringsingulariteten för Kerr-rumtiden i kartesiska Kerr-Schild-koordinater.

Jämförelse av skuggan (svart) och de viktiga ytorna (vita) i ett svart hål. Spin-parametern a är animerad från 0 till M , medan den vänstra sidan av det svarta hålet roterar mot betraktaren.

Det finns flera viktiga ytor i Kerr-måttet (). Den inre ytan motsvarar en händelsehorisont som liknar den som observeras i Schwarzschild-metriken ; detta inträffar där den rent radiella komponenten g _rr hos metriken går till oändlighet. Att lösa andragradsekvationen 1 ⁄ g _rr = 0 ger lösningen:

$r_{\rm {H}}^{\pm }={\frac {r_{\text{s}}\pm {\sqrt { r_{\text{s}}^{2}-4a^{2}}}}{2}}$

vilket i naturliga enheter (som ger G = M = c = 1) förenklar till:

$r_{\rm {H}}^{\pm }=1\pm {\sqrt {1-a^{2}}}$

Medan i Schwarzschild-metriken är händelsehorisonten också den plats där den rent tidsmässiga komponenten g _tt av metriken ändrar tecken från positivt till negativt, i Kerr-metriken sker det på ett annat avstånd. Återigen lösa en andragradsekvation g _tt = 0 ger lösningen:

$r_{\rm {E}}^{\pm }={\frac {r_{\text{s}}\pm {\sqrt {r_{\text{s}}^{2}-4a^{2}\cos ^{2}\theta }}}{2}}$

eller i naturliga enheter:

$r_{\rm {E}}^{\pm }=1\pm {\sqrt {1-a^{2}\cos ^{2 }\theta }}$

På grund av termen cos ² θ i kvadratroten liknar denna yttre yta en tillplattad sfär som vidrör den inre ytan vid rotationsaxelns poler, där kolitud θ är lika med 0 eller π ; utrymmet mellan dessa två ytor kallas ergosfären . Inom denna volym är den rent tidsmässiga komponenten g _tt negativ, dvs fungerar som en rent rumslig metrisk komponent. Följaktligen måste partiklar inom denna ergosfär samrotera med den inre massan om de ska behålla sin tidsliknande karaktär. En rörlig partikel upplever en positiv riktig tid längs sin världslinje , sin väg genom rumtiden . Detta är dock omöjligt inom ergosfären, där g _tt är negativ, om inte partikeln samroterar runt den inre massan M med en vinkelhastighet på åtminstone Ω . Således kan ingen partikel röra sig i motsatt riktning mot centralmassans rotation inom ergosfären.

Liksom med händelsehorisonten i Schwarzschild-metriken , beror den skenbara singulariteten vid rH på valet av koordinater (dvs. det är en koordinatsingularitet ₎ . I själva verket kan rumtiden smidigt fortsätta genom den genom ett lämpligt val av koordinater. I sin tur är den yttre gränsen för ergosfären vid r _E inte singular i sig själv ens i Kerr-koordinater på grund av icke-noll $dtd\phi$ term.

Ergosphere och Penrose-processen

Huvudartikel: Penrose process

Ett svart hål i allmänhet är omgivet av en yta, som kallas händelsehorisonten och ligger vid Schwarzschild-radien för ett icke-roterande svart hål, där flykthastigheten är lika med ljusets hastighet. Inom denna yta kan ingen observatör/partikel hålla sig vid en konstant radie. Den tvingas falla inåt, så detta kallas ibland för den statiska gränsen .

Ett roterande svart hål har samma statiska gräns vid sin händelsehorisont men det finns en ytterligare yta utanför händelsehorisonten som kallas "ergoytan" som ges av

$(rM)^{2}=M^{2}-J^{2}\cos ^{2}\theta$

i Boyer–Lindquist coordinates , som intuitivt kan karakteriseras som sfären där "det omgivande utrymmets rotationshastighet" släpas med ljusets hastighet. Inom denna sfär är släpningen större än ljusets hastighet, och varje observatör/partikel tvingas samrotera.

Området utanför händelsehorisonten men innanför ytan där rotationshastigheten är ljusets hastighet kallas ergosfären ( från grekiska ergon som betyder arbete ). Partiklar som faller inom ergosfären tvingas rotera snabbare och får därmed energi. Eftersom de fortfarande är utanför händelsehorisonten kan de komma undan det svarta hålet. Nettoprocessen är att det roterande svarta hålet avger energiska partiklar på bekostnad av sin egen totala energi. Möjligheten att utvinna spinnenergi från ett roterande svart hål föreslogs först av matematikern Roger Penrose 1969 och kallas därför för Penroseprocessen . Roterande svarta hål i astrofysik är en potentiell källa till stora mängder energi och används för att förklara energiska fenomen, såsom gammastrålningskurar .

Funktioner hos Kerr-geometrin

Kerr-geometrin uppvisar många anmärkningsvärda egenskaper: den maximala analytiska förlängningen inkluderar en sekvens av asymptotiskt plana yttre regioner, var och en förknippad med en ergosfär , stationära gränsytor, händelsehorisonter , Cauchy-horisonter , stängda tidsliknande kurvor och en ringformad krökningssingularitet . Den geodetiska ekvationen kan lösas exakt i sluten form. Förutom två Killing-vektorfält (motsvarande tidsöversättning och axisymmetri ) tillåter Kerr-geometrin en anmärkningsvärd Killing-tensor . Det finns ett par huvudsakliga nollkongruenser (en ingående och en utgående ). Weyl -tensorn är algebraiskt speciell , i själva verket har den Petrov typ D. Den globala strukturen är känd. Topologiskt homotopitypen för Kerr-rumtiden enkelt karakteriseras som en linje med cirklar fästa vid varje heltalspunkt.

Observera att den inre Kerr-geometrin är instabil med avseende på störningar i det inre området. Denna instabilitet innebär att även om Kerr-metriken är axelsymmetrisk, kanske ett svart hål skapat genom gravitationskollaps inte är det. Denna instabilitet innebär också att många av egenskaperna hos Kerr-geometrin som beskrivs ovan kanske inte finns inuti ett sådant svart hål.

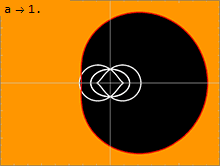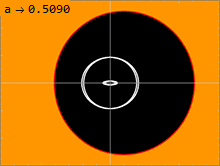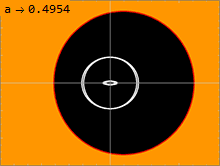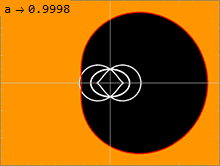
En yta på vilken ljus kan kretsa runt ett svart hål kallas en fotonsfär. Kerr-lösningen har oändligt många fotonsfärer , som ligger mellan en inre och en yttre. I den icke-roterande, Schwarzschild-lösningen, med a = 0, degenererar de inre och yttre fotonsfärerna, så att det bara finns en fotonsfär vid en enda radie. Ju större spinn ett svart hål har, desto längre från varandra rör sig de inre och yttre fotonsfärerna. En ljusstråle som rör sig i en riktning motsatt det svarta hålets spinn kommer att kretsa runt hålet vid den yttre fotonsfären. En ljusstråle som rör sig i samma riktning som det svarta hålets snurr kommer att kretsa runt den inre fotonsfären. Geodesik som kretsar runt med en viss rörelsemängd vinkelrätt mot det svarta hålets rotationsaxel kommer att kretsa kring fotonsfärer mellan dessa två ytterligheter. Eftersom rumtiden roterar, uppvisar sådana banor en precession, eftersom det finns en förskjutning i ${\displaystyle \phi \,}-$ variabeln efter att ha slutfört en period i ${\displaystyle \theta \,}-$ variabeln.

Banekvationer

Animation av en testpartikels bana runt ett snurrande svart hål. Vänster: ovanifrån, höger: sidovy.

En annan bana för en testmassa runt ett snurrande (Kerr) svart hål. Till skillnad från banor runt ett svart hål från Schwarzschild, är omloppsbanan inte begränsad till ett enda plan, utan kommer ergodiskt att fylla ett torusliknande område runt ekvatorn.

Rörelseekvationerna för testpartiklar i Kerrs rymdtid styrs av fyra rörelsekonstanter . Den första är den invarianta massan $\mu$ för testpartikeln, definierad av relationen

$$-\mu ^{2}=p^{\alpha }g_{\alpha \beta }p^{\beta },$$

där $p^{\alpha }$ är partikelns fyrmomentum . Dessutom finns det två rörelsekonstanter som ges av tidstranslationen och rotationssymmetrierna för Kerrs rumtid, energin $E$ och komponenten av det orbitala rörelsemängden parallellt med det svarta hålets spinn $L_{z}$ .

$$E=-p_{t},$$

och

$$L_{z}=p_{\phi }$$

Med hjälp av Hamilton–Jacobi-teorin visade Brandon Carter att det finns en fjärde rörelsekonstant, $Q$ , nu kallad Carter -konstanten . Det är relaterat till partikelns totala rörelsemängd och ges av

$$Q=p_{\theta }^{2}+\cos ^{2}\theta \left(a^{2}\left(\mu ^{2}-E^{2}\right)+ \left({\frac {L_{z}}{\sin \theta }}\right)^{2}\right).$$

Eftersom det finns fyra (oberoende) rörelsekonstanter för frihetsgrader, är rörelseekvationerna för en testpartikel i Kerrs rumtid integrerbara .

Med hjälp av dessa rörelsekonstanter kan banekvationerna för en testpartikel skrivas (med naturliga enheter av G = M = c = 1),

$${\begin{aligned}\Sigma {\frac {dr}{d\lambda }} &=\pm {\sqrt {R(r)}}\\\Sigma {\frac {d\theta }{d\lambda }}&=\pm {\sqrt {\Theta (\theta )}}\\ \Sigma {\frac {d\phi }{d\lambda }}&=-\left(aE-{\frac {L_{z}}{\sin ^{2}\theta }}\right)+{\ frac {a}{\Delta }}P(r)\\\Sigma {\frac {dt}{d\lambda }}&=-a\left(aE\sin ^{2}\theta -L_{z} \right)+{\frac {r^{2}+a^{2}}{\Delta }}P(r)\end{aligned}}$$

med

• $\Theta (\theta )=Q-\cos ^{2}\theta \left(a^{2}\left(\mu ^{2}-E^{2}\right)+{\frac {L_{z}^{2}}{\sin ^{2}\theta } }\höger)$
• $P(r)=E\left(r^{2}+a^{2}\right)-aL_{z}$
• $R(r)=P(r)^{2}-\Delta \left (\mu ^{2}r^{2}+(L_{z}-aE)^{2}+Q\höger)$

Där $\lambda$ är en affin parameter så att ${\frac {dx^{\alpha }}{d\lambda }}=p^{\alpha }$ . I synnerhet när ${\displaystyle \mu >0} är$ den affina parametern $\lambda$ relaterad till den korrekta tiden $\tau$ till $\lambda = \tau /\mu$ .

På grund av frame-dragging -effekten samroterar en noll-vinkelmomentumobservatör (ZAMO) med vinkelhastigheten $\Omega$ som definieras med avseende på bokhållarens koordinattid $t$ . Den lokala hastigheten $v$ för testpartikeln mäts i förhållande till en sond som samroterar med $\Omega$ . Gravitationstidsutvidgningen mellan en ZAMO vid fast $r$ och en stationär observatör långt bort från massan är

$${\frac {t}{\tau }}={\sqrt {\frac {\left(a^{2}+r^{2}\right)^{2}-a^{2}\ Delta \sin ^{2}\theta }{\Delta \ \Sigma }}}.$$

I kartesiska Kerr-Schild-koordinater är ekvationerna för en foton

$${\ddot {x}}+i{\ddot {y}}=4iMa{\frac {r}{\Sigma ^{2}}}W\left[{\dot { x}}+i{\dot {y}}-{\frac {x+iy}{r}}{\dot {r}}\right]-M(x+iy)\left({\frac {4r ^{2}}{\Sigma }}-1\right){\frac {Ca^{2}W^{2}}{r\Sigma ^{2}}}$$

$${\ddot {z}}=-Mz\left({\frac {4r^{2}}{\Sigma }}- 1\right){\frac {C}{r\Sigma ^{2}}}$$

där $C$ är analog med Carters konstant och $W$ är en användbar storhet

$$C=p_{\theta }^{2}+\left(aE\sin {\theta}-{\frac { L_{z}}{\sin {\theta }}}\right)^{2}$$

$$W={\dot {t}}-a\sin ^{2}{\theta }{\dot {\phi }}$$

Om vi ​​sätter $a=0$ återställs Schwarzschild -geodesiken .

Symmetrier

Gruppen av isometrier i Kerr-metriken är undergruppen av den tiodimensionella Poincaré-gruppen som tar singularitetens tvådimensionella lokus till sig själv. Den behåller tidsöversättningarna (en dimension) och rotationerna runt sin rotationsaxel (en dimension). Den har alltså två dimensioner. Liksom Poincaré-gruppen har den fyra sammankopplade komponenter: komponenten i identiteten; komponenten som vänder tid och longitud; komponenten som reflekteras genom ekvatorialplanet; och komponenten som gör båda.

Inom fysiken är symmetrier typiskt förknippade med bevarade rörelsekonstanter, i enlighet med Noethers sats . Som visas ovan har de geodetiska ekvationerna fyra bevarade storheter: en av dem kommer från definitionen av en geodetisk, och två av dem härrör från tidstranslationen och rotationssymmetrin för Kerr-geometrin. Den fjärde bevarade kvantiteten härrör inte från en symmetri i standardbemärkelsen och kallas vanligen för en dold symmetri.

Överextrema Kerr-lösningar

Placeringen av händelsehorisonten bestäms av den större roten av $\Delta =0$ . När $r_{\text{s}}/2<a$ (dvs. $GM^{2}<Jc$ ), finns det inga (verkligt värderade) ) lösningar på denna ekvation, och det finns ingen händelsehorisont. Utan några händelsehorisonter för att dölja det från resten av universum, upphör det svarta hålet att vara ett svart hål och kommer istället att vara en naken singularitet .

Kerr svarta hål som maskhål

Även om Kerr-lösningen verkar vara singular vid rötterna till Δ = 0, är ​​dessa faktiskt koordinatsingulariteter , och med ett lämpligt val av nya koordinater kan Kerr-lösningen smidigt utökas med värdena för $r$ motsvarande till dessa rötter. Den större av dessa rötter bestämmer platsen för händelsehorisonten, och den mindre bestämmer platsen för en Cauchy-horisont . En (framtidsriktad, tidsliknande) kurva kan börja i exteriören och passera genom händelsehorisonten. När den väl har passerat genom händelsehorisonten, $r$ -koordinaten nu som en tidskoordinat, så den måste minska tills kurvan passerar genom Cauchy-horisonten.

Regionen bortom Cauchy-horisonten har flera överraskande egenskaper. r $r$ -koordinaten beter sig återigen som en rumslig koordinat och kan variera fritt Det inre området har en reflektionssymmetri, så att en (framtidsriktad tidsliknande) kurva kan fortsätta längs en symmetrisk bana, som fortsätter genom en andra Cauchy-horisont, genom en andra händelsehorisont och ut i ett nytt yttre område som är isometrisk till den ursprungliga yttre regionen av Kerr-lösningen. Kurvan kan sedan fly till oändligheten i den nya regionen eller gå in i den framtida händelsehorisonten för den nya yttre regionen och upprepa processen. Detta andra yttre är ibland tänkt som ett annat universum. Å andra sidan, i Kerr-lösningen är singulariteten en ring , och kurvan kan passera genom mitten av denna ring. Regionen bortom tillåter stängda tidsliknande kurvor. Eftersom observatörernas och partiklarnas bana i allmän relativitet beskrivs av tidsliknande kurvor, är det möjligt för observatörer i denna region att återvända till sitt förflutna. Denna interiörlösning är sannolikt inte fysisk och betraktas som en rent matematisk artefakt.

Även om det förväntas att det yttre området av Kerr-lösningen är stabilt och att alla roterande svarta hål så småningom kommer att närma sig ett Kerr-mått, verkar den inre delen av lösningen vara instabil, ungefär som en penna som är balanserad på sin spets. Detta är relaterat till idén om kosmisk censur .

Relation till andra exakta lösningar

Kerr-geometrin är ett särskilt exempel på en stationär axiellt symmetrisk vakuumlösning till Einsteins fältekvation . Familjen av alla stationära axiellt symmetriska vakuumlösningar till Einsteins fältekvation är Ernst-vakuum.

Kerr-lösningen är också relaterad till olika icke-vakuumlösningar som modellerar svarta hål. Till exempel Kerr–Newman elektrovakuum ett (roterande) svart hål försett med en elektrisk laddning, medan Kerr–Vaidya nollstoft modellerar ett (roterande) hål med infallande elektromagnetisk strålning.

Specialfallet $a=0$ av Kerr-måttet ger Schwarzschild-måttet , som modellerar ett icke-roterande svart hål som är statiskt och sfäriskt symmetriskt , i Schwarzschild-koordinaterna . (I det här fallet försvinner varje Geroch-ögonblick utom massan.)

Det inre av Kerr-geometrin, eller snarare en del av den, är lokalt isometrisk till Chandrasekhar-Ferrari CPW-vakuumet, ett exempel på en kolliderande planvågsmodell. Detta är särskilt intressant, eftersom den globala strukturen för denna CPW-lösning skiljer sig helt från den för Kerr-geometrin, och i princip kan en experimentör hoppas kunna studera geometrin hos (den yttre delen av) Kerr-interiören genom att arrangera kollisionen av två lämpliga gravitationsplanvågor .

Flerpoliga moment

Varje asymptotiskt platt Ernst-vakuum kan karakteriseras genom att ge den oändliga sekvensen av relativistiska multipolmoment , varav de två första kan tolkas som massan och rörelsemängden för fältets källa. Det finns alternativa formuleringar av relativistiska multipolmoment på grund av Hansen, Thorne och Geroch, som visar sig överensstämma med varandra. De relativistiska multipolmomenten i Kerr-geometrin beräknades av Hansen; de visar sig vara

$M_{n}=M[ia]^{n}$

ger specialfallet med Schwarzschild-vakuum ( a = 0) " monopolpunktkällan " för allmän relativitet.

Weyl-multipolmoment uppstår genom att behandla en viss metrisk funktion (formellt motsvarar den Newtonska gravitationspotentialen) som visas i Weyl-Papapetrou-diagrammet för Ernst-familjen av alla stationära axisymmetriska vakuumlösningar med användning av standard euklidiska skalära multipolmoment . De skiljer sig från de ögonblick som beräknats av Hansen ovan. På sätt och vis karaktäriserar Weyl-momenten endast (indirekt) "massfördelningen" av en isolerad källa, och de visar sig bara bero på de relativistiska momenten med jämn ordning . I fallet med lösningar som är symmetriska över ekvatorialplanet försvinner de udda ordningens Weyl-moment. För Kerrs vakuumlösningar ges de första Weyl-momenten av

$a_{0}=M,\qquad a_{1}=0,\qquad a_{2}=M\left( {\frac {M^{2}}{3}}-a^{2}\right)$

I synnerhet ser vi att Schwarzschild-vakuumet har ett andra ordningens Weyl-moment som inte är noll, vilket motsvarar det faktum att "Weyl-monopolen" är Chazy-Curzon-vakuumlösningen, inte Schwarzschild-vakuumlösningen, som uppstår från den newtonska potentialen för en viss ändlig längd enhetlig densitet tunn stav .

I allmän relativitetsteori för svagt fält är det bekvämt att behandla isolerade källor med en annan typ av multipol, som generaliserar Weyl-momenten till massmultipolmoment och momentummultipolmoment , som kännetecknar fördelningen av källans massa respektive momentum . Dessa är multiindexerade storheter vars lämpligt symmetriserade och antisymmetriserade delar kan relateras till de verkliga och imaginära delarna av de relativistiska momenten för den fullständiga olinjära teorin på ett ganska komplicerat sätt.

Perez och Moreschi har gett en alternativ uppfattning om "monopollösningar" genom att utöka standarden NP-tetrad för Ernst-vakuum i potenser av r (den radiella koordinaten i Weyl–Papapetrou-diagrammet). Enligt denna formulering:

• den isolerade massmonopolkällan med noll rörelsemängd är Schwarzschild- vakuumfamiljen (en parameter),
• den isolerade massmonopolkällan med radiellt vinkelmoment är Taub-NUT- vakuumfamiljen (två parametrar; inte helt asymptotiskt platt),
• den isolerade massmonopolkällan med axiellt vinkelmoment är Kerr- vakuumfamiljen (två parametrar).

I denna mening är Kerr-vakuumerna de enklaste stationära axisymmetriska asymptotiskt platta vakuumlösningarna i allmän relativitet.

Öppna problem

Kerr-geometrin används ofta som en modell av ett roterande svart hål , men om lösningen endast anses vara giltig utanför någon kompakt region (med förbehåll för vissa restriktioner), bör den i princip kunna användas som en yttre lösning för att modellera gravitationsfältet runt ett roterande massivt föremål annat än ett svart hål som en neutronstjärna eller jorden. Detta fungerar mycket bra för det icke-roterande höljet, där Schwarzschild-vakuumexteriören kan matchas med en Schwarzschild-vätskeinredning , och faktiskt till mer allmänna statiska sfäriskt symmetriska perfekta vätskelösningar . Problemet med att hitta en roterande inre med perfekt vätska som kan matchas med en Kerr-exteriör, eller faktiskt till vilken asymptotiskt platt vakuumexteriörlösning som helst, har dock visat sig vara mycket svårt. I synnerhet är Wahlquist-vätskan , som en gång ansågs vara en kandidat för att matcha ett Kerr-exteriör, nu känt för att inte medge någon sådan matchning. För närvarande verkar det som om endast ungefärliga lösningar som modellerar långsamt roterande vätskekulor är kända (dessa är den relativistiska analogen av oblate sfäroidala bollar med massa som inte är noll och rörelsemängd men försvinnande högre multipolmoment). Emellertid närmar sig utsidan av Neugebauer-Meinel-skivan, en exakt dammlösning som modellerar en roterande tunn skiva, i ett begränsande fall $GM^{2}=cJ$ Kerr-geometrin. Fysiska tunndisklösningar som erhållits genom att identifiera delar av Kerr-rymdtiden är också kända.

Se även

• Schwarzschild-metrisk
• Kerr–Newman-metrik
• Reissner–Nordström metrisk
• Hartle–Thorne metrisk
• Spin-flip
• Kerr–Schild rymdtid
• Roterande svart hål

Vidare läsning

•   Wiltshire, David L.; Visser, Matt; Scott, Susan M. , red. (2009). The Kerr Spacetime: Roterande svarta hål i allmän relativitet . Cambridge: Cambridge University Press. ISBN 978-0-521-88512-6 .
•   Stephani, Hans; Kramer, Dietrich; MacCallum, Malcolm; Hoenselaers, Cornelius; Herlt, Eduard (2003). Exakta lösningar av Einsteins fältekvationer . Cambridge: Cambridge University Press. ISBN 978-0-521-46136-8 .
•   Meinel, Reinhard ; Ansorg, Marcus; Kleinwachter, Andreas; Neugebauer, Gernot; Petroff, David (2008). Relativistiska jämviktssiffror . Cambridge: Cambridge University Press. ISBN 978-0-521-86383-4 .
•   O'Neill, Barrett (1995). Kerrs svarta håls geometri . Wellesley, Massachusetts: AK Peters. ISBN 978-1-56881-019-5 .
•   D'Inverno, Ray (1992). Introduktion av Einsteins relativitet . Oxford: Clarendon Press. ISBN 978-0-19-859686-8 . Se kapitel 19 för en läsvärd introduktion på avancerad grundnivå.
•   Chandrasekhar, S. (1992). Den matematiska teorin om svarta hål . Oxford: Clarendon Press. ISBN 978-0-19-850370-5 . Se kapitel 6--10 för en mycket grundlig studie på avancerad forskarnivå.
•   Griffiths, JB (1991). Kolliderande planvågor i allmän relativitet . Oxford: Oxford University Press. ISBN 978-0-19-853209-5 . Se kapitel 13 för Chandrasekhar/Ferrari CPW-modellen.
•   Adler, Ronald; Bazin, Maurice; Schiffer, Menahem (1975). Introduktion till allmän relativitet (andra upplagan). New York: McGraw-Hill. ISBN 978-0-07-000423-8 . Se kapitel 7 .
• Penrose, R. (1968). ed C. de Witt och J. Wheeler (red.). Battelle Rencontres . WA Benjamin, New York. sid. 222.
• Perez, Alejandro; Moreschi, Osvaldo M. (2000). "Karakterisera exakta lösningar från asymptotiska fysiska begrepp". arXiv : gr-qc/0012100v1 . Karakterisering av tre standardfamiljer av vakuumlösningar enligt ovan.
•   Sotiriou, Thomas P.; Apostolatos, Theocharis A. (2004). "Korrigeringar och kommentarer om multipolmomenten av axisymmetriska elektrovakuumrumstider". Klass. Quantum Grav . 21 (24): 5727–5733. arXiv : gr-qc/0407064 . Bibcode : 2004CQGra..21.5727S . doi : 10.1088/0264-9381/21/24/003 . S2CID 16858122 . Ger de relativistiska multipolmomenten för Ernst-vakuum (plus de elektromagnetiska och gravitationsrelativistiska multipolmomenten för den laddade generaliseringen).
• Carter, B. (1971). "Axisymmetriskt svart hål har bara två frihetsgrader". Fysiska granskningsbrev . 26 (6): 331–333. Bibcode : 1971PhRvL..26..331C . doi : 10.1103/PhysRevLett.26.331 .
•   Wald, RM (1984). Allmän relativitet . Chicago: University of Chicago Press. s. 312–324. ISBN 978-0-226-87032-8 .
•   Kerr, RP; Schild, A. (2009). "Republicering av: En ny klass av vakuumlösningar av Einsteins fältekvationer". Allmän relativitet och gravitation . 41 (10): 2485–2499. Bibcode : 2009GReGr..41.2485K . doi : 10.1007/s10714-009-0857-z . S2CID 361088 .
• Krasiński, Andrzej; Verdaguer, Enric; Kerr, Roy Patrick (2009). "Redaktionell notering till: RP Kerr och A. Schild, En ny klass av vakuumlösningar av Einsteins fältekvationer" . Allmän relativitet och gravitation . 41 (10): 2469–2484. Bibcode : 2009GReGr..41.2469K . doi : 10.1007/s10714-009-0856-0 . "... Den här anteckningen är tänkt att vara en guide för de läsare som vill verifiera alla detaljer [om härledningen av Kerr-lösningen]..."