Världslinjen

"Worldline" omdirigerar hit. För det franska betaltjänstföretaget, se Worldline SA .

Världslinjen (eller världslinjen ) för ett objekt är den väg som ett objekt spårar i 4 - dimensionell rumtid . Det är ett viktigt begrepp inom modern fysik , och särskilt teoretisk fysik .

Begreppet "världslinje" skiljer sig från begrepp som en " omloppsbana " eller en " bana " (t.ex. en planets bana i rymden eller en bils bana på en väg) genom att inkludera dimensionen tid , och typiskt sett omfattar ett stort område av rymdtid där banor som är raka perceptuellt renderas som kurvor i rum-tid för att visa deras ( relativt ) mer absoluta positionstillstånd - för att avslöja arten av speciell relativitet eller gravitationsinteraktioner .

Idén om världslinjer uppstod av fysiker och pionjärer av Hermann Minkowski . Termen används nu oftast i samband med relativitetsteorier (dvs speciell relativitet och allmän relativitet) .

Användning i fysik

En världslinje för ett objekt (vanligtvis approximerad som en punkt i rymden, t.ex. en partikel eller observatör) är sekvensen av rymdtidshändelser som motsvarar objektets historia. En världslinje är en speciell typ av kurva i rumtiden. Nedan kommer en motsvarande definition att förklaras: En världslinje är en tidsliknande kurva i rumtiden. Varje punkt på en världslinje är en händelse som kan märkas med tiden och den rumsliga positionen för objektet vid den tiden.

Till exempel är jordens bana i rymden ungefär en cirkel, en tredimensionell (sluten) kurva i rymden: Jorden återvänder varje år till samma punkt i rymden i förhållande till solen. Däremot anländer den vid en annan (senare) tidpunkt. Jordens världslinje är därför spiralformad i rymdtiden (en kurva i en fyrdimensionell rymd) och återvänder inte till samma punkt .

Spacetime är samlingen av händelser , tillsammans med ett kontinuerligt och smidigt koordinatsystem som identifierar händelserna. Varje händelse kan märkas med fyra siffror: en tidskoordinat och tre rymdkoordinater; alltså rumstid är ett fyrdimensionellt rum. Den matematiska termen för rumtid är en fyrdimensionell mångfald (ett topologiskt rum som lokalt liknar det euklidiska rummet nära varje punkt). Konceptet kan även appliceras på ett högre dimensionellt utrymme. För enkla visualiseringar av fyra dimensioner undertrycks ofta två rymdkoordinater. En händelse representeras sedan av en punkt i ett Minkowski-diagram , vilket är ett plan som vanligtvis plottas med tidskoordinaten, säg $t$ , vertikalt, och rymdkoordinaten, säg $x$ , horisontellt. Som uttryckt av FR Harvey

En kurva M i [rymdtid] kallas en världslinje för en partikel om dess tangent är framtida tidsliknande vid varje punkt. Båglängdsparametern kallas korrekt tid och betecknas vanligtvis τ. Längden på M kallas partikelns rätta tid . Om världslinjen M är ett linjesegment, sägs partikeln vara i fritt fall .

En världslinje spårar vägen för en enda punkt i rymdtiden. Ett världsark är den analoga tvådimensionella ytan som spåras ut av en endimensionell linje (som en sträng) som färdas genom rumtiden. Världsarket av ett öppet snöre (med lösa ändar) är en remsa; att en sluten sträng (en slinga) liknar ett rör.

När objektet väl inte är ungefärligt som en punkt utan har utökad volym, spårar det inte en världslinje utan snarare ett världsrör.

Världslinjer som en metod för att beskriva händelser

Världslinje, världsark och världsvolym, eftersom de härrör från partiklar , strängar och braner .

En endimensionell linje eller kurva kan representeras av koordinaterna som en funktion av en parameter. Varje värde på parametern motsvarar en punkt i rymdtiden och om parametern varieras spåras en linje. Så i matematiska termer definieras en kurva av fyra koordinatfunktioner $x^{a}(\tau ),\;a=0,1,2,3$ (där $x^{0}$ vanligtvis betecknar tidskoordinaten) beroende på en parameter $\tau$ . Ett koordinatnät i rumtid är den uppsättning kurvor man får om tre av fyra koordinatfunktioner sätts till en konstant.

används termen världslinje informellt för vilken kurva som helst i rymdtiden. Denna terminologi orsakar förvirring. Mer korrekt är en världslinje en kurva i rumtiden som spårar (tids)historien för en partikel, observatör eller ett litet föremål. Man använder vanligtvis rätt tid för ett objekt eller en observatör som kurvparametern $\tau$ längs världslinjen.

Triviala exempel på rumtidskurvor

Tre olika världslinjer som representerar resor med olika konstanta fyra hastigheter. t är tid och x avstånd.

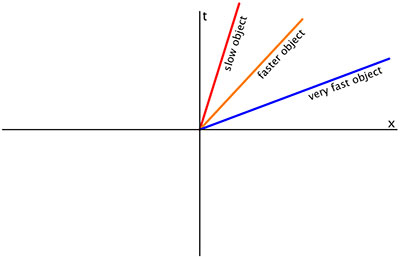
En kurva som består av ett horisontellt linjesegment (en linje vid konstant koordinattid), kan representera en stav i rymdtiden och skulle inte vara en världslinje i egentlig mening. Parametern spårar helt enkelt spöets längd.

En linje med konstant rymdkoordinat (en vertikal linje som använder konventionen ovan) kan representera en partikel i vila (eller en stationär observatör). En lutad linje representerar en partikel med konstant koordinathastighet (konstant förändring i rymdkoordinaten med ökande tidskoordinat). Ju mer linjen lutar från vertikalen, desto högre hastighet.

Två världslinjer som börjar separat och sedan korsar varandra, betecknar en kollision eller "möte". Två världslinjer som börjar vid samma händelse i rymdtiden, som var och en följer sin egen väg efteråt, kan representera t.ex. en partikels sönderfall till två andra eller emission av en partikel från en annan.

Världslinjer för en partikel och en observatör kan vara sammankopplade med en fotons världslinje (ljusets väg) och bilda ett diagram som visar emissionen av en foton från en partikel som sedan observeras av observatören (eller absorberas av en annan partikel). ).

Tangent vektor till en världslinje: fyra hastigheter

De fyra koordinatfunktionerna $x^{a}(\tau ),\;a=0,1,2,3$ som definierar en världslinje, är verkliga talfunktioner för en reell variabel $\tau$ och kan helt enkelt särskiljas med den vanliga kalkylen. Utan att det finns ett mått (detta är viktigt att inse) kan man föreställa sig skillnaden mellan en punkt $p$ på kurvan vid parametervärdet $\tau _{0}$ och en punkt på kurva lite (parameter $\tau _{0}+\Delta \tau$ ) längre bort. I gränsen ${\displaystyle \Delta \tau \to 0} ,$ definierar denna skillnad dividerat med ${\displaystyle \Delta \tau } en vektor,$ tangentvektorn för världslinjen i punkten $p$ . Det är en fyrdimensionell vektor, definierad i punkten $p$ . Den är associerad med objektets normala 3-dimensionella hastighet (men den är inte densamma) och kallas därför fyrhastighet ${\displaystyle {\vec {v}}} ,$ eller i komponenter:

$${\vec {v}} =\left(v^{0},v^{1},v^{2},v^{3}\right)=\left({\frac {dx^{0}}{d\tau }} \;,{\frac {dx^{1}}{d\tau }}\;,{\frac {dx^{2}}{d\tau }}\;,{\frac {dx^{3} }{d\tau }}\right)$$

så att derivatorna tas i punkten $p$ , så vid $\tau =\tau _{0}$ .

Alla kurvor genom punkt p har en tangentvektor, inte bara världslinjer. Summan av två vektorer är återigen en tangentvektor till någon annan kurva och detsamma gäller för att multiplicera med en skalär. Därför spänner alla tangentvektorer för en punkt p ett linjärt utrymme , benämnt tangentrymden vid punkt p. Om man till exempel tar ett 2-dimensionellt utrymme, som jordens (krökta) yta, skulle dess tangentrymd vid en specifik punkt vara den platta approximationen av det böjda utrymmet.

Världslinjer i speciell relativitet

Hittills har en världslinje (och begreppet tangentvektorer) beskrivits utan ett sätt att kvantifiera intervallet mellan händelser. Den grundläggande matematiken är som följer: Teorin om speciell relativitet sätter vissa begränsningar för möjliga världslinjer. I speciell relativitet är beskrivningen av rumtid begränsad till speciella koordinatsystem som inte accelererar (och alltså inte roterar heller), kallade tröghetskoordinatsystem . I sådana koordinatsystem ljusets hastighet konstant. Rymdtidens struktur bestäms av en bilinjär form η, som ger ett reellt tal för varje händelsepar. Den bilinjära formen kallas ibland för en rumstidsmetrik , men eftersom distinkta händelser ibland resulterar i ett nollvärde, till skillnad från mått i metriska rum i matematik, är den bilinjära formen inte ett matematiskt mått på rumtid.

Världslinjer av fritt fallande partiklar/objekt kallas geodetik . I speciell relativitet är dessa raka linjer i Minkowskis rymd .

Ofta väljs tidsenheterna så att ljusets hastighet representeras av linjer i en fast vinkel, vanligtvis vid 45 grader, som bildar en kon med den vertikala (tids)axeln. I allmänhet kan användbara kurvor i rymdtid vara av tre typer (de andra typerna skulle vara delvis en, delvis en annan typ):

• ljusliknande kurvor, som vid varje punkt har ljusets hastighet. De bildar en kon i rumtiden och delar den i två delar. Konen är tredimensionell i rumtid, visas som en linje i ritningar med två dimensioner undertryckta, och som en kon i ritningar med en rumslig dimension undertryckt.

Ett exempel på en ljuskon , den tredimensionella ytan av alla möjliga ljusstrålar som anländer till och avgår från en punkt i rumtiden. Här är det avbildat med en rumslig dimension undertryckt.

De momentant samtidigt rörliga tröghetsramarna längs banan ("världslinjen") för en snabbt accelererande observatör (mitten). Den vertikala riktningen indikerar tid, medan den horisontella indikerar avstånd, den streckade linjen är observatörens rumstid . De små prickarna är specifika händelser i rumtiden. Lägg märke till hur den tillfälligt rörliga tröghetsramen ändras när observatören accelererar.

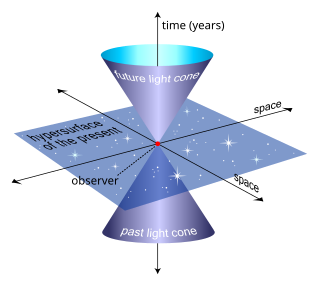
• tidsliknande kurvor, med en hastighet som är mindre än ljusets hastighet. Dessa kurvor måste falla inom en kon som definieras av ljusliknande kurvor. I vår definition ovan: världslinjer är tidsliknande kurvor i rumtid .
• rymdliknande kurvor som faller utanför ljuskäglan. Sådana kurvor kan till exempel beskriva längden på ett fysiskt föremål. En cylinders omkrets och längden på en stång är rymdliknande kurvor.

Vid en given händelse på en världslinje är rumtiden ( Minkowski space ) uppdelad i tre delar.

• Framtiden för den givna händelsen bildas av alla händelser som kan nås genom tidsliknande kurvor som ligger inom den framtida ljuskäglan.
• Det förflutna för den givna händelsen bildas av alla händelser som kan påverka händelsen (det vill säga som kan kopplas samman med världslinjer inom den förflutna ljuskonen till den givna händelsen).
  • Ljuskonen vid den givna händelsen bildas av alla händelser som genom ljusstrålar kan kopplas samman med händelsen . När vi observerar himlen på natten ser vi i princip bara den förflutna ljuskäglan under hela rumtiden.
• På andra ställen finns området mellan de två ljuskottarna. Punkter hos en observatör på andra ställen är otillgängliga för dem; endast punkter i det förflutna kan skicka signaler till observatören. Med vanlig laboratorieerfarenhet, med vanliga enheter och mätmetoder, kan det tyckas att vi tittar på nuet, men i själva verket finns det alltid en fördröjningstid för ljuset att fortplanta sig. Vi ser till exempel solen som den var för cirka 8 minuter sedan, inte som den är "just nu". Till skillnad från nutiden i galileisk/newtonsk teori är den andra platsen tjock; det är inte en 3-dimensionell volym utan är istället en 4-dimensionell rumstidsregion.
  • Inkluderat i "annanstans" är det samtidiga hyperplanet , som definieras för en given observatör av ett utrymme som är hyperboliskt-ortogonalt mot deras världslinje. Det är verkligen tredimensionellt, även om det skulle vara ett 2-plan i diagrammet eftersom vi var tvungna att kasta bort en dimension för att göra en begriplig bild. Även om ljuskäglarna är desamma för alla observatörer vid en given rumtidshändelse, har olika observatörer, med olika hastigheter men sammanfallande vid händelsen (punkten) i rymdtiden, världslinjer som korsar varandra i en vinkel som bestäms av deras relativa hastigheter, och sålunda har de olika samtidiga hyperplan.
  • Nutiden betyder ofta den enda rumtidshändelse som övervägs .

Samtidigt hyperplan

Eftersom en världslinje $w(\tau )\in R^{4}$ bestämmer en hastighet 4-vektor $v={\frac {dw} {d\tau }}$ som är tidsliknande, Minkowski-formen $\eta (v,x)$ bestämmer en linjär funktion $R^{4}\ högerpil R$ med $x\mapsto \eta (v,x).$ Låt N vara nollrummet för denna linjära funktion. Då kallas N det samtidiga hyperplanet med avseende på v . Relativiteten för samtidighet är ett påstående att N beror på v . N är faktiskt det ortogonala komplementet av v med avseende på η. När två världslinjer u och w är relaterade till ${\frac {du}{d\tau }}={\frac {dw}{d\tau }},$ sedan delar de samma samtidiga hyperplan. Detta hyperplan existerar matematiskt, men fysiska relationer i relativitetsteorien involverar förflyttning av information genom ljus. Till exempel kan den traditionella elektrostatiska kraften som beskrivs av Coulombs lag avbildas i ett simultant hyperplan, men relativistiska relationer mellan laddning och kraft involverar retarderade potentialer .

Världslinjer i allmän relativitet

Användningen av världslinjer i allmän relativitetsteori är i grunden densamma som i speciell relativitetsteori , med skillnaden att rumtiden kan krökas . Det finns ett mått och dess dynamik bestäms av Einsteins fältekvationer och är beroende av mass-energifördelningen i rumtiden. Återigen definierar måttet ljusliknande (null), rumsliknande och tidsliknande kurvor. Dessutom, i allmän relativitetsteori, är världslinjer tidsliknande kurvor i rumtid, där tidsliknande kurvor faller inom ljuskonen. En ljuskon lutar dock inte nödvändigtvis 45 grader mot tidsaxeln. allmänna relativitetsteoriens koordinatfrihet ( diffeomorfisminvarians) . Vilken tidsliknande kurva som helst tillåter en kommande observatör vars "tidsaxel" motsvarar den kurvan, och eftersom ingen observatör är privilegierad kan vi alltid hitta ett lokalt koordinatsystem där ljuskoner lutar 45 grader mot tidsaxeln. Se även till exempel Eddington-Finkelstein-koordinater .

Världslinjer av fritt fallande partiklar eller föremål (som planeter runt solen eller en astronaut i rymden) kallas geodetik .

Världslinjer i kvantfältteori

Kvantfältteori, det ramverk inom vilket all modern partikelfysik beskrivs, brukar beskrivas som en teori om kvantiserade fält. Men, även om det inte är allmänt uppskattat, har det varit känt sedan Feynman att många kvantfältsteorier på motsvarande sätt kan beskrivas i termer av världslinjer. Världslinjeformuleringen av kvantfältteorin har visat sig särskilt fruktbar för olika beräkningar i mätteorier och för att beskriva icke-linjära effekter av elektromagnetiska fält.

Världslinjer i litteraturen

1884 skrev CH Hinton en essä "Vad är den fjärde dimensionen?", som han publicerade som en vetenskaplig romans . Han skrev

Varför skulle då inte de fyrdimensionella varelserna vara vi själva, och våra successiva tillstånd passerar dem genom det tredimensionella utrymme till vilket vårt medvetande är begränsat.

En populär beskrivning av mänskliga världslinjer gavs av JC Fields vid University of Toronto under relativitetsteoriets tidiga dagar. Som beskrivs av Torontos advokat Norman Robertson:

Jag minns att [Fields] föreläste vid en av lördagskvällens föreläsningar på Royal Canadian Institute . Det annonserades som en "matematisk fantasi" - och det var det! Innehållet i övningen var som följer: Han postulerade att, från och med hans födelse, hade varje människa någon form av andlig aura med en lång filament eller tråd fäst, som reste bakom honom under hela hans liv. Han fortsatte sedan i fantasin för att beskriva den komplicerade förvecklingen varje individ blev involverad i sin relation till andra individer, och jämförde ungdomens enkla förvecklingar med de komplicerade knutar som utvecklas senare i livet.

Kurt Vonnegut beskriver i sin roman Slaughterhouse-Five världslinjerna för stjärnor och människor:

"Billy Pilgrim säger att universum inte ser ut som en massa ljusa små prickar för varelserna från Tralfamadore. Varelserna kan se var varje stjärna har varit och vart den är på väg, så att himlen fylls med försåld, lysande spagetti. Och Tralfamadorianer ser inte heller människor som tvåbenta varelser. De ser dem som stora tusenfotingar - "med spädbarns ben i ena änden och gamla människors ben i den andra", säger Billy Pilgrim.

Nästan alla science-fiction-berättelser som använder detta koncept aktivt, till exempel för att möjliggöra tidsresor , överförenklar detta koncept till en endimensionell tidslinje för att passa en linjär struktur, som inte passar modeller av verkligheten. Sådana tidsmaskiner framställs ofta som omedelbara, med dess innehåll som avgår en gång och anländer till en annan – men på samma bokstavliga geografiska punkt i rymden. Detta utförs ofta utan notering av en referensram, eller med det implicita antagandet att referensramen är lokal; som sådant skulle detta kräva antingen noggrann teleportering, eftersom en roterande planet, som är under acceleration, inte är en tröghetsram, eller för att tidsmaskinen ska förbli på samma plats, dess innehåll "fryst".

Författaren Oliver Franklin publicerade ett science fiction -verk 2008 med titeln World Lines där han berättade om en förenklad förklaring av hypotesen för lekmän.

I novellen Life-Line beskriver författaren Robert A. Heinlein en persons världslinje:

Han klev fram till en av reportrarna. "Anta att vi tar dig som ett exempel. Ditt namn är Rogers, är det inte? Mycket bra, Rogers, du är en rymd-tidshändelse som varar på fyra sätt. Du är inte riktigt sex fot lång, du är ungefär tjugo tum bred och kanske tio tum tjock. Med tiden sträcker sig bakom dig mer av denna rum-tidshändelse, och når kanske nitton-sexton, av vilka vi ser ett tvärsnitt här i rät vinkel mot tidsaxeln och lika tjockt som nuet Längst bort finns en bebis som luktar sur mjölk och dreglar sin frukost på haklappen. I andra änden ligger kanske en gammal man någonstans på 1980-talet. "Föreställ dig denna rum-tidshändelse som vi kallar

Rogers som en lång rosa mask, kontinuerlig genom åren, ena änden i sin mors mage och den andra vid graven..."

Heinleins Methuselah's Children använder termen, liksom James Blishs The Quincunx of Time (expanderat från "Beep").

En visuell roman med namnet Steins;Gate , producerad av 5pb. , berättar en historia baserad på förskjutningen av världslinjer. Steins;Gate är en del av serien " Science Adventure ". Världslinjer och andra fysiska koncept som Dirachavet används också genom hela serien.

Neal Stephensons roman Anathem involverar en lång diskussion om världslinjer under middagen mitt i en filosofisk debatt mellan platonsk realism och nominalism .

Absolute Choice skildrar olika världslinjer som en sub-plot och inställningsanordning.

En rymdarmada som försöker slutföra en (nästan) stängd tidsliknande väg som en strategisk manöver bildar bakgrunden och en huvudsaklig handling i "Singularity Sky" av Charles Stross .

Se även

• Specifika typer av världslinjer
  • Geodesik
  • Stängda tidsliknande kurvor
  • Orsaksstruktur , kurvor som representerar en mängd olika typer av världslinje
  • Isotrop linje
• Feynman diagram
• Tidsgeografi

• Minkowski, Hermann (1909), "Raum und Zeit" , Physikalische Zeitschrift , 10 : 75–88

• Olika engelska översättningar på Wikisource: Space and Time

• Ludwik Silberstein (1914) Theory of Relativity , s 130, Macmillan and Company .

externa länkar

• World lines artikel om h2g2 .

• fördjupad text om världslinjer och speciell relativitet