Stress (mekanik)

Stress
Stress
	Restspänningar inuti en gradskiva av plast avslöjas av det polariserade ljuset .
Vanliga symboler	σ
SI-enhet	pascal
Andra enheter	psi , bar
I SI-basenheter	Pa = kg ⋅ m −1 ⋅ s −2
Dimensionera

I kontinuummekanik är stress en fysisk storhet som beskriver storleken på krafter som orsakar deformation . Spänning definieras som kraft per ytenhet . När ett föremål dras isär av en kraft kommer det att orsaka förlängning som också kallas deformation, som sträckning av ett elastiskt band, det kallas dragspänning. Men när krafterna resulterar i kompression av ett föremål, kallas det tryckspänning. Det uppstår när krafter som spänning eller kompression verkar på en kropp. Ju större denna kraft och ju mindre tvärsnittsarea av den kropp som den verkar på, desto större påkänning. Därför mäts spänningen i newton per kvadratmeter (N/m ² ) eller pascal (Pa).

Stress uttrycker de inre krafter som närliggande partiklar av ett kontinuerligt material utövar på varandra, medan töjning är måttet på materialets deformation. Till exempel, när en solid vertikal stång stödjer en övervikt, trycker varje partikel i stången på partiklarna omedelbart under den. När en vätska är i en sluten behållare under tryck , trycks varje partikel emot av alla omgivande partiklar. Behållarväggarna och den tryckinducerande ytan (som en kolv) trycker mot dem i (Newtonsk) reaktion . Dessa makroskopiska krafter är faktiskt nettoresultatet av ett mycket stort antal intermolekylära krafter och kollisioner mellan partiklarna i dessa molekyler . Stress representeras ofta av en grekisk liten bokstav sigma ( σ ).

Påkänning inuti ett material kan uppstå av olika mekanismer, såsom stress som appliceras av yttre krafter på bulkmaterialet (som gravitation ) eller på dess yta (som kontaktkrafter , yttre tryck eller friktion ). Varje töjning (deformation) av ett fast material genererar en inre elastisk spänning , analog med reaktionskraften hos en fjäder , som tenderar att återställa materialet till dess ursprungliga icke-deformerade tillstånd. I vätskor och gaser genererar endast deformationer som ändrar volymen ihållande elastisk stress. Men om deformationen ändras gradvis med tiden, även i vätskor kommer det vanligtvis att finnas viss viskös spänning , som motverkar den förändringen. Elastiska och viskösa spänningar kombineras vanligtvis under namnet mekanisk spänning .

Mekanisk stress

Betydande spänningar kan förekomma även när deformationen är försumbar eller obefintlig (ett vanligt antagande vid modellering av vattenflödet). Stress kan existera i frånvaro av yttre krafter; sådan inbyggd spänning är viktig, till exempel i förspänd betong och härdat glas . Stress kan också utsättas för ett material utan applicering av nettokrafter , till exempel genom förändringar i temperatur eller kemisk sammansättning, eller av externa elektromagnetiska fält (som i piezoelektriska och magnetostriktiva material).

Relationen mellan mekanisk påkänning, deformation och förändringshastigheten för deformation kan vara ganska komplicerad, även om en linjär approximation kan vara tillräcklig i praktiken om kvantiteterna är tillräckligt små. Stress som överskrider vissa hållfasthetsgränser för materialet kommer att resultera i permanent deformation (såsom plastiskt flöde , brott , kavitation ) eller till och med ändra dess kristallstruktur och kemiska sammansättning .

Historia

Romerska eran bro i Schweiz . Stenvalven i bron utsätts för tryckspänningar .

Inkabron på Apurimacfloden . Repet i bron utsätts för dragpåkänningar .

Människor har känt till stress inuti material sedan urminnes tider. Fram till 1600-talet var denna förståelse till stor del intuitiv och empirisk, även om detta inte hindrade utvecklingen av relativt avancerad teknik som kompositbågen och glasblåsning .

Under flera årtusenden har särskilt arkitekter och byggare lärt sig hur man sätter ihop noggrant formade träbjälkar och stenblock för att motstå, överföra och fördela påfrestningar på det mest effektiva sättet, med geniala anordningar som kapitäler , valv , kupoler , takstolar och de flygande strävpelarna i gotiska katedraler .

Forntida och medeltida arkitekter utvecklade vissa geometriska metoder och enkla formler för att beräkna de rätta storlekarna på pelare och balkar, men den vetenskapliga förståelsen av stress blev möjlig först efter att de nödvändiga verktygen uppfanns på 1600- och 1700-talen: Galileo Galileis rigorösa experimentella metod , René Descartes koordinater och analytiska geometri , och Newtons rörelselagar och jämvikt och infinitesimalanalys . Med dessa verktyg kunde Augustin-Louis Cauchy ge den första rigorösa och generella matematiska modellen av en deformerad elastisk kropp genom att introducera begreppen stress och belastning. Cauchy observerade att kraften över en imaginär yta var en linjär funktion av dess normalvektor; och dessutom att det måste vara en symmetrisk funktion (med noll totalt rörelsemängd). Förståelsen av stress i vätskor började med Newton, som gav en differentialformel för friktionskrafter (skjuvspänning) i parallellt laminärt flöde .

Översikt

Definition

Spänning definieras som kraften över en "liten" gräns per ytenhet av den gränsen, för alla orienteringar av gränsen. Eftersom spänningen härleds från en fundamental fysisk storhet (kraft) och en rent geometrisk storhet (area), är spänningen också en fundamental storhet, som hastighet, vridmoment eller energi , som kan kvantifieras och analyseras utan explicit hänsyn till materialets natur eller dess fysiska orsaker.

Spänningen över ett ytelement (gul skiva) är den kraft som materialet på ena sidan (toppkulan) utövar på materialet på den andra sidan (bottenkulan), dividerat med ytans yta.

Efter kontinuummekanikens grundläggande premisser är stress ett makroskopiskt begrepp. De partiklar som beaktas i dess definition och analys bör nämligen vara precis tillräckligt små för att kunna behandlas som homogena i sammansättning och tillstånd, men ändå tillräckligt stora för att ignorera kvanteffekter och molekylernas detaljerade rörelser. Således är kraften mellan två partiklar faktiskt medelvärdet av ett mycket stort antal atomkrafter mellan deras molekyler; och fysiska storheter som massa, hastighet och krafter som verkar genom huvuddelen av tredimensionella kroppar, som gravitationen, antas vara jämnt fördelade över dem. Beroende på sammanhanget kan man också anta att partiklarna är tillräckligt stora för att möjliggöra ett medelvärde av andra mikroskopiska egenskaper, som kornen på en metallstav eller fibrerna i en träbit .

Kvantitativt uttrycks spänningen av Cauchy-dragvektorn T definierad som dragkraften F mellan intilliggande delar av materialet över en imaginär separeringsyta S , dividerat med arean av S . I en vätska i vila är kraften vinkelrät mot ytan och är det välkända trycket . I ett fast ämne , eller i ett flöde av trögflytande vätska , kanske kraften F inte är vinkelrät mot S ; därför måste spänningen över en yta betraktas som en vektorkvantitet, inte en skalär. Dessutom beror riktningen och magnituden i allmänhet på orienteringen av S. Således måste spänningstillståndet för materialet beskrivas av en tensor , kallad (Cauchy) spänningstensor ; som är en linjär funktion som relaterar normalvektorn n för en yta S till dragvektorn T över S . Med avseende på vilket valt koordinatsystem som helst , kan Cauchy-spänningstensorn representeras som en symmetrisk matris av 3×3 reella tal. Även inom en homogen kropp kan spänningstensorn variera från plats till plats och kan förändras över tiden; därför är spänningen i ett material i allmänhet ett tidsvarierande tensorfält .

Normal och skjuvspänning

I allmänhet kan spänningen T som en partikel P applicerar på en annan partikel Q över en yta S ha vilken riktning som helst i förhållande till S . Vektorn T kan betraktas som summan av två komponenter: normalspänningen ( parallell kompression eller spänning ) vinkelrät mot ytan, och skjuvspänningen som är med ytan.

ytans normalenhetsvektor n (som pekar från Q mot P ) antas fixerad kan normalkomponenten uttryckas med ett enda tal, punktprodukten T · n . Detta tal kommer att vara positivt om P "drar" på Q (dragspänning), och negativt om P "skjuter" mot Q (tryckspänning) Skjuvkomponenten är då vektorn T − ( T · n ) n .

Enheter

Spänningens dimension är trycket och därför mäts dess koordinater i samma enheter som trycket: nämligen pascal (Pa, det vill säga newton per kvadratmeter ) i det internationella systemet , eller pund per kvadrattum (psi) i det kejserliga systemet . Eftersom mekaniska spänningar lätt överstiger en miljon Pascal, är MPa, som står för megapascal, en vanlig spänningsenhet.

Orsaker och effekter

Glasvas med craquelé -effekt. Sprickorna är resultatet av korta men intensiva påfrestningar som skapas när den halvsmälta biten kort doppas i vatten.

Stress i en materiell kropp kan bero på flera fysiska orsaker, inklusive yttre påverkan och inre fysiska processer. Vissa av dessa ämnen (som gravitation, förändringar i temperatur och fas och elektromagnetiska fält) verkar på huvuddelen av materialet och varierar kontinuerligt med position och tid. Andra ämnen (som yttre belastningar och friktion, omgivande tryck och kontaktkrafter) kan skapa spänningar och krafter som är koncentrerade på vissa ytor, linjer eller punkter; och möjligen även på mycket korta tidsintervall (som i impulserna på grund av kollisioner). I aktivt material genererar självframdrivning av mikroskopiska partiklar makroskopiska spänningsprofiler. Generellt uttrycks spänningsfördelningen i en kropp som en styckvis kontinuerlig funktion av rum och tid.

Omvänt är stress vanligtvis korrelerad med olika effekter på materialet, möjligen inklusive förändringar i fysikaliska egenskaper som dubbelbrytning , polarisering och permeabilitet . Påförandet av stress av ett externt medel skapar vanligtvis en viss spänning (deformation) i materialet, även om det är för litet för att upptäckas. I ett fast material kommer en sådan töjning i sin tur att generera en inre elastisk spänning, analog med reaktionskraften hos en sträckt fjäder , som tenderar att återställa materialet till dess ursprungliga odeformerade tillstånd. Flytande material (vätskor, gaser och plasma ) kan per definition bara motsätta sig deformationer som skulle ändra deras volym. Men om deformationen förändras med tiden, även i vätskor kommer det vanligtvis att finnas viss viskös spänning, som motverkar den förändringen. Sådana spänningar kan vara antingen skjuvkrafter eller normala. Molekylärt ursprung för skjuvspänningar i vätskor anges i artikeln om viskositet . Samma sak för normala viskösa spänningar finns i Sharma (2019).

Relationen mellan stress och dess effekter och orsaker, inklusive deformation och förändringshastighet av deformation, kan vara ganska komplicerad (även om en linjär approximation kan vara tillräcklig i praktiken om kvantiteterna är tillräckligt små). Stress som överskrider vissa hållfasthetsgränser för materialet kommer att resultera i permanent deformation (såsom plastiskt flöde , brott , kavitation ) eller till och med ändra dess kristallstruktur och kemiska sammansättning .

Enkel stress

I vissa situationer kan spänningen i en kropp beskrivas på ett adekvat sätt med ett enda nummer eller med en enda vektor (ett tal och en riktning). Tre sådana enkla spänningssituationer , som ofta uppstår i teknisk design, är den enaxliga normalspänningen , den enkla skjuvspänningen och den isotropiska normalspänningen .

Enaxlig normal stress

Idealiserad spänning i en rak stång med enhetligt tvärsnitt.

En vanlig situation med ett enkelt spänningsmönster är när en rak stång, med enhetligt material och tvärsnitt, utsätts för spänning av motsatta krafter av storleken $F$ längs sin axel. Om systemet är i jämvikt och inte förändras med tiden, och vikten av stången kan försummas, måste överdelen genom varje tvärgående sektion av stången dra i den nedre delen med samma kraft, F med kontinuitet genom hela tvärsnittsarea , A . Därför kan spänningen σ genom hela stången, över vilken horisontell yta som helst, uttryckas helt enkelt med det enda talet σ, beräknat helt enkelt med storleken på dessa krafter, F , och tvärsnittsarean, A .

\sigma ={\frac {F}{A}}

Å andra sidan, om man föreställer sig att stången skärs längs sin längd, parallellt med axeln, kommer det inte att finnas någon kraft (därav ingen spänning) mellan de två halvorna över snittet. Denna typ av spänning kan kallas (enkel) normal spänning eller enaxlig spänning; specifikt (enaxlig, enkel, etc.) dragspänning. Om belastningen är kompression på stången, snarare än att sträcka den, är analysen densamma förutom att kraften F och spänningen

\sigma

byter tecken, och spänningen kallas tryckspänning.

Förhållandet

\sigma =F/A

kan endast vara en medelspänning. Spänningen kan vara ojämnt fördelad över tvärsnittet ( m – m ), särskilt nära fästpunkterna ( n – n ).

Denna analys antar att spänningen är jämnt fördelad över hela tvärsnittet. I praktiken, beroende på hur stången är fäst i ändarna och hur den tillverkades, kanske detta antagande inte är giltigt. I så fall kommer värdet $\sigma$ = F / A endast att vara medelspänningen, kallad teknisk spänning eller nominell spänning . Men om stångens längd L är många gånger dess diameter D , och den inte har några grova defekter eller inbyggd spänning, kan spänningen antas vara jämnt fördelad över varje tvärsnitt som är mer än några gånger D från båda ändarna. (Denna observation är känd som Saint-Venants princip ).

Normal stress förekommer i många andra situationer förutom axiell spänning och kompression. Om en elastisk stång med likformigt och symmetriskt tvärsnitt böjs i ett av dess symmetriplan kommer den resulterande böjspänningen fortfarande att vara normal (vinkelrätt mot tvärsnittet), men kommer att variera över tvärsnittet: den yttre delen kommer att vara under dragspänning, medan den inre delen kommer att komprimeras. En annan variant av normal spänning är ringspänningen som uppstår på väggarna i ett cylindriskt rör eller kärl fyllt med trycksatt vätska.

Enkel skjuvspänning

Skjuvspänning i en horisontell stång belastad av två förskjutna block.

En annan enkel typ av påkänning uppstår när ett jämnt tjockt lager av elastiskt material som lim eller gummi är fast fäst vid två styva kroppar som dras i motsatta riktningar av krafter parallella med lagret; eller en del av en mjuk metallstång som skärs av käkarna på ett saxliknande verktyg . Låt F vara storleken på dessa krafter och M vara mittplanet för det lagret. Precis som i det normala spänningsfallet måste delen av lagret på ena sidan av M dra den andra delen med samma kraft F . Om man antar att krafternas riktning är känd, kan spänningen över M uttryckas helt enkelt med det enda talet ${\displaystyle \tau } ,$ beräknat helt enkelt med storleken på dessa krafter, F och tvärsnittsarean, A .

\tau ={\frac {F}{A}}

Men till skillnad från normal spänning är denna enkla skjuvspänning riktad parallellt med det betraktade tvärsnittet snarare än vinkelrätt mot det. För vilket plan S som helst som är vinkelrätt mot skiktet kommer den inre nettokraften över S , och därmed spänningen, att vara noll.

Liksom i fallet med en axiellt belastad stång kan i praktiken skjuvspänningen inte vara jämnt fördelad över skiktet; så, som tidigare, kommer förhållandet F / A endast att vara en genomsnittlig ("nominell", "teknisk") spänning. Det genomsnittet är dock ofta tillräckligt för praktiska ändamål. Skjuvspänning observeras även när en cylindrisk stång, såsom en axel , utsätts för motsatta vridmoment vid sina ändar. I så fall är skjuvspänningen på varje tvärsnitt parallell med tvärsnittet, men orienterad tangentiellt relativt axeln och ökar med avståndet från axeln. Betydande skjuvspänning uppstår i mellanplattan ("banan") av I-balkar under böjbelastningar, på grund av att banan begränsar ändplattorna ("flänsar").

Isotropisk stress

Isotropisk dragspänning. Överst till vänster: Varje yta av en kub av homogent material dras av en kraft med magnituden F , som appliceras jämnt över hela ytan vars area är A . Kraften över varje sektion S av kuben måste balansera krafterna som appliceras under sektionen. I de tre sektionerna som visas är krafterna F (överst till höger), F

{\sqrt {2}}

(nederst till vänster) och F

{\sqrt {3}}/2

(nedre till höger); och arean av S är A , A

{\sqrt {2}}

respektive A

2

. Så stressen över S är F / A i alla tre fallen.

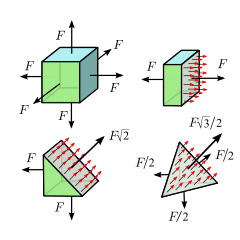
En annan enkel typ av spänning uppstår när materialkroppen är under lika kompression eller spänning i alla riktningar. Detta är fallet, till exempel, i en del av vätska eller gas i vila, vare sig den är innesluten i någon behållare eller som en del av en större mängd vätska; eller inuti en kub av elastiskt material som pressas eller dras på alla sex ytorna med lika vinkelräta krafter - förutsatt att materialet i båda fallen är homogent, utan inbyggd spänning, och att tyngdkraftens inverkan och andra yttre krafter kan försummas.

I dessa situationer visar sig spänningen över en imaginär inre yta vara lika stor och alltid riktad vinkelrätt mot ytan oberoende av ytans orientering. Denna typ av stress kan kallas isotropisk normal eller bara isotropisk ; om det är kompressivt kallas det hydrostatiskt tryck eller bara tryck . Gaser kan per definition inte motstå dragpåkänningar, men vissa vätskor kan motstå mycket stora mängder isotrop dragpåkänning under vissa omständigheter. se Z-rör .

Cylinderspänningar

Delar med rotationssymmetri , såsom hjul, axlar, rör och pelare, är mycket vanliga inom teknik. Ofta har de spänningsmönster som uppstår i sådana delar rotations- eller till och med cylindrisk symmetri . Analysen av sådana cylinderspänningar kan dra fördel av symmetrin för att reducera dimensionen av domänen och/eller spänningstensorn.

Allmän stress

Ofta upplever mekaniska kroppar mer än en typ av stress samtidigt; detta kallas kombinerad stress . Vid normal- och skjuvspänning är storleken på spänningen maximal för ytor som är vinkelräta mot en viss riktning $\displaystyle d} ,$ och noll över alla ytor som är parallella med $d$ . När skjuvspänningen är noll endast över ytor som är vinkelräta mot en viss riktning, kallas spänningen biaxiell och kan ses som summan av två normala eller skjuvspänningar. I det mest allmänna fallet, kallat triaxiell spänning , är spänningen icke-noll över varje ytelement.

Cauchy stresstensor

Komponenter av stress i tre dimensioner

Illustration av typiska spänningar (pilar) över olika ytelement på gränsen för en partikel (sfär), i ett homogent material under enhetlig (men inte isotrop) triaxiell spänning. Normalspänningarna på huvudaxlarna är +5, +2 och −3 enheter.

Kombinerade spänningar kan inte beskrivas av en enda vektor. Även om materialet belastas på samma sätt genom hela kroppens volym, kommer spänningen över vilken imaginär yta som helst att bero på orienteringen av den ytan, på ett icke-trivialt sätt.

Emellertid observerade Cauchy att spänningsvektorn $T$ över en yta alltid kommer att vara en linjär funktion av ytans normalvektor $n$ , den enhetslängdsvektor som är vinkelrät mot den. Det vill säga $T={\boldsymbol {\sigma }}(n)$ , där funktionen ${\boldsymbol {\sigma }}$ uppfyller

{\boldsymbol {\sigma }}(\alpha u+\beta v)=\alpha {\boldsymbol {\sigma }} (u)+\beta {\boldsymbol {\sigma }}(v)

för alla vektorer $u,v$ och eventuella reella tal $\alpha ,\beta$ . Funktionen ${\boldsymbol {\sigma }}$ , nu kallad (Cauchy) spänningstensor , beskriver fullständigt spänningstillståndet hos en likformigt belastad kropp. (Idag kallas varje linjär koppling mellan två fysiska vektorkvantiteter en tensor , vilket återspeglar Cauchys ursprungliga användning för att beskriva "spänningarna" (spänningarna) i ett material.) I tensorkalkylen $}$ ${\boldsymbol {\sigma$ } klassificeras som andra ordningens tensor av typen (0,2) .

Liksom vilken linjär karta som helst mellan vektorer kan spänningstensorn representeras i vilket som helst valt kartesiskt koordinatsystem av en 3×3-matris av reella tal. Beroende på om koordinaterna är numrerade $x_{1},x_{2},x_{3}$ eller namngivna $x,y,z$ , matrisen kan skrivas som

{\begin{bmatrix}\sigma _{11}&\sigma _{12}&\sigma _{1} \\sigma _{21}&\sigma _{22}&\sigma _{23}\\\sigma _{31}&\sigma _{32}&\sigma _{33}\end{bmatrix}}

eller

{\begin{bmatrix}\sigma _{xx}&\sigma _{xy }&\sigma _{xz}\\\sigma _{yx}&\sigma _{yy}&\sigma _{yz}\\\sigma _{zx}&\sigma _{zy}&\sigma _{ zz}\\\end{bmatrix}}

Spänningsvektorn

T={\boldsymbol {\sigma }}(n)

över en yta med normalvektor

n

(som är kovariant - "rad; horisontell" - vektor ) med koordinater

n_{1},n_{2},n_{3}

är då en matrisprodukt

T=n\cdot {\boldsymbol {\sigma }}

(där T i övre index är transposition , och som ett resultat får vi kovariant (rad) vektor ) (titta på Cauchy stress tensor ), det vill säga

{\displaystyle {\begin{bmatrix}T_{1}&T_{2}&T_{

Den linjära relationen mellan $T$ och $n$ följer av de grundläggande lagarna för bevarande av linjärt momentum och statisk jämvikt av krafter, och är därför matematiskt exakt, för alla material och alla spänningssituationer. Komponenterna i Cauchy-spänningstensorn vid varje punkt i ett material uppfyller jämviktsekvationerna ( Cauchys rörelseekvationer för nollacceleration). Dessutom innebär principen för bevarande av rörelsemängd att spänningstensorn är symmetrisk , det vill säga ${\displaystyle \sigma _{12}=\sigma _{21}} ,$ σ $\displaystyle \sigma _{13}=\sigma _{31}}$ och $\sigma _{23}=\sigma _{32}$ . Därför kan mediets spänningstillstånd vid vilken punkt och ögonblick som helst specificeras med endast sex oberoende parametrar, snarare än nio. Dessa kan vara skrivna

{\begin{bmatrix}\sigma _{x}&\tau _{xy}&\ tau _{xz}\\\tau _{xy}&\sigma _{y}&\tau _{yz}\\\tau _{xz}&\tau _{yz}&\sigma _{z}\ slut{bmatrix}}

där elementen $\sigma _{x},\sigma _{y},\sigma _{z}$ kallas de ortogonala normalspänningarna (relativt det valda koordinatsystemet), och $\tau _{xy},\tau _{xz},\tau _{yz}$ de ortogonala skjuvspänningarna . ^{[ citat behövs ]}

Ändring av koordinater

Cauchy-spänningstensorn lyder tensortransformationslagen under en förändring i koordinatsystemet. En grafisk representation av denna transformationslag är Mohrs cirkel av spänningsfördelning.

Som en symmetrisk 3×3 reell matris har spänningstensorn $\boldsymbol {\sigma }}}$ { tre ömsesidigt ortogonala längdenhetsvektorer $e_{1},e_ {2},e_{3}$ och tre reella egenvärden ${\displaystyle \lambda _{1},\lambda _{2},\lambda _{3}} ,$ så att ${\boldsymbol {\sigma }}e_{i}=\lambda _{i}e_{i}$ . Därför, i ett koordinatsystem med axlarna $e_{1},e_{2},e_{3}$ , är spänningstensorn en diagonal matris och har endast de tre normala komponenterna $\lambda _{1},\lambda _{2},\lambda _{3$ } huvudspänningen . Om de tre egenvärdena är lika, är spänningen en isotropisk kompression eller spänning, alltid vinkelrät mot vilken yta som helst, det finns ingen skjuvspänning och tensorn är en diagonal matris i vilken koordinatram som helst.

Stress som ett tensorfält

I allmänhet är stress inte jämnt fördelad över en materiell kropp och kan variera med tiden. Därför måste spänningstensorn definieras för varje punkt och varje ögonblick, genom att betrakta en oändligt liten partikel av mediet som omger den punkten, och ta medelspänningarna i den partikeln som spänningarna vid punkten.

Stress i tunna plattor

En tankvagn gjord av böjda och svetsade stålplåtar.

Konstgjorda föremål tillverkas ofta av lagerplåtar av olika material genom operationer som inte ändrar deras väsentligen tvådimensionella karaktär, som skärning, borrning, försiktig bockning och svetsning längs kanterna. Beskrivningen av spänningar i sådana kroppar kan förenklas genom att modellera dessa delar som tvådimensionella ytor snarare än tredimensionella kroppar.

I den uppfattningen omdefinierar man en "partikel" som en oändlig del av plattans yta, så att gränsen mellan intilliggande partiklar blir ett oändligt litet linjeelement; båda är implicit förlängda i den tredje dimensionen, vinkelräta mot (rakt genom) plattan. "Stress" omdefinieras sedan som ett mått på de inre krafterna mellan två intilliggande "partiklar" över deras gemensamma linjeelement, dividerat med längden på den linjen. Vissa komponenter i spänningstensorn kan ignoreras, men eftersom partiklar inte är oändligt små i den tredje dimensionen kan man inte längre bortse från det vridmoment som en partikel applicerar på sina grannar. Det vridmomentet är modellerat som en böjspänning som tenderar att förändra plattans krökning . Dessa förenklingar kanske inte håller vid svetsar, vid skarpa böjar och veck (där krökningsradien är jämförbar med plåtens tjocklek).

Spänning i tunna balkar

För stressmodellering kan en fiskespö anses vara endimensionell.

Analysen av spänningar kan avsevärt förenklas även för tunna stänger, balkar eller trådar med enhetlig (eller jämnt varierande) sammansättning och tvärsnitt som utsätts för måttlig böjning och vridning. För dessa kroppar kan man överväga endast tvärsnitt som är vinkelräta mot stångens axel, och omdefiniera en "partikel" som en tråd med oändlig längd mellan två sådana tvärsnitt. Den ordinarie spänningen reduceras sedan till en skalär (spänning eller kompression av stången), men man måste också ta hänsyn till en böjspänning (som försöker ändra stångens krökning, i någon riktning vinkelrät mot axeln) och en vridspänning ( som försöker vrida eller avvrida den kring sin axel).

Andra beskrivningar av stress

Härdat glas av bilens bakruta. Variationer i glasspänningen ses tydligt när de fotograferas genom ett polariserande filter (nedre bilden).

Cauchy-spänningstensorn används för spänningsanalys av materialkroppar som upplever små deformationer där skillnaderna i spänningsfördelning i de flesta fall kan försummas. För stora deformationer, även kallade finita deformationer , krävs andra spänningsmått, såsom den första och andra Piola–Kirchhoff-spänningstensorn , Biot-spänningstensorn och Kirchhoff-spänningstensorn . Fasta ämnen, vätskor och gaser har spänningsfält . Statiska vätskor stöder normal spänning men kommer att flyta under skjuvpåkänning . Rörliga viskösa vätskor kan stödja skjuvspänning (dynamiskt tryck). Fasta ämnen kan stödja både skjuvning och normal spänning, med duktila material som misslyckas under skjuvning och spröda material sviker under normal belastning. Alla material har temperaturberoende variationer i spänningsrelaterade egenskaper, och icke-newtonska material har hastighetsberoende variationer.

Stressanalys

Spänningsanalys är en gren av tillämpad fysik som täcker bestämningen av den inre fördelningen av inre krafter i fasta föremål. Det är ett viktigt verktyg inom teknik för studier och design av strukturer som tunnlar, dammar, mekaniska delar och strukturella ramar, under föreskrivna eller förväntade belastningar. Det är också viktigt inom många andra discipliner; till exempel, inom geologi, för att studera fenomen som plattektonik , vulkanism och laviner ; och i biologi, att förstå anatomin hos levande varelser.

Mål och antaganden

Spänningsanalys handlar i allmänhet om objekt och strukturer som kan antas vara i makroskopisk statisk jämvikt . Enligt Newtons rörelselagar måste alla yttre krafter som appliceras på ett sådant system balanseras av interna reaktionskrafter, som nästan alltid är ytkontaktkrafter mellan intilliggande partiklar - det vill säga som spänning. Eftersom varje partikel måste vara i jämvikt, kommer denna reaktionsspänning i allmänhet att sprida sig från partikel till partikel, vilket skapar en stressfördelning i hela kroppen. Det typiska problemet vid spänningsanalys är att fastställa dessa inre spänningar, givet de yttre krafter som verkar på systemet. De senare kan vara kroppskrafter (såsom gravitation eller magnetisk attraktion), som verkar genom hela volymen av ett material; eller koncentrerade belastningar (såsom friktion mellan en axel och ett lager , eller vikten av ett tåghjul på en räl), som är tänkt att verka över ett tvådimensionellt område, eller längs en linje, eller vid en enda punkt.

Vid spänningsanalys bortser man normalt från de fysiska orsakerna till krafterna eller materialens exakta natur. Istället antar man att spänningarna är relaterade till deformation (och, i icke-statiska problem, till deformationshastigheten) av materialet med kända konstitutiva ekvationer .

Metoder

Spänningsanalys kan utföras experimentellt, genom att applicera belastningar på den faktiska artefakten eller på skalmodell, och mäta de resulterande spänningarna, med någon av flera tillgängliga metoder. Detta tillvägagångssätt används ofta för säkerhetscertifiering och övervakning. Men de flesta stressanalyser görs med matematiska metoder, speciellt under design. Det grundläggande spänningsanalysproblemet kan formuleras av Eulers rörelseekvationer för kontinuerliga kroppar (som är konsekvenser av Newtons lagar för bevarande av linjärt momentum och vinkelmomentum ) och Euler-Cauchys spänningsprincip, tillsammans med lämpliga konstitutiva ekvationer. Således erhåller man ett system av partiella differentialekvationer som involverar spänningstensorfältet och töjningstensorfältet , som okända funktioner som ska bestämmas. De yttre kroppskrafterna framträder som den oberoende ("högra sidan") termen i differentialekvationerna, medan de koncentrerade krafterna uppträder som randvillkor. Det grundläggande stressanalysproblemet är därför ett gränsvärdeproblem .

Spänningsanalys för elastiska strukturer bygger på teorin om elasticitet och infinitesimal töjningsteori . När de applicerade belastningarna orsakar permanent deformation måste man använda mer komplicerade konstitutiva ekvationer, som kan redogöra för de inblandade fysikaliska processerna ( plastiskt flöde , brott , fasförändring , etc.). Emellertid är konstruerade strukturer vanligtvis utformade så att de maximala förväntade spänningarna ligger väl inom intervallet för linjär elasticitet (generaliseringen av Hookes lag för kontinuerliga media); det vill säga deformationerna som orsakas av inre spänningar är linjärt relaterade till dem. I detta fall är differentialekvationerna som definierar spänningstensorn linjära, och problemet blir mycket lättare. För det första kommer spänningen vid vilken punkt som helst att vara en linjär funktion av lasterna också. För tillräckligt små spänningar kan även icke-linjära system vanligtvis antas vara linjära.

Förenklad modell av en fackverk för spänningsanalys, med antagande av endimensionella element under enhetlig axiell spänning eller kompression.

Spänningsanalys förenklas när de fysiska dimensionerna och fördelningen av laster gör att konstruktionen kan behandlas som en- eller tvådimensionell. Vid analys av fackverk, till exempel, kan spänningsfältet antas vara enhetligt och enaxligt över varje element. Därefter reduceras differentialekvationerna till en ändlig uppsättning ekvationer (vanligtvis linjära) med ändligt många okända. I andra sammanhang kan man kanske reducera det tredimensionella problemet till ett tvådimensionellt, och/eller ersätta de allmänna spännings- och töjnings-tensorerna med enklare modeller som uniaxial spänning/kompression, enkel skjuvning, etc.

Ändå, för två- eller tredimensionella fall måste man lösa ett partiellt differentialekvationsproblem. Analytiska eller slutna lösningar av differentialekvationerna kan erhållas när geometrin, konstitutiva relationer och randvillkor är enkla nog. Annars måste man generellt ta till numeriska approximationer såsom finita elementmetoden , finita differensmetoden och boundary elementmetoden .

Alternativa mått på stress

Andra användbara spänningsmått inkluderar den första och andra Piola–Kirchhoff-spänningstensoren , Biot-spänningstensorn och Kirchhoff-spänningstensorn .

Piola–Kirchhoff stresstensor

I fallet med ändliga deformationer uttrycker Piola –Kirchhoff-spänningstensorerna spänningen i förhållande till referenskonfigurationen. Detta i motsats till Cauchy-spänningstensorn som uttrycker spänningen relativt den nuvarande konfigurationen. För infinitesimala deformationer och rotationer är Cauchy- och Piola–Kirchhoff-tensorerna identiska. Medan Cauchy-spänningstensorn ${\boldsymbol {\sigma }}$ relaterar spänningar i den aktuella konfigurationen, beskrivs deformationsgradienten och töjningstensorerna genom att relatera rörelsen till referenskonfigurationen; sålunda är inte alla tensorer som beskriver materialets tillstånd i antingen referens- eller nuvarande konfiguration. Att beskriva spänningen, töjningen och deformationen antingen i referens- eller nuvarande konfiguration skulle göra det lättare att definiera konstitutiva modeller (exempelvis är Cauchy Stress-tensorn en variant av en ren rotation, medan deformationstöjningens tensor är invariant, vilket skapar problem med att definiera en konstitutiv modell som relaterar en varierande tensor, i termer av en invariant under ren rotation, eftersom konstitutiva modeller per definition måste vara invarianta till rena rotationer). Den första Piola–Kirchhoff-spänningstensorn, ${\boldsymbol {P}}$ är en möjlig lösning på detta problem. Den definierar en familj av tensorer, som beskriver kroppens konfiguration i antingen nuvarande eller referensläge. Den 1:a Piola–Kirchhoff-spänningstensorn, ${\boldsymbol {P}}$ relaterar krafter i den nuvarande ("spatiala") konfigurationen med områden i referenskonfigurationen ("material").

{\boldsymbol {P}}=J~{\boldsymbol {\sigma }}~{\boldsymbol {F}}^{-T}~

där ${\boldsymbol {F}}$ är deformationsgradienten och $J=\det {\boldsymbol {F}}$ är den jakobianska determinanten .

När det gäller komponenter med avseende på en ortonormal grund ges den första Piola–Kirchhoff-spänningen av

P_{iL}=J~\sigma _{ik}~F_{Lk}^{-1} =J~\sigma _{ik}~{\cfrac {\partial X_{L}}{\partial x_{k}}}~\,\!

Eftersom den relaterar till olika koordinatsystem är den första Piola–Kirchhoff-spänningen en tvåpunktstensor . I allmänhet är det inte symmetriskt. Den första Piola–Kirchhoff-spänningen är 3D-generaliseringen av 1D-konceptet för ingenjörsstress .

Om materialet roterar utan att spänningstillståndet ändras (styv rotation), kommer komponenterna i 1:a Piola–Kirchhoff spänningstensor att variera med materialets orientering.

Den första Piola–Kirchhoff-spänningen är energikonjugat till deformationsgradienten.

2:a Piola–Kirchhoff spänningstensor

Medan den första Piola–Kirchhoff-spänningen relaterar krafter i den aktuella konfigurationen till områden i referenskonfigurationen, relaterar den andra Piola–Kirchhoff-spänningstensorn ${\boldsymbol {S}}$ krafter i referenskonfigurationen till områden i referensen konfiguration. Kraften i referenskonfigurationen erhålls via en mappning som bevarar det relativa förhållandet mellan kraftriktningen och areanormalen i referenskonfigurationen.

{\boldsymbol {S}}=J~{\boldsymbol {F}}^{-1}\cdot {\boldsymbol {\sigma }}\cdot {\boldsymbol {F}}^{-T}~ .

I indexnotation med avseende på en ortonormal basis,

S_{IL}=J~F_{Ik}^ {-1}~F_{Lm}^{-1}~\sigma _{km}=J~{\cfrac {\partial X_{I}}{\partial x_{k}}}~{\cfrac {\ partiell X_{L}}{\partial x_{m}}}~\sigma _{km}\!\,\!

Denna tensor, en enpunktstensor, är symmetrisk. Om materialet roterar utan en förändring av spänningstillståndet (styv rotation), förblir komponenterna i den andra Piola–Kirchhoff spänningstensorn konstanta, oavsett materialorientering.

Den andra Piola-Kirchhoff-spänningstensorn är energikonjugat till Green-Lagrange finita töjningstensor .

Se även

Vidare läsning

Chakrabarty, J. (2006). Teori om plasticitet (3 uppl.). Butterworth-Heinemann. s. 17–32. ISBN 0-7506-6638-2 .
Öl, Ferdinand Pierre; Elwood Russell Johnston; John T. DeWolf (1992). Mekanik av material . McGraw-Hill Professional. ISBN 0-07-112939-1 .
Brady, BHG; ET Brown (1993). Rock Mechanics For Underground Mining (Tredje upplagan). Kluwer Academic Publisher. s. 17–29. ISBN 0-412-47550-2 .
Chen, Wai-Fah; Baladi, GY (1985). Jordplasticitet, teori och genomförande . ISBN 0-444-42455-5 .
Chou, Pei Chi; Pagano, NJ (1992). Elasticitet: tensor, dyadiska och tekniska tillvägagångssätt . Dover böcker om teknik. Dover Publikationer. s. 1–33. ISBN 0-486-66958-0 .
Davis, RO; Selvadurai. APS (1996). Elasticitet och geomekanik . Cambridge University Press. s. 16–26. ISBN 0-521-49827-9 .
Dieter, GE (3 uppl.). (1989). Mekanisk metallurgi . New York: McGraw-Hill. ISBN 0-07-100406-8 .
Holtz, Robert D.; Kovacs, William D. (1981). En introduktion till geoteknik . Prentice-Halls serier för civilingenjör och ingenjörsmekanik. Prentice-Hall. ISBN 0-13-484394-0 .
Jones, Robert Millard (2008). Deformationsteori om plasticitet . Bull Ridge Corporation. s. 95–112. ISBN 978-0-9787223-1-9 .
Jumikis, Alfreds R. (1969). Teoretisk markmekanik: med praktiska tillämpningar till markmekanik och grundläggningsteknik . Van Nostrand Reinhold Co. ISBN 0-442-04199-3 .
Landau, LD och EMLifshitz. (1959). Teori om elasticitet .
Love, AEH (4 uppl.). (1944). Avhandling om den matematiska teorin om elasticitet . New York: Dover Publications. ISBN 0-486-60174-9 .
Marsden, JE; Hughes, TJR (1994). Matematiska grunder för elasticitet . Dover Publikationer. s. 132 –142. ISBN 0-486-67865-2 .
Parry, Richard Hawley Gray (2004). Mohrcirklar, spänningsvägar och geoteknik (2 uppl.). Taylor och Francis. s. 1–30. ISBN 0-415-27297-1 .
Rees, David (2006). Basic Engineering Plasticity – En introduktion med teknik- och tillverkningsapplikationer . Butterworth-Heinemann. s. 1–32. ISBN 0-7506-8025-3 .
Timosjenko, Stephen P. ; James Norman Goodier (1970). Theory of Elasticity (tredje upplagan). McGraw-Hill International Editions. ISBN 0-07-085805-5 .
Timosjenko, Stephen P. (1983). Materialets styrkahistoria: med en kort redogörelse för elasticitetsteorin och strukturlärans historia . Dover böcker om fysik. Dover Publikationer. ISBN 0-486-61187-6 .