Friktionskontaktmekanik

Kontaktmekanik är studiet av deformationen av fasta ämnen som berör varandra på en eller flera punkter. Detta kan delas in i tryck- och vidhäftningskrafter i riktningen vinkelrät mot gränsytan och friktionskrafter i tangentiell riktning. Friktionskontaktmekanik är studiet av deformation av kroppar i närvaro av friktionseffekter, medan friktionsfri kontaktmekanik antar frånvaron av sådana effekter.

Friktionskontaktmekanik handlar om ett stort antal olika skalor.

• På den makroskopiska skalan används den för undersökning av rörelsen hos kontaktande kroppar (se Kontaktdynamik ) . Till exempel beror studsningen av en gummikula på en yta på friktionsinteraktionen vid kontaktgränsytan. Här är den totala kraften kontra intryckning och sidoförskjutning av största vikt.
• På den mellanliggande skalan är man intresserad av de lokala spänningarna , töjningarna och deformationerna hos kontaktkropparna i och nära kontaktområdet. Till exempel för att härleda eller validera kontaktmodeller i makroskopisk skala, eller för att undersöka slitage och skador på kontaktkropparnas ytor. Användningsområden i denna skala är interaktion mellan däck och beläggning, interaktion mellan järnväg och hjul, rullager, etc.
• Slutligen, på mikroskopisk och nano-skala, används kontaktmekanik för att öka vår förståelse av tribologiska system (t.ex. undersöka friktionens ursprung) och för konstruktion av avancerade enheter som atomkraftsmikroskop och MEMS -enheter.

Den här sidan handlar huvudsakligen om den andra skalan: att få grundläggande insikt i spänningar och deformationer i och nära kontaktlappen, utan att ägna alltför mycket uppmärksamhet åt de detaljerade mekanismerna genom vilka de uppstår.

Historia

Flera kända vetenskapsmän, ingenjörer och matematiker bidrog till vår förståelse av friktion. De inkluderar Leonardo da Vinci , Guillaume Amontons , John Theophilus Desaguliers , Leonhard Euler och Charles-Augustin de Coulomb . Senare kompletterade Nikolai Pavlovich Petrov , Osborne Reynolds och Richard Stribeck denna förståelse med teorier om smörjning .

Deformation av fasta material undersöktes på 1600- och 1700-talen av Robert Hooke , Joseph Louis Lagrange och på 1800- och 1900-talen av d'Alembert och Timosjenko . När det gäller kontaktmekanik sticker det klassiska bidraget av Heinrich Hertz ut. Vidare är de grundläggande lösningarna av Boussinesq och Cerruti av primär betydelse för undersökningen av friktionskontaktproblem i den ( linjärt) elastiska regimen.

I järnvägsapplikationer vill man veta sambandet mellan krypning (hastighetsskillnad) $\xi$ och friktionskraften $F_{w}$ .

Klassiska resultat för ett äkta friktionskontaktproblem rör artiklarna av FW Carter (1926) och H. Fromm (1927). De presenterade oberoende av varandra förhållandet mellan kryp och krypkraft för en cylinder på ett plan eller för två cylindrar i stadig rullande kontakt med hjälp av Coulombs torrfriktionslag (se nedan). Dessa tillämpas på dragkraft för järnvägslok och för att förstå jaktsvängningen hos järnvägsfordon. När det gäller glidning beror de klassiska lösningarna på C. Cattaneo (1938) och RD Mindlin (1949), som övervägde den tangentiella förskjutningen av en sfär på ett plan (se nedan).

På 1950-talet växte intresset för järnvägshjulens rullande kontakt. 1958 Kenneth L. Johnson ett ungefärligt tillvägagångssätt för 3D-friktionsproblemet med Hertzian geometri, med antingen lateral eller spinnkrypning. Bland annat fann han att spinnkrypning, som är symmetrisk kring mitten av kontaktfältet, leder till en nettokraft i sidled under rullande förhållanden. Detta beror på skillnaderna mellan fram och akter i fördelningen av drag i kontaktlappen.

1967 publicerade Joost Jacques Kalker sin milstolpe doktorsavhandling om linjär teori för rullande kontakt. Denna teori är exakt för situationen med en oändlig friktionskoefficient, i vilket fall glidarean försvinner, och är approximativ för icke-försvinnande krypningar. Den utgår från Coulombs friktionslag, som mer eller mindre kräver (noggrannt) rena ytor. Denna teori är för massiva kroppar som t.ex. kontakt mellan järnväg och räls. När det gäller interaktion mellan väg och däck gäller ett viktigt bidrag den så kallade magiska däckformeln av Hans Pacejka .

På 1970-talet utarbetades många numeriska modeller. Särskilt variationsrika tillvägagångssätt , som de som förlitar sig på Duvaut och Lions teorier om existens och unikhet. Med tiden växte dessa till finita elementmetoder för kontaktproblem med allmänna materialmodeller och geometrier, och till halvrumsbaserade tillvägagångssätt för så kallade slätkantade kontaktproblem för linjärt elastiska material. Modeller av den första kategorin presenterades av Laursen och av Wriggers. Ett exempel på den senare kategorin är Kalkers KONTAKTmodell.

En nackdel med de välgrundade variationssätten är deras långa beräkningstider. Därför utarbetades många olika ungefärliga tillvägagångssätt också. Flera välkända ungefärliga teorier för det rullande kontaktproblemet är Kalkers FASTSIM-metod, Shen-Hedrick-Elkins-formeln och Polachs tillvägagångssätt.

Mer information om historien om hjul/rälskontaktproblemet finns i Knothes tidning. Ytterligare Johnson samlade i sin bok en enorm mängd information om kontaktmekanik och relaterade ämnen. När det gäller rullande kontaktmekanik presenteras även en översikt över olika teorier av Kalker. Slutligen är förfarandet för en CISM-kurs av intresse, som ger en introduktion till mer avancerade aspekter av rullande kontaktteori.

Problemformulering

Centralt i analysen av friktionskontaktproblem är förståelsen att påfrestningarna vid ytan av varje kropp är rumsligt varierande. Följaktligen varierar töjningarna och deformationerna av kropparna med positionen. Och rörelsen hos partiklarna hos de kontaktande kropparna kan vara olika på olika ställen: i en del av kontaktlappen kan partiklar från de motstående kropparna vidhäfta (klibba) till varandra, medan i andra delar av kontaktlappen relativ rörelse inträffar. Denna lokala relativa glidning kallas mikroslip .

Denna uppdelning av kontaktytan i stick- (vidhäftnings-) och glidområden visar sig bl.a. i slitage . Observera att slitage endast uppstår där kraften försvinner, vilket kräver påkänning och lokal relativ förskjutning (glidning) mellan de två ytorna.

Storleken och formen på själva kontaktlappen och dess vidhäftnings- och glidområden är i allmänhet okända i förväg. Om dessa var kända skulle de elastiska fälten i de två kropparna kunna lösas oberoende av varandra och problemet skulle inte längre vara ett kontaktproblem.

Tre olika komponenter kan urskiljas i ett kontaktproblem.

1. Först och främst är det deformationen av de separata kropparna som reaktion på belastningar som appliceras på deras ytor. Detta är ämnet för allmän kontinuummekanik . Det beror till stor del på kropparnas geometri och på deras ( konstitutiva ) materialbeteende (t.ex. elastisk vs plastisk respons, homogen vs skiktad struktur etc.).
2. För det andra finns det den övergripande rörelsen av kropparna i förhållande till varandra. Till exempel kan kropparna vara i vila (statik) eller närma sig varandra snabbt ( påverkan ), och kan flyttas (glida) eller roteras ( rullande ) över varandra. Dessa övergripande rörelser studeras generellt inom klassisk mekanik , se till exempel multikroppsdynamik .
3. Slutligen finns det processerna vid kontaktgränssnittet : kompression och vidhäftning i riktningen vinkelrät mot gränsytan, och friktion och mikroglidning i tangentiella riktningar .

Den sista aspekten är kontaktmekanikens primära oro. Det beskrivs i termer av så kallade kontaktvillkor . För riktningen vinkelrät mot gränssnittet, det normala kontaktproblemet, är adhesionseffekterna vanligtvis små (vid större rumsliga skalor) och följande förhållanden används vanligtvis:

1. Gapet $e_{n}$ mellan de två ytorna måste vara noll (kontakt) eller strikt positivt (separation, $e_{n}>0$ );
2. Den normala spänningen $p_{n}$ som verkar på varje kropp är noll (separation) eller kompressiv ( $p_{n}>0$ i kontakt).

Matematiskt: $e_{n}\geq 0,p_{n}\geq 0,e_{n}\cdot p_{n}=0\,\ !$ . Här är $e_{n},p_{n}$ funktioner som varierar med läget längs kropparnas ytor.

I de tangentiella riktningarna används ofta följande villkor:

1. Den lokala (tangentiella) skjuvspänningen ${\vec {p}}=(p_{x},p_{y})^{\mathsf {T}}\, \!$ (förutsatt att normalriktningen är parallell med $z$ -axeln) kan inte överskrida ett visst positionsberoende maximum, den så kallade draggränsen $g$ ;
2. Där storleken på tangentiell dragkraft faller under dragkraftsgränsen ‖ $\displaystyle \|{\vec {p}}\|<g\,\!} ,$ fäster de motsatta ytorna ihop och mikroslip försvinner, ${\vec {s}}=(s_{x},s_{y})^{\mathsf {T}}={\vec {0} }\,\!$ ;
3. Mikroslip uppstår där de tangentiella dragningarna är vid dragkraftsgränsen; riktningen för den tangentiella dragningen är då motsatt riktningen för mikroslip ${\vec {p}}=-g{\vec {s}}/\ |{\vec {s}}\|\,\!$ .

Den exakta formen av dragkraften är den så kallade lokala friktionslagen. För detta tillämpas ofta Coulombs (globala) friktionslag lokalt: $\|{\vec {p}}\|\leq g=\mu p_{n}\,\ !$ , med $\mu$ friktionskoefficienten. Mer detaljerade formler är också möjliga, till exempel med $\mu$ beroende på temperatur $T$ , lokal glidhastighet $\|{\vec {s}}\|$ , etc.

Lösningar för statiska fall

Rep på en pollare, capstan-ekvationen

Illustration av ett elastiskt rep virat runt ett fast föremål som en pollare. Kontaktytan är uppdelad i stick- och glidzoner, beroende på belastningen på båda ändarna och på lasthistoriken.

Betrakta ett rep där lika krafter (t.ex. ${\displaystyle F_{\text{hold}}=400\,\mathrm {N} } )$ utövas på båda sidor. Genom detta sträcks repet lite och en inre spänning $T$ induceras ( $T=400\,\mathrm {N}$ på varje position längs repet). Repet lindas runt ett fast föremål såsom en pollare ; den böjs och kommer i kontakt med föremålets yta över en kontaktvinkel (t.ex. ${\displaystyle 180^{\circ }} )$ . Normalt tryck uppstår mellan repet och pollaren, men ingen friktion uppstår ännu. Därefter ökas kraften på ena sidan av pollaren till ett högre värde (t.ex. ${\displaystyle F_{\text{load}}=600\,\mathrm {N} } )$ . Detta orsakar friktionsskjuvspänningar i kontaktytan. I slutläget utövar pollaren en friktionskraft på repet så att en statisk situation uppstår.

Spänningsfördelningen i repet i den här slutliga situationen beskrivs av drevekvationen , med lösning:

${\begin{aligned}T(\phi )&=T_{\text{hold}},&\phi &\in \left[\phi _{\text{hold}},\phi _{ \text{intf}}\right]\\T(\phi )&=T_{\text{load}}e^{-\mu \phi },&\phi &\in \left[\phi _{\ text{intf}},\phi _{\text{load}}\right]\\\phi _{\text{intf}}&={\frac {1}{\mu }}\log \left({ \frac {T_{\text{load}}}{T_{\text{håll}}}}\right)&\end{aligned}}$

Spänningen ökar från $T_{\text{håll}}$ på den slaka sidan ( ${\displaystyle \phi =\phi _{\text{håll}}})$ till ${\ displaystyle T_{\text{load}}}$ på den övre sidan $\phi =\phi _{\text{load}}$ . Sett från den höga sidan sjunker spänningen exponentiellt tills den når den lägre belastningen vid $\phi =\phi _{\text{intf}}$ . Därefter är den konstant på detta värde. Övergångspunkten $\phi _{\text{intf}}$ bestäms av förhållandet mellan de två lasterna och friktionskoefficienten. Här är spänningarna $T$ i Newton och vinklarna $\phi$ i radianer.

Spänningen $T$ i repet i slutläget ökas i förhållande till initialtillståndet. Därför är repet förlängt något. Detta innebär att inte alla ytpartiklar i repet kan ha hållit sin utgångsposition på pollarens yta. Under lastningsprocessen gled repet en liten bit längs pollarens yta i glidområdet ϕ $\displaystyle \phi \in [\phi _{\text{intf}},\phi _ {\text{load}}]}$ . Denna glidning är precis tillräckligt stor för att komma till den förlängning som uppstår i sluttillståndet. Observera att det inte pågår någon glidning i sluttillståndet; termen glidarea avser den glidning som inträffade under lastningsprocessen. Observera vidare att platsen för glidområdet beror på initialtillståndet och lastningsprocessen. Om den initiala spänningen är $600\,\mathrm {N}$ och spänningen reduceras till $400\,\mathrm {N}$ på den slacka sidan, så inträffar glidområdet vid den slaka sidan av kontaktytan. För initialspänningar mellan $400$ och $600\,\mathrm {N}$ kan det finnas glidområden på båda sidor med ett stickområde emellan.

Generalisering för ett rep som ligger på en godtycklig ortotrop yta

Om ett rep ligger i jämvikt under tangentiella krafter på en grov ortotrop yta är tre följande villkor (alla) uppfyllda:

1. Ingen separation – normal reaktion $N$ är positiv för alla punkter på repkurvan:

   $N=-k_{n}T>0$ , där $k_ {n}$ är en normal krökning av repkurvan.

2. Dragfriktionskoefficient $\mu _{g}$ och vinkel $\alpha$ uppfyller följande kriterier för alla punkter på kurvan
   $-\mu _{g}<\tan \alpha <+\mu _{g}$
3. Gränsvärden för tangentialkrafterna:

   Krafterna i båda ändarna av repet $T$ och $T_{0}$ uppfyller följande olikhet

   $T_{0}e^{-\int _{s}\omega \mathrm {d} s}\leq T\leq T_ {0}e^{\int _{s}\omega \mathrm {d} s}$

   med $\omega =\mu _{\tau }{\sqrt {k_{ n}^{2}-{\frac {k_{g}^{2}}{\mu _{g}^{2}}}}}=\mu _{\tau}k{\sqrt {\cos ^{2}\alpha -{\frac {\sin ^{2}\alpha }{\mu _{g}^{2}}}}}$ ,

   där $k_{g}$ är en geodetisk krökning av repkurvan, $k$ är en krökning av en repkurva, $\mu _{\tau }$ är en koefficient friktion i tangentiell riktning.

   Om $\omega$$T_{0}e^{-\mu _{\tau }ks\,{\sqrt {\cos ^{2}\alpha -{\frac {\sin ^{2}\alpha }{\ mu _{g}^{2}}}}}}\leq T\leq T_{0}e^{\mu _{\tau }ks\,{\sqrt {\cos ^{2}\alpha -{ \frac {\sin ^{2}\alpha }{\mu _{g}^{2}}}}}}$ konstant så .

Denna generalisering har erhållits av Konyukhov A.,

Sfär på ett plan, (3D) Cattaneo-problemet

Betrakta en sfär som pressas på ett plan (halva utrymmet) och sedan flyttas över planets yta. Om sfären och planet idealiseras som stela kroppar, skulle kontakt uppstå i bara en enda punkt, och sfären skulle inte röra sig förrän den tangentiella kraften som appliceras når den maximala friktionskraften. Sedan börjar den glida över ytan tills den applicerade kraften minskar igen.

I verkligheten, med hänsyn till elastiska effekter, är situationen mycket annorlunda. Om en elastisk sfär pressas på ett elastiskt plan av samma material deformeras båda kropparna, en cirkulär kontaktyta uppstår och en (hertzisk) normal tryckfördelning uppstår. Sfärens centrum flyttas nedåt med ett avstånd $\delta _{n}$ som kallas inflygningen , vilket motsvarar den maximala penetrationen av de odeformerade ytorna. För en sfär med radie $R$ och elastiska konstanter $E,\nu$ lyder denna Hertzian-lösning:

${\begin{aligned}p_{n}(x,y)&=p_{0}{\sqrt {1-{\frac {r^{2} }{a^{2}}}}}&r&={\sqrt {x^{2}+y^{2}}}\leq a&a&={\sqrt {R\delta _{n}}}\\p_ {0}&={\frac {2}{\pi }}E^{*}{\sqrt {\frac {\delta _{n}}{R}}}&F_{n}&={\frac { 4}{3}}E^{*}{\sqrt {R}}\delta _{n}^{\frac {3}{2}}&E^{*}&={\frac {E}{2 \left(1-\nu ^{2}\right)}}\end{aligned}}$

Tänk nu på att en tangentiell kraft $F_{x}$ appliceras som är lägre än Coulombs friktionsgräns $\mu F_{n}$ . Centrum av sfären kommer då att flyttas i sidled med ett litet avstånd $\delta _{x}$ som kallas skiftet . En statisk jämvikt uppnås där elastiska deformationer uppstår samt friktionsskjuvspänningar i kontaktytan. I detta fall, om tangentialkraften reduceras, minskar även de elastiska deformationerna och skjuvspänningarna. Sfären skiftar till stor del tillbaka till sitt ursprungliga läge, förutom friktionsförluster som uppstår på grund av lokal glidning i kontaktlappen.

Detta kontaktproblem löstes ungefär av Cattaneo med hjälp av ett analytiskt tillvägagångssätt. Spänningsfördelningen i jämviktstillståndet består av två delar:

${\begin{aligned}p_{x}(x,y)&=\mu p_{0}\left({\sqrt {1-{\ frac {r^{2}}{a^{2}}}}}-{\frac {c}{a}}{\sqrt {1-{\frac {r^{2}}{c^{2 }}}}}\right)&0\leq {}&r\leq c\\p_{x}(x,y)&=\mu p_{n}(x,y)&c\leq {}&r\leq a \\p_{x}(x,y)&=0&a\leq {}&r\end{aligned}}$

I det centrala, stickande området $0\leq r\leq c$ förskjuts planets ytpartiklar över $u_{x}=\delta _{x }/2$ till höger medan sfärens ytpartiklar förskjuts över $u_{x}=-\delta _{x}/2$ åt vänster. Även om sfären som helhet rör sig över $\delta _{x}$ i förhållande till planet, rörde sig dessa ytpartiklar inte i förhållande till varandra. I den yttre ringen $c\leq r\leq r$ rörde sig ytpartiklarna i förhållande till varandra. Deras lokala skift erhålls som

$s_{x}(x,y)=\delta _{x}+u_{ x}^{\text{sfär}}(x,y)-u_{x}^{\text{plan}}(x,y)$

Denna förskjutning $s_{x}(x,y)$ är exakt så stor att en statisk jämvikt erhålls med skjuvspänningar vid dragkraften bunden i detta så kallade glidområde.

Så under den tangentiella belastningen av sfären sker partiell glidning . Kontaktytan delas alltså upp i ett glidområde där ytorna rör sig i förhållande till varandra och ett stickområde där de inte gör det. I jämviktstillståndet pågår ingen mer glidning.

Lösningar för dynamiska glidproblem

Lösningen av ett kontaktproblem består av tillståndet vid gränssnittet (där kontakten är, uppdelning av kontaktytan i stick- och glidzoner samt normal- och skjuvspänningsfördelningarna) plus det elastiska fältet i kropparnas inre. Denna lösning beror på kontaktens historik. Detta kan ses i förlängningen av Cattaneo-problemet som beskrivs ovan.

• I Cattaneo-problemet trycks sfären först på planet och förskjuts sedan tangentiellt. Detta ger partiell glidning såsom beskrivits ovan.
• Om sfären först förskjuts tangentiellt och sedan pressas mot planet, så finns det ingen tangentiell förskjutningsskillnad mellan de motstående ytorna och följaktligen finns det ingen tangentiell spänning i kontaktgränsytan.
• Om inflygningen i normal riktning och tangentiell förskjutning ökas samtidigt ("snedkompression") kan en situation uppnås med tangentiell spänning men utan lokal glidning.

Detta visar att tillståndet i kontaktgränssnittet inte bara är beroende av de två kropparnas relativa positioner, utan också på deras rörelsehistorik. Ett annat exempel på detta inträffar om sfären flyttas tillbaka till sin ursprungliga position. Initialt fanns ingen tangentiell spänning i kontaktgränssnittet. Efter det första skiftet har mikroslipning inträffat. Denna mikroslip blir inte helt ogiltig genom att växla tillbaka. Så i den slutliga situationen kvarstår tangentiella spänningar i gränssnittet, i vad som ser ut som en identisk konfiguration som den ursprungliga.

Inverkan av friktion på dynamiska kontakter (påverkan) beaktas i detalj i.

Lösning av rullande kontaktproblem

Rullande kontakt mellan en cylinder och ett plan. Partiklar som rör sig genom kontaktytan från höger till vänster, spänners mer och mer tills lokal glidning sätter in.

Rullande kontaktproblem är dynamiska problem där de kontaktande kropparna kontinuerligt rör sig i förhållande till varandra. En skillnad mot dynamiska glidkontaktproblem är att det finns mer variation i tillståndet för olika ytpartiklar. Medan kontaktlappen i ett glidproblem kontinuerligt består av mer eller mindre samma partiklar, kommer problempartiklar i en rullande kontakt in och lämnar kontaktlappen oavbrutet. I ett glidproblem utsätts dessutom alla ytpartiklarna i kontaktlappen för mer eller mindre samma tangentiella förskjutning överallt, medan ytpartiklarna i ett rullningsproblem belastas på ganska olika sätt. De är fria från stress när de går in i kontaktytan, fastnar sedan på en partikel på den motsatta ytan, spänns av den totala rörelseskillnaden mellan de två kropparna, tills den lokala dragkraftsgränsen överskrids och lokal glidning sätter in. olika stadier för olika delar av kontaktytan.

Om den totala rörelsen av kropparna är konstant, kan ett övergripande stabilt tillstånd uppnås. Här varierar tillståndet för varje ytpartikel i tid, men den totala fördelningen kan vara konstant. Detta formaliseras genom att använda ett koordinatsystem som rör sig tillsammans med kontaktlappen.

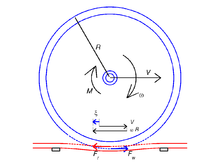
Cylinder som rullar på ett plan, (2D) Carter-Fromm-lösningen

Betrakta en cylinder som rullar över ett plan (halva rymden) under stabila förhållanden, med en tidsoberoende longitudinell krypning $\xi$ . (Relativt) långt borta från ändarna på cylindrarna uppstår en situation med plan töjning och problemet är tvådimensionellt.

Om cylindern och planet består av samma material är det normala kontaktproblemet opåverkat av skjuvspänningen. Kontaktytan är en remsa $x\in [-a,a]$ , och trycket beskrivs av (2D) Hertz-lösningen.

${\begin{aligned}p_{n}(x)&={\ frac {p_{0}}{a}}{\sqrt {a^{2}-x^{2}}}&|x|&\leq a&a^{2}&={\frac {4F_{n} R}{\pi E^{*}}}\\p_{0}&={\frac {2F_{n}}{\pi a}}&&&E^{*}&={\frac {E}{2 \left(1-\nu ^{2}\right)}}&\end{aligned}}$

Fördelningen av skjuvspänningen beskrivs av Carter-Fromm-lösningen. Den består av ett vidhäftningsområde vid kontaktytans framkant och ett glidområde vid bakkanten. Längden på vidhäftningsområdet betecknas $2a'$ . Vidare introduceras vidhäftningskoordinaten av $x'=x+aa'$ . I fallet med en positiv kraft $F_{x}>0$ (negativ krypning ${\displaystyle \xi <0} )$ är det:

${\begin{aligned}p_{x}(x)&=0&|&x|\geq a\\p_{x}(x)&={\frac {\mu p_{0} }{a}}\left({\sqrt {a^{2}-x^{2}}}-{\sqrt {a'^{2}-x'^{2}}}\right)&a- 2a'\leq {}&x\leq a\\p_{x}(x)&=\mu p_{n}(x)&&x\leq a-2a'\end{aligned}}$

Storleken på vidhäftningsytan beror på krypningen, hjulradien och friktionskoefficienten.

${\begin{aligned}a'&=a{\sqrt {1 -{\frac {|F_{x}|}{\mu F_{n}}}}},&{\mbox{för }}|F_{x}|\leq \mu F_{n}\\\xi &=-\operatörsnamn {tecken} (F_{x})\,{\frac {\mu (aa')}{R}},&{\mbox{ie }}|\xi |\leq {\frac { \mu a}{R}}\\F_{x}&=-\operatörsnamn {tecken} (\xi )\,\mu F_{n}\left(1-\left(1+{\frac {R| \xi |}{\mu a}}\right)^{2}\right)\end{aligned}}$

För större krypningar är $a'=0$ så att full glidning sker.

Halvutrymmesbaserade tillvägagångssätt

När man överväger kontaktproblem på de mellanliggande rumsliga skalorna, ignoreras de småskaliga materialets inhomogeniteter och ytjämnhet. Kropparna anses bestå av släta ytor och homogena material. En kontinuumansats används där spänningar, töjningar och förskjutningar beskrivs med (styckvis) kontinuerliga funktioner.

Halvutrymmesmetoden är en elegant lösningsstrategi för så kallade "slätkantade" eller "koncentrerade" kontaktproblem .

1. Om en massiv elastisk kropp belastas på en liten del av dess yta, dämpas de elastiska spänningarna proportionellt mot $1/distance^{2}$ och de elastiska förskjutningarna med $1/distance$ när man rör sig bort från denna yta.
2. Om en kropp inte har några skarpa hörn i eller nära kontaktområdet, så kan dess svar på en ytbelastning approximeras väl av svaret från ett elastiskt halvrum (t.ex. alla punkter ${ \displaystyle (x,y,z)^{\mathsf {T}}\in \mathbb {R} ^{3}\,\!} med$ z $\displaystyle z>0\,\!}$ ).
3. Det elastiska halvrumsproblemet löses analytiskt, se Boussinesq-Cerruti-lösningen .
4. På grund av linjäriteten i detta tillvägagångssätt kan flera dellösningar läggas över varandra.

Genom att använda den grundläggande lösningen för halvutrymmet reduceras det fullständiga 3D-kontaktproblemet till ett 2D-problem för kropparnas avgränsande ytor.

En ytterligare förenkling sker om de två kropparna är "geometriskt och elastiskt lika". I allmänhet inducerar stress inuti en kropp i en riktning också förskjutningar i vinkelräta riktningar. Följaktligen finns det en växelverkan mellan normalspänningen och tangentiella förskjutningar i kontaktproblemet, och en växelverkan mellan tangentiell spänning och normala förskjutningar. Men om den normala spänningen i kontaktgränsytan inducerar samma tangentiella förskjutningar i båda kontaktkropparna, så finns det ingen relativ tangentiell förskjutning av de två ytorna. I så fall är de normala och tangentiella kontaktproblemen frånkopplade. Om så är fallet kallas de två kropparna kvasiidentiska . Detta händer till exempel om kropparna är spegelsymmetriska med avseende på kontaktplanet och har samma elastiska konstanter.

Klassiska lösningar baserade på halvutrymmesmetoden är:

1. Hertz löste kontaktproblemet i frånvaro av friktion, för en enkel geometri (krökta ytor med konstanta krökningsradier).
2. Carter övervägde den rullande kontakten mellan en cylinder och ett plan, som beskrivits ovan. En komplett analytisk lösning tillhandahålls för den tangentiella dragkraften.
3. Cattaneo övervägde komprimeringen och förskjutningen av två sfärer, som beskrivits ovan. Observera att denna analytiska lösning är ungefärlig. I verkligheten förekommer små tangentiella dragningar $p_{y}$ som ignoreras.

Se även

• Adhesion railway – Järnväg som förlitar sig på adhesionsdragkraft för att flytta ett tåg
• Lager – Mekanism för att begränsa relativ rörelse till önskad rörelse och minska friktioner
• Kontaktmekanik – Studie av deformation av fasta ämnen som berör varandra
• (Linjär) elasticitet – Fysisk egenskap när material eller föremål återgår till ursprunglig form efter deformation
• Energetiskt modifierad cement – ​​Klass av cement, mekaniskt bearbetad för att omvandla reaktivitet
• Friktion – Kraft som motstår glidande rörelse
• Friktionsdrivning – Mekanisk kraftöverföring genom friktion mellan komponenter
• Smörjning – Närvaron av ett material för att minska friktionen mellan två ytor.
• Metallurgi – vetenskapsområde som studerar metallers fysiska och kemiska beteende
• Flerkroppssystem – Verktyg för att studera dynamiskt beteende hos sammankopplade stela eller flexibla kroppar
• Plasticitet – Icke-reversibel deformation av ett fast material som svar på applicerade krafter
• Valsning (metallbearbetning) – Metallformningsprocess
• Fast mekanik – En gren av mekanik som handlar om fasta material och deras beteenden
• Toroidformad eller rullbaserad CVT (Extroid CVT) – Transmissionsteknik för fordon
• Tribologi – Vetenskap och ingenjörskonst av interagerande ytor i relativ rörelse
• Fordonsdynamik – studiet av fordonsrörelseförändringar som svar på interaktion med förarens inmatningar, vägförhållanden och andra omgivningsförhållanden Sidor som visar wikidata-beskrivningar som en reserv
• Slitage – Skador, gradvis borttagning eller deformation av material på fasta ytor

externa länkar

• [1] Biografi om Prof.dr.ir. JJ Kalker (Tekniska universitetet i Delft).
• [2] Kalkers Hertzian/icke-Hertzian CONTACT-mjukvara.