Gas
| Del av en serie om |
| kontinuummekanik |
|---|
Gas är ett av materiens fyra grundläggande tillstånd . De andra är fasta , flytande och plasma .
En ren gas kan bestå av individuella atomer (t.ex. en ädelgas som neon ), elementära molekyler gjorda av en typ av atom (t.ex. syre ), eller sammansatta molekyler gjorda av en mängd olika atomer (t.ex. koldioxid ). En gasblandning , såsom luft , innehåller en mängd olika rena gaser. Det som skiljer en gas från vätskor och fasta ämnen är den stora separationen av de enskilda gaspartiklarna . Denna separation gör vanligtvis en färglös gas osynlig för den mänskliga observatören.
Materiens gasformiga tillstånd uppstår mellan vätske- och plasmatillståndet, varav det senare ger den övre temperaturgränsen för gaser. I den nedre delen av temperaturskalan ligger degenerativa kvantgaser som får allt större uppmärksamhet. Atomgaser med hög densitet underkylda till mycket låga temperaturer klassificeras enligt deras statistiska beteende som antingen Bose-gaser eller Fermi-gaser . För en omfattande lista över dessa exotiska tillstånd av materia, se listan över materiens tillstånd .
Elementära gaser
De enda kemiska grundämnena som är stabila diatomiska homonukleära molekylära gaser vid STP är väte (H 2 ), kväve (N 2 ), syre (O 2 ), och två halogener : fluor (F 2 ) och klor (Cl 2 ). När de grupperas tillsammans med de monoatomiska ädelgaserna – helium (He), neon (Ne), argon (Ar), krypton (Kr), xenon (Xe) och radon (Rn) – kallas dessa gaser för "elementargaser" .
Etymologi
Ordet gas användes först av den flamländska kemisten Jan Baptist van Helmont från början av 1600-talet . Han identifierade koldioxid , den första kända gasen förutom luft. Van Helmonts ord verkar helt enkelt ha varit en fonetisk transkription av det antika grekiska ordet χάος Chaos – g :et på nederländska uttalas som ch i "loch" (röstlös velarfrikativ, / x / ) – i vilket fall Van Helmont helt enkelt följde etablerat alkemiskt bruk som först intygades i Paracelsus verk . Enligt Paracelsus terminologi betydde kaos något i stil med "ultra-sällsynt vatten".
En alternativ historia är att Van Helmonts term härleddes från " gahst (eller geist ), som betyder ett spöke eller ande". Den berättelsen ges ingen trovärdighet av redaktörerna för Oxford English Dictionary . Däremot spekulerade den fransk-amerikanske historikern Jacques Barzun att Van Helmont hade lånat ordet från tyskan Gäscht , vilket betyder skummet som härrör från jäsning .
Fysiska egenskaper
Eftersom de flesta gaser är svåra att observera direkt, beskrivs de genom användning av fyra fysikaliska egenskaper eller makroskopiska egenskaper: tryck , volym , antal partiklar (kemister grupperar dem efter mol ) och temperatur. Dessa fyra egenskaper observerades upprepade gånger av forskare som Robert Boyle , Jacques Charles , John Dalton , Joseph Gay-Lussac och Amedeo Avogadro för en mängd olika gaser i olika miljöer. Deras detaljerade studier ledde slutligen till ett matematiskt samband mellan dessa egenskaper uttryckt av den ideala gaslagen (se avsnittet om förenklade modeller nedan).
Gaspartiklar är vitt separerade från varandra och har följaktligen svagare intermolekylära bindningar än vätskor eller fasta ämnen. Dessa intermolekylära krafter är resultatet av elektrostatiska interaktioner mellan gaspartiklar. Liknande laddade områden av olika gaspartiklar stöter bort, medan motsatt laddade områden av olika gaspartiklar attraherar varandra; gaser som innehåller permanent laddade joner kallas plasma . Gasformiga föreningar med polära kovalenta bindningar innehåller permanenta laddningsobalanser och upplever därför relativt starka intermolekylära krafter, även om molekylen medan föreningens nettoladdning förblir neutral. Övergående, slumpmässigt inducerade laddningar existerar över icke-polära kovalenta bindningar av molekyler och elektrostatiska interaktioner orsakade av dem kallas Van der Waals-krafter . Interaktionen mellan dessa intermolekylära krafter varierar inom ett ämne, vilket bestämmer många av de fysiska egenskaperna som är unika för varje gas. En jämförelse av kokpunkter för föreningar bildade av joniska och kovalenta bindningar leder oss till denna slutsats. De drivande rökpartiklarna i bilden ger en viss inblick i lågtrycksgasens beteende.
Jämfört med andra materiatillstånd har gaser låg densitet och viskositet . Tryck och temperatur påverkar partiklarna inom en viss volym. Denna variation i partikelseparation och hastighet kallas kompressibilitet . Denna partikelseparation och storlek påverkar optiska egenskaper hos gaser som kan hittas i följande lista över brytningsindex . Slutligen sprids gaspartiklar isär eller diffunderar för att homogent fördela sig genom vilken behållare som helst.
Makroskopisk bild av gaser
När man observerar en gas är det typiskt att ange en referensram eller längdskala . En större längdskala motsvarar en makroskopisk eller global synvinkel för gasen. Denna region (refererad till som en volym) måste vara tillräckligt stor för att innehålla ett stort prov av gaspartiklar. Den resulterande statistiska analysen av denna provstorlek ger det "genomsnittliga" beteendet (dvs hastighet, temperatur eller tryck) för alla gaspartiklar i området. Däremot motsvarar en mindre längdskala en mikroskopisk eller partikelsynpunkt.
Makroskopiskt är de gasegenskaper som mäts antingen i termer av själva gaspartiklarna (hastighet, tryck eller temperatur) eller deras omgivning (volym). Till exempel studerade Robert Boyle pneumatisk kemi under en liten del av sin karriär. Ett av hans experiment relaterade de makroskopiska egenskaperna hos tryck och volym hos en gas. Hans experiment använde en J-rörsmanometer som ser ut som ett provrör i form av bokstaven J. Boyle fångade en inert gas i den stängda änden av provröret med en kolonn av kvicksilver , vilket gjorde antalet partiklar och temperaturen konstant. Han observerade att när trycket ökades i gasen, genom att tillsätta mer kvicksilver till kolonnen, minskade den fångade gasens volym (detta är känt som ett omvänt förhållande). Dessutom, när Boyle multiplicerade trycket och volymen för varje observation, produkten konstant. Detta förhållande gällde för varje gas som Boyle observerade ledde till lagen, (PV=k), uppkallad för att hedra hans arbete inom detta område.
Det finns många matematiska verktyg tillgängliga för att analysera gasegenskaper. När gaser utsätts för extrema förhållanden blir dessa verktyg mer komplexa, från Euler-ekvationerna för inviscid flöde till Navier-Stokes-ekvationerna som fullt ut står för viskösa effekter. Dessa ekvationer är anpassade till förhållandena i gassystemet i fråga. Boyles labbutrustning gjorde det möjligt att använda algebra för att få sina analytiska resultat. Hans resultat var möjliga eftersom han studerade gaser i relativt lågtryckssituationer där de betedde sig på ett "idealiskt" sätt. Dessa idealiska förhållanden gäller för säkerhetsberäkningar för en mängd olika flygförhållanden på materialen som används. Den högteknologiska utrustningen som används idag har utformats för att hjälpa oss att säkert utforska de mer exotiska driftsmiljöerna där gaserna inte längre beter sig på ett "idealiskt" sätt. Denna avancerade matematik, inklusive statistik och multivariabel kalkyl , möjliggör lösningen på så komplexa dynamiska situationer som rymdfarkoster återinträde. Ett exempel är analysen av rymdfärjans återinträde på bilden för att säkerställa att materialegenskaperna under detta belastningstillstånd är lämpliga. I denna flygregim beter sig gasen inte längre idealiskt.
Tryck
Symbolen som används för att representera tryck i ekvationer är "p" eller "P" med SI-enheter av pascal .
När man beskriver en gasbehållare avser termen tryck (eller absolut tryck) den genomsnittliga kraft per ytenhet som gasen utövar på behållarens yta. Inom denna volym är det ibland lättare att visualisera gaspartiklarna som rör sig i raka linjer tills de kolliderar med behållaren (se diagram överst i artikeln). Kraften som överförs av en gaspartikel till behållaren under denna kollision är förändringen i partikelns rörelsemängd . Under en kollision ändras endast den normala komponenten av hastigheten. En partikel som rör sig parallellt med väggen ändrar inte dess rörelsemängd. Därför måste medelkraften på en yta vara den genomsnittliga förändringen i linjärt rörelsemängd från alla dessa gaspartikelkollisioner.
Tryck är summan av alla normala kraftkomponenter som utövas av partiklarna som träffar behållarens väggar dividerat med väggens yta.
Temperatur
Symbolen som används för att representera temperaturen i ekvationer är T med SI-enheter av kelvin .
Hastigheten hos en gaspartikel är proportionell mot dess absoluta temperatur . Ballongens volym i videon krymper när de fångade gaspartiklarna saktar ner med tillsats av extremt kallt kväve. Temperaturen i alla fysiska system är relaterad till rörelserna hos partiklarna (molekyler och atomer) som utgör [gas]systemet. I statistisk mekanik är temperatur måttet på den genomsnittliga kinetiska energin som lagras i en molekyl (även känd som termisk energi). Metoderna för att lagra denna energi dikteras av frihetsgraderna för själva molekylen ( energilägen) . Termisk (kinetisk) energi tillsatt till en gas eller vätska (en endoterm process) producerar translations-, rotations- och vibrationsrörelse. Däremot kan ett fast ämne bara öka sin inre energi genom att spännande ytterligare vibrationslägen, eftersom kristallgitterstrukturen förhindrar både translations- och rotationsrörelse. Dessa uppvärmda gasmolekyler har ett större hastighetsområde (vidare fördelning av hastigheter) med en högre medel- eller medelhastighet . Variansen i denna fördelning beror på att hastigheterna hos enskilda partiklar ständigt varierar, på grund av upprepade kollisioner med andra partiklar. Hastighetsområdet kan beskrivas av Maxwell–Boltzmann-fördelningen . Användning av denna fördelning innebär idealiska gaser nära termodynamisk jämvikt för det system av partiklar som övervägs.
Specifik volym
Symbolen som används för att representera specifik volym i ekvationer är "v" med SI-enheter av kubikmeter per kilogram.
Symbolen som används för att representera volym i ekvationer är "V" med SI-enheter av kubikmeter.
När man utför en termodynamisk analys är det typiskt att tala om intensiva och omfattande egenskaper . Egenskaper som beror på mängden gas (antingen i massa eller volym) kallas extensiva egenskaper, medan egenskaper som inte är beroende av mängden gas kallas intensiva egenskaper. Specifik volym är ett exempel på en intensiv egenskap eftersom det är förhållandet mellan volymen som upptas av en massaenhet av en gas som är identisk i hela systemet vid jämvikt. 1000 atomer en gas upptar samma utrymme som alla andra 1000 atomer för en given temperatur och tryck. Detta koncept är lättare att visualisera för fasta ämnen som järn som är inkompressibla jämfört med gaser. Men volymen i sig --- inte specifik --- är en omfattande egenskap.
Densitet
Symbolen som används för att representera densitet i ekvationer är ρ (rho) med SI-enheter av kilogram per kubikmeter. Denna term är den ömsesidiga av specifik volym.
Eftersom gasmolekyler kan röra sig fritt i en behållare kännetecknas deras massa normalt av densitet. Densitet är mängden massa per volymenhet av ett ämne, eller det omvända till specifik volym. För gaser kan densiteten variera över ett brett område eftersom partiklarna är fria att röra sig närmare varandra när de begränsas av tryck eller volym. Denna variation av densitet kallas kompressibilitet . Liksom tryck och temperatur är densitet en tillståndsvariabel för en gas och förändringen i densitet under varje process styrs av termodynamikens lagar. För en statisk gas är densiteten densamma i hela behållaren. Densitet är därför en skalär storhet . Det kan visas genom kinetisk teori att densiteten är omvänt proportionell mot storleken på behållaren i vilken en fast massa gas är innesluten. I detta fall av en fast massa minskar densiteten när volymen ökar.
Mikroskopisk bild av gaser
Om man kunde observera en gas under ett kraftfullt mikroskop skulle man se en samling partiklar utan någon bestämd form eller volym som är i mer eller mindre slumpmässig rörelse. Dessa gaspartiklar ändrar endast riktning när de kolliderar med en annan partikel eller med behållarens sidor. Denna mikroskopiska syn på gas är väl beskriven av statistisk mekanik , men den kan beskrivas av många olika teorier. Den kinetiska teorin om gaser , som gör antagandet att dessa kollisioner är perfekt elastiska , tar inte hänsyn till intermolekylära krafter av attraktion och repulsion.
Kinetisk teori om gaser
Kinetisk teori ger insikt i de makroskopiska egenskaperna hos gaser genom att beakta deras molekylära sammansättning och rörelse. Från och med definitionerna av rörelsemängd och kinetisk energi kan man använda bevarandet av rörelsemängd och geometriska samband för en kub för att relatera makroskopiska systemegenskaper för temperatur och tryck till den mikroskopiska egenskapen hos kinetisk energi per molekyl. Teorin ger medelvärden för dessa två egenskaper.
Den kinetiska teorin om gaser kan hjälpa till att förklara hur systemet (samlingen av gaspartiklar som övervägs) reagerar på förändringar i temperatur, med en motsvarande förändring i kinetisk energi .
Till exempel: Föreställ dig att du har en förseglad behållare av fast storlek (en konstant volym), som innehåller ett fast antal gaspartiklar; utgående från absoluta nollpunkten (den teoretiska temperaturen vid vilken atomer eller molekyler inte har någon termisk energi, dvs inte rör sig eller vibrerar), börjar man tillföra energi till systemet genom att värma upp behållaren, så att energi överförs till partiklarna inuti. När deras inre energi är över nollpunktsenergin , vilket betyder att deras kinetiska energi (även känd som termisk energi ) inte är noll, kommer gaspartiklarna att börja röra sig runt behållaren. När lådan värms upp ytterligare (eftersom mer energi tillförs), ökar de enskilda partiklarna sin medelhastighet när systemets totala interna energi ökar. Den högre medelhastigheten för alla partiklar leder till en högre hastighet med vilken kollisioner sker (dvs. större antal kollisioner per tidsenhet), mellan partiklar och behållaren, såväl som mellan partiklarna själva.
Den makroskopiska , mätbara mängden tryck är det direkta resultatet av dessa mikroskopiska partikelkollisioner med ytan, över vilka enskilda molekyler utövar en liten kraft, var och en bidrar till den totala kraft som appliceras inom ett specifikt område. ( Läs " Tryck " i avsnittet " Makroskopisk bild av gaser " ovan.)
Likaså är den makroskopiskt mätbara kvantiteten temperatur en kvantifiering av den totala mängden rörelse, eller kinetisk energi som partiklarna uppvisar. ( Läs " Temperatur " i avsnittet " Makroskopisk bild av gaser " ovan.)
Termisk rörelse och statistisk mekanik
I den kinetiska teorin om gaser antas kinetisk energi enbart bestå av linjära translationer enligt en hastighetsfördelning av partiklar i systemet. Men i verkliga gaser och andra verkliga ämnen är rörelserna som definierar den kinetiska energin i ett system (som tillsammans bestämmer temperaturen), mycket mer komplexa än enkel linjär translation på grund av den mer komplexa strukturen hos molekyler, jämfört med enskilda atomer som agera på samma sätt som punktmassor . I verkliga termodynamiska system spelar kvantfenomen en stor roll för att bestämma termiska rörelser. De slumpmässiga, termiska rörelserna (kinetisk energi) i molekyler är en kombination av en ändlig uppsättning möjliga rörelser inklusive translation, rotation och vibration . Detta ändliga intervall av möjliga rörelser, tillsammans med den ändliga uppsättningen av molekyler i systemet, leder till ett ändligt antal mikrotillstånd inom systemet; vi kallar mängden av alla mikrotillstånd för en ensemble . Specifikt för atomära eller molekylära system kan vi potentiellt ha tre olika typer av ensemble, beroende på situationen: mikrokanonisk ensemble , kanonisk ensemble eller grand canonical ensemble . Specifika kombinationer av mikrotillstånd inom en ensemble är hur vi verkligen definierar systemets makrotillstånd (temperatur, tryck, energi, etc.). För att göra det måste vi först räkna alla mikrotillstånd genom användning av en partitionsfunktion . Användningen av statistisk mekanik och partitionsfunktionen är ett viktigt verktyg genom hela fysikalisk kemi, eftersom det är nyckeln till kopplingen mellan de mikroskopiska tillstånden i ett system och de makroskopiska variablerna som vi kan mäta, såsom temperatur, tryck, värmekapacitet , intern energi, entalpi och entropi, bara för att nämna några. ( Läs : Partitionsfunktion Betydelse och betydelse )
Att använda partitionsfunktionen för att hitta energin hos en molekyl, eller ett system av molekyler, kan ibland approximeras med Equipartition theorem , som i hög grad förenklar beräkningen. Denna metod förutsätter dock att alla molekylära frihetsgrader är lika befolkade och därför lika utnyttjade för att lagra energi i molekylen. Det skulle innebära att intern energi förändras linjärt med temperaturen, vilket inte är fallet. Detta bortser från det faktum att värmekapaciteten förändras med temperaturen, på grund av att vissa frihetsgrader är otillgängliga (aka "frusen ut") vid lägre temperaturer. När den inre energin hos molekyler ökar, ökar också förmågan att lagra energi inom ytterligare frihetsgrader. När fler frihetsgrader blir tillgängliga för att hålla energi, gör detta att ämnets molära värmekapacitet ökar.

Brownsk rörelse
Brownsk rörelse är den matematiska modellen som används för att beskriva den slumpmässiga rörelsen av partiklar suspenderade i en vätska. Gaspartikelanimeringen, med rosa och gröna partiklar, illustrerar hur detta beteende leder till att gaser sprids ( entropi ). Dessa händelser beskrivs också av partikelteorin .
Eftersom det är på gränsen för (eller bortom) nuvarande teknologi att observera enskilda gaspartiklar (atomer eller molekyler), ger endast teoretiska beräkningar förslag på hur de rör sig, men deras rörelse skiljer sig från Brownsk rörelse eftersom Brownsk rörelse innebär en jämn motstånd pga. till friktionskraften hos många gasmolekyler, avbruten av våldsamma kollisioner mellan en enskild (eller flera) gasmolekyl(er) med partikeln. Partikeln (som vanligen består av miljoner eller miljarder atomer) rör sig alltså i en taggig kurs, men ändå inte så taggig som man skulle förvänta sig om en enskild gasmolekyl undersöktes.
Intermolekylära krafter - den primära skillnaden mellan verkliga och idealiska gaser
Krafter mellan två eller flera molekyler eller atomer, antingen attraktiva eller frånstötande, kallas intermolekylära krafter . Intermolekylära krafter upplevs av molekyler när de befinner sig i fysisk närhet av varandra. Dessa krafter är mycket viktiga för att korrekt modellera molekylära system, för att exakt förutsäga det mikroskopiska beteendet hos molekyler i alla system, och är därför nödvändiga för att exakt förutsäga de fysikaliska egenskaperna hos gaser (och vätskor) över stora variationer i fysiska förhållanden.
En av de mest framträdande intermolekylära krafterna genom hela fysiken, som härrör från studiet av fysikalisk kemi , är van der Waals krafter . Van der Waals krafter spelar en nyckelroll för att bestämma nästan alla fysiska egenskaper hos vätskor som viskositet , flödeshastighet och gasdynamik (se avsnittet om fysiska egenskaper). Van der Waals interaktioner mellan gasmolekyler är anledningen till att modellering av en "riktig gas" är mer matematiskt svårare än en " ideal gas". Genom att ignorera dessa närhetsberoende krafter kan en riktig gas behandlas som en idealgas , vilket avsevärt förenklar beräkningen.
De intermolekylära attraktionerna och repulsionerna mellan två gasmolekyler är beroende av hur långt avståndet är mellan dem. De kombinerade attraktionerna och repulsionerna är väl modellerade av Lennard-Jones potentialen , som är en av de mest omfattande studerade av alla interatomära potentialer som beskriver den potentiella energin i molekylära system. Lennard-Jones potentialen mellan molekyler kan delas upp i två separata komponenter: en långdistansattraktion på grund av Londons dispersionskraft och en kortdistansrepulsion på grund av elektron-elektronutbytesinteraktion ( vilket är relaterat till Paulis uteslutningsprincip ).
När två molekyler är relativt avlägsna (vilket betyder att de har en hög potentiell energi), upplever de en svag attraktionskraft, vilket får dem att röra sig mot varandra, vilket sänker deras potentiella energi. Men om molekylerna är för långt borta, skulle de inte uppleva attraktionskraft av någon betydelse. Dessutom, om molekylerna kommer för nära kommer de att kollidera och uppleva en mycket hög repulsiv kraft (modellerad av hårda sfärer ) vilket är en mycket starkare kraft än attraktionerna, så att all attraktion på grund av närhet bortses från.
När två molekyler närmar sig varandra, från ett avstånd som varken är för långt eller för nära, ökar deras attraktion när storleken på deras potentiella energi ökar (blir mer negativ) och sänker deras totala inre energi. Attraktionen som får molekylerna att komma närmare kan bara ske om molekylerna förblir i närheten under den tid det tar att fysiskt röra sig närmare. Därför är attraktionskrafterna starkast när molekylerna rör sig i låga hastigheter . Det betyder att attraktionen mellan molekyler är betydande när gastemperaturen är låg . Men om du skulle isotermiskt komprimera denna kalla gas till en liten volym, tvingar molekylerna in i närheten och höjer trycket, kommer avstötningarna att börja dominera över attraktionerna, eftersom hastigheten med vilken kollisioner sker kommer att öka avsevärt. Därför, vid låga temperaturer och låga tryck, attraktion den dominerande intermolekylära interaktionen.
Om två molekyler rör sig med höga hastigheter, i godtyckliga riktningar, längs icke-korsande vägar, kommer de inte att tillbringa tillräckligt med tid i närheten för att påverkas av den attraktiva London-spridningskraften. Om de två molekylerna kolliderar rör sig de för snabbt och deras kinetiska energi kommer att vara mycket större än någon attraktiv potentiell energi, så de kommer bara att uppleva avstötning när de kolliderar. Således kan attraktioner mellan molekyler försummas vid höga temperaturer på grund av höga hastigheter. Vid höga temperaturer och höga tryck repulsion den dominerande intermolekylära interaktionen.
Redogörelse för de ovan angivna effekterna som orsakar dessa attraktioner och avstötningar, verkliga gaser , avgränsas från den ideala gasmodellen genom följande generalisering:
- Vid låga temperaturer och låga tryck är volymen som upptas av en riktig gas mindre än volymen som förutsägs av den ideala gaslagen.
- Vid höga temperaturer och höga tryck är volymen som upptas av en verklig gas större än volymen som förutsägs av den ideala gaslagen.
Matematiska modeller
En tillståndsekvation (för gaser) är en matematisk modell som används för att grovt beskriva eller förutsäga en gass tillståndsegenskaper. För närvarande finns det ingen enskild tillståndsekvation som exakt förutsäger egenskaperna hos alla gaser under alla förhållanden. Därför har ett antal mycket mer exakta tillståndsekvationer utvecklats för gaser i specifika temperatur- och tryckområden. De "gasmodeller" som diskuteras mest är "perfekt gas", "idealgas" och "riktig gas". Var och en av dessa modeller har sin egen uppsättning antaganden för att underlätta analysen av ett givet termodynamiskt system. Varje efterföljande modell utökar temperaturområdet för täckning som den gäller.
Perfekt och perfekt gas
Tillståndsekvationen för en ideal eller perfekt gas är den ideala gaslagen och lyder
där P är trycket, V är volymen, n är mängden gas (i molenheter), R är den universella gaskonstanten , 8,314 J/(mol K), och T är temperaturen. Skrivet på detta sätt kallas det ibland för "kemistversionen", eftersom det betonar antalet molekyler n . Det kan också skrivas som
där är den specifika gaskonstanten för en viss gas, i enheter J/(kg K), och ρ = m/V är densitet. Denna notation är "gasdynamistens" version, som är mer praktisk vid modellering av gasflöden som involverar acceleration utan kemiska reaktioner.
Den ideala gaslagen gör inte ett antagande om en gass specifika värme. I det mest allmänna fallet är den specifika värmen en funktion av både temperatur och tryck. Om tryckberoendet försummas (och möjligen även temperaturberoendet) i en viss tillämpning, sägs ibland gasen vara en perfekt gas , även om de exakta antagandena kan variera beroende på författare och/eller vetenskapsområde.
För en idealgas gäller idealgaslagen utan begränsningar för den specifika värmen. En idealgas är en förenklad "riktig gas" med antagandet att kompressibilitetsfaktorn Z är satt till 1 vilket betyder att detta pneumatiska förhållande förblir konstant. En kompressibilitetsfaktor på en kräver också att de fyra tillståndsvariablerna följer den ideala gaslagen .
Denna approximation är mer lämpad för applikationer inom teknik även om enklare modeller kan användas för att skapa en "bollpark"-serie om var den verkliga lösningen ska ligga. Ett exempel där den "ideala gasapproximationen" skulle vara lämplig skulle vara inuti en förbränningskammare i en jetmotor . Det kan också vara användbart att behålla elementära reaktioner och kemiska dissociationer för att beräkna utsläppen .
Riktig gas

Vart och ett av antagandena nedan bidrar till komplexiteten i problemets lösning. När densiteten hos en gas ökar med stigande tryck, spelar de intermolekylära krafterna en mer betydande roll i gasens beteende, vilket resulterar i att den ideala gaslagen inte längre ger "rimliga" resultat. I den övre delen av motortemperaturområdena (t.ex. brännkammare – 1300 K) absorberar de komplexa bränslepartiklarna inre energi genom rotationer och vibrationer som gör att deras specifika värme varierar från diatomiska molekyler och ädelgaser. Vid mer än dubbelt så hög temperatur börjar elektronisk excitation och dissociation av gaspartiklarna ske vilket gör att trycket anpassas till ett större antal partiklar (övergång från gas till plasma ). Slutligen antogs alla termodynamiska processer beskriva enhetliga gaser vars hastigheter varierade enligt en fast fördelning. Att använda en icke-jämviktssituation innebär att flödesfältet måste karakteriseras på något sätt för att möjliggöra en lösning. Ett av de första försöken att utvidga gränserna för den ideala gaslagen var att inkludera täckning för olika termodynamiska processer genom att justera ekvationen för att läsa pV n = konstant och sedan variera n genom olika värden såsom det specifika värmeförhållandet , γ .
Verkliga gaseffekter inkluderar de justeringar som gjorts för att ta hänsyn till ett större spektrum av gasbeteende:
- Kompressibilitetseffekter ( Z får variera från 1,0)
- Variabel värmekapacitet (specifik värme varierar med temperaturen)
- Van der Waals krafter (relaterade till kompressibilitet, kan ersätta andra tillståndsekvationer)
- Termodynamiska effekter utan jämvikt
- Frågor med molekylär dissociation och elementära reaktioner med variabel sammansättning.
För de flesta tillämpningar är en sådan detaljerad analys överdriven. Exempel där verkliga gaseffekter skulle ha en betydande inverkan skulle vara på rymdfärjans återinträde där extremt höga temperaturer och tryck förekom eller de gaser som producerades under geologiska händelser som i bilden av utbrottet av Mount Redoubt 1990 .
Permanent gas
Permanent gas är en term som används för en gas som har en kritisk temperatur under intervallet för normala människors beboeliga temperaturer och därför inte kan göras flytande genom tryck inom detta intervall. Historiskt ansågs sådana gaser vara omöjliga att göra flytande och skulle därför permanent förbli i gasformigt tillstånd. Termen är relevant för lagring i omgivningstemperatur och transport av gaser vid högt tryck.
Historisk forskning
Boyles lag
Boyles lag var kanske det första uttrycket för en statsekvation. 1662 Robert Boyle en serie experiment med ett J-format glasrör, som var förseglat i ena änden. Kvicksilver tillsattes till röret, vilket fångade en bestämd mängd luft i den korta, förseglade änden av röret. Sedan mättes gasvolymen noggrant när ytterligare kvicksilver tillsattes röret. Gasens tryck kunde bestämmas av skillnaden mellan kvicksilvernivån i den korta änden av röret och den i den långa, öppna änden. Bilden av Boyles utrustning visar några av de exotiska verktyg som Boyle använde under hans studie av gaser.
Genom dessa experiment noterade Boyle att trycket som utövas av en gas som hålls vid en konstant temperatur varierar omvänt med gasens volym. Till exempel, om volymen halveras, fördubblas trycket; och om volymen fördubblas halveras trycket. Givet det omvända förhållandet mellan tryck och volym är produkten av tryck ( P ) och volym ( V ) en konstant ( k ) för en given massa av innesluten gas så länge som temperaturen är konstant. Angivet som en formel är alltså:
Eftersom före- och eftervolymerna och trycken för den fasta mängden gas, där före- och eftertemperaturerna är desamma båda lika med konstanten k , kan de relateras med ekvationen:
Charles lag
År 1787 fann den franske fysikern och ballongpionjären Jacques Charles att syre, kväve, väte, koldioxid och luft expanderar i samma utsträckning över samma 80 kelvin-intervall. Han noterade att för en idealisk gas vid konstant tryck är volymen direkt proportionell mot dess temperatur:
Gay-Lussacs lag
1802 publicerade Joseph Louis Gay-Lussac resultat av liknande, men mer omfattande experiment. Gay-Lussac krediterade Charles tidigare arbete genom att namnge lagen till hans ära. Gay-Lussac själv är krediterad för lagen som beskriver trycket, som han fann 1809. Den säger att trycket som utövas på en containers sidor av en idealgas är proportionell mot dess temperatur.
Avogadros lag
1811 verifierade Amedeo Avogadro att lika volymer rena gaser innehåller samma antal partiklar. Hans teori var inte allmänt accepterad förrän 1858 när en annan italiensk kemist Stanislao Cannizzaro kunde förklara icke-ideala undantag. För hans arbete med gaser ett århundrade tidigare är den fysiska konstanten som bär hans namn ( Avogadro-konstanten ) antalet atomer per mol elementärt kol-12 ( 6,022 × 10 23 mol −1 ). Detta specifika antal gaspartiklar, vid standardtemperatur och -tryck (ideal gaslag) upptar 22,40 liter, vilket kallas den molära volymen .
Avogadros lag säger att volymen som upptas av en idealgas är proportionell mot mängden ämne i volymen. Detta ger upphov till den molära volymen av en gas, som vid STP är 22,4 dm 3 /mol (liter per mol). Relationen ges av
Daltons lag

År 1801 publicerade John Dalton lagen om partialtryck från sitt arbete med idealt gaslagsförhållande: Trycket hos en blandning av icke-reaktiva gaser är lika med summan av trycken för alla de ingående gaserna enbart. Matematiskt kan detta representeras för n arter som:
- Tryck totalt = Tryck 1 + Tryck 2 + ... + Tryck n
Bilden av Daltons dagbok visar symbologi som han använde som stenografi för att registrera vägen han följde. Bland hans viktiga journalobservationer vid blandning av oreaktiva "elastiska vätskor" (gaser) var följande:
- Till skillnad från vätskor, drev inte tyngre gaser till botten vid blandning.
- Gaspartikelidentitet spelade ingen roll för att bestämma sluttrycket (de uppförde sig som om deras storlek var försumbar).
Särskilda ämnen
Kompressibilitet
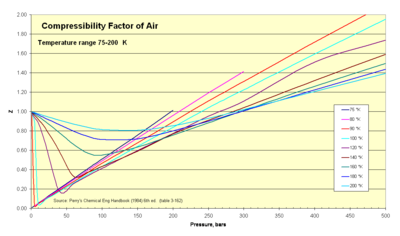
Termodynamiker använder denna faktor ( Z ) för att ändra den ideala gasekvationen för att ta hänsyn till kompressibilitetseffekter av verkliga gaser. Denna faktor representerar förhållandet mellan faktiska och idealiska specifika volymer. Det kallas ibland för en "fudge-faktor" eller korrigering för att utöka det användbara området för den ideala gaslagen för designändamål. Vanligtvis är detta Z -värde mycket nära enhet. Kompressibilitetsfaktorbilden illustrerar hur Z varierar över ett område av mycket kalla temperaturer.
Reynolds nummer
Inom vätskemekanik är Reynolds-talet förhållandet mellan tröghetskrafter ( v s ρ ) och viskösa krafter ( μ/L) . Det är ett av de viktigaste dimensionslösa talen inom vätskedynamik och används, vanligtvis tillsammans med andra dimensionslösa tal, för att tillhandahålla ett kriterium för att bestämma dynamisk liknelse. Som sådan ger Reynolds-numret länken mellan modelleringsresultat (design) och de faktiska förhållandena i full skala. Den kan också användas för att karakterisera flödet.
Viskositet
Viskositet, en fysisk egenskap, är ett mått på hur väl intilliggande molekyler håller fast vid varandra. En fast substans kan motstå en skjuvkraft på grund av styrkan hos dessa klibbiga intermolekylära krafter. En vätska kommer kontinuerligt att deformeras när den utsätts för en liknande belastning. Medan en gas har ett lägre viskositetsvärde än en vätska, är det fortfarande en observerbar egenskap. Om gaser inte hade någon viskositet, skulle de inte fastna på ytan av en vinge och bilda ett gränsskikt. En studie av deltavingen i Schlieren -bilden visar att gaspartiklarna fastnar vid varandra (se avsnittet Gränsskikt).
Turbulens

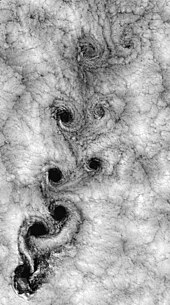
Inom vätskedynamik är turbulens eller turbulent flöde en flödesregim som kännetecknas av kaotiska, stokastiska egenskapsförändringar. Detta inkluderar låg momentumdiffusion, hög momentumkonvektion och snabb variation av tryck och hastighet i rum och tid. Satellitvyn över vädret runt Robinson Crusoe Islands illustrerar ett exempel.
Gränsskikt
Partiklar kommer i själva verket att "fastna" på ytan av ett föremål som rör sig genom det. Detta lager av partiklar kallas gränsskiktet. Vid föremålets yta är den i huvudsak statisk på grund av ytans friktion. Objektet, med dess gränsskikt, är i praktiken den nya formen på objektet som resten av molekylerna "ser" när objektet närmar sig. Detta gränsskikt kan separeras från ytan, i huvudsak skapa en ny yta och helt förändra flödesvägen. Det klassiska exemplet på detta är en vingprofil . Deltavingebilden visar tydligt gränsskiktets förtjockning när gasen strömmar från höger till vänster längs framkanten.
Maximal entropiprincip
När det totala antalet frihetsgrader närmar sig oändligheten, kommer systemet att hittas i det makrotillstånd som motsvarar den högsta multipliciteten . För att illustrera denna princip, observera hudtemperaturen på en frusen metallstång. Använd en termisk bild av hudtemperaturen och notera temperaturfördelningen på ytan. Denna initiala observation av temperaturen representerar ett " mikrotillstånd ". Vid någon framtida tidpunkt producerar en andra observation av hudtemperaturen ett andra mikrotillstånd. Genom att fortsätta denna observationsprocess är det möjligt att producera en serie mikrotillstånd som illustrerar den termiska historien för stångens yta. Karakterisering av denna historiska serie av mikrotillstånd är möjlig genom att välja den makrotillstånd som framgångsrikt klassificerar dem alla i en enda grupp.
Termodynamisk jämvikt
När energiöverföringen upphör från ett system kallas detta tillstånd för termodynamisk jämvikt. Vanligtvis innebär detta tillstånd att systemet och omgivningen har samma temperatur så att värme inte längre överförs mellan dem. Det innebär också att yttre krafter är balanserade (volymen ändras inte), och alla kemiska reaktioner inom systemet är fullständiga. Tidslinjen varierar för dessa händelser beroende på vilket system det gäller. En behållare med is som tillåts smälta vid rumstemperatur tar timmar, medan i halvledare kan värmeöverföringen som sker i enhetens övergång från ett tillstånd till avstängt vara i storleksordningen några nanosekunder.
|
Till
Från
|
Fast | Flytande | Gas | Plasma |
|---|---|---|---|---|
| Fast | Smältande | Sublimering | ||
| Flytande | Frysning | Förångning | ||
| Gas | Deposition | Kondensation | Jonisering | |
| Plasma | Rekombination |
Se även
Anteckningar
- Anderson, John D. (1984). Aerodynamiks grunder . McGraw-Hill högre utbildning. ISBN 978-0-07-001656-9 .
- John, James (1984). Gasdynamik . Allyn och Bacon. ISBN 978-0-205-08014-4 .
- McPherson, William; Henderson, William (1917). En elementär studie av kemi .
Vidare läsning
- Philip Hill och Carl Peterson. Mechanics and Thermodynamics of Propulsion: Andra upplagan Addison-Wesley, 1992. ISBN 0-201-14659-2
- National Aeronautics and Space Administration (NASA). Animerat gaslabb . Öppnad februari 2008.
- Georgia State University. Hyperfysik . Öppnad februari 2008.
- Antony Lewis WordWeb . Öppnad februari 2008.
- Northwestern Michigan College The Gaseous State . Öppnad februari 2008.
- Lewes, Vivian Byam; Lunge, Georg (1911). . Encyclopædia Britannica . Vol. 11 (11:e upplagan). sid. 481–493.













