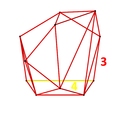
Runcinerade 24-celler

Ortogonala projektioner i F ₄ Coxeter-plan
24-celler	Runcinerad 24-celler
Runcitruncated 24-cell	Omnitruncated 24-cell (Runcicantruncated 24-cell)

I fyrdimensionell geometri är en runcinerad 24-cell en konvex enhetlig 4-polytop , som är en runcination (en 3:e ordningens trunkering) av den vanliga 24-cellen .

Det finns 3 unika grader av runcinationer av 24-cellen inklusive med permutationer trunkationer och kantelleringar.

Runcinerad 24-celler

Runcinerad 24-celler
Typ	Uniform 4-polytop
Schläfli symbol	t _0,3 {3,4,3}
Coxeter diagram
Celler	240	48 3.3.3.3 192 3.4.4
Ansikten	672	384{3} 288{4}
Kanter	576
Vertices	144
Vertex figur	långsträckt kvadratisk antiprisma
Symmetrigrupp	Aut (F ₄ ), [[3,4,3]], order 2304
Egenskaper	konvex , kanttransitiv
Enhetligt index	25 26 27

Netto

I geometri är den runcinerade 24-cells eller lilla prismatotetracontoctachoronen en enhetlig 4-polytop som begränsas av 48 oktaedrar och 192 triangulära prismor . De oktaedriska cellerna motsvarar cellerna i en 24-cell och dess dubbla.

EL Elte identifierade den 1912 som en halvregelbunden polytop.

Alternativa namn

Runcinerad 24-celler ( Norman W. Johnson )
Runcinerat icositetrachoron
Runcinerad polyoktaeder
Liten prismatotetracontoctachoron (spic) (Jonathan Bowers)

Koordinater

De kartesiska koordinaterna för den runcinerade 24-cellen med kantlängd 2 ges av alla permutationer av tecken och koordinater för:

(0, 0, √ 2 , 2+ √ 2 )

(1, 1, 1+ √ 2 , 1+ √ 2 )

Permutationerna för den andra uppsättningen koordinater sammanfaller med hörnen på en inskriven kantellerad tesserakt .

Projektioner

ortografiska projektioner
Coxeter plan	F ₄	B ₄
Graf
Dihedral symmetri	[[12]] = [24]	[8]
Coxeter plan	B ₃ / A ₂	B ₂ / A ₃
Graf
Dihedral symmetri	[6]	[[4]] = [8]

3D-perspektivprojektioner
Schlegel-diagram , centrerad på oktaeder, med oktaedrarna visade.	Perspektivprojektion av den runcinerade 24-cellen i 3 dimensioner, centrerad på en oktaedrisk cell. Rotationen är endast av 3D-bilden, för att visa dess struktur, inte en rotation i 4-rum. Femton av de oktaedriska cellerna som vetter mot 4D-vyn visas här i rött. Mellanrummen mellan dem fylls upp av ett ramverk av triangulära prismor.	Stereografisk projektion med 24 av dess 48 oktaedriska celler

Relaterad regelbunden sned polyeder

Den vanliga sneda polyedern , {4,8|3}, finns i 4-mellanrum med 8 kvadrater runt varje vertex, i en sicksackande icke-plan vertexfigur. Dessa fyrkantiga ytor kan ses på den runcinerade 24-cellen, med alla 576 kanter och 288 hörn. De 384 triangulära ytorna på den runcinerade 24-cellen kan ses som borttagna. Den dubbla regelbundna sneda polyedern, {8,4|3}, är på liknande sätt relaterad till de åttakantiga ytorna på den bitrunkerade 24-cellen .

Runcitruncated 24-cell

Runcitruncated 24-cell
Typ	Uniform 4-polytop
Schläfli symbol	t _0,1,3 {3,4,3} s _2,3 {3,4,3}
Coxeter diagram
Celler	240	24 4.6.6 96 4.4.6 96 3.4.4 24 3.4.4.4
Ansikten	1104	192{3} 720{4} 192{6}
Kanter	1440
Vertices	576
Vertex figur	Trapetsformad pyramid
Symmetrigrupp	F ₄ , [3,4,3], order 1152
Egenskaper	konvex
Enhetligt index	28 29 30

Netto

Det runcitruncerade 24-cells- eller prismatorhomberade icositetrachoronet är en enhetlig 4-polytop härledd från 24-cellen . Den avgränsas av 24 trunkerade oktaedrar , motsvarande cellerna i en 24-cells , 24 rhombicuboctaedra , motsvarande cellerna i de dubbla 24-cellerna, 96 triangulära prismor och 96 hexagonala prismor .

Koordinater

De kartesiska koordinaterna för en ursprungscentrerad runcitruncated 24-cell med kantlängd 2 ges av alla permutationer av koordinater och tecken på:

(0, √ 2 , 2 √ 2 , 2+3 √ 2 )

(1, 1+ √ 2 , 1+2 √ 2 , 1+3 √ 2 )

Permutationerna för den andra uppsättningen koordinater ger hörn av en inskriven omnitruncerad tesserakt .

Den dubbla konfigurationen har koordinater genererade från alla permutationer och tecken på:

(1,1,1+ √ 2 ,5+ √ 2 )

(1,3,3+ √ 2 ,3+ √ 2 )

(2,2,2+ √ 2 ,4+ √ 2 )

Projektioner

ortografiska projektioner
Coxeter plan	F ₄
Graf
Dihedral symmetri	[12]
Coxeter plan	B ₃ / A ₂ (a)	B ₃ / A ₂ (b)
Graf
Dihedral symmetri	[6]	[6]
Coxeter plan	B ₄	B ₂ / A ₃
Graf
Dihedral symmetri	[8]	[4]

Schlegel-diagram centrerat på rhombicuboctahedron endast triangulära prismor visas

Runcicantic snub 24-celler

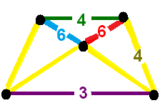
En halvsymmetrisk konstruktion av den runcicantellerade 24-cellen (eller runcicantellated 24-cellen), som också kallas en runcicantic snub 24-cell , som , har en identisk geometri, men dess triangulära ytor är ytterligare uppdelade. Liksom den snubbade 24-cellen har den symmetri [3 ⁺ ,4,3], ordning 576. Den runcitruncerade 24-cellen har 192 identiska hexagonala ytor, medan den runcicantic snub 24-cellen har 2 konstruktiva uppsättningar av 96 hexagoner. Skillnaden kan ses i vertexfigurerna :

Runcic snub 24-celler

Runcic snub 24-celler
Schläfli symbol	s ₃ {3,4,3}
Coxeter diagram
Celler	240	24 {3,5} 24 t{3,3} 96 (4.4.3) 96 tricup
Ansikten	960	576 {3} 288 {4} 96 {6}
Kanter	1008
Vertices	288
Vertex figur
Symmetrigrupp	[3 ⁺ ,4,3], order 576
Egenskaper	konvex

En besläktad 4-polytop är runcic snub 24-cell eller prismatorhombisnub icositetrachoron , s ₃ {3,4,3}, . Den är inte enhetlig, men den är vertextransitiv och har alla vanliga polygonytor. Den är konstruerad med 24 icosaedrar , 24 trunkerade tetraedrar , 96 triangulära prismor och 96 triangulära kupoler i mellanrummen, för totalt 240 celler, 960 ytor, 1008 kanter och 288 hörn. Liksom 24-cellssnubben har den symmetri [3 ⁺ ,4,3], ordning 576.

Hönsfiguren innehåller en ikosaeder, två triangulära prismor, en trunkerad tetraeder och 3 triangulära kupoler .

Ortografiska projektioner			Netto

Omnitruncerad 24-celler

Omnitruncerad 24-celler
Typ	Uniform 4-polytop
Schläfli symbol	t _0,1,2,3 {3,4,3}
Coxeter diagram
Celler	240	48 (4.6.8) 192 (4.4.6)
Ansikten	1392	864 {4} 384 {6} 144 {8}
Kanter	2304
Vertices	1152
Vertex figur	Fylisk disfenoid
Symmetrigrupp	Aut (F ₄ ), [[3,4,3]], order 2304
Egenskaper	konvex
Enhetligt index	29 30 31

Det omnitrunkerade 24-cells- eller stora prismatotetrakontoktakoronet är en enhetlig 4-polytop som härrör från 24-cellen . Den består av 1152 hörn, 2304 kanter och 1392 ytor (864 rutor, 384 hexagoner och 144 oktagoner). Den har 240 celler: 48 trunkerade cuboctahedra , 192 sexkantiga prismor . Varje vertex innehåller fyra celler i en phyllisk disfenoidal vertexfigur : två hexagonala prismor och två trunkerade cuboctaedra .

Strukturera

De 48 trunkerade kuboktaedriska cellerna är förenade med varandra via sina åttakantiga ytor. De kan grupperas i två grupper om 24 vardera, motsvarande cellerna i en 24-cell och dess dubbla. Mellanrummen mellan dem fylls i av ett nätverk av 192 hexagonala prismor, förenade med varandra via alternerande fyrkantiga ytor i alternerande orientering, och till de trunkerade cuboctaedrarna via deras hexagonala ytor och kvarvarande fyrkantiga ytor.

Koordinater

De kartesiska koordinaterna för en omnitruncerad 24-cell med kantlängd 2 är alla permutationer av koordinater och tecken på:

(1, 1+ √ 2 , 1+2 √ 2 , 5+3 √ 2 )

(1, 3+ √ 2 , 3+2 √ 2 , 3+3 √ 2 )

(2, 2+ √ 2 , 2+ 2 √ 2 , 4+3 √ 2 )

Bilder

ortografiska projektioner
Coxeter plan	F ₄	B ₄
Graf
Dihedral symmetri	[[12]] = [24]	[8]
Coxeter plan	B ₃ / A ₂	B ₂ / A ₃
Graf
Dihedral symmetri	[6]	[[4]] = [8]

3D-perspektivprojektioner
Schlegel diagram	Perspektivprojektion i 3D centrerad på en trunkerad kuboktaeder. Den närmaste stora rhombicuboctaedriska cellen till 4D-vyn visas i rött, med de sex omgivande stora rhombicuboctaedrarna i gult. Tolv av de hexagonala prismorna som delar en fyrkantig yta med närmaste cell och hexagonala ytor med de gula cellerna visas i blått. De återstående cellerna visas i grönt. Celler som ligger på andra sidan polytopen från 4D-synpunkt har utrangerats för tydlighetens skull.

Netto
Omnitruncerad 24-celler	Dubbla till omnitruncerade 24-celler

Besläktade polytoper

Olikformiga varianter med [3,4,3] symmetri och två typer av trunkerade kuboktaedrar kan fördubblas genom att placera de två typerna av trunkerade kuboktaedrar på varandra för att producera en olikformig polykoron med 48 trunkerade kuboktaedrar , 144 åttkantiga trapets ditezotragonprismor), 192 hexagonala prismor , två sorters 864 rektangulära trapetsprismor (288 med D _2d symmetri och 576 med C _2v symmetri) och 2304 hörn. Dess vertexfigur är en oregelbunden triangulär bipyramid .

Vertex figur

Denna polykoron kan sedan alterneras för att producera en annan olikformig polykoron med 48 snubkuber , 144 kvadratiska antiprismor , 192 oktaedrar (som triangulära antiprismor), tre typer av 2016 tetraedrar (288 tetragonala disfenoider, 576 fylliga disfenoider, 1152 och 576 phylliska disfenoider, 1152 och 1152 och 1152 hörn. Den har en symmetri på [[3,4,3] ⁺ ], ordning 1152.

Vertex figur

Full snubb 24-celler

Vertexfigur för omnisnub 24-cell

Den enhetliga snub 24-cellen kallas en semi-snub 24-cell av John Horton Conway med Coxeter-diagram inom F ₄ -familjen, även om det är en full snub eller omnisnub inom D ₄ -familjen, som .

Däremot kan en full snub 24-cell eller omnisnub 24-cell , definierad som en alternering av den omnitrunkerade 24-cellen, inte göras enhetlig, men den kan ges Coxeter-diagram och symmetri [[3,4,3]] ⁺ , order 1152, och konstruerad av 48 snubbar , 192 oktaedrar och 576 tetraedrar som fyller luckorna vid de borttagna hörnen. Dess vertexfigur innehåller 4 tetraedrar, 2 oktaedrar och 2 snubkuber. Den har 816 celler, 2832 ytor, 2592 kanter och 576 hörn.

Besläktade polytoper

Polytoper i 24-cellsfamiljen
namn	24-celler	trunkerad 24-cell	snubb 24-celler	likriktad 24-cell	kantellerad 24-cell	bitrunkerade 24-celler	cantitruncated 24-cell	runcinerad 24-celler	runcitruncated 24-cell	omnitruncerad 24-cell
Schläfli symbol	{3,4,3}	t _0,1 {3,4,3} t{3,4,3}	s{3,4,3}	t ₁ {3,4,3} r{3,4,3}	t _0,2 {3,4,3} rr{3,4,3}	t _1,2 {3,4,3} 2t{3,4,3}	t _0,1,2 {3,4,3} tr{3,4,3}	t _0,3 {3,4,3}	t _0,1,3 {3,4,3}	t _0,1,2,3 {3,4,3}
Coxeter diagram
Schlegel diagram
F ₄
B ₄
B ₃ (a)
B ₃ (b)
B ₂

Anteckningar

Kaleidoscopes: Selected Writings of HSM Coxeter , redigerad av F. Arthur Sherk, Peter McMullen, Anthony C. Thompson, Asia Ivic Weiss, Wiley-Interscience Publication, 1995, ISBN 978-0-471-01003-6
- (Papper 22) HSM Coxeter, Regular and Semi-Regular Polytopes I , [Math. Zeit. 46 (1940) 380-407, MR 2,10]
- (Papper 23) HSM Coxeter, Regular and Semi-Regular Polytopes II , [Math. Zeit. 188 (1985) 559-591]
- (Papper 24) HSM Coxeter, Regular and Semi-Regular Polytopes III , [Math. Zeit. 200 (1988) 3-45]
JH Conway och MJT Guy : Fyrdimensionella arkimediska polytoper , Proceedings of the Colloquium on Convexity at Copenhagen, sidan 38 och 39, 1965
NW Johnson : Theory of Uniform Polytopes and Honeycombs , Ph.D. Avhandling, University of Toronto, 1966
Fyrdimensionella arkimedeiska polytoper (tyska), Marco Möller, 2004 doktorsavhandling [1] m58 m59 m53
3. Konvex enhetlig polychora baserad på icositetrachoron (24-cell), George Olshevsky.
Klitzing, Richard. "4D enhetliga polytoper (polychora)" . x3o4o3x - spic, x3x4o3x - prico, s3s4o3x - prissi, x3x4x3x - gippic

Grundläggande konvexa regelbundna och enhetliga polytoper i dimensionerna 2–10
Familj	A _n	B _n	I ₂ (p) / D _n	E ₆ / E ₇ / E ₈ / F ₄ / G ₂	H _n
Vanlig polygon	Triangel	Fyrkant	p-gon	Sexhörning	Pentagon
Uniform polyeder	Tetraeder	Oktaeder • Kub	Demicube		Dodekaeder • Ikosaeder
Uniform polychoron	Pentachoron	16-celler • Tesseract	Demitesseract	24-celler	120-celler • 600-celler
Uniform 5-polytop	5-simplex	5-ortoplex • 5-kub	5-demikub
Uniform 6-polytop	6-simplex	6-ortoplex • 6-kub	6-demikub	1 ₂₂ • 2 ₂₁
Uniform 7-polytop	7-simplex	7-ortoplex • 7-kub	7-demikub	1 ₃₂ • 2 ₃₁ • 3 ₂₁
Uniform 8-polytop	8-simplex	8-ortoplex • 8-kub	8-demikub	1 ₄₂ • 2 ₄₁ • 4 ₂₁
Uniform 9-polytop	9-simplex	9-ortoplex • 9-kub	9-demikub
Uniform 10-polytop	10-simplex	10-ortoplex • 10-kub	10-demikub
Uniform n - polytop	n - simplex	n - ortoplex • n - kub	n - demikub	1 _k2 • 2 _k1 • k ₂₁	n - femkantig polytop
Ämnen: Polytopfamiljer • Vanlig polytop • Lista över vanliga polytoper och sammansättningar