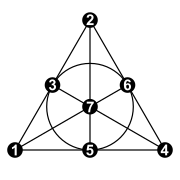
Fano plan

Fano-planet

Fano plan
Beställa	2
Lenz-Barlotti klass	VII.2
Automorfismer	$2^{3}\times 3\times 7$$PGL(3,2)$
Punkt omloppslängder	7
Linjens omloppslängder	7
Egenskaper	Desarguesian Self-dual

I finit geometri är Fano -planet (efter Gino Fano ) ett ändligt projektivt plan med minsta möjliga antal punkter och linjer: 7 punkter och 7 linjer, med 3 punkter på varje linje och 3 linjer genom varje punkt. Dessa punkter och linjer kan inte existera med detta mönster av incidenser i euklidisk geometri , men de kan ges koordinater genom att använda det finita fältet med två element. Standardnotationen för detta plan, som medlem av en familj av projektiva utrymmen , är PG(2, 2) . Här PG för " projektiv geometri ", den första parametern är den geometriska dimensionen (det är ett plan med dimension 2) och den andra parametern är ordningen (antal punkter per linje, minus en).

Fano-planet är ett exempel på en finit infallsstruktur , så många av dess egenskaper kan fastställas med hjälp av kombinatoriska tekniker och andra verktyg som används i studien av incidensgeometrier . Eftersom det är ett projektivt utrymme kan algebraiska tekniker också vara effektiva verktyg i dess studie.

Homogena koordinater

Fano-planet kan konstrueras via linjär algebra som det projektiva planet över det finita fältet med två element. Man kan på liknande sätt konstruera projektiva plan över vilket annat ändligt fält som helst, där Fano-planet är det minsta.

Genom att använda standardkonstruktionen av projektiva utrymmen via homogena koordinater , kan de sju punkterna i Fano-planet märkas med de sju icke-nollordnade trippelna av binära siffror 001, 010, 011, 100, 101, 110 och 111. Detta kan vara gjort på ett sådant sätt att för varannan punkt p och q har den tredje punkten på linjen pq etiketten bildad genom att lägga till beteckningarna p och q modulo 2. Med andra ord, punkterna i Fano-planet motsvarar icke- nollpunkter i det finita vektorutrymmet av dimension 3 över det finita fältet av ordning 2.

På grund av denna konstruktion anses Fano-planet vara ett Desarguesian-plan , även om planet är för litet för att innehålla en icke-degenererad Desargues-konfiguration (som kräver 10 punkter och 10 linjer).

Linjerna i Fano-planet kan också ges homogena koordinater, återigen med användning av trippel av binära siffror som inte är noll. Med detta koordinatsystem faller en punkt mot en linje om koordinaten för punkten och koordinaten för linjen har ett jämnt antal positioner där de båda har bitar som inte är noll: till exempel hör punkten 101 till linjen 111 , eftersom de har bitar som inte är noll vid två gemensamma positioner. När det gäller den underliggande linjära algebra, tillhör en punkt en linje om den inre produkten av vektorerna som representerar punkten och linjen är noll.

Linjerna kan delas in i tre typer.

• På tre av linjerna har de binära tripplarna för punkterna nollan i en konstant position: linjen 100 (som innehåller punkterna 001, 010 och 011) har 0 i den första positionen, och raderna 010 och 001 bildas i samma sätt.
• På tre av linjerna har två av positionerna i de binära trippelna av varje punkt samma värde: på raden 110 (som innehåller punkterna 001, 110 och 111) är den första och den andra positionen alltid lika, och linjerna 101 och 011 bildas på samma sätt.
• På den återstående raden 111 (innehållande punkterna 011, 101 och 110) har varje binär trippel exakt två bitar som inte är noll.

Gruppteoretisk konstruktion

Alternativt motsvarar planets 7 punkter de 7 icke-identitetselementen i gruppen ( Z ₂ ) ³ = Z ₂ × Z ₂ × Z ₂ . Linjerna i planet motsvarar undergrupperna av ordning 4, isomorfa till Z ₂ × Z ₂ . Automorfigruppen GL(3,2) i gruppen ( Z2 ) ³ är den för Fano-planet och har ordning 168 _.

Levi graf

Tvådelad Heawood-graf. Punkter representeras av hörn i en färg och linjer av hörn i den andra färgen.

Som med vilken infallsstruktur som helst, är Levi-grafen för Fano-planet en tvådelad graf , vars hörn representerar punkterna och den andra representerar linjerna, med två hörn sammanfogade om motsvarande punkt och linje är infallande . Denna speciella graf är en sammankopplad kubikgraf (regelbunden av grad 3), har omkrets 6 och varje del innehåller 7 hörn. Det är Heawood-grafen , den unika 6-buren .

Kollinationer

En kollinering av Fano-planet som motsvarar 3-bitars Gray- kodpermutation

En kollinering , automorfism eller symmetri av Fano-planet är en permutation av de 7 pekar som bevarar kollinearitet: det vill säga, det bär kolinjära punkter (på samma linje) till kolinjära punkter. Genom grundsatsen för projektiv geometri är den fullständiga kollineringsgruppen (eller automorfismgruppen , eller symmetrigruppen ) den projektiva linjära gruppen PGL(3,2), även betecknad $\mathrm {PGL } _{3}(\mathbb {F} _{2})$ . Eftersom fältet endast har ett element som inte är noll, är denna grupp isomorf till den projektiva speciella linjära gruppen PSL(3,2) och den allmänna linjära gruppen GL(3,2). Det är också isomorft till PSL(2,7).

Detta är en välkänd grupp av ordningen 168 = 2 ³ ·3·7, nästa icke-abelska enkla grupp efter A ₅ av ordningen 60 (ordnad efter storlek).

Som en permutationsgrupp som verkar på planets 7 punkter är kollineringsgruppen dubbelt transitiv , vilket betyder att vilket ordnat par av punkter som helst kan mappas av åtminstone en kollination till vilket annat ordnat punkter som helst. (Se nedan.)

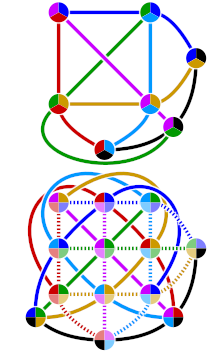
Kollinationer kan också ses som de färgbevarande automorfismerna i Heawood-grafen (se figur).

$\mathbb {F} _{8}$ är en förlängning av tre grader av ${\displaystyle \mathbb {F} _{2}} ,$ så punkterna i Fano-planet kan identifieras med $\mathbb {F} _{8}\setminus \{0\}$ . Symmetrigruppen kan skrivas $PGL(3,2)=Aut(\mathbb {P} ^{2}\mathbb {F} _{2})$ . På liknande sätt, $PSL(2,7)=Aut(\mathbb {P} ^{1}\mathbb {F} _{7} )$ . Det finns en relation mellan de underliggande objekten, $\mathbb {P} ^{2}\mathbb {F} _{2}$ och $\mathbb {P} ^{ 1}\mathbb {F} _{7}$ kallas Kattens vagga-karta. Färglägg de sju linjerna på Fano-planet ROYGBIV, placera fingrarna i det tvådimensionella projektiva utrymmet i omgivande 3-utrymme och sträck ut fingrarna som barnspelet Cat's Cradle. Du får en komplett graf på sju hörn med sju färgade trianglar (projektiva linjer). Det saknade ursprunget för $\mathbb {F} _{8}$ kommer att vara i mitten av septagonen inuti. Märk nu denna punkt som $\infty$ , och dra den bakåt till origo. Man kan skriva ner en bijektion från $\mathbb {F} _{7}\cup \{\infty \}$ till $\mathbb {F} _{8}$ . Ställ in $x^{\infty }=0$ och skicka lutningen $k\ mapsto x^{\infty }+x^{k}\in \mathbb {F} _{8}\cong \mathbb {F} _{2}[x]/(x^{3}+x+1)$ där nu $x^{k}$ betecknar hörnen av $K_{7}$ med kantfärgning , och noterar att $\mathbb {F} _{8}^ {*}$ är en cyklisk grupp av ordning 7. Symmetrierna för $\mathbb {P} ^{1}\mathbb {F} _{7}$ är Möbiustransformationer , och de grundläggande transformationerna är reflektioner (ordning 2, $k\mapsto -1/k$ ), översättningar (ordning 7, ${\displaystyle k\mapsto k+1} )$ och dubblering (ordning 3 eftersom $2^{3}=1$ , $k\mapsto 2k$ ). Motsvarande symmetrier på Fano-planet är att byta hörn, rotera grafen och rotera trianglar.

Bijektion mellan Fano-planet som fält med åtta element minus origo och den projektiva linjen över fältet med sju element. Symmetrier görs tydliga.

Dualitet i Fano-planet: Varje punkt motsvarar en linje och vice versa.

Dualiteter

Huvudartikel: Dualitet (projektiv geometri)

En bijektion mellan punktmängden och linjemängden som bevarar incidensen kallas en dualitet och en dualitet av ordning två kallas polaritet .

Dualiteter kan ses i samband med Heawood-grafen som färgreverserande automorfismer. Ett exempel på en polaritet ges genom reflektion genom en vertikal linje som halverar Heawood-grafrepresentationen som ges till höger. Förekomsten av denna polaritet visar att Fano-planet är självdubbelt . Detta är också en omedelbar konsekvens av symmetrin mellan punkter och linjer i definitionen av incidensrelationen i termer av homogena koordinater, som beskrivs i ett tidigare avsnitt.

Cykelstruktur

En siffra numrering av Fano-planet

Permutationsgruppen med 7 poäng har 6 konjugationsklasser .

Dessa fyra cykelstrukturer definierar var och en en enda konjugationsklass:

• Identitetsförändringen
• 21 permutationer med två 2-cykler
• 42 permutationer med en 4-cykel och en 2-cykel
• 56 permutationer med två 3-cykler

De 48 permutationerna med en komplett 7-cykel bildar två distinkta konjugationsklasser med 24 element:

• A mappar till B , B till C , C till D. Då är D på samma linje som A och B .
• A mappar till B , B till C , C till D. Då är D på samma linje som A och C .

(Se här för en komplett lista.)

Därav , enligt Pólyas uppräkningssats , är antalet olikvärdiga färger i Fano-planet med n färger ${{n^{7}+21n^{5 }+98n^{3}+48n} \over 168}$ (sekvens A241929 i OEIS ).

Kompletta quadrangles och Fano underplan

Huvudartikel: Komplett fyrkant

I något projektivt plan är en uppsättning av fyra punkter, varav inte tre är kolinjära, och de sex linjerna som förenar paren av dessa punkter är en konfiguration som kallas en komplett fyrkant . Linjerna kallas sidor och par av sidor som inte möts i någon av de fyra punkterna kallas motstående sidor . Punkterna där motsatta sidor möts kallas diagonala punkter och det finns tre av dem.

Om denna konfiguration ligger i ett projektivt plan och de tre diagonala punkterna är kolinjära, bildar de sju punkterna och sju linjerna i den expanderade konfigurationen ett underplan av det projektiva planet som är isomorft till Fano-planet och kallas ett Fano- underplan .

Ett berömt resultat, på grund av Andrew M. Gleason säger att om varje komplett fyrkant i ett ändligt projektivt plan sträcker sig till ett Fano-underplan (det vill säga har kolinjära diagonala punkter) så är planet Desarguesian. Gleason kallade vilket projektivt plan som helst som uppfyller detta villkor för ett Fano-plan vilket skapade en viss förvirring med modern terminologi. För att förvärra förvirringen Fanos axiom att diagonalpunkterna i en komplett fyrkant aldrig är kolinjära, ett tillstånd som gäller i det euklidiska och verkliga projektiva planet. Det Gleason kallade Fano-planen uppfyller alltså inte Fanos axiom.

Konfigurationer

Fano-planet innehåller följande antal konfigurationer av punkter och linjer av olika typer. För varje typ av konfiguration är antalet kopior av konfiguration multiplicerat med antalet symmetrier i planet som håller konfigurationen oförändrad lika med 168, storleken på hela kollineringsgruppen, förutsatt att varje kopia kan mappas till vilken annan kopia som helst ( se Orbit-Stabiliser-satsen ). Eftersom Fano-planet är självdubbelt kommer dessa konfigurationer i dubbla par och det kan visas att antalet kollinationer som fixerar en konfiguration är lika med antalet kollinationer som fixar dess dubbla konfiguration.

• Det finns 7 punkter med 24 symmetrier som fixerar vilken punkt som helst och dubbelt så finns det 7 linjer med 24 symmetrier som fixerar vilken linje som helst. Antalet symmetrier följer av kollineationsgruppens 2-transitivitet, vilket innebär att gruppen agerar transitivt på punkterna.
• Det finns 42 ordnade par av punkter, och var och en kan mappas med en symmetri på vilket annat ordnat par som helst. För alla beställda par finns det 4 symmetrier som fixerar det. På motsvarande sätt finns det 21 oordnade par av punkter, som var och en kan mappas med en symmetri på vilket annat oordnat par som helst. För alla oordnade par finns det 8 symmetrier som fixerar det.
• Det finns 21 flaggor som består av en linje och en punkt på den linjen. Varje flagga motsvarar det oordnade paret av de andra två punkterna på samma linje. För varje flagga håller 8 olika symmetrier den fast.
• Det finns 7 sätt att välja en fyrkant med fyra (oordnade) punkter, varav tre är kolinjära. Dessa fyra punkter utgör komplementet till en linje, som är den diagonala linjen i fyrkanten och en kollinering fixerar fyrkanten om och bara om den fixerar den diagonala linjen. Det finns alltså 24 symmetrier som fixerar en sådan fyrkant. Den dubbla konfigurationen är en fyrhörning som består av fyra linjer varav tre möts vid en punkt och deras sex skärningspunkter, det är komplementet till en punkt i Fano-planet.
• Det finns ${\tbinom {7}{3}}=35$ tripplar av punkter, varav sju är kolinjära tripplar, vilket lämnar 28 icke-kollinjära tripplar eller trianglar . Konfigurationen som består av de tre punkterna i en triangel och de tre linjerna som förenar paren av dessa punkter representeras av en 6-cykel i Heawood-grafen. En färgbevarande automorfism av Heawood-grafen som fixerar varje vertex i en 6-cykel måste vara identitetsautomorfismen. Detta betyder att det finns 168 märkta trianglar fixerade endast av identitetskollineringen och endast sex kollinationer som stabiliserar en omärkt triangel, en för varje permutation av punkterna. Dessa 28 trianglar kan ses som motsvarande de 28 bitangenterna i en kvarts . Det finns 84 sätt att specificera en triangel tillsammans med en särskiljande punkt på den triangeln och två symmetrier som fixerar denna konfiguration. Dual av triangelkonfigurationen är också en triangel.
• Det finns 28 sätt att välja en punkt och en linje som inte faller mot varandra (en anti-flagga ), och sex sätt att permutera Fano-planet samtidigt som en anti-flagga fixeras. För varje icke-infallande punktlinjepar ( p , l ), ​​bildar de tre punkter som är olikvärdiga med p och som inte hör till l en triangel, och för varje triangel finns det ett unikt sätt att gruppera de återstående fyra punkterna i en anti-flagga.
• Det finns 28 sätt att specificera en hexagon där inga tre på varandra följande hörn ligger på en linje, och sex symmetrier som fixerar en sådan hexagon.
• Det finns 84 sätt att specificera en femhörning där inga tre på varandra följande hörn ligger på en linje, och två symmetrier som fixerar någon femhörning.

Fano-planet är ett exempel på en ( n ₃ ) -konfiguration, det vill säga en uppsättning av n punkter och n linjer med tre punkter på varje linje och tre linjer genom varje punkt. Fano-planet, en (7 ₃ )-konfiguration, är unik och är den minsta sådana konfigurationen. Enligt en sats av Steinitz kan konfigurationer av denna typ realiseras i det euklidiska planet som har högst en krökt linje (alla andra linjer ligger på euklidiska linjer).

Den övre figuren är en alternativ representation av Fano-planet i rutnätslayout – jämför med ett av de finita projektiva planen av ordning 3 nedan

Blockdesignteori

Fano-planet är en liten symmetrisk blockdesign , närmare bestämt en 2-(7,3,1)-design. Designens punkter är planets punkter, och designens block är planets linjer. Som sådan är det ett värdefullt exempel inom (block)designteori.

₀ Med punkterna märkta 0, 1, 2, ..., 6 är linjerna (som punktmängder) översättningarna av den (7, 3, 1) plana skillnadsmängden som ges av {0, 1, 3} i gruppen $Z} /7\mathbb {Z} .}$ { Med linjerna märkta ℓ , ..., ℓ ₆ ges incidensmatrisen (tabell) av :

Punkt Linje	0	1	2	3	4	5	6
ℓ0	1	1	0	1	0	0	0
ℓ 1	0	1	1	0	1	0	0
ℓ 2	0	0	1	1	0	1	0
ℓ 3	0	0	0	1	1	0	1
ℓ 4	1	0	0	0	1	1	0
ℓ 5	0	1	0	0	0	1	1
ℓ 6	1	0	1	0	0	0	1

Steiner-systemet

Huvudartikel: Steiner-systemet

Fano-planet, som blockdesign, är ett Steiner-trippelsystem . Som sådan kan den ges strukturen av en kvasigrupp . Denna kvasigrupp sammanfaller med den multiplikativa strukturen som definieras av enheten oktonioner e ₁ , e ₂ , ..., e ₇ (utelämnar 1) om tecknen på oktonionprodukterna ignoreras ( Baez 2002 ).

Matroid teori

Huvudartikel: Matroidteori

Fano-matroiden $F_{7}$ bildas genom att ta Fano-planets punkter som markmängd, och de icke-kollinjära delmängderna med tre element som baser.

Fano-planet är ett av de viktiga exemplen i strukturteorin för matroider . Att utesluta Fano-planet som ett matroid-minor är nödvändigt för att karakterisera flera viktiga klasser av matroider, såsom vanliga , grafiska och kografiska.

Om du delar isär en linje i tre 2-punktslinjer får du "icke-Fano-konfigurationen", som kan bäddas in i det verkliga planet. Det är ett annat viktigt exempel inom matroidteorin, eftersom det måste uteslutas för att många satser ska hålla.

Fano-planet ritas om som en plan graf

PG(3,2)

Huvudartikel: PG(3,2)

Fano-planet kan förlängas i en tredje dimension för att bilda ett tredimensionellt projektivt utrymme, betecknat med PG(3,2) . Den har 15 punkter, 35 linjer och 15 plan och är det minsta tredimensionella projektiva utrymmet . Den har även följande egenskaper:

• Varje punkt finns i 7 linjer och 7 plan
• Varje linje finns i 3 plan och innehåller 3 punkter
• Varje plan innehåller 7 punkter och 7 linjer
• Varje plan är isomorft till Fano-planet
• Varje par av distinkta plan skär varandra i en linje
• En linje och ett plan som inte innehåller linjen skär varandra i exakt en punkt

Se även

• Projektiv konfiguration
• Transsylvaniens lotteri

Anteckningar

• Baez, John (2002), "The Octonions" , Bull. Amer. Matematik. Soc. , 39 (2): 145–205, arXiv : math/0105155 , doi : 10.1090/S0273-0979-01-00934-X ( Online HTML-version )
•    Dembowski, Peter (1968), Finite geometries , Ergebnisse der Mathematik und ihrer Grenzgebiete , Band 44, Berlin, New York: Springer-Verlag , ISBN 3-540-61786-8 , MR 0233275
•   Hirschfeld, JWP (1979), Projective Geometries Over Finite Fields , Oxford University Press , ISBN 978-0-19-850295-1
•   " Configurations of lines and models of Lie algebras", Journal of Algebra , 304 (1): 457–486, arXiv : math/0507118 , doi : 10.1016/j.jalgebra.2006.04.029 ISSN 0021-8693
•   Pisanski, Tomaž ; Servatius, Brigitte (2013), Konfigurationer ur en grafisk synvinkel , Birkhäuser, ISBN 978-0-8176-8363-4
•   Polster, Burkard (1998), A Geometrical Picture Book , Springer, ISBN 978-0-387-98437-7
•   van Lint, JH; Wilson, RM (1992), A Course in Combinatorics , Cambridge University Press, ISBN 978-0-521-42260-4

externa länkar

• Weisstein, Eric W. "Fano Plane" . MathWorld .