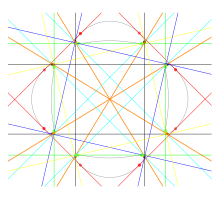
Bitangenter av en kvarts

Trottkurvan och sju av dess bitangenter. De andra är symmetriska med avseende på 90° rotationer genom origo.

Trott-kurvan med alla 28 bitangenter.

I teorin om algebraiska plankurvor har en allmän kvartsplanskurva 28 bitangenta linjer, linjer som tangerar kurvan på två ställen. Dessa linjer finns i det komplexa projektiva planet , men det är möjligt att definiera kvartskurvor för vilka alla dessa 28 linjer har reella tal som sina koordinater och därför tillhör det euklidiska planet .

En explicit kvarts med tjugoåtta reella bitangenter gavs först av Plücker ( 1839 ) Som Plücker visade måste antalet verkliga bitangenter i varje kvarts vara 28, 16 eller ett tal mindre än 9. En annan kvarts med 28 reella bitangenter kan vara bildas av platsen för centrum av ellipser med fasta axellängder, tangent till två icke-parallella linjer. Shioda (1995) gav en annan konstruktion av en kvarts med tjugoåtta bitangenter, bildad genom att utskjuta en kubisk yta ; tjugosju av bitangenterna till Shiodas kurva är verkliga medan den tjugoåttonde är linjen i oändligheten i det projektiva planet.

Exempel

Trott- kurvan , en annan kurva med 28 reella bitangenter, är den uppsättning punkter ( x , y ) som uppfyller polynomekvationen för grad fyra

$\displaystyle 144(x^{4}+y^{4})-225( x^{2}+y^{2})+350x^{2}y^{2}+81=0.$

Dessa punkter bildar en icke-singular kvartskurva som har släkte tre och som har tjugoåtta riktiga bitangenter .

Liksom exemplen på Plücker och Blum och Guinand har Trott-kurvan fyra separerade ovaler, det maximala antalet för en kurva av grad fyra, och är därmed en M-kurva . De fyra ovalerna kan grupperas i sex olika par av ovaler; för varje par ovaler finns det fyra bitangenter som rör båda ovalarna i paret, två som skiljer de två ovalarna åt och två som inte gör det. Dessutom avgränsar varje oval ett icke-konvext område av planet och har en bitangens som spänner över den icke-konvexa delen av dess gräns.

Anslutningar till andra strukturer

Den dubbla kurvan till en kvartskurva har 28 riktiga vanliga dubbelpunkter, dubbla till de 28 bitangenterna i den ursprungliga kurvan.

De 28 bitangenterna i en kvarts kan också placeras i överensstämmelse med formens symboler

${\begin{bmatrix}a&b&c\\d&e&f\\\end{bmatrix}}$

där a, b, c, d, e, f alla är noll eller ett och var

$ad+be+cf=1\ (\operatörsnamn {mod} \ 2).$

Det finns 64 val för a, b, c, d, e, f , men endast 28 av dessa val ger en udda summa. Man kan också tolka a, b, c som de homogena koordinaterna för en punkt i Fano-planet och d, e, f som koordinaterna för en linje i samma ändliga projektiva plan; villkoret att summan är udda motsvarar kravet att punkten och linjen inte berör varandra, och det finns 28 olika par av en punkt och en linje som inte berör varandra.

Punkterna och linjerna i Fano-planet som är åtskilda från ett icke-infallande punktlinjepar bildar en triangel, och bitangenterna i en kvarts har ansetts stämma överens med Fano-planets 28 trianglar. Levi -grafen för Fano-planet är Heawood-grafen , där trianglarna i Fano-planet representeras av 6-cykler. De 28 6-cyklerna i Heawood-grafen motsvarar i sin tur de 28 hörnen i Coxeter-grafen .

De 28 bitangenterna i en kvarts motsvarar också paren av de 56 linjerna på en grad-2 del Pezzo-yta och de 28 udda theta-egenskaperna .

De 27 linjerna på kuben och de 28 bitangenterna på en kvarts, tillsammans med de 120 tritangenta planen i en kanonisk sextisk kurva av släkte 4, bildar en " treenighet " i betydelsen Vladimir Arnold , närmare bestämt en form av McKay-korrespondens , och kan vara relaterad till många ytterligare föremål, inklusive E ₇ och E ₈ , som diskuterats vid treenighetstider .

Anteckningar

• Blum, R.; Guinand, AP (1964). "En quartic med 28 riktiga bitangenter" . Kanadensisk matematisk bulletin . 7 (3): 399–404. doi : 10.4153/cmb-1964-038-6 .
• Cayley, Arthur (1879), "On the bitangents of a quartic", Salmon's Higher Plane Curves , s. 387–389 . I The collected matematical papers of Arthur Cayley , Andrew Russell Forsyth, red., The University Press, 1896, vol. 11, s. 221–223.
•    Gray, Jeremy (1982), "From the history of a simple group", The Mathematical Intelligencer , 4 (2): 59–67, doi : 10.1007/BF03023483 , MR 0672918 , S2CID 14602496 . Omtryckt i    Levy, Silvio, red. (1999), The Eightfold Way , MSRI Publications, vol. 35, Cambridge University Press, s. 115–131, ISBN 0-521-66066-1 , MR 1722415 .
•   Manivel, L. (2006), "Configurations of lines and models of Lie algebras", Journal of Algebra , 304 (1): 457–486, arXiv : math/0507118 , doi : 10.1016 /j.jalgebra.2006.04.029 S2CID 17374533 .
• McKay, John; Sebbar, Abdellah (2007). "Replikerbara funktioner: en introduktion". Gränser i talteori, fysik och geometri II : 373–386. doi : 10.1007/978-3-540-30308-4_10 .
• Plücker, J. (1839), Theorie der algebraischen Curven: gegrundet auf eine neue Behandlungsweise der analytischen Geometrie , Berlin: Adolph Marcus .
• Riemann, GFB (1876), "Zur Theorie der Abel'schen Funktionen für den Fall p = 3", Ges. Werke , Leipzig, s. 456–472 . Som citeras av Cayley.
•   Shioda, Tetsuji (1995), "Weierstrass-transformationer och kubiska ytor" (PDF) , Commentarii Mathematici Universitatis Sancti Pauli , 44 (1): 109–128, MR 1336422
• Trott, Michael (1997), "Applying GroebnerBasis to Three Problems in Geometry", Mathematica in Education and Research , 6 (1): 15–28 .