Pólya uppräkningssats

Pólya -uppräkningssatsen , även känd som Redfield–Pólya-satsen och Pólya-räkning , är en sats inom kombinatorik som både följer av och i slutändan generaliserar Burnsides lemma om antalet banor för en grupphandling på en uppsättning . Satsen publicerades först av J. Howard Redfield 1927. År 1937 återupptäcktes den självständigt av George Pólya , som sedan kraftigt populariserade resultatet genom att tillämpa det på många räkneproblem, i synnerhet på uppräkningen av kemiska föreningar .

Pólya uppräkningssatsen har införlivats i symbolisk kombinatorik och teorin om kombinatoriska arter .

Förenklad, oviktad version

Låt X vara en finit mängd och låt G vara en grupp av permutationer av X (eller en finit symmetrigrupp som verkar på X ). Uppsättningen X kan representera en ändlig uppsättning av pärlor, och G kan vara en vald grupp av permutationer av pärlorna. Till exempel, om X är ett halsband med n pärlor i en cirkel, är rotationssymmetri relevant så G är den cykliska gruppen C _n , medan om X är ett armband med n pärlor i en cirkel är rotationer och reflektioner relevanta så G är den dihedriska gruppen D _n av ordningen 2 n . Antag vidare att Y är en ändlig uppsättning färger — kulornas färger — så att Y ^X är uppsättningen av färgade arrangemang av pärlor (mer formellt: Y ^X är uppsättningen funktioner ${\displaystyle X\to Y } .) Sedan$ agerar gruppen G på Y ^X . Pólya uppräkningssatsen räknar antalet banor under G för färgade arrangemang av pärlor med följande formel:

\left|Y^{X}/G\right|={\frac {1}{|G|}}\summa _{g\in G}m^{ c(g)}

där $m=|Y|$ är antalet färger och c ( g ) är antalet cykler för gruppelementet g när det betraktas som en permutation av X .

Full, viktad version

I den mer generella och viktigare versionen av satsen är färgerna också viktade på ett eller flera sätt, och det skulle kunna finnas ett oändligt antal färger förutsatt att färguppsättningen har en genererande funktion med ändliga koefficienter . I det univariata fallet, anta det

f(t)=f_{0}+f_{1}t+f_{2}t^{2}+\cdots

är den genererande funktionen för uppsättningen färger, så att det finns f _w färger med vikt w för varje heltal w ≥ 0. I det multivariata fallet är vikten av varje färg en vektor av heltal och det finns en genererande funktion f ( t ₁ , t ₂ , ...) som tabellerar antalet färger med varje given vektor av vikter.

Uppräkningssatsen använder en annan multivariat genererande funktion som kallas cykelindex :

Z_{G}(t_{1},t_{2},\ldots ,t_{n })={\frac {1}{|G|}}\summa _{g\in G}t_{1}^{c_{1}(g)}t_{2}^{c_{2}(g )}\cdots t_{n}^{c_{n}(g)}

där n är antalet element av X och c _k ( g ) är antalet k -cykler av gruppelementet g som en permutation av X .

Ett färgat arrangemang är en bana av verkan av G på mängden Y ^X (där Y är mängden färger och Y ^X anger mängden av alla funktioner φ: X → Y ). Vikten av ett sådant arrangemang definieras som summan av vikterna av φ( x ) över alla x i X . Satsen säger att genereringsfunktionen F för antalet färgade arrangemang efter vikt ges av:

F(t)=Z_{G}(f(t) ,f(t^{2}),f(t^{3}),\ldots ,f(t^{n}))

eller i det multivariata fallet:

F(t_{1},t_{2},\ldots )=Z_{G}(f(t_{1},t_{2},\ldots ),f(t_{1}^{2} ,t_{2}^{2},\ldots ),f(t_{1}^{3},t_{2}^{3},\ldots ),\ldots ,f(t_{1}^{n },t_{2}^{n},\ldots )).

För att reducera till den förenklade versionen som gavs tidigare, om det finns m färger och alla har vikten 0, då f ( t ) = m och

\left|Y^{X}/G\right|=F(0)=Z_{G}(m,m,\ldots ,m)={\frac {1}{|G|}}\ summa _{g\in G}m^{c(g)}.

I den berömda tillämpningen av att räkna träd (se nedan) och acykliska molekyler, är ett arrangemang av "färgade pärlor" faktiskt ett arrangemang av arrangemang, såsom grenar av ett rotat träd. Sålunda härleds den genererande funktionen f för färgerna från den genererande funktionen F för arrangemang, och Pólya-uppräkningssatsen blir en rekursiv formel.

Exempel

Halsband och armband

Färgade kuber

Hur många sätt finns det att färga sidorna av en tredimensionell kub med m färger, upp till rotation av kuben? Rotationsgruppen C i kuben verkar på de sex sidorna av kuben, vilket motsvarar pärlor. Dess cykelindex är

{\ displaystyle Z_{C}(t_{1},t_{2},t_{3},t_{4})={\frac {1}{24}}\left(t_{1}^{6}+6t_ {1}^{2}t_{4}+3t_{1}^{2}t_{2}^{2}+8t_{3}^{2}+6t_{2}^{3}\right)}

som erhålls genom att analysera verkan av vart och ett av de 24 elementen i C på de 6 sidorna av kuben, se här för detaljer.

Vi tar alla färger för att ha vikt 0 och finner att det finns

F(0)=Z_{C}(m,m ,m,m)={\frac {1}{24}}\left(m^{6}+3m^{4}+12m^{3}+8m^{2}\right)

olika färger.

Grafer på tre och fyra hörn

En graf på m hörn kan tolkas som ett arrangemang av färgade pärlor. Uppsättningen X av "pärlor" är uppsättningen av ${\binom {m}{2}}$ möjliga kanter, medan uppsättningen färger Y = {svart, vit} motsvarar kanter som finns närvarande (svart) eller frånvarande (vit). Pólya-uppräkningssatsen kan användas för att beräkna antalet grafer upp till isomorfism med ett fast antal hörn, eller genereringsfunktionen för dessa grafer enligt antalet kanter de har. För det senare syftet kan vi säga att en svart eller närvarande kant har vikten 1, medan en frånvarande eller vit kant har vikten 0. Således är ${\displaystyle f(t)=1+t$ } genereringsfunktionen för uppsättningen färger. Den relevanta symmetrigruppen är $G=S_{m},$ den symmetriska gruppen på m bokstäver. Denna grupp verkar på mängden X av möjliga kanter: en permutation φ förvandlar kanten {a, b} till kanten {φ(a), φ(b)}. Med dessa definitioner är en isomorfismklass av grafer med m hörn detsamma som en bana av verkan av G på mängden Y ^X av färgade arrangemang; antalet kanter på grafen är lika med vikten av arrangemanget.

Alla grafer på tre hörn

Nonisomorfa grafer på tre hörn

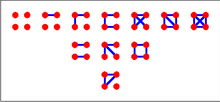
De åtta graferna på tre hörn (innan man identifierar isomorfa grafer) visas till höger. Det finns fyra isomorfismklasser av grafer, som också visas till höger.

Cykelindexet för gruppen _S3 som verkar på uppsättningen av tre kanter är

Z_{G}(t_{1},t_{2},t_{ 3})={\frac {1}{6}}\left(t_{1}^{3}+3t_{1}t_{2}+2t_{3}\right)

(erhålls genom att inspektera cykelstrukturen för gruppelementens verkan; se här ). Enligt uppräkningssatsen är alltså den genererande funktionen för grafer på 3 hörn upp till isomorfism

F(t)=Z_{G}\left(t+1,t^{2}+1,t^{3}+1\right)={\frac {1}{ 6}}\left((t+1)^{3}+3(t+1)(t^{2}+1)+2(t^{3}+1)\höger),

vilket förenklar till

F(t)=t^{3}+t^{2}+t+1.

Det finns alltså en graf vardera med 0 till 3 kanter.

Isomorfism klasser av grafer på fyra hörn.

Cykelindexet för gruppen _S4 som verkar på uppsättningen av 6 kanter är

Z_{G}( t_{1},t_{2},t_{3},t_{4})={\frac {1}{24}}\left(t_{1}^{6}+9t_{1}^{2 }t_{2}^{2}+8t_{3}^{2}+6t_{2}t_{4}\right)

(se här .) Därav

F(t)=Z_{G}\left(t+1,t^{2}+1, t^{3}+1,t^{4}+1\right)={\frac {(t+1)^{6}+9(t+1)^{2}(t^{2}+ 1)^{2}+8(t^{3}+1)^{2}+6(t^{2}+1)(t^{4}+1)}{24}}

vilket förenklar till

F(t)=t^{6}+t^{5}+2t^{ 4}+3t^{3}+2t^{2}+t+1.

Dessa grafer visas till höger.

Rotade ternära träd

Uppsättningen T ₃ av rotade ternära träd består av rotade träd där varje nod (eller icke-bladspunkt) har exakt tre barn (löv eller underträd). Små ternära träd visas till höger. Observera att rotade ternära träd med n noder är ekvivalenta med rotade träd med n toppar av högst 3 (genom att ignorera bladen). I allmänhet är två rotade träd isomorfa när det ena kan erhållas från det andra genom att permutera barnen i dess noder. Med andra ord, gruppen som verkar på barnen i en nod är den symmetriska gruppen S ₃ . Vi definierar vikten av ett sådant ternärt träd som antalet noder (eller icke-bladiga hörn).

Rotade ternära träd på 0, 1, 2, 3 och 4 noder (=icke-bladiga hörn). Roten visas i blått, bladen visas inte. Varje nod har så många löv som att antalet barn blir lika med 3.

Man kan se ett rotat tremärt träd som ett rekursivt objekt som antingen är ett löv eller en nod med tre barn som själva är rotade tremära träd. Dessa barn är likvärdiga med pärlor; cykelindexet för den symmetriska gruppen S3 som _verkar på dem är

Z_{S_{3}}(t_{1},t_{2},t_{3})={\frac {t_{1}^{3}+3t_{1}t_{2}+2t_ {3}}{6}}.

Polya-uppräkningssatsen översätter den rekursiva strukturen hos rotade ternära träd till en funktionell ekvation för genereringsfunktionen F(t) för rotade ternära träd efter antal noder. Detta uppnås genom att "färga" de tre barnen med rotade ternära träd, viktade med nodnummer, så att den färggenererande funktionen ges av $f(t)=F(t)$ som genom uppräkningssatsen ger

{\frac {F(t)^{3}+3F(t)F(t^{2 })+2F(t^{3})}{6}}

som genereringsfunktion för rotade ternära träd, viktade med en mindre än nodnumret (eftersom summan av barnvikterna inte tar hänsyn till roten), så att

F(t)=1+t\cdot {\frac {F(t)^{3}+3F(t)F(t^{2})+2F(t^{3})}{6 }}.

Detta motsvarar följande återkommande formel för antalet t _n av rotade ternära träd med n noder:

{\ displaystyle {\begin{aligned}t_{0}&=1\\t_{n+1}&={\frac {1}{6}}\left(\sum _{a+b+c=n}t_ {a}t_{b}t_{c}+3\summa _{a+2b=n}t_{a}t_{b}+2\summa _{3a=n}t_{a}\right)\end {Justerat}}}

där a , b och c är icke-negativa heltal.

De första värdena för $t_{n}$ är

1, 1, 1, 2, 4, 8, 17, 39, 89, 211, 507, 1238, 3057, 7639, 19241 (sekvens A000598 i OEIS )

Bevis för teorem

Den förenklade formen av Pólya-uppräkningssatsen följer av Burnsides lemma , som säger att antalet färgbanor är medeltalet av antalet element i $Y^{X}$ fixerat av permutationen g av G över alla permutationer g . Den viktade versionen av satsen har i huvudsak samma bevis, men med en förfinad form av Burnsides lemma för viktad uppräkning. Det motsvarar att applicera Burnsides lemma separat på banor med olika vikt.

För tydligare notation, låt $x_{1},x_{2},\ldots$ vara variablerna för den genererande funktionen f av $Y$ . Givet en vektor av vikter $\omega$ , låt $x^{\omega }$ beteckna motsvarande monomial term för f . Om man tillämpar Burnsides lemma på viktbanor $\omega$ , är antalet banor med denna vikt

{\frac {1}{|G|}}\sum _{g\in G}\left|(Y^{X})_{\omega ,g}\right|

där $(Y^{X})_{\omega ,g}$ är uppsättningen färger av vikt $\omega$ som också är fixerade med g . Om vi sedan summerar alla möjliga vikter får vi

F(x_{1},x_{2},\ldots )={\frac {1}{|G|}}\summa _{g\in G,\omega }x^{\omega }\ vänster|(Y^{X})_{\omega ,g}\right|.

Under tiden ett gruppelement g med cykelstruktur $j_{1}(g),j_{2}(g),\ldots ,j_ {n}(g)$ kommer att bidra med termen

t_{1}^{j_{1}(g)}t_{2}^{j_{2}( g)}\cdots t_{n}^{j_{n}(g)}

till cykelindexet för G . Elementet g fixerar ett element $\phi \in Y^{X}$ om och endast om funktionen φ är konstant på varje cykel q av g . För varje sådan cykel q, genererar funktionen i vikt av | q | identiska färger från uppsättningen som räknas upp av f är