Delat-komplext tal

"Dubbelt nummer" omdirigerar hit. För datornummerformat, se flyttalformat med dubbel precision .

I algebra är ett delat komplext tal (eller hyperboliskt tal , även perplextal , dubbeltal ) baserat på en hyperbolisk enhet j som uppfyller $j^{2}=1.$ Ett delat-komplext tal har två reella talkomponenter x och y , och skrivs $\displaystyle z=x+yj.}$ { Konjugatet av z är $z^{*}=x-yj.$ Eftersom ${\displaystyle j^{2}=1,} är$ produkten av ett tal z med dess konjugat ${\displaystyle N(z):=zz^{*}=x^{2}-y^{2},} en$ isotropisk kvadratisk form .

Samlingen D av alla delade komplexa tal $z=x+yj$ för $x,y\in \mathbb {R}$ bildar en algebra över fältet för reella tal . Två delade komplexa tal $N(wz)=N(w)N(z).$ och z har en produkt wz som uppfyller Denna sammansättning av N över algebraprodukten gör ( D , +, ×, *) en sammansättningsalgebra .

En liknande algebra baserad på $\mathbb {R} ^{2}$ och komponentvisa operationer för addition och multiplikation, $(\mathbb {R } ^{2},+,\times ,xy),$ där xy är den kvadratiska formen på $\mathbb {R} ^{2},$ bildar också ett kvadratiskt mellanrum . Ringen isomorfism

$${\begin{aligned}D&\to \mathbb {R} ^{2}\\x+yj&\mapsto (xy,x +y)\end{aligned}}$$

relaterar proportionella kvadratiska former, men avbildningen är inte en isometri eftersom den multiplikativa identiteten (1, 1) av $\mathbb {R} ^{2}$ är på avståndet ${\sqrt {2 }}$ från 0, vilket är normaliserat i D .

Split-komplexa tal har många andra namn; se § Synonymer nedan. Se artikeln Motorvariabel för funktioner av ett delat-komplext tal.

Definition

Ett delat-komplext tal är ett ordnat par av reella tal, skrivna i formen

$$z=x+jy$$

där x och y är reella tal och den hyperboliska enheten j uppfyller

$$j^{2}=+1$$

I fältet för komplexa tal uppfyller den imaginära enheten $i^{2}=-1.$ Förändringen av tecken skiljer de delade-komplexa talen från de vanliga komplexa. Den hyperboliska enheten j är inte ett reellt tal utan en oberoende storhet.

Samlingen av alla sådana z kallas det split-komplexa planet . Addition och multiplikation av delade komplexa tal definieras av

$${\begin{aligned}(x+jy)+(u+jv)&=(x+u)+j(y+v)\\(x+jy)(u+jv)&=(xu +yv)+j(xv+yu).\end{aligned}}$$

Denna multiplikation är kommutativ , associativ och fördelar över addition.

Konjugat, modul och bilinjär form

Precis som för komplexa tal kan man definiera begreppet delat-komplext konjugat . Om

$$z=x+jy~,$$

definieras konjugatet av z som

$$z^{*}=x-jy~.$$

Konjugatet uppfyller liknande egenskaper som vanligt komplext konjugat. Nämligen,

$${\begin{aligned}(z+w)^{*}&=z^{*}+w^{*}\\(zw)^{*}&=z^{*}w^{ *}\\\left(z^{*}\right)^{*}&=z.\end{aligned}}$$

Dessa tre egenskaper antyder att det delade komplexa konjugatet är en automorfism av ordning 2.

Den kvadratiska modulen för ett delat-komplext tal $z=x+jy$ ges av den isotropiska kvadratiska formen

$$\lVert z\rVert ^{2}=zz^{*}=z^{*}z=x^{2}-y^{2}~.$$

Den har egenskapen sammansättning algebra :

$$\lVert zw\rVert =\lVert z\rVert \lVert w\rVert ~.$$

Denna kvadratiska form är dock inte positiv-definitiv utan har snarare signatur (1, −1) , så modulen är inte en norm .

Den tillhörande bilinjära formen ges av

$$\langle z,w\rangle =\operatörsnamn {\mathcal {R_{e }}} \left(zw^{*}\right)=\operatörsnamn {\mathcal {R_{e}}} \left(z^{*}w\right)=xu-yv~,$$

där $z=x+jy$ och $w=u+jv.$ Ett annat uttryck för kvadratmodulen är då

$$\lVert z\rVert ^{2}=\langle z,z\rangle ~.$$

Eftersom den inte är positiv-definitiv är denna bilinjära form inte en inre produkt ; ändå kallas den bilinjära formen ofta till som en obestämd inre produkt . Ett liknande missbruk av språket hänvisar till modulen som en norm.

Ett delat-komplext tal är inverterbart om och endast om dess modul inte är noll ( ${\displaystyle \lVert z\rVert \neq 0} ),$ alltså har tal av formen x ± jx ingen invers. Den multiplikativa inversen av ett inverterbart element ges av

$$z^{-1}={\frac {z^{*}}{{\lVert z\rVert }^{2}}}~.$$

Split-komplexa tal som inte är inverterbara kallas nollvektorer . Dessa är alla av formen ( a ± ja ) för något reellt tal a .

Den diagonala grunden

Det finns två icke-triviala idempotenta element som ges av $e={\tfrac {1}{2}}(1-j)$ och $e^{*}={\tfrac {1}{2}}(1+j).$ Kom ihåg att idempotent betyder att $ee=e$ och $e^{*}e^{*}=e^{*}.$ Båda dessa element är null:

$$\lVert e\rVert =\lVert e^{*}\rVert =e^{*}e=0~.$$

Det är ofta bekvämt att använda e och e ^∗ som en alternativ bas för det delade komplexa planet. Denna bas kallas diagonalbas eller nollbas . Det delade komplexa talet z kan skrivas i nollbasen som

$$z=x+jy=(xy)e+(x+y)e^{*}~.$$

Om vi ​​betecknar talet $z=ae+be^{*}$ för reella tal a och b med ( a , b ) så ges delad-komplex multiplikation med

$$\left(a_{1},b_{1}\right)\left(a_{2},b_{2}\right)=\left(a_{1}a_{2},b_{1} b_{2}\right)~.$$

Det delade komplexa konjugatet i diagonalbasen ges av

$$(a,b)^{*}=(b,a)$$

och modulen med

$$\lVert (a,b)\rVert =ab.$$

Isomorfi

Det här kommutativa diagrammet relaterar funktionen hos den hyperboliska versorn på D för att squeeze mappning σ tillämpad på $\mathbb {R} ^{2}$

På basis av {e, e*} blir det tydligt att de delade komplexa talen är ringisomorfa till den direkta summan $\mathbb {R} \oplus \mathbb {R}$ med addition och multiplikation definierade parvis.

Den diagonala basen för det delade komplexa talplanet kan anropas genom att använda ett ordnat par ( x , y ) för $z=x+jy$ och göra mappningen

$$(u,v)=(x,y){\begin{pmatrix}1&1\\1&-1\end{pmatrix}}=(x,y)S~.$$

Nu är kvadratformen $uv=(x+y)(xy)=x^{2}-y^{2}~.$ Dessutom,

$$(\cosh a,\sinh a){\begin{pmatrix}1&1\\1&-1\ end{pmatrix}}=\left(e^{a},e^{-a}\right)$$

så de två parametriserade hyperbolerna bringas i överensstämmelse med S .

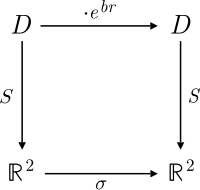
Åtgärden för hyperbolisk versor $e^{bj}\!$ motsvarar sedan under denna linjära transformation en squeeze-mappning

$$\sigma :(u,v)\mapsto \left(ru,{\frac {v}{r}}\right),\quad r=e^{b}~.$$

Även om de ligger i samma isomorphism klassificerar i kategorin ringar , skiljer sig det split-komplexa planet och den direkta summan av två reella linjer i sin layout i det kartesiska planet . Isomorfismen, som en plan avbildning, består av en moturs rotation med 45° och en utvidgning med √ 2 . Särskilt utvidgningen har ibland orsakat förvirring i samband med områden av en hyperbolisk sektor . I själva verket motsvarar hyperbolisk vinkel arean av en sektor i $\mathbb {R} \oplus \mathbb {R}$ -planet med dess "enhetscirkel" given av ${\displaystyle \{(a,b)\in \mathbb {R} \oplus \mathbb {R} :ab=1\}.} Den kontrakterade$ enheten hyperbel $\{\cosh a+j\sinh a:a\in \mathbb {R} \}$ av det delade komplexa planet har bara halva arean i spännvidden av en motsvarande hyperbolisk sektor. Sådan förvirring kan vidmakthållas när geometrin för det delade komplexa planet inte särskiljs från den för $\mathbb {R} \oplus \mathbb {R}$ .

Geometri

  Enhetshyperbel: ‖ z ‖ = 1

  Konjugerad hyperbel: ‖ z ‖ = −1

  Asymptoter: ‖ z ‖ = 0

Ett tvådimensionellt reellt vektorrum med Minkowskis inre produkt kallas (1 + 1) -dimensionellt Minkowskirum , ofta betecknat $\mathbb {R} ^{1,1}.$ Lika mycket av geometrin i det euklidiska planet $\mathbb {R} ^{2}$ kan beskrivas med komplexa tal, geometrin av Minkowski-planet $\mathbb {R} ^{1,1}$ kan beskrivas med delade-komplexa tal.

Uppsättningen av poäng

$$\left\{z:\lVert z\rVert ^{2}=a^{2}\right\}$$

är en hyperbel för varje icke-noll a i $\mathbb {R} .$ Hyperbeln består av en höger- och vänstergren som går genom ( a , 0) och (− a , 0) . Fallet a = 1 kallas enhetens hyperbel . Den konjugerade hyperbeln ges av

$$\left\{z:\lVert z\rVert ^{2}=-a^{2}\right\}$$

med en övre och nedre gren som går genom (0, a ) och (0, − a ) . Hyperbeln och den konjugerade hyperbeln är åtskilda av två diagonala asymptoter som bildar uppsättningen av nollelement:

$$\left\{z:\lVert z\rVert =0\right\}.$$

Dessa två linjer (kallas ibland nollkonen ) är vinkelräta i $\mathbb {R} ^{2}$ och har lutningar ±1.

Delade komplexa tal z och w sägs vara hyperboliskt-ortogonala om ⟨ z , w ⟩ = 0 . Även om det är analogt med vanlig ortogonalitet, särskilt som det är känt med aritmetik med vanliga komplexa tal, är detta tillstånd mer subtilt. Den utgör grunden för det simultana hyperplankonceptet i rumtiden.

Analogen till Eulers formel för de delade komplexa talen är

$$\exp(j\theta )=\cosh(\theta )+j\sinh(\theta ).$$

Denna formel kan härledas från en kraftserieexpansion med det faktum att cosh bara har jämna potenser medan den för sinh har udda potenser. För alla reella värden för den hyperboliska vinkeln θ har det delade komplexa talet λ = exp( jθ ) norm 1 och ligger på högra grenen av enhetens hyperbel. Tal som λ har kallats hyperboliska versors .

Eftersom λ har modul 1, multiplicerar man valfritt delat-komplext tal z med λ bevarar man modulen för z och representerar en hyperbolisk rotation (även kallad en Lorentz-boost eller en squeeze-mappning ). Multiplicering med λ bevarar den geometriska strukturen, tar hyperboler till sig själva och nollkonen till sig själv.

Mängden av alla transformationer av det delade komplexa planet som bevarar modulen (eller motsvarande den inre produkten) bildar en grupp som kallas den generaliserade ortogonala gruppen O(1, 1) . Denna grupp består av de hyperboliska rotationerna, som bildar en undergrupp betecknad SO ⁺ (1, 1) , kombinerat med fyra diskreta reflektioner som ges av

$z\mapsto \pm z$ och $z\mapsto \pm z^{*}.$

Den exponentiella kartan

$$\exp \colon (\mathbb {R} ,+)\to \mathrm {SO} ^{+}(1,1)$$

att skicka θ till rotation med exp( jθ ) är en gruppisomorfism eftersom den vanliga exponentialformeln gäller:

$$e^{j(\theta +\phi )}=e^{j\theta}e^{j\phi}.$$

Om ett delat-komplext tal z inte ligger på en av diagonalerna, så har z en polär nedbrytning .

Algebraiska egenskaper

I abstrakta algebratermer kan de delade komplexa talen beskrivas som kvoten för polynomringen $\mathbb {R} [x]$ av idealet som genereras av polynomet ${\ displaystil x^{2}-1,}$

$$\mathbb {R} [x]/(x^{2}-1).$$

Bilden av x i kvoten är den "imaginära" enheten j . Med denna beskrivning är det tydligt att de delade-komplexa talen bildar en kommutativ algebra över de reella talen. Algebra är inte ett fält eftersom nollelementen inte är inverterbara. Alla nollelement som inte är noll är nolldelare .

Eftersom addition och multiplikation är kontinuerliga operationer med avseende på planets vanliga topologi, bildar de delade komplexa talen en topologisk ring .

Algebra av delade-komplexa tal bildar en sammansättningsalgebra sedan

$\lVert zw\rVert =\lVert z\rVert \lVert w\rVert ~$ för alla nummer z och w .

Av definitionen är det uppenbart att ringen av delade komplexa tal är isomorf till gruppringen $\mathbb {R} [C^{2}]$ i den cykliska gruppen C ₂ över den reella nummer $\mathbb {R} .$

Matrisrepresentationer

Man kan enkelt representera delade-komplexa tal med matriser . Det delade komplexa talet $z=x+jy$ kan representeras av matrisen $z\mapsto {\begin{pmatrix}x&y\\y&x\end{pmatrix}}.$

Addition och multiplikation av delade komplexa tal ges sedan genom matrisaddition och multiplikation. Modulen för z ges av determinanten för motsvarande matris.

Faktum är att det finns många representationer av det delade komplexa planet i den fyrdimensionella ringen av 2x2 reella matriser. Identitetsmatrisens reella multipler bildar en reell linje i matrisringen M(2,R). Vilken som helst hyperbolisk enhet m tillhandahåller ett baselement med vilket den reella linjen kan förlängas till det delade komplexa planet. Matriserna

$m={\begin{pmatrix}a&c\\b&-a\end{pmatrix}}$ vilken kvadrat till identitetsmatrisen uppfyller ${\ displaystyle a^{2}+bc=1.}$

Till exempel, när a = 0, är ​​( b,c ) en punkt på standardhyperbeln. Mer generellt finns det en hyperyta i M(2,R) av hyperboliska enheter, varav vilken som helst tjänar som bas för att representera de delade komplexa talen som en subring av M(2,R).

Talet $z=x+jy$ kan representeras av matrisen $x\ I+y\ m.$

Historia

Användningen av delade komplexa tal går tillbaka till 1848 när James Cockle avslöjade sina tessariner . William Kingdon Clifford använde delade komplexa tal för att representera summan av snurr. Clifford introducerade användningen av delade-komplexa tal som koefficienter i en quaternionalgebra som nu kallas split-biquaternions . Han kallade dess element "motorer", en term parallellt med "rotor"-verkan av ett vanligt komplext tal taget från cirkelgruppen . För att utvidga analogin, kontrasterar funktioner hos en motorvariabel till funktioner hos en vanlig komplex variabel .

Sedan slutet av 1900-talet har multiplikationen med split-complex ofta setts som en Lorentz-förstärkning av ett rymdtidsplan . I den modellen representerar talet z = x + y j en händelse i ett spatio-temporal plan, där x mäts i nanosekunder och y i Mermins fötter . Framtiden motsvarar kvadranten av händelser { z : | y | < x } , som har den delade komplexa polära nedbrytningen $z=\rho e^{aj}\!$ . Modellen säger att z kan nås från origo genom att gå in i en referensram med hastighet a och vänta ρ nanosekunder. Den delade-komplexa ekvationen

$$e^{aj}\ e^{bj}=e^{(a+b)j}$$

att uttrycka produkter på enhetshyperbolen illustrerar additiviteten hos hastigheter för kolinjära hastigheter. Samtidigt av händelser beror på snabbhet a ;

$$\{z=\sigma je^{aj}:\sigma \in \mathbb {R} \}$$

är händelseraden samtidigt med ursprunget i referensramen med snabbhet a .

Två händelser z och w är hyperboliskt-ortogonala när $z^{*}w+zw^{*}=0.$ Kanoniska händelser exp( aj ) och j exp( aj ) är hyperboliska ortogonala och ligger på axlarna för en referensram där händelserna samtidigt med origo är proportionella mot j exp( aj ) .

1933 använde Max Zorn de delade oktonionerna och noterade kompositions-algebra- egenskapen. Han insåg att Cayley-Dickson-konstruktionen , som användes för att generera divisionalgebror, kunde modifieras (med en faktor gamma, γ ) för att konstruera andra sammansättningsalgebror inklusive split-octonions. Hans innovation vidmakthölls av Adrian Albert , Richard D. Schafer och andra. Gammafaktorn, med R som basfält, bygger uppdelade komplexa tal som en sammansättningsalgebra. Genom att granska Albert för matematiska recensioner , skrev NH McCoy att det fanns en "introduktion av några nya algebror av ordningen 2 ^e över F som generaliserade Cayley–Dickson-algebror." Att ta F = R och e = 1 motsvarar algebra i denna artikel.

År 1935 utvecklade JC Vignaux och A. Durañona y Vedia den delade komplexa geometriska algebra och funktionsteorin i fyra artiklar i Contribución a las Ciencias Físicas y Matemáticas, National University of La Plata , República Argentina (på spanska). Dessa expository och pedagogiska uppsatser presenterade ämnet för bred uppskattning.

1941 använde EF Allen den split-komplexa geometriska aritmetiken för att fastställa niopunktshyperbeln i en triangel inskriven i zz ^∗ = 1 .

1956 publicerade Mieczyslaw Warmus "Calculus of Approximations" i Bulletin de l'Académie polonaise des sciences (se länk i Referenser). Han utvecklade två algebraiska system, som var och en kallade "ungefärliga tal", varav det andra bildar en riktig algebra. DH Lehmer granskade artikeln i Mathematical Reviews och observerade att detta andra system var isomorft till de "hyperboliska komplexa" talen, ämnet för denna artikel.

1961 fortsatte Warmus sin utläggning och hänvisade till komponenterna i ett ungefärligt antal som mittpunkt och radie av det angivna intervallet.

Synonymer

Olika författare har använt en stor variation av namn för de delade komplexa talen. Några av dessa inkluderar:

• ( riktiga ) tessariner , James Cockle (1848)
• ( algebraiska ) motorer , WK Clifford (1882)
• hyperboliska komplexa tal , JC Vignaux (1935)
• bireala tal , U. Bencivenga (1946)
• approximative numbers , Warmus (1956), för användning i intervallanalys
• dubbelnummer , IM Yaglom (1968), Kantor och Solodovnikov (1989), Hazewinkel (1990), Rooney (2014)
• anormala-komplexa tal , W. Benz (1973)
• perplex numbers , P. Fjelstad (1986) och Poodiack & LeClair (2009)
• kontrakomplex eller hyperbolisk , Carmody (1988)
• Lorentz nummer , FR Harvey (1990)
• hyperboliska tal , G. Sobczyk (1995)
• parakomplexa tal , Cruceanu, Fortuny & Gadea (1996)
• halvkomplexa tal , F. Antonuccio (1994)
• split binarions , K. McCrimmon (2004)
• split-complex numbers , B. Rosenfeld (1997)
• rumtidsnummer , N. Borota (2000)
• Studienummer , P. Lounesto (2001)
• tvåkomplexa tal , S. Olariu (2002)

Se även

• Minkowski utrymme
• Split-quaternion
• Hyperkomplext tal

Vidare läsning

• Bencivenga, Uldrico (1946) "Sulla rappresentazione geometrica delle algebre doppie dotate di modulo", Atti della Reale Accademia delle Scienze e Belle-Lettere di Napoli , Ser (3) v.2 No7. MR 0021123 .
• Walter Benz (1973) Vorlesungen uber Geometrie der Algebren , Springer
• NA Borota, E. Flores och TJ Osler (2000) "Spacetime numbers the easy way", Mathematics and Computer Education 34: 159–168.
• NA Borota och TJ Osler (2002) "Funktioner av en rumtidsvariabel", Mathematics and Computer Education 36: 231–239.
• K. Carmody, (1988) "Circular and hyperbolic quaternions, octonions and sedenions", Appl. Matematik. Comput. 28:47–72.
• K. Carmody, (1997) "Cirkulära och hyperboliska kvaternioner, oktonioner och sedenioner – ytterligare resultat", Appl. Matematik. Comput. 84:27–48.
• William Kingdon Clifford (1882) Mathematical Works , AW Tucker-redaktör, sidan 392, "Further Notes on Biquaternions"
• V.Cruceanu, P. Fortuny & PM Gadea (1996) A Survey on Paracomplex Geometry , Rocky Mountain Journal of Mathematics 26(1): 83–115, länk från Project Euclid .
• De Boer, R. (1987) "An also known as list for perplex numbers", American Journal of Physics 55(4):296.
• Anthony A. Harkin & Joseph B. Harkin (2004) Geometry of Generalized Complex Numbers , Mathematics Magazine 77(2):118–29.
•   F. Reese Harvey. Spinorer och kalibreringar. Academic Press, San Diego. 1990. ISBN 0-12-329650-1 . Innehåller en beskrivning av normerade algebror i obestämd signatur, inklusive Lorentz-talen.
• Hazewinkle, M. (1994) "Double and dual numbers", Encyclopaedia of Mathematics , Soviet/AMS/Kluwer, Dordrect.
•   Kevin McCrimmon (2004) A Taste of Jordan Algebras , pp 66, 157, Universitext, Springer ISBN 0-387-95447-3 MR 2014924
• C. Musès, "Applied hypernumbers: Computational concepts", Appl. Matematik. Comput. 3 (1977) 211-226.
• C. Musès, "Hypernumbers II – Ytterligare begrepp och beräkningstillämpningar", Appl. Matematik. Comput. 4 (1978) 45-66.
•   Olariu, Silviu (2002) Complex Numbers in N Dimensions , Kapitel 1: Hyperbolic Complex Numbers in Two Dimensions, sidorna 1–16, North-Holland Mathematics Studies #190, Elsevier ISBN 0-444-51123-7 .
• Poodiack, Robert D. & Kevin J. LeClair (2009) "Fundamental theorems of algebra for the perplexes", The College Mathematics Journal 40(5):322–35.
• Isaak Yaglom (1968) Complex Numbers in Geometry , översatt av E. Primrose från 1963 ryskt original, Academic Press , s. 18–20.
•   J. Rooney (2014). "Generaliserade komplexa tal i mekanik". I Marco Ceccarelli och Victor A. Glazunov (red.). Advances on Theory and Practice of Robots and Manipulators: Proceedings of Romansy 2014 XX CISM-IFToMM Symposium on Theory and Practice of Robots and Manipulators . Mekanismer och maskinvetenskap. Vol. 22. Springer. s. 55–62. doi : 10.1007/978-3-319-07058-2_7 . ISBN 978-3-319-07058-2 .