Lune (geometri)
|

|

|
|
|
|
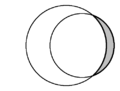
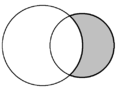
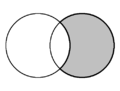
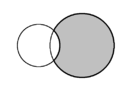
| I plan geometri kallas halvmånen som bildas av två skärande cirklar en lune . I varje diagram finns två lunes, och en är skuggad i grått. | ||
I plan geometri är en lune (från latin luna "måne") den konkav-konvexa regionen som begränsas av två cirkulära bågar . Den har en gränsdel för vilken det förbindande segmentet av två närliggande punkter rör sig utanför området och ett annat gränsparti för vilket det anslutande segmentet av två närliggande punkter ligger helt inom området. En konvex-konvex region kallas en lins .
Formellt är en lune det relativa komplementet till en skiva i en annan (där de skär varandra men ingen är en delmängd av den andra). Alternativt, om och är diskar, då är en lune.
Squaring the lune
På 500-talet f.Kr. visade Hippokrates från Chios att Hippokrates Lune och två andra luner kunde kvadratiseras exakt (omvandlas till en kvadrat med samma yta) med rätsida och kompass . År 1766 listade den finske matematikern Daniel Wijnquist, med citat av Daniel Bernoulli , alla fem geometriska kvadratiska lunes, vilket lade till de som Hippokrates kände till. 1771 Leonard Euler ett allmänt tillvägagångssätt och fick en viss ekvation till problemet. 1933 och 1947 bevisades det av Nikolai Chebotaryov och hans elev Anatolij Dorodnov att dessa fem är de enda fyrkantiga lunorna.
Område
Arean av en luna som bildas av cirklar med radier a och b ( b>a ) med avstånd c mellan deras centra är
där är den inversa funktionen av secant-funktionen , och där
är arean av en triangel med sidorna a, b och c .
Se även
externa länkar
- The Five Squarable Lunes på MathPages





