Modern triangelgeometri

Emile Lemoine (1840–1912)

Inom matematiken är modern triangelgeometri , eller ny triangelgeometri , den kunskapsmassa som relaterar till egenskaperna hos en triangel som upptäckts och utvecklats ungefär sedan början av den sista fjärdedelen av artonhundratalet. Trianglar och deras egenskaper var föremål för undersökning sedan åtminstone Euklids tid . Faktum är att Euklids element innehåller en beskrivning av de fyra speciella punkterna – centroid , incenter , circumcenter och ortocenter – associerade med en triangel. Även om Pascal och Ceva på 1600-talet, Euler på 1700-talet och Feuerbach på 1800-talet och många andra matematiker hade gjort viktiga upptäckter angående triangelns egenskaper, var det publiceringen 1873 av en artikel av Emile Lemoine (1840 ) –1912) med titeln "På en anmärkningsvärd punkt i triangeln" som enligt Nathan Altschiller-Court ansågs ha "lagt grunden ... till triangelns moderna geometri som helhet." American Mathematical Monthly , där mycket av Lemoines arbete publiceras, förklarade att "Ingen av dessa [geometrar] mer än Émile-Michel-Hyacinthe Lemoine är tack vare äran att starta denna rörelse av modern triangelgeometri". Publiceringen av denna tidning orsakade ett anmärkningsvärt uppsving av intresse för att undersöka egenskaperna hos triangeln under den sista fjärdedelen av 1800-talet och de första åren av 1900-talet. En hundra sidor lång artikel om triangelgeometri i Kleins Encyclopedia of Mathematical Sciences publicerad 1914 vittnar om detta uppsving av intresse för triangelgeometri.

I de tidiga dagarna hänvisade uttrycket "ny triangelgeometri" endast till den uppsättning intressanta föremål som associerades med en triangel som Lemoine-punkten , Lemoine-cirkeln, Brocard-cirkeln och Lemoine-linjen . Senare utvecklades teorin om överensstämmelse som var en utlöpare av teorin om geometriska transformationer för att ge koherens till de olika isolerade resultaten. Med sin utveckling indikerade uttrycket "ny triangelgeometri" inte bara de många anmärkningsvärda föremålen som är förknippade med en triangel utan också de metoder som används för att studera och klassificera dessa föremål. Här är en definition av triangelgeometri från 1887: "När vi ges en punkt M i triangelns plan, kan vi alltid hitta en andra punkt M' som motsvarar den första enligt en föreställd geometri. lag; dessa två punkter har geometriska relationer emellan vars enkelhet beror på det mer eller mindre lyckliga valet av den lag som förenar dem och varje geometrisk lag ger upphov till en metod för omvandling av ett sätt att konjugera som det återstår att studera." (Se konferensbidraget med titeln "Att lära ut nya geometriska metoder med en antik figur på 1800- och 1900-talet: den nya triangelgeometrin i läroböcker i Europa och USA (1888–1952)" av Pauline Romera-Lebret presenterad 2009.)

Denna eskalering av intresse kollapsade dock snart och triangelgeometrin försummades helt fram till 1900-talets sista år. I sin "Development of Mathematics" Eric Temple Bell sin bedömning av statusen för modern triangelgeometri 1940 så här: "1900-talets geometrar har för länge sedan fromt tagit bort alla dessa skatter till geometrimuseet där historiens damm dämpade snabbt deras lyster." (The Development of Mathematics, s. 323) Philip Davis har föreslagit flera orsaker till det minskade intresset för triangelgeometri. Dessa inkluderar:

Känslan av att ämnet är elementärt och av låg yrkesstatus.
Uttömningen av dess metodiska möjligheter.
Den visuella komplexiteten hos de så kallade djupare resultaten av ämnet.
Nedgraderingen av det visuella till förmån för det algebraiska.
Brist på kopplingar till andra områden.
Tävla med andra ämnen med ett starkt visuellt innehåll som tesselleringar , fraktaler , grafteori , etc.

En ytterligare väckelse av intresse bevittnades med tillkomsten av den moderna elektroniska datorn . Triangelgeometrin har återigen blivit ett aktivt forskningsområde som bedrivs av en grupp dedikerade geometrar. Som ett symbol för denna väckelse kan man peka på formuleringen av begreppet ett " triangelcentrum " och Clark Kimberlings sammanställning av ett uppslagsverk över triangelcentrum som innehåller en förteckning över nästan 50 000 triangelcentrum och deras egenskaper och även sammanställningen av en katalog av triangelkubiker med detaljerade beskrivningar av flera egenskaper på mer än 1200 triangelkubiker. Open access-tidskriften Forum Geometricorum som grundades av Paul Yiu från Florida Atlantic University 2001 gav också en enorm drivkraft för att främja denna nyfunna entusiasm för triangelgeometri. Tyvärr, sedan 2019, tar tidskriften inte emot bidrag även om tidigare nummer fortfarande finns tillgängliga online.

Lemoine-geometrin

Lemoine punkt

För en given triangel ABC med tyngdpunkten G är symmedianen genom vertex reflektionen av linjen AG i bisektrisen av vinkeln A. Det finns tre symmedianer för en triangel en som går genom varje vertex. De tre symmedianerna är samtidiga och samtidighetspunkten, vanligen betecknad med K, kallas Lemoine- punkten eller symmedianpunkten eller Grebe-punkten i triangeln ABC. Om sidolängderna för triangeln ABC är a , b , c är de baricentriska koordinaterna för Lemoinepunkten a ² : b ² : c ² . Det har beskrivits som "en av kronjuvelerna i modern geometri". Det finns flera tidigare hänvisningar till denna punkt i den matematiska litteraturen som finns tillgängliga i John Mackays historia av symmedianpunkten.

I själva verket är samtidigheten av symmedianerna ett specialfall av ett mer allmänt resultat: För vilken punkt P som helst i triangelns ABC-plan är isogonalerna för linjerna AP, BP, CP samtidiga, AP:s isogonal (respektive BP, CP) är reflektionen av linjen AP i bisektrisen av vinkeln A (respektive B, C). Punkten för samtidighet kallas det isogonala konjugatet av P. I denna terminologi är Lemoine-punkten det isogonala konjugatet av tyngdpunkten.

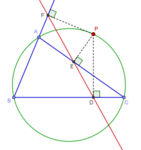
Lemoine cirklar

Skärningspunkterna för linjerna genom Lemoine-punkten i en triangel ABC parallellt med triangelns sidor ligger på en cirkel som kallas den första Lemoine-cirkeln i triangeln ABC. Mitten av den första Lemoine-cirkeln ligger mitt emellan triangelns circumcenter och lemoine-punkten,

Skärningspunkterna för antiparallellerna till sidorna av triangeln ABC genom Lemoine-punkten i en triangel ABC ligger på en cirkel som kallas den andra Lemoine-cirkeln eller cosinuscirkeln för triangeln ABC. Namnet "cosinuscirkel" beror på egenskapen hos den andra Lemoine-cirkeln att längderna på segmenten som fångas upp av cirkeln på sidorna av triangeln är proportionell mot cosinus i vinklarna mitt emot sidorna. Mitten av den andra Lemoine-cirkeln är Lemoine-punkten.

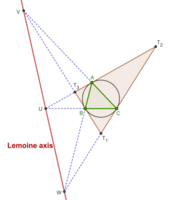
Lemoine axel

Varje triangel ABC och dess tangentiella triangel är i perspektiv och perspektivaxeln kallas Lemoine-axeln i triangeln ABC. Det är den trilinjära polären för den symmedianska punkten för triangeln ABC och även den polära av K med avseende på omkretsen av triangeln ABC.

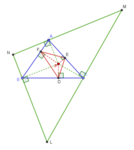
En triangel med medianer (svart), vinkelhalveringslinjer (prickade) och symmedianer (röd). Symmedianerna skär i symmedianpunkten (betecknad med L i figuren), vinkelhalveringslinjerna i mitten I och medianerna i tyngdpunkten G.
Första Lemoine cirkel av triangel ABC. Lemoine-punkten K, mitten I, tyngdpunkten G och linjerna genom K parallella med sidorna visas också.
Andra Lemoine cirkel av triangel ABC. Lemoine-punkten K, mitten I, tyngdpunkten G och linjerna genom K antiparrallellt mot sidorna visas också.
Lemoine axel av triangel ABC. Den tangentiella triangeln visas också.

Tidig modern triangelgeometri

En snabb blick in i den moderna triangelgeometrins värld som den existerade under toppen av intresset för triangelgeometri efter publiceringen av Lemoines papper presenteras nedan. Denna presentation är till stor del baserad på de ämnen som diskuteras i William Gallatlys bok som publicerades 1910 och Roger A Johnsons bok som först publicerades 1929.

Poristiska trianglar

Två trianglar sägs vara poristiska trianglar om de har samma incirkel och omsluten cirkel. Givet en cirkel med centrum O och radie R och en annan cirkel med centrum I och radie r , finns det ett oändligt antal trianglar ABC med Cirkel O( R ) som omsluten cirkel och I( r ) som i cirkel om och endast om {{ { 1}}} . Dessa trianglar bildar ett poristiskt system av trianglar. Lokalerna för vissa speciella punkter som tyngdpunkt som referenstriangeln spårar de olika trianglarna poristiska med det visar sig vara cirklar och punkter.

Simson-linjen

För vilken punkt P som helst på omkretsen av triangeln ABC, är fötterna på vinkelräta från P till sidorna av triangeln ABC kolinjära och kollinearitetslinjen är den välkända Simson-linjen för P.

Pedal- och antipedaltrianglar

Givet en punkt P, låt foten av vinkelräta från P till sidorna av triangeln ABC vara D, E, F. Triangeln DEF kallas pedaltriangeln av P. Antipedaltriangeln av P är triangeln som bildas av linjerna genom A, B, C vinkelrätt mot PA, PB, PC respektive. Två punkter P och Q kallas motpunkter om pedaltriangeln i P är homotetisk med antipedaltriangeln på Q och pedaltriangeln på Q är homotetisk med antipedaltriangeln på P.

Ortopolen

Givet vilken linje l som helst , låt P, Q, R vara foten av vinkelräta från hörnen A, B, C i triangeln ABC till l . Linjerna genom P. Q, R vinkelräta respektive mot sidorna BC, CA, AB är samtidiga och samtidighetspunkten är ortopolen för linjen l med avseende på triangeln ABC. I modern triangelgeometri finns det en stor mängd litteratur som handlar om egenskaper hos ortopoler.

Brocard poäng

Låt av cirklar beskrivas på sidorna BC, CA, AB av triangeln ABC vars yttre segment innehåller de två triaderna av vinklarna C, A, B och B, C, A respektive. Varje triad av cirklar som bestäms av en triad av vinklar skär varandra vid en gemensam punkt, vilket ger två sådana punkter. Dessa punkter kallas Brocard-punkterna i triangeln ABC och betecknas vanligtvis med $\Omega ,\Omega ^{\prime }$ . Om P är den första Brocard-punkten (som är Brocard-punkten som bestäms av den första triaden av cirklar) så är vinklarna PBC, PCA och PAB lika med varandra och den gemensamma vinkeln kallas Brocard-vinkeln för triangeln ABC och betecknas vanligtvis av $\omega$ Brocard-vinkeln ges av

\cot \omega =\cot A+\cot B+\cot C.

Brocard-spetsarna och Brocard-vinklarna har flera intressanta egenskaper.

Några bilder

Två poristiska trianglar ABC och A'B'C' med avseende på cirklarna I( r ) och O( R )
Simson linje av P
Pedaltriangel (DEF) och antipedaltriangel (LMN) för P
Ortopol av linje l
Första Brocard-punkten i triangeln ABC

Samtida modern triangelgeometri

Triangel mitt

En av de viktigaste idéerna som har dykt upp under återupplivandet av intresset för triangelgeometri under de sista åren av 1900-talet är begreppet triangelcentrum . Detta koncept som introducerades av Clark Kimberling 1994 förenade i en uppfattning de väldigt många speciella och anmärkningsvärda punkter som är förknippade med en triangel. Sedan introduktionen av denna idé är nästan ingen diskussion om något resultat associerat med en triangel komplett utan en diskussion om hur resultatet hänger ihop med triangelns centra.

Definition av triangelcentrum

En realvärderad funktion f av tre reella variabler a , b , c kan ha följande egenskaper:

Homogenitet: f ( ta , tb , tc ) = t ⁿ f ( a , b , c ) för någon konstant n och för alla t > 0.
Bisymmetri i den andra och tredje variabeln: f ( a , b , c ) = f ( a , c , b ).

Om ett f som inte är noll har båda dessa egenskaper kallas det en triangelcentrumfunktion . Om f är en triangelcentrumfunktion och a , b , c är sidolängderna på en referenstriangel så är den punkt vars trilinjära koordinater är f ( a , b , c ) : f ( b , c , a ): f ( c ) , a , b ) kallas ett triangelcentrum .

Clark Kimberling upprätthåller en webbplats ägnad åt ett kompendium av triangelcentra. Webbplatsen som heter Encyclopedia of Triangle Centers har definitioner och beskrivningar av nästan 50 000 triangelcentra.

Centrallinje

En annan förenande föreställning om samtida modern triangelgeometri är en central linje . Detta koncept förenar de flera speciella raka linjerna som är förknippade med en triangel. Begreppet centrallinje är också relaterat till begreppet triangelcentrum.

Definition av central linje

Låt ABC vara en plan triangel och låt ( x : y : z ) vara de trilinjära koordinaterna för en godtycklig punkt i triangelns ABC -plan .

ABC- plan vars ekvation i trilinjära koordinater har formen

f ( a , b , c ) x + g ( a , b , c ) y + h ( a , b , c ) z = 0

där punkten med trilinjära koordinater ( f ( a , b , c ) : g ( a , b , c ) : h ( a , b , c ) ) är ett triangelcentrum, är en central linje i triangelns ABC relativa plan till triangeln ABC .

Geometrisk konstruktion av central linje

Låt X vara valfri triangelcentrum i triangeln ABC .

Rita linjerna AX , BX och CX och deras reflektioner i de inre halvledarna av vinklarna vid hörnen A , B , C respektive.
De reflekterade linjerna är samtidiga och punkten för samtidighet är det isogonala konjugatet Y av X .
Låt cevianerna AY , BY , CY möta de motsatta sidlinjerna av triangeln ABC vid A' , B' , C' respektive. Triangeln A ' B ' C ' är den cevianska triangeln för Y.
Triangeln ABC och den cevianska triangeln A ' B ' C ' är i perspektiv och låter DEF vara perspektivaxeln för de två trianglarna. Linjen DEF är den trilinjära polära punkten Y . Linjen DEF är den centrala linjen associerad med triangelns centrum X .

Triangelkoner

En triangelkonisk är en konik i referenstriangelns plan och associerad med den på något sätt. Till exempel är den omslutna cirkeln och incirkeln av referenstriangeln triangelkoniska. Andra exempel är Steinerellipsen som är en ellips som passerar genom hörnen och som har sitt centrum i referenstriangelns tyngdpunkt , Kiepert-hyperbolen som är en kon som passerar genom hörnen, tyngdpunkten och ortocentrum i referenstriangeln och Artzt paraboler som är paraboler som berör två sidlinjer i referenstriangeln vid triangelns hörn. Några nyligen studerade triangelkoner inkluderar Hofstadter-ellipser och yff-koniker . Det finns dock ingen formell definition av terminologin för triangelkonisk i litteraturen; det vill säga relationerna en kägel bör ha med referenstriangeln för att kvalificera den för att kallas en triangelkonisk har inte formulerats exakt. WolframMathWorld har en sida med titeln "Triangel koniska" som ger en lista med 42 objekt (inte alla är koniska) utan att ge en definition av triangelkoniska.

Steiner ellips
Artz paraboler
Kiepert hyperbel

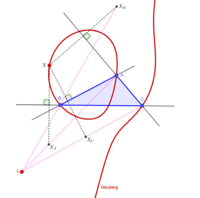
Triangelkubik

Kubiska kurvor uppstår naturligt i studiet av trianglar. Till exempel, platsen för en punkt P i planet för referenstriangeln ABC så att, om reflektionerna av P i sidolinjerna av triangeln ABC är P a , P b , P _c , _då linjerna _AP a _, BP _b och CP _c är samtidiga är en kubisk kurva som heter Neuberg kubisk . Det är den första kuben som listas i Bernard Gilberts Catalog of Triangle Cubics . Denna katalog listar mer än 1200 triangelkubiker med information om varje kurva, såsom kurvans barycentriska ekvation, triangelcentrum som ligger på kurvan, kurvans lokusegenskaper och referenser till litteratur om kurvan.

Neuberg cubic ( K001 )
McCay kubisk med sina tre samstämmiga asymptoter ( K003 )
Tucker cubic ( K011 )

Datorer i triangelgeometri

Datorernas intåg hade ett avgörande inflytande på utvecklingen av intresset för triangelgeometri som man såg under 1900-talets sista år och det nuvarande århundradets första år. Några av de sätt som datorerna hade påverkat denna kurs har beskrivits av Philip Davis. Datorer har använts för att generera nya resultat i triangelgeometri. En enkätartikel publicerad 2015 ger en redogörelse för några av de viktiga nya resultat som upptäckts av datorprogrammet "Dircoverer". Följande exempel på satser ger en smak av de nya resultaten som upptäckts av Discoverer.

Sats 6.1 Låt P och Q vara punkter, varken ligger på en sidolinje av triangeln ABC. Om P och Q är isogonala konjugat med avseende på ABC, så ligger Ceva-produkten av deras komplement på Kiepert-hyperbolen.
Sats 9.1. Yff -centrum för kongruens är det inre liknelsecentrumet för incirkeln och den omslutna cirkeln med avseende på pedaltriangeln i incentret.
Lestercirkeln är cirkeln som passerar genom circumcenter , niopunktscentrum och de yttre och inre Fermatpunkterna. En generaliserad Lestercirkel är en cirkel som passerar genom minst fyra triangelcentrum. Discoverer har upptäckt flera generaliserade Lester-cirklar.

Sava Grozdev, Hiroshi Okumura, Deko Dekov upprätthåller en webbportal dedikerad till datorupptäckt uppslagsverk av euklidisk geometri.

Ytterligare läsning

John Mackay (1896). "Symmedianer av en triangel och deras åtföljande cirklar" ( PDF) . Proceedings of the Edinburgh Math. Soc . XIV : 37–103 . Hämtad 7 januari 2022 .
William Gallatly (1910). Triangelns moderna geometri . London: Francis Hodgson . Hämtad 4 januari 2022 .
Ross Honsberger (1995). Episoder i 1800- och 1900-talets euklidiska geometri . Mathematical Association of America.
Roger A Johnson (31 augusti 2007). Avancerad euklidisk geometri . Dover Publications Inc. ISBN 978-0486462370 .
HSM Coexter (5 september 1996). Geometri Revisited . Mathematical Association of America. ISBN 0883856190 .
Altshiller-Court, Nathan (1952). College geometri; en introduktion till triangelns och cirkelns moderna geometri . New York: Barnes & Noble . Hämtad 10 januari 2022 .
Kimberling, C (1998). "Triangelcentra och centraltrianglar". kongr. Nummer. : 1–295.
Paul Yiu (december 2012). Introduktion till triangelns geometri (PDF) . Institutionen för matematik Florida Atlantic University . Hämtad 5 januari 2022 .
Scott, Charlotte Angas (1894). En inledande redogörelse för vissa moderna idéer och metoder inom plananalytisk geometri . London: Macmillan och Co. Hämtad 10 januari 2022 .