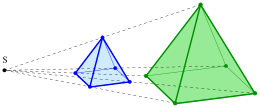
Homoteti

Homoteti: Exempel med $k>0$ För $k=1$ får man identiteten (ingen punkt flyttas), för $k>1$ en förstoring för $k<1$ en minskning

Exempel med $k<0$ För $k=-1$ får man en punktreflektion vid punkt $S$

Homotet av en pyramid

Inom matematik är en homoteti (eller homoteti eller homogen utvidgning ) en transformation av ett affint utrymme som bestäms av en punkt S som kallas dess mittpunkt och ett tal som inte är noll kallat dess förhållande , vilket skickar punkt $X$ till en punkt $X'$ av regeln

${\overrightarrow {SX'}}=k{\overrightarrow {SX}}$ för ett fast tal $k\neq 0$ .

Använda positionsvektorer:

$\mathbf {x} '=\mathbf {s} +k(\mathbf {x} -\mathbf {s} )$ .

I fallet med $S=O$ (Ursprung):

$\mathbf {x} '=k\mathbf {x}$ ,

som är en enhetlig skalning och visar innebörden av speciella val för $k$ :

för $k=1$ får man identitetskartläggningen ,

för $k=-1$ får man reflektionen i mitten,

För $1/k$ får man den inversa mappningen definierad av $k$ .

I euklidisk geometri är homoteter likheterna som fixerar en punkt och antingen bevarar (om $k>0$ ) eller vänder (om $k<0$ ) riktningen för alla vektorer. Tillsammans med översättningarna bildar alla homoter av ett affint (eller euklidiskt) rum en grupp , gruppen av utvidgningar eller homotetiska översättningar . Dessa är just de affina transformationerna med egenskapen att bilden av varje linje g är en linje parallell med g .

I projektiv geometri är en homothetic transformation en likhetstransformation (dvs fixerar en given elliptisk involution) som lämnar linjen vid oändligheten punktvis invariant .

multiplicerar en homotet med förhållandet $k$ avstånden mellan punkter med $|k|$ , ytor med $k^{2}$ och volymer med $|k|^{3}$ . Här är $k$ förhållandet mellan förstorings- eller utvidgningsfaktor eller skalfaktor eller likhetsförhållande . En sådan transformation kan kallas en förstoring om skalfaktorn överstiger 1. Den ovan nämnda fixpunkten S kallas homotetisk centrum eller likhetscentrum eller likhetscentrum .

Termen, myntad av den franske matematikern Michel Chasles , kommer från två grekiska element: prefixet homo- ( όμο ), som betyder "liknande", och tes ( Θέσις ), som betyder "position". Den beskriver förhållandet mellan två figurer med samma form och orientering. Till exempel kan två ryska dockor som tittar åt samma håll anses vara homotetiska.

Homoteties används för att skala innehållet på datorskärmar; till exempel smartphones, bärbara datorer och bärbara datorer.

Egenskaper

Följande egenskaper gäller i alla dimensioner.

Kartläggning av linjer, linjesegment och vinklar

En homotet har följande egenskaper:

• En linje avbildas på en parallell linje. Därför: vinklarna förblir oförändrade.
• Förhållandet mellan två linjesegment bevaras.

Båda fastigheterna visar:

• En homoteti är en likhet .

Härledning av egenskaperna: För att göra beräkningar lätta antas att mitten $S$ är ursprunget: $\mathbf {x} \to k\mathbf {x}$ . En linje $g$ med parametrisk representation $\mathbf {x} =\mathbf {p} +t\mathbf {v}$ mappas till punktmängden $g'$ med ekvation $\mathbf {x} =k(\mathbf {p} +t\mathbf {v} )=k\mathbf { p} +tk\mathbf {v}$ , som är en linje parallell med $g$ .

Avståndet mellan två punkter $P:\mathbf {p} ,\;Q:\mathbf {q}$ är $|\mathbf {p} -\mathbf {q} |$ och $|k\mathbf {p} -k\mathbf {q} |=|k||\mathbf {p} -\mathbf {q} |$ avståndet mellan deras bilder. Därför förhållandet (kvoten) mellan två linjesegment oförändrat .

I fallet $S\neq O$ är beräkningen analog men lite omfattande.

Konsekvenser: En triangel avbildas på en liknande . Den homotetiska bilden av en cirkel är en cirkel. Bilden av en ellips är en liknande bild. dvs förhållandet mellan de två axlarna är oförändrat.

Med interceptsats

Grafiska konstruktioner

med hjälp av interceptsatsen

Om för en homoteti med mitten $S$ ges bilden $Q_{1}$ av en punkt ${\displaystyle P_{1}} ( se diagram) så är bilden$${\ displaystyle Q_{2}} av$$SP_{1}$ andra punkt ${\displaystyle P_{2}} ,$ som inte ligger på linjen kan konstrueras grafiskt med hjälp av interceptsatsen: ${\ displaystyle Q_{2}}$ är den gemensamma punkten de två linjerna ${\overline {P_{1}P_{2}}}$ och ${\overline {SP_{ 2}}}$ . Bilden av en punkt kolinjär med $P_{2},Q_{2}$$\displaystyle P_{1},Q_{1}}$ kan bestämmas med .

Strömavtagare

Geometrisk bakgrund

Strömavtagare 3d-rendering

med hjälp av en strömavtagare

Innan datorer blev allestädes närvarande gjordes skalningar av ritningar med hjälp av en strömavtagare , ett verktyg som liknar en kompass .

Konstruktion och geometrisk bakgrund:

1. Ta 4 stavar och sätt ihop ett mobilt parallellogram med hörn $P_{0},Q_{0},H,P$ så att de två stavarna möts vid $Q_{0}$ är förlängda i andra änden som visas i diagrammet. Välj förhållandet $k$ .
2. Markera de två punkterna ${\displaystyle S,Q} på de förlängda stavarna$ så att $|SQ_{0}|=k|SP_{0}|$ och $|QQ_{0}|=k|HQ_{0}|$ . Detta är fallet om ${\displaystyle |SQ_{0}|={\tfrac {k}{k-1}}|P_{0}Q_{0}|.} ($ Istället för $k$ platsen för mitten ${ \displaystyle S}$ kan föreskrivas. I detta fall är förhållandet ${\displaystyle k=|SQ_{0}|/|SP_{0}|} .$ )
3. Fäst de rörliga stängerna roterbara vid punkt $S$ .
4. Variera platsen för punkt $P$ och markera vid varje tidpunkt $Q$ .

På grund av ${\displaystyle |SQ_{0}|/|SP_{0}|=|Q_{0}Q|/|PP_{0}|} ($ se diagram) man får från skärningssatsen att punkterna $S,P,Q$ är kolinjära (ligger på en linje) och ekvation $|SQ|=k|SP|$ håller. Det visar: mappningen $P\to Q$ är en homotety med mitten $S$ och förhållandet $k$ .

Sammansättning

Sammansättningen av två homoter med mittpunkter $S_{1},S_{2}$ och förhållanden $k_{1}=2,k_{2}=0{.}3$ mappning $P_{i}\to Q_{i}\to R_{i}$ är återigen en homotet med dess centrum $S_{3}$ på raden ${\overline {S_{1}S_{2}}}$ med förhållandet $k\cdot l=0{.}6$ .

• Sammansättningen av två homoter med samma centrum $S$ är återigen en homoteti med mitten $S$ . Homoteterna med mitten $S$ bildar en grupp .
• Sammansättningen av två homoter med olika centra $S_{1},S_{2}$ och dess förhållanden $k_{1},k_{2}$ är

i fallet $k_{1}k_{2}\neq 1$ en homotet med centrum på linjen ${\overline {S_{1}S_{2 }}}$ och förhållandet $k_{1}k_{2}$ eller

i fallet $k_{1}k_{2}=1$ en översättning i riktning ${\overrightarrow {S_{1}S_{2}}}$ . Speciellt om $k_{1}=k_{2}=-1$ ( punktreflektioner ) .

Härledning:

För kompositionen $\sigma _{2}\sigma _{1}$ av de två homoteterna $\sigma _{1},\sigma _{2}$ med centrerar $S_{1},S_{2}$ med

$\sigma _{1}:\mathbf {x} \to \mathbf {s} _{1}+k_{1}(\ mathbf {x} -\mathbf {s} _{1}),$

$\sigma _{2}:\mathbf {x} \to \mathbf {s} _{2}+k_{2}(\mathbf {x} -\mathbf {s} _{2})\$

man får genom beräkning för bilden av punkt $X:\mathbf {x}$ :

$(\sigma _{2}\sigma _{1})(\ mathbf {x} )=\mathbf {s} _{2}+k_{2}{\big (}\mathbf {s} _{1}+k_{1}(\mathbf {x} -\mathbf {s } _{1})-\mathbf {s} _{2}{\big )}$

${\ displaystyle \qquad \qquad \ =(1-k_{1})k_{2}\mathbf {s} _{1}+(1-k_{2})\mathbf {s} _{2}+k_{1 }k_{2}\mathbf {x} }$ .

Därför är sammansättningen

i fallet $k_{1}k_{2}=1$ en översättning i riktning ${\overrightarrow {S_{1}S_{2}}}$ med vektor $\ (1-k_{2})(\mathbf {s} _{2}-\mathbf {s} _{1})$ .

i fallet $k_{1}k_{2}\neq 1$ punkt

$S_{3}:\mathbf {s} _{3}={\frac {( 1-k_{1})k_{2}\mathbf {s} _{1}+(1-k_{2})\mathbf {s} _{2}}{1-k_{1}k_{2} }}=\mathbf {s} _{1}+{\frac {1-k_{2}}{1-k_{1}k_{2}}}(\mathbf {s} _{2}-\mathbf {s} _{1})$

är en fixpunkt (flyttas inte) och kompositionen

$\sigma _{2}\sigma _{1}:\ \mathbf {x} \to \mathbf {s} _ {3}+k_{1}k_{2}(\mathbf {x} -\mathbf {s} _{3})\quad$ .

är en homotet med mitten $S_{3}$ och förhållandet $k_{1}k_{2}$ . $S_{3}$ ligger på linjen ${\overline {S_{1}S_{2}}}$ .

Komposition med översättning

• Sammansättningen av en homoteti och en översättning är en homoteti.

Härledning:

Homotetins sammansättning

$\sigma :\mathbf {x} \to \mathbf {s} +k(\mathbf {x} -\mathbf {s} ) ,\;k\neq 1,\;$ och översättningen

$\tau :\mathbf {x} \to \mathbf {x} +\mathbf {v}$ är

$\tau \sigma :\mathbf {x} \to \mathbf {s} +\mathbf {v} +k(\mathbf {x} -\mathbf { s} )$

$=\mathbf {s} +{\frac {\mathbf {v} }{1-k} }+k\left(\mathbf {x} -(\mathbf {s} +{\frac {\mathbf {v} }{1-k}})\right)$

som är en homotet med centrum ${\displaystyle \mathbf {s} '=\mathbf {s} +{\frac {\mathbf {v} }{1-k}}} och$ förhållande $k$ .

I homogena koordinater

Homoteten $\sigma :\mathbf {x} \to \mathbf {s} +k(\mathbf {x} -\mathbf {s} )$ med centrum $S=(u,v)$ kan skrivas som kompositionen av en homoteti med mitten $O$ och en översättning:

$\mathbf {x} \to k\mathbf {x} +(1-k)\mathbf {s}$ .

Därför kan $\sigma$ representeras i homogena koordinater av matrisen:

${\begin{pmatrix}k&0&(1-k)u\\0&k&(1-k)v\\0&0&1\end{pmatrix} }$ .

Se även

• Skalning (geometri) en liknande uppfattning i vektorrum
• Homothetic center , centrum för en homothetic transformation som tar den ena av ett par former till den andra
• Hadwiger -förmodan om antalet strikt mindre homotetiska kopior av en konvex kropp som kan behövas för att täcka den
• Homotetisk funktion (ekonomi) , en funktion av formen f ( U ( y )) där U är en homogen funktion och f är en monotont ökande funktion .

Anteckningar

• HSM Coxeter, "Introduktion till geometri", Wiley (1961), sid. 94
• Hadamard, J. , Lektioner i plangeometri
• Meserve, Bruce E. (1955), "Homothetic transformations", Fundamental Concepts of Geometry , Addison-Wesley , s. 166–169
• Tuller, Annita (1967), A Modern Introduction to Geometries , University Series in Undergraduate Mathematics, Princeton, NJ: D. Van Nostrand Co.

externa länkar

• Homothety , interaktiv applet från Cut-the-Knot .