Simson linje

Simsonlinjen LN (röd) i triangeln ABC med avseende på punkt P på den omslutna cirkeln

I geometri , givet en triangel ABC och en punkt P på dess omkrets , är de tre punkterna närmast P på linjerna AB , AC och BC kolinjära . Linjen genom dessa punkter är Simson-linjen av P , uppkallad efter Robert Simson . Konceptet publicerades dock först av William Wallace 1799.

Det omvända är också sant; om de tre närmaste punkterna P på tre linjer är kolinjära, och inga två av linjerna är parallella, så ligger P på omkretsen av triangeln som bildas av de tre linjerna. Eller med andra ord, Simson-linjen för en triangel ABC och en punkt P är bara pedaltriangeln av ABC och P som har degenererats till en rät linje och detta tillstånd begränsar lokuset för P att spåra triangelns ABC omringade cirkel .

Ekvation

Placera triangeln i det komplexa planet, låt triangeln ABC med enhetsomkretscirkel ha hörn vars lägen har komplexa koordinater a , b , c , och låt P med komplexa koordinater p vara en punkt på den omslutna cirkeln. Simson-linjen är uppsättningen av punkter z som uppfyller

$2abc{\bar {z} }-2pz+p^{2}+(a+b+c)p-(bc+ca+ab)-{\frac {abc}{p}}=0,$

där en överstreck indikerar komplex konjugation .

Egenskaper

Simson-linjer (i rött) är tangenter till Steiner- deltoiden (i blått).

• Simson-linjen för en vertex i triangeln är höjden på triangeln som faller från den vertex, och Simson-linjen för punkten diametralt motsatt till vertexen är den sida av triangeln som är motsatt den vertexen.
• Om P och Q är punkter på den omslutna cirkeln, så är vinkeln mellan Simson-linjerna i P och Q halva vinkeln för bågen PQ . I synnerhet, om punkterna är diametralt motsatta, är deras Simson-linjer vinkelräta och i detta fall ligger skärningspunkten mellan linjerna på niopunktscirkeln .
• Låter H beteckna ortocentrumet för triangeln ABC , halverar Simson-linjen i P segmentet PH i en punkt som ligger på niopunktscirkeln.
• Givet två trianglar med samma omsluten cirkel, är vinkeln mellan Simson-linjerna i en punkt P på den omslutna cirkeln för båda trianglarna inte beroende av P .
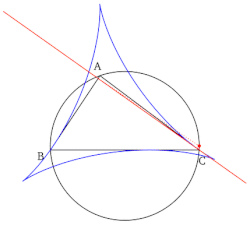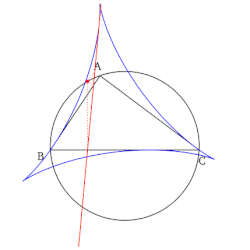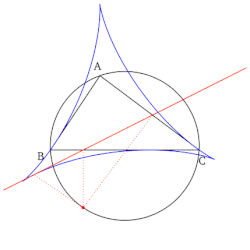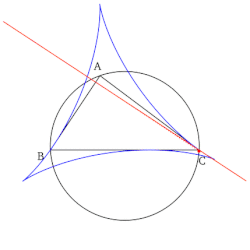
• Uppsättningen av alla Simson-linjer, när de är ritade, bildar ett kuvert i form av en deltoid känd som Steiner-deltoiden i referenstriangeln.
• Konstruktionen av Simson-linjen som sammanfaller med en sida av referenstriangeln (se första egenskapen ovan) ger en icke-trivial punkt på denna sidolinje. Denna punkt är reflektionen av foten av höjden (sänkt på sidolinjen) omkring mittpunkten av sidolinjen som konstrueras. Dessutom är denna punkt en tangentpunkt mellan sidan av referenstriangeln och dess Steiner-deltoid.
• En fyrhörning som inte är ett parallellogram har en och endast en pedalpunkt, kallad Simson-punkten, med avseende på vilken fötterna på fyrhörningen är kolinjära. Simson-punkten för en trapets är skärningspunkten mellan de två icke-parallella sidorna.
• Ingen konvex polygon med minst 5 sidor har en Simson-linje.

Bevis på existens

Bevismetoden är att visa att $\angle NMP+\angle PML=180^{\circ }$ . $PCAB$ är en cyklisk fyrhörning, så $\angle PBA+\angle ACP=\angle PBN+ \angle ACP=180^{\circ }$ . $PMNB$ är en cyklisk fyrhörning ( Thales sats ), så $\angle PBN+\angle NMP=180^{\circ }$ . Därför $\angle NMP=\angle ACP$ . Nu $PLCM$ cyklisk, så $vinkel ACP}$${\displaystyle \angle PML=\angle PCL=180^{\circ }-$ . Därför $\angle NMP+\angle PML=\angle ACP+(180^{\circ }-\ vinkel ACP)=180^{\cirkel }$ .

Generaliseringar

Generalisering 1

Projektionerna av Ap, Bp, Cp på BC, CA, AB är tre kolinjära punkter

• ₀₀₀₀₀₀ Låt ABC vara en triangel, låt en linje ℓ gå genom omkretscentrum O och låt en punkt P ligga på den omslutna cirkeln. Låt AP, BP, CP Cp _. Ap _, Bp _mötas ℓ vid respektive Låt A , B , C vara projektionerna av Ap , B _{p ,} C _p på BC, CA, AB respektive. Då A , B , C kolinjära. Dessutom passerar den nya linjen genom mittpunkten av PH , där H är ortocentrum för Δ ABC . Om ℓ passerar genom P , sammanfaller linjen med Simson-linjen.

En projektiv version av en Simson-linje

Generalisering 2

• Låt triangelns ABC hörn ligga på den koniska Γ, och låt Q, P vara två punkter i planet. Låt PA, PB, PC skära könen vid A ₁ , B ₁ , C ₁ respektive. QA1 skär BC vid A2 , QB1 skär _AC vid B2 _och QC1 _skär AB vid C2 _. _ _{_} _ _ _{_} _ Då är de fyra punkterna A ₂ , B ₂ , C ₂ och P kolinjära om bara Q ligger på den koniska Γ.

Generalisering 3

• RF Cyster generaliserade satsen till cykliska fyrhörningar i The Simson Lines of a Cyclic Quadrilateral

Se även

• Pedaltriangel
• Robert Simson

externa länkar

• Simson Line på cut-the-knot .org
• FM Jackson och Weisstein, Eric W. "Simson Line" . MathWorld .
• En generalisering av Neubergs teorem och Simson-Wallace-linjen vid Dynamic Geometry Sketches , en interaktiv dynamisk geometriskiss.