Centrallinje (geometri)

Inom geometrin är centrallinjer vissa speciella räta linjer som ligger i en triangels plan . Den speciella egenskap som särskiljer en rät linje som en central linje manifesteras via linjens ekvation i trilinjära koordinater . Denna speciella egenskap är också relaterad till begreppet triangelcentrum . Konceptet med en central linje introducerades av Clark Kimberling i en tidning som publicerades 1994.

Definition

Låt $ABC$ vara en plan triangel och låt $(x:y:z)$ vara de trilinjära koordinaterna för en godtycklig punkt i triangelplanet $ABC$ .

$ABC-$ plan vars ekvation i trilinjära koordinater har formen

f(a,b,c)x+g(a,b,c )y+h(a,b,c)z=0

där punkten med trilinjära koordinater $(f(a,b,c):g(a) ,b,c):h(a,b,c))$ är ett triangelcentrum, är en central linje i triangelns $ABC -plan$ relativt triangeln $ABC$ .

Centrallinjer som trilinjära polarer

Det geometriska förhållandet mellan en central linje och dess tillhörande triangelcentrum kan uttryckas med hjälp av begreppen trilinjära polärer och isogonala konjugat .

Låt X = ( u ( a , b , c ) : v ( a , b , c ) : w ( a , b , c ) ) vara ett triangelcentrum. Linjen vars ekvation är

x / u ( a , b , c ) + y / v ( a , b , c ) y + z / w ( a , b , c ) = 0

är den trilinjära polen av triangelns centrum X . Även punkten Y = ( 1 / u ( a , b , c ) : 1 / v ( a , b , c ) : 1 / w ( a , b , c ) ) är det isogonala konjugatet av triangelns centrum X .

Alltså den centrala linjen som ges av ekvationen

f ( a , b , c ) x + g ( a , b , c ) y + h ( a , b , c ) z = 0

är den trilinjära polären av det isogonala konjugatet av triangelns centrum ( f ( a , b , c ): g ( a , b , c ): h ( a , b , c )).

Byggande av centrala linjer

Låt X vara valfri triangelcentrum i triangeln ABC .

Rita linjerna AX , BX och CX och deras reflektioner i de inre bisektorerna av vinklarna vid hörnen A , B , C respektive.
De reflekterade linjerna är samtidiga och punkten för samtidighet är det isogonala konjugatet Y av X .
Låt cevianerna AY , BY , CY möta de motsatta sidlinjerna av triangeln ABC vid A' , B' , C' respektive. Triangeln A ' B ' C ' är den cevianska triangeln för Y.
Triangeln ABC och den cevianska triangeln A ' B ' C ' är i perspektiv och låter DEF vara perspektivaxeln för de två trianglarna. Linjen DEF är den trilinjära polära punkten Y . Linjen DEF är den centrala linjen associerad med triangelns centrum X .

Några namngivna centrallinjer

Låt Xn vara det _n : te triangelcentrumet i Clark Kimberlings Encyclopedia of Triangle Centers . Den Ln _centrala linjen associerad med Xn betecknas med _. Några av de namngivna centrallinjerna ges nedan.

Antiortisk axel som perspektivaxeln för triangeln ABC och dess excentrala triangel.

Centrallinje associerad med X ₁ , mitten: Antiortisk axel

Den centrala linjen associerad med mitten X ₁ = ( 1 : 1 : 1 ) (även betecknad med I ) är

x + y + z = 0.

Denna linje är den antiortiska axeln för triangeln ABC .

Det isogonala konjugatet av mitten av en triangel ABC är själva mitten. Så den antiortiska axeln, som är den centrala linjen som är associerad med mitten, är perspektivaxeln för triangeln ABC och dess inre triangel (den cevianska triangeln i triangelns ABCs centrum ).
Den antiortiska axeln för triangeln ABC är perspektivaxeln för triangeln ABC och den excentrala triangeln I ₁ I ₂ I ₃ i triangeln ABC .
Triangeln vars sidlinjer externt tangerar triangelns ABC excirkel är triangelns ABC extangenstriangel . En triangel ABC och dess utvidgningstriangel är i perspektiv och perspektivaxeln är den antiortiska axeln för triangeln ABC .

Centrallinje associerad med X ₂ , tyngdpunkten: Lemoine-axeln

De trilinjära koordinaterna för tyngdpunkten X ₂ (även betecknad med G ) i triangeln ABC är ( 1 / a : 1 / b : 1 / c ). Så den centrala linjen associerad med tyngdpunkten är den linje vars trilinjära ekvation är

x / a + y / b + z / c = 0.

Denna linje är Lemoine-axeln , även kallad Lemoine-linjen , för triangel ABC .

Det isogonala konjugatet av tyngdpunkten X2 är symmedianpunkten X6 (även betecknad med K ₎ som har trilinjära koordinater ( a : b : c ) _. Så Lemoine-axeln i triangeln ABC är den trilinjära polen av triangelns ABCs symmedianpunkt .
Den tangentiella triangeln i triangeln ABC är triangeln T _A T _B T _C som bildas av tangenterna till den omslutna cirkeln av triangeln ABC vid dess hörn. Triangeln ABC och dess tangentiella triangel är i perspektiv och perspektivaxeln är Lemoine-axeln i triangeln ABC .

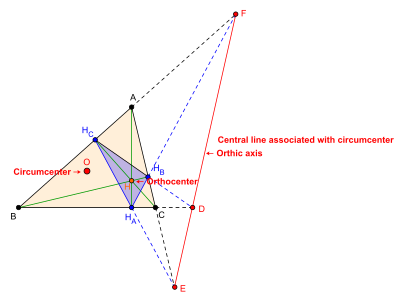
Centrallinje associerad med X ₃ , circumcenter: Orthic axel

De trilinjära koordinaterna för omkretscentrum X ₃ (även betecknad med O ) för triangeln ABC är ( cos A : cos B : cos C ). Så den centrala linjen associerad med circumcenter är den linje vars trilinjära ekvation är

x cos A + y cos B + z cos C = 0.

Denna linje är den ortiska axeln för triangeln ABC .

Det isogonala konjugatet av omkretscentrum X6 är ortocentrum X4 (även betecknat med H ) som har trilinjära koordinater (sek A :sek B : _sek C ) _. Så den ortiska axeln för triangeln ABC är den trilinjära polen för ortos centrum för triangeln ABC . Den ortiska axeln för triangeln ABC är perspektivaxeln för triangeln ABC och dess ortiska triangel H _A H _B H _C .

Centrallinje associerad med X4 _, ortocentret

De trilinjära koordinaterna för ortocentret X ₄ (även betecknat med H ) i triangeln ABC är (sek A : sek B : sek C ). Så den centrala linjen associerad med circumcenter är den linje vars trilinjära ekvation är

x sek A + y sek B + z sek C = 0.

Det isogonala konjugatet av en triangels ortocentrum är triangelns omkretscentrum. Så den centrala linjen som är associerad med ortocentret är den trilinjära polar av circumcenter.

Centrallinje associerad med X5 _, niopunktscentrumet

De trilinjära koordinaterna för det niopunktiga centrumet X ₅ (även betecknat med N ) i triangeln ABC är ( cos ( B − C ) : cos ( C − A ): cos ( A − B ) ). Så den centrala linjen som är associerad med niopunktscentrumet är den linje vars trilinjära ekvation är

x cos ( B − C ) + y cos ( C − A ) + z cos ( A − B ) = 0.

ABCs niopunktscentrum är Kosnitapunkten X ₅₄ i triangeln ABC . Så den centrala linjen som är förknippad med niopunktscentrumet är Kosnitapunktens trilinjära polar.
Kosnitapunkten är konstruerad enligt följande. Låt O vara omkretsen av triangeln ABC . Låt OA _, , O _B , O _C vara omkretsen av trianglarna BOC COA , AOB respektive . Linjerna AO _A , BO _B , CO _C är samtidiga och samtidighetspunkten är Kosnitapunkten i triangeln ABC . Namnet beror på J Rigby.

Centrallinje associerad med X ₆ , symmedianpunkten : Linje vid oändlighet

De trilinjära koordinaterna för symmedianpunkten X ₆ (även betecknad med K ) i triangeln ABC är ( a : b : c ). Så den centrala linjen som är associerad med symmedianpunkten är den linje vars trilinjära ekvation är

a x + b y + c z =0.

Denna linje är linjen i oändligheten i triangelns ABC- plan .
Det isogonala konjugatet av symmedianpunkten i triangeln ABC är tyngdpunkten för triangeln ABC . Följaktligen är den centrala linjen associerad med symmedianpunkten den trilinjära polära tyngdpunkten. Detta är perspektivaxeln för triangeln ABC och dess mediala triangel .

Några mer namngivna centrallinjer

Euler linje

Euler-linjen i triangeln ABC är den linje som går genom tyngdpunkten, circumcenter, ortocenter och niopunktscentrum i triangeln ABC . Eulerlinjens trilinjära ekvation är

x sin 2 A sin ( B − C ) + y sin 2 B sin ( C − A ) + z sin 2 C sin ( C − A ) = 0.

Detta är den centrala linjen som hör samman med triangelns centrum X ₆₄₇ .

Nagel linje

Nagel-linjen i triangeln ABC är den linje som går genom tyngdpunkten, mitten, Spiekers centrum och Nagel-punkten i triangeln ABC . Den trilinjära ekvationen för Nagel-linjen är

x a ( b − c ) + y b ( c − a ) + z c ( a − b ) = 0.

Detta är den centrala linjen som är associerad med triangelns centrum X ₆₄₉ .

Brocard axel

Brocard-axeln för triangeln ABC är linjen genom circumcenter och symmedianpunkten för triangeln ABC . Dess trilinjära ekvation är

x sin ( B − C ) + y sin ( C − A ) + z sin ( A − B ) = 0.

Detta är den centrala linjen associerad med triangelns centrum X ₅₂₃ .

Se även