Kiral polytop
Inom matematiken finns det två konkurrerande definitioner för en kiral polytop . En är att det är en polytop som är kiral (eller "enantiomorf"), vilket betyder att den inte har spegelsymmetri . Enligt denna definition skulle en polytop som inte alls saknar symmetri vara ett exempel på en kiral polytop.
Den andra, konkurrerande definitionen av en kiral polytop är att det är en polytop som är så symmetrisk som möjligt utan att vara spegelsymmetrisk, formaliserad i termer av verkan av polytopens symmetrigrupp på dess flaggor . Enligt denna definition är inte ens högsymmetriska och enantiomorfa polytoper såsom snubbkuben kirala. Mycket av studiet av symmetriska men kirala polytoper har utförts inom ramen för abstrakta polytoper , på grund av bristen på geometriska exempel.
Polytoper utan spegelsymmetri


|
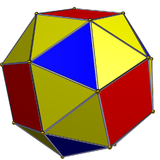
|
| Snubbkuben , vertextransitiv men inte spegelsymmetrisk . | |
Många polytoper saknar spegelsymmetri och bildar i den meningen kirala polytoper. Det enklaste exemplet är en skalentriangel .
Det är möjligt för polytoper att ha en hög grad av symmetri, men ändå sakna spegelsymmetri; ett enkelt exempel är disfenoiden när dess ytor inte är kongruenta med en likbent triangel ; ett annat exempel är snubkuben , som är vertextransitiv och kiral i denna mening.
Symmetriska kirala polytoper
Definition
Den mer tekniska definitionen av en kiral polytop är en polytop som har två banor av flaggor under sin grupp av symmetrier , med intilliggande flaggor i olika banor. Detta innebär att det måste vara vertex-transitive , edge-transitive , och face-transitive , eftersom varje vertex, kant eller yta måste representeras av flaggor i båda banorna; den kan dock inte vara spegelsymmetrisk, eftersom varje spegelsymmetri av polytopen skulle byta ut ett par intilliggande flaggor.
För ändamålen med denna definition kan symmetrigruppen för en polytop definieras på något av två olika sätt: den kan hänvisa till symmetrierna för en polytop som ett geometriskt objekt (i vilket fall polytopen kallas geometriskt kiral ) eller så kan den hänvisa till polytopens symmetri som en kombinatorisk struktur (en abstrakt polytop ). Kiralitet är meningsfullt för båda typerna av symmetri men de två definitionerna klassificerar olika polytoper som kirala eller icke-kirala.
I tre dimensioner
I tre dimensioner är det inte möjligt för en geometriskt kiral polytop att ha ändligt många ändliga ytor. Till exempel är snubbningskuben vertextransitiv, men dess flaggor har mer än två banor, och den är varken kanttransitiv eller ansiktstransitiv, så den är inte tillräckligt symmetrisk för att uppfylla den formella definitionen av kiralitet. De kvasireguljära polyedrarna och deras dualer, såsom kuboktaedern och den rombiska dodekaedern , ger en annan intressant typ av nästan-miss: de har två banor av flaggor, men är spegelsymmetriska, och inte alla intilliggande flaggpar tillhör olika banor. Men trots att ändliga kirala tredimensionella polyedrar inte finns, finns det oändliga tredimensionella kirala snedställda polyedrar av typerna {4,6}, {6,4} och {6,6}.
Vidare läsning
- Monson, Barry; Pisanski, Tomaž ; Schulte, Egon; Weiss, Asia Ivić (2007), "Semisymmetric graphs from polytopes", Journal of Combinatorial Theory , Series A, 114 (3): 421–435, arXiv : math/0606469 , doi : 10.1016/j.jcta.6006. , 60006 . MR 2310743 , S2CID 10203794 .
- Hubard, Isabel; Weiss, Asia Ivić (2005), "Self-duality of chiral polytopes", Journal of Combinatorial Theory , Series A, 111 (1): 128–136, doi : 10.1016/j.jcta.2004.11.012 , MR 214488 .
- Conder, Marston ; Hubard, Isabel; Pisanski, Tomaž (2008), "Constructions for chiral polytopes", Journal of the London Mathematical Society , Second Series, 77 (1): 115–129, doi : 10.1112/jlms/jdm093 , MR 2389920 .
- Monson, Barry; Ivić Weiss, Asia (2008), "Cayley-grafer och symmetriska 4-polytoper" , Ars Mathematica Contemporanea , 1 (2): 185–205, doi : 10.26493/1855-3974.79.919 , 61924 6 .