Symmetriskt minskande omarrangemang

I matematik är den symmetriska minskande omarrangemanget av en funktion en funktion som är symmetrisk och minskande, och vars nivåuppsättningar är av samma storlek som den ursprungliga funktionen.

Definition för set

Givet en mätbar mängd , $A,$ i $\mathbb {R} ^{n},$ definierar man den symmetriska omarrangeringen av $A,$ som kallas ${ \displaystyle A^{*},}$ som bollen centrerad vid origo, vars volym ( Lebesgue-mått ) är densamma som mängden $A.$

En motsvarande definition är

$$A^{*}=\left\{x\in \mathbb {R} ^{n}:\,\omega _{n}\cdot |x|^{n}<|A|\ höger\},$$

där $\omega _{n}$ är volymen för enhetsbollen och där $|A|$ är volymen av $A.$

Definition för funktioner

Omarrangemanget av en icke-negativ, mätbar funktion med verkligt värde $f$ vars nivå sätter $f^{-1}(y)$ (för $y\in \mathbb {R} _{\geq 0}$ ) har ändligt mått är

$$f^{*}(x)=\int _{0}^{\infty }\ mathbb {I} _{\{y:f(y)>t\}^{*}}(x)\,dt,$$

där $\mathbb {I} _{A}$ anger indikatorfunktionen för mängden $A.$ I ord ger värdet av $f^{*}(x)$ höjden $t$ för vilken radien för den symmetriska omarrangemanget av $\{y:f(y)>t\}$ är lika med $x.$ Vi har följande motiv för denna definition. Eftersom identiteten

$$g(x)=\int _{0}^{\infty }\mathbb {I} _{ \{y:g(y)>t\}}(x)\,dt,$$

gäller för alla icke-negativa funktioner $g,$ ovanstående definition är den unika definitionen som tvingar fram identiteten $\mathbb {I} _{A}^{*}= \mathbb {I} _{A^{*}}$ att hålla.

Egenskaper

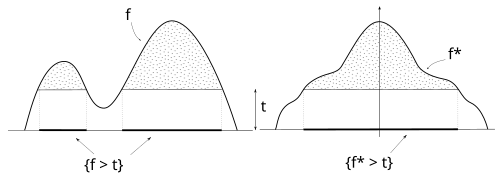
Funktionen och dess symmetriska minskande omarrangering bevarar måttet på nivåuppsättningar.

Funktionen $f^{*}$ är en symmetrisk och minskande funktion vars nivåmängder har samma mått som nivåmängderna för $f,$ dvs.

$$|\{x:f^{*}(x)>t\}|=|\{x:f(x)>t\}|.$$

Om $f$ är en funktion i $L^{p},$ så

$$\|f\|_{L^{p}}=\|f^{*}\|_{L^{p}}.$$

Hardy –Littlewood ojämlikheten gäller, det vill säga

$$\int fg\leq \int f^{*}g^{*}.$$

Vidare gäller ojämlikheten mellan Pólya och Szegő . Detta säger att om $1\leq p<\infty$ och om $f\in W^{1,p}$ så

$$\|\nabla f^{*}\|_{p}\leq \|\nabla f\|_{p}.$$

Den symmetriska minskande omordningen bevarar ordningen och minskar $L^{p}$ avstånd, det vill säga,

$$f\leq g{\text{ antyder }}f^{*}\leq g^{*}$$

och

$$\|fg\|_{L^{p}}\geq \|f^{*}-g^{*}\|_{L^{p}}.$$

Ansökningar

Pólya–Szegő-olikheten ger, i gränsfallet, med $p=1,$ den isoperimetriska olikheten . Man kan också använda vissa relationer med harmoniska funktioner för att bevisa Rayleigh-Faber-Krahn-olikheten .

Icke-symmetriskt minskande omarrangemang

Vi kan också definiera $f^{*}$ som en funktion på de icke-negativa reella talen snarare än på alla $\mathbb {R} ^{n}.$ Låt $(E,\mu )$ vara ett σ-ändligt måttrum , och låt $f:E\to [-\infty ,\infty ]$ vara en mätbar funktion som endast tar ändliga (det vill säga verkliga) värden μ-ae (där " $\mu$ -ae" betyder förutom möjligen på en uppsättning av $\mu$ -mått noll). Vi definierar fördelningsfunktionen μ $\displaystyle \mu _{f}:[0,\infty ]\to [0,\infty ]}$ med regeln

$$\mu _{f}(s)=\mu \{x\in E:\vert f(x)\vert >s\}.$$

Vi kan nu definiera den minskande omarrangeringen (eller ibland icke-ökande omarrangemang ) av $f$ som funktionen $f^{*}:[0,\ infty )\till [0,\infty ]$ av regeln

$$f^{*}(t)=\inf\{s\in [0,\infty ]:\mu _{f}(s)\leq t\}.$$

Observera att denna version av den minskande omarrangemanget inte är symmetrisk, eftersom den bara definieras på de icke-negativa reella talen. Men den ärver många av samma egenskaper som anges ovan som den symmetriska versionen, nämligen:

• $f$ och $f^{*}$ är likvärdiga , det vill säga de har samma fördelningsfunktion.
• Hardy-Littlewood-ojämlikheten gäller, det vill säga $\int _{E}|fg|\;d\mu \leq \int _{0}^{\infty }f^{*}(t)g^{*}(t)\;dt.$
• $\vert f\vert \leq \vert g\vert$$\mu$ -ae innebär $f^{*}\leq g^{*}.$
• $(af)^{*}=|a|f^{*}$ för alla reella tal $a.$
• $(f+g)^{*}(t_{1}+t_{2}) \leq f^{*}(t_{1})+g^{*}(t_{2})$ för alla $t_{1},t_{2}\in [0,\infty ).$
• $|f_{n}|\uparrow |f|$$\mu$ -ae innebär $f_{n}^{*}\uparrow f^{*}.$
• ${\displaystyle \left(\vert f\vert ^{p}\right)^{*}=(f^{*})^{p}} för$ alla positiva reella tal $sid.$
• $\|f\|_{L_{p}(E)}=\|f^{*}\|_{L_ {p}[0,\infty )}$ för alla positiva reella tal $sid.$
• $\|f\|_{L_{\infty }(E)}=f^{*}(0).$

Den (icke-symmetriska) minskande omarrangemangsfunktionen uppstår ofta i teorin om omarrangeringsinvarianta Banachfunktionsrum. Särskilt viktigt är följande:

Luxemburgs representationsteorem. Låt ${\displaystyle \rho } vara en omarrangemangs-$$(E,\mu ).$ Banach-funktionsnorm över ett resonansmåttutrymme Då finns det en (möjligen inte unik) omarrangerings-invariant funktionsnorm ${\overline {\rho }}$ på $[0, \infty )$ så att $\rho (f)={\overline {\rho }}(f^{*})$ för alla icke-negativa mätbara funktioner $f:E\ till [0,\infty ]$ som har ändligt värde $\mu$ -ae

Observera att definitionerna av all terminologi i ovanstående sats (det vill säga Banach-funktionsnormer, omarrangemangsinvarianta Banach-funktionsutrymmen och resonantmåttsutrymmen) finns i avsnitt 1 och 2 i Bennett och Sharpleys bok (jfr referenserna Nedan).

Se även

• Isoperimetrisk olikhet – Geometrisk olikhet som sätter en nedre gräns för ytan av en mängd givet dess volym
• Skiktårta representation
• Rayleigh–Faber–Krahn ojämlikhet
• Riesz omarrangemang ojämlikhet
• Sobolev space – Vektorrum av funktioner i matematik
• Szegő ojämlikhet