Funktionssammansättning

I matematik är funktionssammansättning en operation $\circ$ som tar två funktioner $f$ och $g$ , och producerar en funktion $h = g \circ f$ så att $h (x) = (f (x))$ g . I denna operation appliceras funktionen $g$ på resultatet av applicering av funktionen $f$ till $x$ . Det vill säga funktionerna $f : X \to Y$ och $g : Y \to Z$ är sammansatta för att ge en funktion som mappar $x$ i domän $X$ till $g (f (x))$ i kodomän $Z$ . Intuitivt, om $z$ är en funktion av $y$ och $y$ är en funktion av $x$ , så är $z$ en funktion av $x$ . Den resulterande sammansatta funktionen betecknas $g \circ f : X \to Z$ , definierad av $(g \circ f)(x) = g (f (x))$ för alla $x$ i $X$ .

Notationen $g \circ f$ läses som " $g$ av $f$ ", " $g$ efter $f$ ", " $g$ cirkel $f$ ", " $g$ rund $f$ ", " $g$ om $f$ ", " $g$ sammansatt med $f$ ", " $g$ efter $f$ " , " $f$ sedan $g$ ", eller " $g$ på $f$ " eller " sammansättningen av $g$ och $f$ ". Intuitivt är att komponera funktioner en kedjeprocess där utdata från funktion $f$ matar ingången för funktion $g$ .

Sammansättningen av funktioner är ett specialfall av sammansättningen av relationer , ibland också betecknat med $\circ$ . Som ett resultat är alla egenskaper hos sammansättning av relationer sanna för sammansättning av funktioner, såsom egenskapen associativitet .

Sammansättning av funktioner skiljer sig från multiplikation av funktioner (om de definieras alls), och har några helt olika egenskaper; i synnerhet är sammansättningen av funktioner inte kommutativ .

Exempel

Konkret exempel på sammansättningen av två funktioner.

Sammansättning av funktioner på en ändlig mängd: Om $f = {(1, 1), (2, 3), (3, 1), (4, 2)}$ och $g = {(1, 2), (2, 3), (3, 1), (4, 2)}$ , sedan $g \circ f = {(1, 2), (2, 1), (3, 2), (4, 3)} ,$ som visas i figuren.
Sammansättning av funktioner på en oändlig mängd : Om $f : R \to R$ (där $R$ är mängden av alla reella tal ) ges av $f (x) = 2 x + 4$ och $g : R \to R$ ges av $g (x) = x 3$ , sedan:
$(f \circ g)(x) = f (g (x)) = f (x 3) = 2 x 3 + 4$ , och

$(g \circ f)(x) = g (f (x)) = g (2 x + 4) = (2 x + 4) 3$ .
Om ett flygplans höjd vid tidpunkten $t x (p\circa)(t)$ $är$ a $(t) och$ lufttrycket på höjden $är$ p $(x),$ så är trycket runt planet vid tidpunkten $t$ .

Egenskaper

Sammansättningen av funktioner är alltid associativ — en egenskap som ärvs från sammansättningen av relationer . Det vill säga om $f$ , $g$ och $h$ är komponerbara så är $f \circ (g \circ h) = (f \circ g) \circ h$ . Eftersom parenteserna inte ändrar resultatet utelämnas de i allmänhet.

I strikt mening är sammansättningen $g \circ f$ endast meningsfull om samdomänen för $f$ är lika med domänen för $g$ ; i en vidare mening är det tillräckligt att den förra är en otillbörlig delmängd av den senare. Dessutom är det ofta bekvämt att tyst begränsa domänen för $f$ , så att $f$ endast producerar värden i domänen för $g$ . Till exempel sammansättningen $g \circ f$ för funktionerna $f : R \to (-\infty,+9]$ definierade av $f (x) = 9 - x 2$ och $g : [0,+\infty) \to R$ definierade av $g(x)={\sqrt {x}}$ kan definieras i intervallet $[-3,+3]$ .

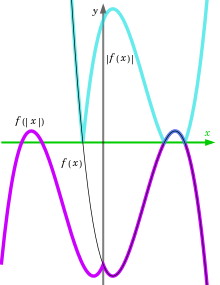
Sammansättningar av två reella funktioner, det absoluta värdet och en kubisk funktion , i olika ordningsföljder, visar en icke-kommutativitet av sammansättningen.

Funktionerna $g$ och $f$ sägs pendla med varandra om $g \circ f = f \circ g$ . Kommutativitet är en speciell egenskap, som endast uppnås genom särskilda funktioner, och ofta under speciella omständigheter. Till exempel $| x | + 3 = | x + 3 |$ endast när $x \geq 0$ . Bilden visar ett annat exempel.

Sammansättningen av en-till-en (injektiv) funktioner är alltid en-till-en. På samma sätt är sammansättningen av onto (surjektiva) funktioner alltid onto. Härav följer att sammansättningen av två bijektioner också är en bijektion. Den inversa funktionen av en komposition (antas inverterbar) har egenskapen att $(f \circ g) -1 = g -1 \circ f -1$ .

Derivat av sammansättningar som involverar differentierbara funktioner kan hittas med hjälp av kedjeregeln . Högre derivator av sådana funktioner ges av Faà di Brunos formel .

Sammansättning monoider

Antag att en har två (eller flera) funktioner $f : X \to X,$ $g : X \to X$ som har samma domän och kodomän; dessa kallas ofta transformationer . Då kan man bilda kedjor av transformationer sammansatta, såsom $f \circ f \circ g \circ f$ . Sådana kedjor har den algebraiska strukturen av en monoid , kallad en transformation monoid eller (mycket mer sällan) en sammansättning monoid . I allmänhet kan transformationsmonoider ha anmärkningsvärt komplicerad struktur. Ett särskilt anmärkningsvärt exempel är de Rham-kurvan . Uppsättningen av alla funktioner $f : X \to X$ kallas heltransformationssemigruppen eller symmetrisk halvgrupp på $X$ . (Man kan faktiskt definiera två semigrupper beroende på hur man definierar semigruppoperationen som vänster eller höger sammansättning av funktioner.)

Likheten som omvandlar triangeln EFA till triangeln ATB är sammansättningen av en homotet

H

och en rotation

R

, vars gemensamma centrum är S. Till exempel är bilden av A under rotationen

R

U , som kan skrivas

R

( A ) = U. Och

H

( U ) = B betyder att avbildningen

H

omvandlar U till B. Således

H (R

( A )) =

(H \circ R)

( A ) = B .

Om transformationerna är bijektiva (och därmed inverterbara), så bildar mängden av alla möjliga kombinationer av dessa funktioner en transformationsgrupp ; och en säger att gruppen genereras av dessa funktioner. Ett grundläggande resultat i gruppteorin, Cayleys teorem , säger i huvudsak att vilken grupp som helst är i själva verket bara en undergrupp av en permutationsgrupp (upp till isomorfism ).

Mängden av alla bijektiva funktioner $f : X \to X$ (kallade permutationer ) bildar en grupp med avseende på funktionssammansättning. Detta är den symmetriska gruppen , även ibland kallad kompositionsgruppen .

I den symmetriska halvgruppen (av alla transformationer) finner man också en svagare, icke-unik föreställning om invers (kallad pseudoinvers) eftersom den symmetriska halvgruppen är en vanlig halvgrupp .

Funktionella krafter

Om $Y \subseteq X$ , då kan $f : X \to Y$ komponera med sig själv; detta betecknas ibland som $f 2$ . Det är:

(f \circ f)(x) = f (f (x)) = f 2 (x)

(f \circ f \circ f)(x) = f (f (f (x))) = f 3 (x)

(f \circ f \circ f \circ f)(x) = f (f (f (f (x)))) = f 4 (x)

Mer generellt, för vilket naturligt tal $n \geq 2 som helst$ , kan den $n:$ te funktionella potensen definieras induktivt av $f n = f \circ f n -1 = f n -1 \circ f$ , en notation introducerad av Hans Heinrich Bürmann ^{[ citat behövs ]} och John Frederick William Herschel . Upprepad sammansättning av en sådan funktion med sig själv kallas itererad funktion .

Enligt konventionen definieras $f 0$ som identitetskartan på $fs$ domän, $id X$ .
Om även $Y = X$ och $f : X \to X$ medger en invers funktion $f -1 ,$ definieras negativa funktionella potenser $f - n för$ $n > 0$ som den negerade potensen av den inversa funktionen: $f - n = (f -1) n$ .

Notera: Om $f$ tar sina värden i en ring (särskilt för reellt eller komplext värderat $f$ ), finns det en risk för förvirring, eftersom $f n$ också kan stå för den $n$ -faldiga produkten av $f$ , t.ex. $f 2 (x) = f (x) \cdot f (x)$ . För trigonometriska funktioner avses vanligtvis det senare, åtminstone för positiva exponenter. Till exempel, i trigonometri representerar denna upphöjda notation standardexponentiering när den används med trigonometriska funktioner : $sin 2 (x) = sin(x) \cdot sin(x)$ . Men för negativa exponenter (särskilt −1) hänvisar det ändå vanligtvis till den inversa funktionen, t.ex. $tan -1 = arctan \neq 1/tan$ .

I vissa fall, när, för en given funktion $f$ , ekvationen $g \circ g = f$ har en unik lösning $g$ , kan den funktionen definieras som den funktionella kvadratroten ur $f$ , och sedan skrivas som $g = f 1/2$ .

Mer generellt, när $g n = f$ har en unik lösning för något naturligt tal $n > 0$ , då kan $f m / n$ definieras som $g m$ .

Under ytterligare begränsningar kan denna idé generaliseras så att iterationsantalet blir en kontinuerlig parameter; i detta fall kallas ett sådant system ett flöde , specificerat genom lösningar av Schröders ekvation . Itererade funktioner och flöden förekommer naturligt i studiet av fraktaler och dynamiska system .

För att undvika tvetydighet väljer vissa matematiker ^{[ citat behövs ]} att använda $\circ$ för att beteckna den sammansättningsmässiga betydelsen, och skriver $f \circ n (x)$ för $n$ -te iteraten av funktionen $f (x)$ , som i till exempel $f \circ3 (x)$ betyder $f (f (f (x)))$ . För samma ändamål användes $f [n] (x) av$ Benjamin Peirce medan Alfred Pringsheim och Jules Molk föreslog $n f (x)$ istället.

Alternativa beteckningar

Många matematiker, särskilt inom gruppteori , utelämnar sammansättningssymbolen och skriver $gf$ för $g \circ f$ .

I mitten av 1900-talet bestämde sig vissa matematiker för att det var för förvirrande att skriva " $g \circ f$ " till att betyda "först tillämpa $f$ , sedan $g " och de bestämde sig för att ändra notationer.$ De skriver " $xf$ " för " $f (x)$ " och " $(xf) g$ " för " $g (f (x) )$ ". Detta kan vara mer naturligt och verka enklare än att skriva funktioner till vänster i vissa områden – i linjär algebra, till exempel, när $x$ är en radvektor och $f$ och $g$ betecknar matriser och sammansättningen är genom matrismultiplikation . Denna alternativa notation kallas postfix-notation . Ordningen är viktig eftersom funktionssammansättningen inte nödvändigtvis är kommutativ (t.ex. matrismultiplikation). Successiva transformationer som appliceras och komponeras till höger överensstämmer med lässekvensen från vänster till höger.

Matematiker som använder postfix-notation kan skriva " $fg$ ", vilket betyder att först applicera $f$ och sedan applicera $g$ , i enlighet med den ordning symbolerna förekommer i postfix-notation, vilket gör notationen " $fg$ " tvetydig. Datavetare kan skriva " $f; g$ " för detta, och därigenom disambiguera ordningen på sammansättningen. För att skilja den vänstra kompositionsoperatorn från ett textsemikolon, i Z-notationen används tecknet ⨾ för vänsterrelationskomposition . Eftersom alla funktioner är binära relationer är det korrekt att använda semikolonet [fett] för funktionssammansättning också (se artikeln om sammansättning av relationer för ytterligare detaljer om denna notation).

Kompositionsoperatör

Givet en funktion $g$ definieras kompositionsoperatorn C g som den operator $som mappar$ funktioner till funktioner som

C_{g}f=f\circ g.

Kompositionsoperatorer studeras inom området operatorteori .

I programmeringsspråk

Funktionssammansättning visas i en eller annan form i många programmeringsspråk .

Multivariata funktioner

Partiell sammansättning är möjlig för multivariata funktioner . Funktionen som uppstår när något argument $x i$ för funktionen $f$ ersätts med funktionen $g$ kallas en sammansättning av $f$ och $g$ i vissa datortekniska sammanhang och betecknas $f | x i = g$

f|_{x_{i}=g}=f(x_{1},\ldots,x_{i-1},g(x_{1},x_{2},\ldots,x_{n }),x_{i+1},\ldots ,x_{n}).

När $g$ är en enkel konstant $b$ , urartar sammansättningen till en (partiell) värdering, vars resultat också kallas restriktion eller co-faktor .

f|_{x_{i}=b}=f(x_{1},\ldots,x_{i-1},b,x_{i+1},\ldots,x_{n}).

I allmänhet kan sammansättningen av multivariata funktioner involvera flera andra funktioner som argument, som i definitionen av primitiv rekursiv funktion . Givet $f$ , en $n$ -är funktion och $n$ $m$ -ära funktioner $g 1, ..., g n$ är sammansättningen av $f$ med $g 1, ... , g n$ den $m$ -ära funktionen

h(x_{1},\ldots ,x_{m})=f(g_{1}(x_{1},\ldots,x_{m}),\ldots ,g_{n}(x_{ 1},\ldots ,x_{m})).

Detta kallas ibland den generaliserade sammansättningen eller superpositionen av f med $g 1, ..., g n$ . Den partiella sammansättningen i endast ett argument som nämnts tidigare kan instansieras från detta mer allmänna schema genom att ställa in alla argumentfunktioner utom en för att vara lämpligt valda projektionsfunktioner . Här $g 1, ..., g n$ ses som en enkel vektor/ tupelvärderad funktion i detta generaliserade schema, i vilket fall detta är precis standarddefinitionen av funktionssammansättning.

En uppsättning finitära operationer på någon basuppsättning X kallas en klon om den innehåller alla projektioner och är stängd under generaliserad sammansättning. Observera att en klon i allmänhet innehåller operationer av olika arter . Begreppet kommutering finner också en intressant generalisering i det multivariata fallet; en funktion f av aritet n sägs pendla med en funktion g av aritet m om f är en homomorfism som bevarar g , och vice versa, dvs.

f(g(a_{11},\ldots,a_{1m}),\ldots ,g(a_{n1},\ldots,a_{nm}))=g(f(a_{11}, \ldots ,a_{n1}),\ldots ,f(a_{1m},\ldots ,a_{nm})).

En unär operation pendlar alltid med sig själv, men detta är inte nödvändigtvis fallet för en binär (eller högre aritets) operation. En binär (eller högre aritet) operation som pendlar med sig själv kallas medial eller entropisk .

Generaliseringar

Sammansättning kan generaliseras till godtyckliga binära relationer . Om $R \subseteq X \times Y$ och $S \subseteq Y \times Z$ är två binära relationer, så är deras sammansättning $R \circ S$ relationen definierad som ${(x, z) \in X \times Z : \exists y \in Y . (x, y) \in R \land (y, z) \in S}$ . Om man betraktar en funktion som ett specialfall av en binär relation (nämligen funktionella relationer ), uppfyller funktionssammansättning definitionen för relationssammansättning. En liten cirkel $R \circ S$ har använts för infixnotation av sammansättning av relationer, såväl som funktioner. När den används för att representera sammansättningen av funktioner ${\displaystyle (g\circ f)(x)\ =\ g(f(x))},$ men texten sekvensen är omvänd för att illustrera de olika operationssekvenserna i enlighet därmed.

Sammansättningen definieras på samma sätt för partiella funktioner och Cayleys teorem har sin analog som kallas Wagner–Prestons teorem .

Kategorin av mängder med funktioner som morfismer är den prototypiska kategorin . Axiomen för en kategori är i själva verket inspirerade av egenskaperna (och även definitionen) av funktionssammansättning. De strukturer som kompositionen ger är axiomatiserade och generaliserade i kategoriteorin med begreppet morfism som kategoriteoretisk ersättning av funktioner. Den omvända sammansättningsordningen i formeln $omvända . (f\circg) -1 =(g - 1\circf - 1)$ gäller för sammansättning av relationer med relationer , och alltså i gruppteorin Dessa strukturer bildar dolkkategorier .

Typografi

Kompositionssymbolen $\circ$ är kodad som U+2218 ∘ RING OPERATÖR ( &compfn;, &SmallCircle; ) ; se om gradsymboler för liknande Unicode-tecken. I TeX skrivs det \circ .

Se även

Spindelnätsplott – en grafisk teknik för funktionell komposition
Kombinationslogik
Kompositionsring , en formell axiomatisering av kompositionsoperationen
Flöde (matematik)
Funktionssammansättning (datavetenskap)
Funktion av stokastisk variabel , fördelning av en funktion av en stokastisk variabel
Funktionell nedbrytning
Funktionell kvadratrot
Funktion av högre ordning
Oändliga sammansättningar av analytiska funktioner
Itererad funktion
Lambdakalkyl

Anteckningar

externa länkar

"Composite function" , Encyclopedia of Mathematics , EMS Press , 2001 [1994]
" Composition of Functions " av Bruce Atwood, Wolfram Demonstrations Project , 2007.

Funktion
$x \mapsto f (x)$
Exempel på domäner och koddomäner
$X$ → $\mathbb {B}$ , $\mathbb {B}$ → $X$ , $\mathbb {B} ^{n}$ → $X$ $X$ → $\mathbb {Z}$ , $\mathbb {Z}$ → $X$ $X$ → $\mathbb {R}$ , $\mathbb {R}$ → $X$ , $\mathbb {R} ^{n}$ → $X$ $X$ → $\mathbb {C}$ , $\mathbb {C}$ → $X$ , $\mathbb {C} ^{n}$ → $X$
Klasser/fastigheter
Konstant Identitet Linjär Polynom Rationell Algebraisk Analytisk Slät Kontinuerlig Mätbar Injektiv Surjektiv Bijektiv
Konstruktioner
Restriktion Sammansättning λ Omvänd
Generaliseringar
Partiell Flervärdigt Implicit Plats