Gräns ​​(kategoriteori)

Inom kategoriteorin , en gren av matematiken , fångar det abstrakta begreppet en gräns de väsentliga egenskaperna hos universella konstruktioner såsom produkter , tillbakadragningar och omvända gränser . Den dubbla föreställningen om en colimit generaliserar konstruktioner som osammanhängande fackföreningar , direkta summor , biprodukter , pushouts och direkta gränser .

Gränser och kolimiter, liksom de starkt besläktade föreställningarna om universella egenskaper och adjoint funktorer , existerar på en hög abstraktionsnivå. För att förstå dem är det bra att först studera de specifika exempel som dessa begrepp är avsedda att generalisera.

Definition

Gränser och samgränser i en kategori $C$ definieras med hjälp av diagram i $C$ . Formellt är ett diagram av form $J$ i $C$ en funktion från $J$ till $C$ :

$F:J\to C.$

Kategorin $J$ är tänkt som en indexkategori och diagrammet $F$ är tänkt att indexera en samling objekt och morfismer i $C$ mönstrat på $J$ .

Man är oftast intresserad av fallet där kategorin $J$ är en liten eller till och med ändlig kategori. Ett diagram sägs vara litet eller ändligt närhelst $J$ är.

Gränser

Se även: Omvänd gräns

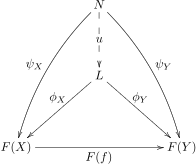
Låt $F:J\to C$ vara ett diagram av formen $J$ i en kategori $C$ . En kon till $F$ är ett objekt $N$ av $C$ tillsammans med en familj $\psi _{X}:N\ till F(X)$ av morfismer indexerade av objekten $X$ av $J$ , så att för varje morfism $f:X\to Y$ i ${\ displaystyle J}$ , vi har $F(f)\circ \psi _{X}=\psi _{Y}$ .

En gräns för diagrammet $F:J\to C$ är en kon $(L,\phi )$ till $F$ så att för varannan kon $(N,\psi )$ till $F$ det finns en unik morfism $u:N\to L$ så att $\phi _{X}\circ u=\psi _{X}$ för alla $X$ i $J$ .

Man säger att könen $(N,\psi )$ faktorer genom könen $(L,\phi )$ med den unika faktoriseringen $u$ . Morfismen $u$ kallas ibland den förmedlande morfismen .

Gränser kallas också universella koner , eftersom de kännetecknas av en universell egenskap (se nedan för mer information). Som med alla universella egenskaper, beskriver definitionen ovan ett balanserat tillstånd av generalitet: Limitobjektet $L$ måste vara tillräckligt generellt för att tillåta vilken annan kon att ta sig igenom det; å andra sidan $L$ vara tillräckligt specifik, så att endast en sådan faktorisering är möjlig för varje kon.

Gränser kan också karakteriseras som terminalobjekt i kategorin koner till F .

Det är möjligt att ett diagram inte har någon gräns alls. Men om ett diagram har en gräns är denna gräns i grunden unik: den är unik upp till en unik isomorfism . Av denna anledning talar man ofta om gränsen för F .

Colimits

Se även: Direkt gräns

De dubbla föreställningarna om gränser och koner är colimits och co-cones. Även om det är enkelt att erhålla definitionerna av dessa genom att invertera alla morfismer i ovanstående definitioner, kommer vi uttryckligen att ange dem här:

En samkon av ett diagram $F:J\to C$ är ett objekt $N$ av $C$ tillsammans med en familj av morfismer

$\psi _{X}:F(X)\to N$

för varje objekt $X$ av $J$ , så att för varje morfism $f:X\to Y$ i $J$ , har vi $\psi _{Y}\circ F(f)=\psi _{X}$ .

En colimit av ett diagram $F:J\to C$ är en co-kon $(L,\phi )$ av $F$ så att för någon annan co-kon $(N,\psi )$ av $F$ finns det en unik morfism $u:L\to N$ så att $u\circ \phi _{X}=\psi _{X}$ för alla $X$ i $J$ .

Colimits kallas också universella co-cones . De kan karakteriseras som initialobjekt i kategorin co-cones från $F$ .

Precis som med limits, om ett diagram $F$ har en colimit så är denna colimit unik upp till en unik isomorfism.

Variationer

Gränser och kogränser kan också definieras för samlingar av objekt och morfismer utan användning av diagram. Definitionerna är desamma (observera att i definitionerna ovan behövde vi aldrig använda sammansättning av morfismer i $J$ ). Denna variation tillför dock ingen ny information. Varje samling av objekt och morfismer definierar en (eventuellt stor) riktad graf $G$ . Om vi ​​låter $J$ vara den fria kategorin genererad av $G$ , finns det ett universellt diagram $F:J\to C$ vars bild innehåller $G$ . Gränsen (eller samgränsen) för detta diagram är densamma som gränsen (eller samgränsen) för den ursprungliga samlingen av föremål och morfismer.

Svag gräns och svag gräns definieras som gränser och gränser, förutom att unikhetsegenskapen för den förmedlande morfismen tas bort.

Exempel

Gränser

Definitionen av gränser är tillräckligt generell för att sammanfatta flera konstruktioner användbara i praktiska sammanhang. I det följande kommer vi att betrakta gränsen ( L , φ ) för ett diagram F : J → C .

• Terminalobjekt . Om J är den tomma kategorin finns det bara ett diagram av form J : det tomma (liknande den tomma funktionen i mängdteorin). En kon till det tomma diagrammet är i huvudsak bara ett objekt av C . Gränsen för F är vilket objekt som helst som unikt beaktas av alla andra objekt. Detta är bara definitionen av ett terminalobjekt .
• Produkter . Om J är en diskret kategori så är ett diagram F i huvudsak ingenting annat än en familj av objekt av C , indexerad med J . Gränsen L för F kallas produkten av dessa objekt. Könen φ består av en familj av morfismer φ _X : L → F ( X ) som kallas produktens projektioner . I kategorin uppsättningar , till exempel, ges produkterna av kartesiska produkter och projektionerna är bara de naturliga projektionerna på de olika faktorerna.
  • Krafter . Ett specialfall av en produkt är när diagrammet F är en konstant funktion för ett objekt X av C . Gränsen för detta diagram kallas den J ^:te potensen av X och betecknas X ^J .
• Equalizers . Om J är en kategori med två objekt och två parallella morfismer från ett objekt till det andra, så är ett diagram av form J ett par parallella morfismer i C . Gränsen L för ett sådant diagram kallas en utjämnare av dessa morfismer.
  • Kärnor . En kärna är ett specialfall av en equalizer där en av morfismerna är en nollmorfism .
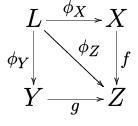
• Pullbacks . Låt F vara ett diagram som plockar ut tre objekt X , Y och Z i C , där de enda icke-identitetsmorfismerna är f : X → Z och g : Y → Z . Gränsen L för F kallas en pullback eller en fiberprodukt . Det kan fint visualiseras som en kommutativ kvadrat :

• Omvända gränser . Låt J vara en riktad mängd (betraktad som en liten kategori genom att lägga till pilar i → j om och endast om i ≥ j ) och låt F : J ^op → C vara ett diagram. Gränsen för F kallas (förvirrande nog) en omvänd gräns eller projektiv gräns .
• Om J = 1 , kategorin med ett enda objekt och morfism, så är ett diagram av form J i huvudsak bara ett objekt X av C . En kon till ett objekt X är bara en morfism med codomän X . En morfism f : Y → X är en gräns för diagrammet X om och endast om f är en isomorfism . Mer generellt, om J är vilken kategori som helst med ett initialt objekt i , så har varje diagram av form J en gräns, nämligen vilket objekt som helst som är isomorft till F ( i ). En sådan isomorfism bestämmer unikt en universell kon till F .
• Topologiska gränser . Funktionsgränser är ett specialfall av filtergränser , som är relaterade till kategoriska gränser enligt följande. Givet ett topologiskt utrymme X , beteckna med F uppsättningen filter på X , x ∈ X en punkt, V ( x ) ∈ F grannskapsfiltret för x , A ∈ F ett visst filter och $F_{x,A}=\{G\in F\mid V(x)\cup A\subset G\}$ uppsättningen filter som är finare än A och att konvergera till x . Filtren F ges en liten och tunn kategoristruktur genom att lägga till en pil A → B om och endast om A ⊆ B . Injektionen $I_{x,A}:F_{x,A}\to F$ blir en funktion och följande ekvivalens gäller:

x är en topologisk gräns för A om och endast om A är en kategorisk gräns för $I_{x,A}$

Colimits

Exempel på kogränser ges av de dubbla versionerna av exemplen ovan:

• Initiala objekt är kogränser av tomma diagram.
• Samprodukter är kolimiter av diagram indexerade efter diskreta kategorier.
  • Samkrafter är kogränser av konstantdiagram från diskreta kategorier.
• Coequalizers är kogränser för ett parallellt par av morfismer.
  • Kokärnor är samutjämnare av en morfism och en parallell nollmorfism.
• Pushhout är kogränser av ett par morfismer med gemensam domän.
• Direkta gränser är kogränser av diagram indexerade av riktade uppsättningar.

Egenskaper

Förekomsten av gränser

Ett givet diagram F : J → C kan ha eller inte ha en gräns (eller samgräns) i C . Faktum är att det kanske inte ens finns en kon till F , än mindre en universell kon.

En kategori C sägs ha gränser för form J om varje diagram av form J har en gräns i C . Specifikt sägs en kategori C

• har produkter om den har gränser för form J för varje liten diskret kategori J (den behöver inte ha stora produkter),
• har utjämnare om den har gränser för formen $\bullet \rightarrows \bullet$ (dvs varje parallell par av morfismer har en equalizer),
• har pullbacks om den har formgränser $\bullet \rightarrow \bullet \leftarrow \bullet$ (dvs varje par av morfismer med gemensamt kodomän har en pullback).

En komplett kategori är en kategori som har alla små gränser (dvs. alla gränser för form J för varje liten kategori J ).

Man kan också göra de dubbla definitionerna. En kategori har colimits av form J om varje diagram av form J har colimit i C . En cocomplete kategori är en som har alla små colimits.

Existenssatsen för gränser säger att om en kategori C har utjämnare och alla produkter indexerade av klasserna Ob( J ) och Hom( J ), så har C alla gränser för form J . I detta fall kan gränsen för ett diagram F : J → C konstrueras som utjämnaren för de två morfismerna

$s,t:\prod _{i\in \operatörsnamn { Ob} (J)}F(i)\rightrightarrows \prod _{f\in \operatörsnamn {Hom} (J)}F(\operatörsnamn {cod} (f))$

ges (i komponentform) av

${\begin{aligned}s&={\bigl (}F(f)\circ \pi _{\operatörsnamn {dom} (f)}{\bigr )}_{f\in \operatörsnamn {Hom} (J)}\\t&={\bigl (}\pi _{\operatörsnamn {cod} (f)}{\bigr )}_{f\in \operatörsnamn {Hom} (J)}.\end{aligned }}$

Det finns en dubbel existenssats för kogränser i termer av samutjämnare och samprodukter. Båda dessa satser ger tillräckliga och nödvändiga förutsättningar för existensen av alla (sam)gränser för form J .

Universell egendom

Limits och colimits är viktiga specialfall av universella konstruktioner .

Låt C vara en kategori och låt J vara en liten indexkategori. Funktionskategorin C ^J kan ses som kategorin för alla diagram av form J i C . Diagonalfunktionen _

$\Delta :{\mathcal {C}}\to {\mathcal {C}}^{\mathcal {J}}$

är den funktion som mappar varje objekt N i C till den konstanta funktorn Δ( N ) : J → C till N . Det vill säga, Δ( N )( X ) = N för varje objekt X i J och Δ( N )( f ) = id _N för varje morfism f i J.

Givet ett diagram F : J → C (tänkt som ett objekt i C ^J ), är en naturlig transformation ψ : Δ( N ) → F (som bara är en morfism i kategorin C ^J ) samma sak som en kon från N till F. _ För att se detta, notera först att Δ( N )( X ) = N för alla X innebär att komponenterna i ψ är morfismer ψ _X : N → F ( X ), som alla delar domänen N . Dessutom är kravet på att konens diagram pendlar sant helt enkelt för att denna ψ är en naturlig transformation. (Dubbelt sett är en naturlig transformation ψ : F → Δ( N ) samma sak som en medkon från F till N .)

Därför kan definitionerna av limits och colimits sedan omformuleras i formen:

• En gräns för F är en universell morfism från Δ till F .
• En kogräns av F är en universell morfism från F till Δ.

Adjunktioner

Liksom alla universella konstruktioner är bildandet av gränser och samgränser funktionellt till sin natur. Med andra ord, om varje diagram av form J har en gräns i C (för J liten) finns det en gränsfunktion

$\lim :{\mathcal {C}}^{\mathcal {J}}\to {\mathcal {C}}$

som tilldelar varje diagram sin gräns och varje naturlig transformation η : F → G den unika morfismen lim η : lim F → lim G pendling med motsvarande universella koner. Denna funktion är direkt angränsande till diagonalfunktionen Δ : C → C ^J . Denna adjunktion ger en bijektion mellan mängden av alla morfismer från N till lim F och mängden av alla koner från N till F

$\operatorname {Hom} (N,\lim F)\cong \operatorname {Cone} (N,F)$

vilket är naturligt i variablerna N och F . Mängden för denna adjunktion är helt enkelt den universella konen från lim F till F . Om indexkategorin J är ansluten (och icke-tom) så är enheten för adjunktionen en isomorfism så att lim är en vänsterinvers av Δ. Detta misslyckas om J inte är ansluten. Till exempel, om J är en diskret kategori, är komponenterna i enheten de diagonala morfismerna δ : N → N ^J .

Dubbelt, om varje diagram av form J har en colimit i C (för J liten) finns det en colimit funktor

$\operatörsnamn {colim} :{\mathcal {C}}^{\mathcal {J}}\to {\mathcal {C}}$

som tilldelar varje diagram dess kolimit. Denna funktion lämnas i anslutning till diagonalfunktionen Δ : C → C ^J , och en har en naturlig isomorfism

$\operatörsnamn {Hom} (\operatörsnamn {colim} F,N)\cong \operatörsnamn {Cocone} (F,N).$

Enheten för denna adjunktion är den universella kokongen från F till colim F . Om J är ansluten (och icke-tom) så är enheten en isomorfism, så att colim är en vänsterinvers av Δ.

Observera att både limit- och colimit-funktionerna är kovariansfunktioner .

Som representationer av funktioner

Se även: Limit och colimit of preheaves

Man kan använda Hom-funktioner för att relatera limits och colimits i en kategori C till limits i Set , kategorin av uppsättningar . Detta följer delvis av det faktum att den kovarianta Hom-funktorn Hom( N , –) : C → Set bevarar alla gränser i C . Genom dualitet måste den kontravarianta Hom-funktionen ta colimits till limits.

Om ett diagram F : J → C har en gräns i C , betecknat med lim F , finns det en kanonisk isomorfism

$\operatorname {Hom} (N,\lim F)\cong \lim \operatorname {Hom} (N,F-)$

vilket är naturligt i variabeln N . Här är funktorn Hom( N , F –) sammansättningen av Hom-funktorn Hom( N , –) med F . Denna isomorfism är den unika som respekterar de begränsande konerna.

Man kan använda ovanstående förhållande för att definiera gränsen för F i C . Det första steget är att observera att gränsen för funktionatorn Hom( N , F –) kan identifieras med uppsättningen av alla koner från N till F :

$\lim \operatörsnamn {Hom} (N,F-)=\operatörsnamn {Cone} (N,F).$

Den begränsande könen ges av familjen av kartor π _X : Cone( N , F ) → Hom( N , FX ) där π _X ( ψ ) = ψ _X . Om man ges ett objekt L av C tillsammans med en naturlig isomorfism Φ : Hom( L , –) → Cone(–, F ), kommer objektet L att vara en gräns för F med den begränsande konen som ges av Φ _L (id _L ). På ett fint språk betyder det att en gräns för F är en representation av funktionskonen (–, F ) : C → Set .

Dubbelt, om ett diagram F : J → C har en kogräns i C , betecknad kolim F , finns det en unik kanonisk isomorfism

$\operatorname {Hom} (\operatörsnamn {colim} F,N)\cong \lim \operatornamn {Hom} (F-, N)$

vilket är naturligt i variabeln N och respekterar de sambegränsande konerna. Genom att identifiera gränsen för Hom( F –, N ) med mängden Cocone( F , N ), kan detta samband användas för att definiera kogränsen för diagrammet F som en representation av funktorn Cocone( F , –).

Utbyte av gränser och samgränser av uppsättningar

Låt jag vara en finit kategori och J vara en liten filtrerad kategori . För alla bifunktörer

$F:I\times J\to \mathbf {Set} ,$

det finns en naturlig isomorfism

$\operatörsnamn {colim} \limits _{J}\lim _{I}F(i,j)\högerpil \lim _{I}\operatörsnamn {colim} \limits _{J}F(i,j ).$

Med ord, filtrerade samgränser i Ange pendling med ändliga gränser. Det gäller också att små samgränser pendlar med små gränser.

Funktioner och gränser

Om F : J → C är ett diagram i C och G : C → D är en funktionor så får man genom sammansättning (kom ihåg att ett diagram bara är en funktionor) ett diagram GF : J → D . En naturlig fråga är då:

"Hur är gränserna för GF relaterade till de för F ?"

Bevarande av gränser

En funktion G : C → D inducerar en avbildning från Cone( F ) till Cone( GF ): om Ψ är en kon från N till F så är GΨ en kon från GN till GF . Funktionen G sägs bevara gränserna för F om ( GL , Gφ ) är en gräns för GF närhelst ( L , φ ) är en gräns för F. (Observera att om gränsen för F inte existerar, så bevarar G gränserna för F tomlöst .)

En funktor G sägs bevara alla gränser för form J om den bevarar gränserna för alla diagram F : J → C . Till exempel kan man säga att G bevarar produkter, utjämnare, pullbacks etc. En kontinuerlig funktor är en som bevarar alla små gränser.

Man kan göra analoga definitioner för kogränser. Till exempel bevarar en funktor G kogränserna för F om G ( L , φ ) är en kogräns för GF närhelst ( L , φ ) är en kogräns för F . En kokontinuerlig funktion är en som bevarar alla små kogränser.

Om C är en fullständig kategori , så är, enligt ovanstående existenssats för gränser, en funktion G : C → D kontinuerlig om och endast om den bevarar (små) produkter och utjämnare. Dubbelt G kokontinuerligt om och endast om det bevarar (små) biprodukter och samutjämnare.

En viktig egenskap hos adjoint-funktioner är att varje höger adjoint-funktion är kontinuerlig och varje vänster adjoint-funktionor är kokontinuerlig. Eftersom adjunktfunktioner finns i överflöd, ger detta många exempel på kontinuerliga och kokontinuerliga funktioner.

För ett givet diagram F : J → C och funktion G : C → D , om både F och GF har specificerade gränser finns det en unik kanonisk morfism

$\tau _{F}:G\lim F\to \lim GF$

som respekterar motsvarande gränskoner. Funktionen G bevarar gränserna för F om och endast denna karta är en isomorfism. Om kategorierna C och D har alla gränser för form J så är lim en funktion och morfismerna τ _F bildar komponenterna i en naturlig transformation

$\tau :G\lim \to \lim G^{J}.$

Funktionen G bevarar alla gränser för form J om och endast om τ är en naturlig isomorfism. I denna mening kan funktorn G sägas pendla med gränser ( upp till en kanonisk naturlig isomorfism).

Bevarande av gränser och kogränser är ett begrepp som endast gäller för samvarianta funktorer. För kontravarianta funktorer skulle motsvarande begrepp vara en funktor som tar kogränser till gränser, eller en som tar gränser till kogränser.

Upphävande av gränser

En funktion G : C → D sägs lyfta gränserna för ett diagram F : J → C om närhelst ( L , φ ) är en gräns för GF det finns en gräns ( L ′, φ ′) för F så att G ( L ) ′, φ ′) = ( L , φ ). En funktion G lyfter gränser för form J om den lyfter gränser för alla diagram av form J . Man kan därför prata om lyftprodukter, utjämnare, pullbacks etc. Slutligen säger man att G lyfter gränser om det lyfter alla gränser. Det finns dubbla definitioner för lyft av kogränser.

En funktion G lyfter gränser unikt för ett diagram F om det finns en unik förbildskon ( L ′, φ ′) så att ( L ′, φ ′) är en gräns för F och G ( L ′ , φ ′) = ( L , φ ). Man kan visa att G lyfter gränser unikt om och bara om det lyfter gränser och är amnestisk .

Upphävande av gränser är tydligt relaterat till bevarande av gränser. Om G höjer gränserna för ett diagram F och GF har en gräns, så har F också en gräns och G bevarar gränserna för F . Det följer att:

• Om G lyfter gränser för all form J och D har alla gränser för form J , så har C också alla gränser för form J och G bevarar dessa gränser.
• Om G lyfter alla små gränser och D är komplett, så är C också komplett och G är kontinuerlig.

De dubbla uttalandena för colimits är lika giltiga.

Skapande och reflektion av gränser

Låt F : J → C vara ett diagram. En funktion G : C → D sägs det

• skapa gränser för F om närhelst ( L , φ ) är en gräns för GF det finns en unik kon ( L ′, φ ′) till F så att G ( L ′, φ ′) = ( L , φ ), och vidare, denna kon är en gräns för F .
• reflektera gränser för F om varje kon till F vars bild under G är en gräns för GF redan är en gräns för F .

Dubbelt kan man definiera skapande och reflektion av kolimiter.

Följande påståenden kan lätt ses som likvärdiga:

• Funktionen G skapar gränser.
• Funktionen G lyfter gränser unikt och reflekterar gränser.

Det finns exempel på funktioner som lyfter gränser unikt men varken skapar eller reflekterar dem.

Exempel

• Varje representativ funktion C → Set bevarar gränser (men inte nödvändigtvis medgränser). I synnerhet, för alla objekt A av C , gäller detta för den kovarianta Hom-funktorn Hom( A ,–) : C → Set .
• Den glömska funktorn U : Grp → Set skapar (och bevarar) alla små gränser och filtrerade samgränser ; U bevarar dock inte biprodukter. Denna situation är typisk för algebraiska glömska funktorer.
• Den fria funktorn F : Set → Grp (som tilldelar varje uppsättning S den fria gruppen över S ) lämnas intill glömsk funktion U och är därför kokontinuerlig. Detta förklarar varför den fria produkten av två fria grupper G och H är den fria gruppen som genereras av den disjunkta föreningen av generatorerna av G och H.
• Inklusionsfunktionen Ab → Grp skapar gränser men bevarar inte samprodukter (samprodukten av två abelska grupper är den direkta summan ).
• Den glömska funktorn Top → Set lyfter gränser och colimiter unikt men skapar ingendera.
• Låt Met _c vara kategorin av metriska rum med kontinuerliga funktioner för morfismer. Den glömska funktorn Met _c → Set lyfter ändliga gränser men lyfter dem inte unikt.

En anteckning om terminologi

Äldre terminologi hänvisade till gränser som "inversa gränser" eller "projektiva gränser" och till samgränser som "direkta gränser" eller "induktiva gränser". Detta har varit källan till mycket förvirring.

Det finns flera sätt att komma ihåg den moderna terminologin. För det första,

• kokkärnor,
• samprodukter,
• coequalizers, och
• koddomäner

är typer av kogränser, medan

• kärnor,
• Produkter
• utjämnare och
• domäner

är typer av gränser. För det andra, prefixet "co" antyder "första variabeln i ${\displaystyle \operatörsnamn {Hom} } "$ . Termer som "cohomology" och "cofibration" har alla en något starkare association med den första variabeln, dvs den kontravarianta variabeln i $\operatorname {Hom}$ bifunctor.

Se även

• Kartesisk sluten kategori – Typ av kategori i kategoriteori
• Equalizer (matematik) – Uppsättning argument där två eller flera funktioner har samma värde
• Omvänd gräns – Konstruktion i kategoriteori
• Produkt (kategoriteori) – Generaliserat objekt i kategoriteori

Vidare läsning

•   Adámek, Jiří; Horst Herrlich; George E. Strecker (1990). Abstrakta och konkreta kategorier (PDF) . John Wiley & Sons. ISBN 0-471-60922-6 .
•    Mac Lane, Saunders (1998). Kategorier för den arbetande matematikern . Graduate Texts in Mathematics . Vol. 5 (andra upplagan). Springer-Verlag . ISBN 0-387-98403-8 . Zbl 0906.18001 .
•   Borceux, Francis (1994). "Gränser". Handbok i kategorisk algebra . Encyclopedia of mathematics and its applications 50-51, 53 [dvs. 52]. Vol. 1. Cambridge University Press. ISBN 0-521-44178-1 .

externa länkar

• Interaktiv webbsida som genererar exempel på limits och colimits i kategorin ändliga uppsättningar. Skrivet av Jocelyn Paine .
• Gräns ​​vid n Lab