Symmetrisk monoidal kategori

I kategoriteorin , en gren av matematiken , är en symmetrisk monoidal kategori en monoidal kategori (dvs en kategori där en "tensorprodukt" $\otimes$ definieras) så att tensorprodukten är symmetrisk (dvs. $A\otimes B$ är, i en viss strikt mening, naturligt isomorf till $B\otimes A$ för alla objekt $A$ och $B$ i kategorin) . Ett av de prototypiska exemplen på en symmetrisk monoidal kategori är kategorin vektorrum över något fast fält k, med användning av den vanliga tensorprodukten av vektorrum .

Definition

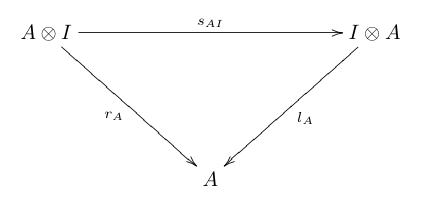
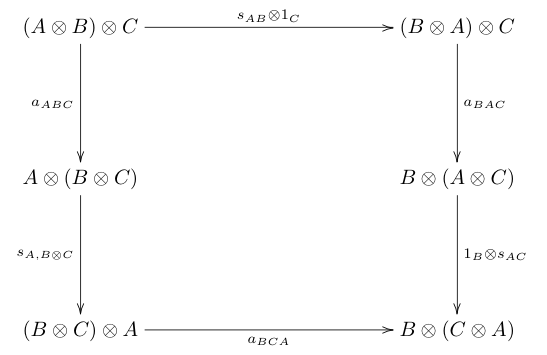
En symmetrisk monoidal kategori är en monoidal kategori ( C , ⊗, I ) så att det för varje par A , B av objekt i C finns en isomorfism $s_{AB }:A\otimes B\to B\otimes A$ kallas byteskartan som är naturlig i både A och B och sådan att följande diagram pendlar:

• Enhetens koherens:

  

• Den associativa koherensen:

  

• Den omvända lagen:

  

I diagrammen ovan är a , l och r associativitetsisomorfism, vänster enhet isomorfism respektive höger enhet isomorfism.

Exempel

Några exempel och icke-exempel på symmetriska monoidala kategorier:

• Kategorin av uppsättningar . Tensorprodukten är den mängdteoretiska kartesiska produkten, och vilken singleton som helst kan fixeras som enhetsobjekt.
• Kategorin av grupper . Liksom tidigare är tensorprodukten bara den kartesiska produkten av grupper, och den triviala gruppen är enhetsobjektet.
• Mer generellt är alla kategorier med ändliga produkter, det vill säga en kartesisk monoidal kategori , symmetrisk monoidal. Tensorprodukten är den direkta produkten av objekt, och varje terminalobjekt (tom produkt) är enhetsobjektet.
• Kategorin av bimoduler över en ring R är monoidal (med användning av den vanliga tensorprodukten av moduler), men inte nödvändigtvis symmetrisk. Om R är kommutativ är kategorin av vänster R -moduler symmetrisk monoidal. Den senare exempelklassen inkluderar kategorin för alla vektorrum över ett givet fält.
• Givet ett fält k och en grupp (eller en Lie-algebra över k ), är kategorin för alla k -linjära representationer av gruppen (eller av Lie-algebra) en symmetrisk monoidal kategori. Här används standardtensorprodukten av representationer.
• Kategorierna ( Ste , $\circledast$ ) och ( Ste , $\odot$ ) av stereotypa utrymmen över ${\mathbb {C} }$ är symmetriska monoidala, och dessutom ( Ste , $\circledast$ ) är en sluten symmetrisk monoidal kategori med den interna hom-funktorn $\oslash$ .

Egenskaper

Klassificeringsutrymmet (geometrisk realisering av nerven ) för en symmetrisk monoidal kategori är ett $E_{\infty }$ utrymme, så dess slutförande av gruppen är ett oändligt looprum .

Specialiseringar

En dolksymmetrisk monoidal kategori är en symmetrisk monoidal kategori med en kompatibel dolkstruktur .

Ett kosmos är en komplett medkomplett sluten symmetrisk monoidal kategori.

Generaliseringar

I en symmetrisk monoidal kategori är de naturliga isomorfismerna $s_{AB}:A\otimes B\to B\otimes A$ sina egna inverser i den meningen att $s_{BA}\circ s_{AB}=1_{A\otimes B}$ . Om vi ​​överger detta krav (men fortfarande kräver att $A\otimes B$ är naturligt isomorf till $B\otimes A$ ), får vi den mer allmänna uppfattningen om en flätad monoidal kategori .

• Symmetrisk monoidal kategori vid n Lab
• Den här artikeln innehåller material från kategorin Symmetrisk monoidal på PlanetMath , som är licensierad under licensen Creative Commons Attribution/Dela Lika .