Kotte (kategoriteori)

I kategoriteorin , en gren av matematiken , är konen av en funktor ett abstrakt begrepp som används för att definiera gränsen för den funktorn . Koner gör andra framträdanden i kategoriteorin också.

Definition

Låt F : J → C vara ett diagram i C . Formellt är ett diagram inget annat än en funktion från J till C . Ändringen i terminologi speglar det faktum att vi tänker på F som indexerande en familj av objekt och morfismer i C . Kategorin J är tänkt som en "indexkategori" . Man bör överväga detta i analogi med konceptet med en indexerad familj av objekt i mängdteorin . Den primära skillnaden är att här har vi morfismer också. Således, till exempel, när J är en diskret kategori , motsvarar den närmast idén om en indexerad familj i mängdteorin. Ett annat vanligt och mer intressant exempel tar J för att vara ett span . J kan också anses vara den tomma kategorin, vilket leder till de enklaste konerna.

Låt N vara ett objekt av C . En kon från N till F är en familj av morfismer

$\psi _{X}\colon N\to F(X)\,$

för varje objekt X av J , så att för varje morfism f : X → Y i J pendlar följande diagram :

Den (vanligtvis oändliga) samlingen av alla dessa trianglar kan (delvis) avbildas i form av en kon med spetsen N . Konen ψ sägs ibland ha vertex N och bas F .

Man kan också definiera den dubbla uppfattningen om en kon från F till N (även kallad en co-cone ) genom att vända på alla pilar ovan. En co-kon från F till N är uttryckligen en familj av morfismer

$\psi _{X}\kolon F(X)\to N\,$

för varje objekt X av J , så att för varje morfism f : X → Y i J pendlar följande diagram:

Likvärdiga formuleringar

Vid första anblick verkar koner vara något onormala konstruktioner i kategoriteorin. De är kartor från ett objekt till en funktor (eller vice versa). I enlighet med kategoriteorin skulle vi vilja definiera dem som morfismer eller objekt i någon lämplig kategori. Faktum är att vi kan göra båda.

Låt J vara en liten kategori och låt C ^J vara kategorin av diagram av typ J i C (detta är inget annat än en funktionskategori ). Definiera diagonalfunktionen Δ : C → C ^J enligt följande: Δ( N ) : J → C är den konstanta funktorn till N för alla N i C .

Om F är ett diagram av typ J i C , är följande påståenden ekvivalenta:

• ψ är en kon från N till F
• ψ är en naturlig transformation från Δ( N ) till F
• ( N , ψ) är ett objekt i kommakategorin ( Δ ↓ F )

De dubbla uttalandena är också likvärdiga:

• ψ är en co-kon från F till N
• ψ är en naturlig transformation från F till Δ( N )
• ( N , ψ) är ett objekt i kommakategorin ( F ↓ Δ)

Dessa påståenden kan alla verifieras genom en enkel tillämpning av definitionerna. När vi tänker på koner som naturliga transformationer ser vi att de bara är morfismer i C ^J med källan (eller målet) en konstant funktion.

Kategori av kottar

Genom ovanstående kan vi definiera kategorin av koner till F som kommakategorin (Δ ↓ F ). Morfismer av kottar är då bara morfismer i denna kategori. Denna ekvivalens har sin rötter i observationen att en naturlig karta mellan konstanta funktorer Δ( N ), Δ( M ) motsvarar en morfism mellan N och M . I denna mening verkar diagonalfunktionen trivialt på pilar. På liknande sätt ger nedskrivning av definitionen av en naturlig karta från en konstant funktion Δ( N ) till F samma diagram som ovan. Som man kan förvänta sig är en morfism från en kon ( N , ψ) till en kon ( L , φ) bara en morfism N → L så att alla de "uppenbara" diagrammen pendlar (se det första diagrammet i nästa avsnitt).

Likaså är kategorin medkoner från F kommakategorin ( F ↓ Δ).

Universal koner

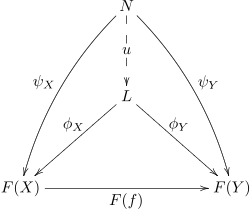
Limits och colimits definieras som universella koner . Det vill säga kottar genom vilka alla andra kottar faktor. En kon φ från L till F är en universell kon om det för någon annan kon ψ från N till F finns en unik morfism från ψ till φ.

På motsvarande sätt är en universell kon till F en universell morfism från Δ till F (tänkt som ett objekt i C ^J ), eller ett terminalobjekt i (Δ ↓ F ).

Dubbelt sett är en kon φ från F till L en universell kon om det för någon annan kon ψ från F till N finns en unik morfism från φ till ψ.

På motsvarande sätt är en universell kon från F en universell morfism från F till Δ, eller ett initialt objekt i ( F ↓ Δ).

Gränsen för F är en universell kon till F , och colimiten är en universell kon från F . Som med alla universella konstruktioner är det inte garanterat att universella koner finns för alla diagram F , men om de finns är de unika upp till en unik isomorfism (i kommakategorin (Δ ↓ F )).

Se även

• Invers gräns#Koner – Konstruktion i kategoriteori

•   Mac Lane, Saunders (1998). Kategorier för den arbetande matematikern (2:a uppl.). New York: Springer. ISBN 0-387-98403-8 .
•   Borceux, Francis (1994). "Gränser". Handbok i kategorisk algebra . Encyclopedia of mathematics and its applications 50-51, 53 [dvs. 52]. Vol. 1. Cambridge University Press. ISBN 0-521-44178-1 .

externa länkar

• Cone på n Lab