Modellkategori

Inom matematiken , särskilt i homotopiteorin , är en modellkategori en kategori med distingerade klasser av morfismer ("pilar") som kallas " svaga ekvivalenser ", " fibrationer " och " samfibrer " som uppfyller vissa axiom som relaterar dem. Dessa abstraherar från kategorin topologiska utrymmen eller kedjekomplex ( härledd kategoriteori ). Konceptet introducerades av Daniel G. Quillen ( 1967 ).

Under de senaste decennierna har språket för modellkategorier använts i vissa delar av algebraisk K -teori och algebraisk geometri , där homotopi-teoretiska tillvägagångssätt ledde till djupa resultat.

Motivering

Modellkategorier kan ge en naturlig miljö för homotopi-teori : kategorin topologiska utrymmen är en modellkategori, med homotopin som motsvarar den vanliga teorin. På liknande sätt tillåter objekt som betraktas som utrymmen ofta en modellkategoristruktur, till exempel kategorin för enkla uppsättningar .

En annan modellkategori är kategorin av kedjekomplex av R -moduler för en kommutativ ring R . Homotopi teori i detta sammanhang är homologisk algebra . Homologi kan sedan ses som en typ av homotopi, vilket tillåter generaliseringar av homologi till andra objekt, såsom grupper och R -algebror , en av de första stora tillämpningarna av teorin. På grund av ovanstående exempel angående homologi, betraktas studien av slutna modellkategorier ibland som homotopisk algebra .

Formell definition

Den definition som Quillen ursprungligen gav var den av en sluten modellkategori, vars antaganden verkade starka vid den tiden, vilket motiverade andra att försvaga vissa av antagandena för att definiera en modellkategori. I praktiken har distinktionen inte visat sig signifikant och de senaste författarna (t.ex. Mark Hovey och Philip Hirschhorn) arbetar med slutna modellkategorier och släpper helt enkelt adjektivet "stängd".

Definitionen har separerats från en modellstruktur för en kategori och sedan ytterligare kategoriska villkor för den kategorin, vars nödvändighet kan tyckas omotiverad till en början men blir viktig senare. Följande definition följer den som ges av Hovey.

En modellstruktur i en kategori C består av tre distingerade klasser av morfismer (motsvarande underkategorier): svaga ekvivalenser , fibrationer och kofibreringar och två funktionella faktoriseringar $(\alpha ,\beta )$ och $(\gamma ,\delta )$ med förbehåll för följande axiom. En fibration som också är en svag ekvivalens kallas en acyklisk (eller trivial ) fibration och en cofibration som också är en svag ekvivalens kallas en acyklisk (eller trivial ) cofibration (eller ibland kallad anodyn morfism ).

Axiom

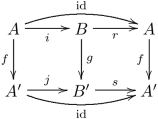
1. Retracts : om g är en morfism som tillhör en av de utmärkande klasserna, och f är en retract av g (som objekt i pilkategorin $C^{2}$ , där 2 är den 2-elements ordnade mängden ), då hör f till samma framstående klass. Kravet på att f är ett tillbakadragande av g betyder uttryckligen att det finns i , j , r och s , så att följande diagram pendlar:

   

2. 2 av 3 : om f och g är kartor i C så att gf definieras och vilka två som helst av dessa är svaga ekvivalenser så är den tredje det också.
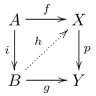
3. Lyftning : acykliska samfibrer har den vänstra lyftegenskapen med avseende på fibrer, och samfibrer har den vänstra lyftegenskapen med avseende på acykliska fibrer. Explicit, om den yttre kvadraten i följande diagram pendlar, där i är en samfibrering och p är en fibrering, och i eller p är acyklisk, så finns det h som fullbordar diagrammet.

   

4. Faktorisering :
   • varje morfism f i C kan skrivas som $p\circ i$ för en fibration p och en acyklisk cofibration i ;
   • varje morfism f i C kan skrivas som $p\circ i$ för en acyklisk fibrering p och en cofibration i .

En modellkategori är en kategori som har en modellstruktur och alla (små) limits och colimits , dvs en komplett och cokomplett kategori med en modellstruktur.

Definition via svaga faktoriseringssystem

Ovanstående definition kan kortfattat formuleras med följande ekvivalenta definition: en modellkategori är en kategori C och tre klasser av (så kallade) svaga ekvivalenser W , fibrationer F och cofibrationer C så att

• C har alla gränser och kogränser,

• $(C\cap W,F)$ är ett svagt faktoriseringssystem ,

• $(C,F\cap W)$ är ett svagt faktoriseringssystem
• $W$ uppfyller egenskapen 2 av 3.

De första konsekvenserna av definitionen

Axiomen antyder att två av de tre klasserna av kartor bestämmer den tredje (t.ex. samfibreringar och svaga ekvivalenser bestämmer fibrationer).

Definitionen är också självdual: om C är en modellkategori, så tillåter dess motsatta kategori ${\mathcal {C}}^{op}$ också en modellstruktur så att svaga ekvivalenser motsvarar deras motsatser, fibrationer motsatser till kofibrer och kofibrer motsatser till fibrationer.

Exempel

Topologiska utrymmen

Kategorien topologiska utrymmen, Top , tillåter en standardmodellkategoristruktur med de vanliga (Serre) fibrerna och med svaga ekvivalenser som svaga homotopiekvivalenser. Samfibreringarna är inte den vanliga uppfattningen som finns här , utan snarare den smalare klassen av kartor som har den vänstra lyftegenskapen med avseende på de acykliska Serre-fibrationerna. På motsvarande sätt är de tillbakadragen av de relativa cellkomplexen, som förklaras till exempel i Hovey's Model Categories . Denna struktur är inte unik; i allmänhet kan det finnas många modellkategoristrukturer i en given kategori. För kategorin topologiska utrymmen ges en annan sådan struktur av Hurewicz-fibrationer och standardkofibrationer, och de svaga ekvivalenserna är de (starka) homotopi-ekvivalenserna .

Kedjekomplex

Kategorin av (icke negativt graderade) kedjekomplex av R -moduler bär minst två modellstrukturer, som båda är framträdande i homologisk algebra:

• svaga ekvivalenser är kartor som inducerar isomorfismer i homologi;
• cofibrations är kartor som är monomorfismer i varje grad med projektiv kokkärna ; och
• fibrationer är kartor som är epimorfismer i varje grad som inte är noll

eller

• svaga ekvivalenser är kartor som inducerar isomorfismer i homologi;
• fibrationer är kartor som är epimorfismer i varje grad med injektiv kärna ; och
• kofibrationer är kartor som är monomorfismer i varje grad som inte är noll.

Detta förklarar varför Ext-grupper av R -moduler kan beräknas genom att antingen lösa källan projektivt eller målet injektivt. Dessa är kofibranter eller fibrantersättningar i respektive modellstrukturer.

Kategorin av godtyckliga kedjekomplex av R -moduler har en modellstruktur som definieras av

• svaga ekvivalenser är kedjehomotopiekvivalenser av kedjekomplex;
• kofibrationer är monomorfismer som är uppdelade som morfismer av underliggande R -moduler; och
• fibrationer är epimorfismer som delas upp som morfismer av underliggande R -moduler.

Ytterligare exempel

Andra exempel på kategorier som tillåter modellstrukturer inkluderar kategorin för alla små kategorier, kategorin för enkla uppsättningar eller enkla presheaves på en liten Grothendieck-plats, kategorin av topologiska spektra och kategorierna av enkla spektra eller preheaves av enkla spektra på en liten Grothendieck webbplats.

Enkla objekt i en kategori är en frekvent källa till modellkategorier; till exempel enkla kommutativa ringar eller enkla R -moduler naturliga modellstrukturer. Detta följer eftersom det finns en adjunktion mellan enkla uppsättningar och enkla kommutativa ringar (givna av de glömska och fria funktionerna), och i trevliga fall kan man lyfta modellstrukturer under en adjunktion.

En enkel modellkategori är en enkel kategori med en modellstruktur som är kompatibel med den förenklade strukturen.

Med tanke på vilken kategori C som helst och en modellkategori M , är under vissa extra hypoteser även kategorin av funktioner Fun ( C , M ) (även kallade C -diagram i M ) en modellkategori. Faktum är att det alltid finns två kandidater för distinkta modellstrukturer: i den ena, den så kallade projektiva modellstrukturen, är fibrationer och svaga ekvivalenser de kartor av funktiontorer som är fibrationer och svaga ekvivalenser när de utvärderas vid varje objekt av C . Dubbelt är den injektiva modellstrukturen liknande med kofibreringar och svaga ekvivalenser istället. I båda fallen ges den tredje klassen av morfismer av ett lyfttillstånd (se nedan). I vissa fall, när kategori C är en Reedy-kategori, finns det en tredje modellstruktur som ligger mellan projektiv och injektiv.

Processen att tvinga vissa kartor att bli svaga ekvivalenser i en ny modellkategoristruktur på samma underliggande kategori kallas Bousfield-lokalisering . Till exempel kan kategorin för enkla skivor erhållas som en Bousfield-lokalisering av modellkategorin för enkla förskivor .

Denis-Charles Cisinski har utvecklat en allmän teori om modellstrukturer för kategorier av preheaf (generalizing simplicial sets, som är preheaves på simplex-kategorin ).

Om C är en modellkategori, så är kategorin Pro( C ) av pro-objekt i C också det . En modellstruktur på Pro( C ) kan emellertid också konstrueras genom att pålägga C en svagare uppsättning axiom .

Vissa konstruktioner

Varje sluten modellkategori har ett terminalobjekt genom fullständighet och ett initialobjekt genom cokompletthet, eftersom dessa objekt är gränsen respektive medgränsen för det tomma diagrammet. Givet ett objekt X i modellkategorin, om den unika kartan från det initiala objektet till X är en kofibrering, sägs X vara kofibrant . Analogt, om den unika kartan från X till terminalobjektet är en fibrering, sägs X vara fibrant .

Om Z och X är objekt av en modellkategori så att Z är kofibrant och det finns en svag ekvivalens från Z till X så sägs Z vara en kofibrant ersättning för X . På liknande sätt, om Z är fibrant och det finns en svag ekvivalens från X till Z så sägs Z vara en fibrant ersättning för X . I allmänhet är inte alla föremål fibrer eller kofibrerande, även om detta ibland är fallet. Till exempel är alla objekt cofibrant i standardmodellkategorin av enkla uppsättningar och alla objekt är fibranta för standardmodellkategoristrukturen som ges ovan för topologiska utrymmen.

Vänster homotopi definieras med avseende på cylinderobjekt och höger homotopi definieras med avseende på banrumsobjekt . Dessa föreställningar sammanfaller när domänen är kofibrant och codomänen är fibrant. I så fall definierar homotopi en ekvivalensrelation på hemmängderna i modellkategorin som ger upphov till homotopiklasser.

Karakteriseringar av fibrer och samfibrer genom lyftegenskaper

Samfibrer kan karakteriseras som de kartor som har den vänstra lyftegenskapen med avseende på acykliska fibrer, och acykliska samfibrer karakteriseras som de kartor som har den vänstra lyftegenskapen med avseende på fibrer. På liknande sätt kan fibrer karakteriseras som de kartor som har den rätta lyftegenskapen med avseende på acykliska samfibrer, och acykliska fibrer karakteriseras som de kartor som har den rätta lyftegenskapen med avseende på samfibrer.

Homotopi och kategorin homotopi

Homotopikategorin för en modellkategori C är lokaliseringen av C med avseende på klassen av svaga ekvivalenser. Denna definition av homotopikategori beror inte på valet av fibrer och samfibrer. Klasserna av fibrer och samfibrer är emellertid användbara för att beskriva homotopikategorin på ett annat sätt och i synnerhet för att undvika mängdteoretiska problem som uppstår vid allmänna lokaliseringar av kategorier. Närmare bestämt säger "grundsatsen för modellkategorier" att homotopikategorin för C är ekvivalent med kategorin vars objekt är objekten i C som är både fibrant och cofibrant, och vars morfismer är vänsterhomotopiklasser av kartor (motsvarande höger). homotopiklasser av kartor) enligt definitionen ovan. (Se till exempel Model Categories by Hovey, Thm 1.2.10)

Om man tillämpar detta på kategorin topologiska utrymmen med modellstrukturen som ges ovan, är den resulterande homotopikategorin ekvivalent med kategorin CW-komplex och homotopiklasser av kontinuerliga kartor, varifrån namnet kommer.

Quillen tillägg

Ett par angränsande funktorer

$F:C\leftrightarrows D:G$

mellan två modellkategorier C och D kallas en Quillen-adjunktion om F bevarar samfibrer och acykliska fibrer eller, på motsvarande sätt av de slutna modellens axiom, så att G bevarar fibrer och acykliska fibrer. I detta fall F och G en adjunktion

$LF:Ho(C)\leftrightarrows Ho(D):RG$

mellan homotopikategorierna. Det finns också ett uttryckligt kriterium för att det senare ska vara en ekvivalens ( F och G kallas då för Quillen-ekvivalens ).

Ett typiskt exempel är standardadjunktionen mellan enkla uppsättningar och topologiska utrymmen:

$|-|:\mathbf {sSet} \leftrightarrows \mathbf {Top} :Sing$

involverar den geometriska realiseringen av en enkel uppsättning och de singulära kedjorna i något topologiskt utrymme. Kategorierna sSet och Top är inte likvärdiga, men deras homotopikategorier är det. Därför används enkla uppsättningar ofta som modeller för topologiska utrymmen på grund av denna likvärdighet av homotopikategorier.

Se även

• (∞,1)-kategori
• Cocycle kategori
• Stabil modellkategori

Anteckningar

• Denis-Charles Cisinski: Les préfaisceaux commes modèles des types d'homotopie , Astérisque, (308) 2006, xxiv+392 pp.
•   Dwyer, William G .; Spaliński, Jan (1995), "Homotopy theories and model categories" (PDF) , Handbook of algebraic topology , Amsterdam: North-Holland, s. 73–126, doi : 10.1016/B978-044481779-2/50003-1 , 50003-1 1361887
•   Philip S. Hirschhorn: Model Categories and Their Localizations , 2003, ISBN 0-8218-3279-4 .
•   Mark Hovey: Model Categories , 1999, ISBN 0-8218-1359-5 .
•   Klaus Heiner Kamps och Timothy Porter: Abstrakt homotopi och enkel homotopi teori , 1997, World Scientific, ISBN 981-02-1602-5 .
• Georges Maltsiniotis: La théorie de l'homotopie de Grothendieck . Astérisque, (301) 2005, vi+140 s.

•    Riehl, Emily (2014), Categorical Homotopy Theory , Cambridge University Press, DOI : 10.1017/CBO9781107261457 , ISBN 978-1-107-04845-4 , MR 3221774

•   Quillen, Daniel G. (1967), Homotopicalbåt , Legat i mathtics i matematik 43, vol. 43, Berlin, New York: Springer-Verlag , doi : 10.1007/BFb0097438 , MR 0223432

•    Balchin, Scott (2021), A Handbook of Model Categories , Springer, doi : 10.1007/978-3-035-07 5 035-7N 5 -3-030-75034-3 , MR 4385504

Vidare läsning

• "Behöver vi fortfarande modellkategorier?"
• "(oändlighet,1)-kategorier direkt från modellkategorier"
• Paul Goerss och Kristen Schemmerhorn, Modellkategorier och enkla metoder

externa länkar

• Modellkategori på n Lab
• Modellkategori i Joyals catlab