Stor kanonisk ensemble

Inom statistisk mekanik är den stora kanoniska ensemblen (även känd som den makrokanoniska ensemblen ) den statistiska ensemblen som används för att representera de möjliga tillstånden i ett mekaniskt system av partiklar som är i termodynamisk jämvikt (termisk och kemisk) med en reservoar. Systemet sägs vara öppet i den meningen att systemet kan byta energi och partiklar med en reservoar, så att olika möjliga tillstånd i systemet kan skilja sig åt både i sin totala energi och totalt antal partiklar. Systemets volym, form och andra externa koordinater hålls desamma i alla möjliga tillstånd av systemet.

De termodynamiska variablerna för den stora kanoniska ensemblen är kemisk potential (symbol: µ ) och absolut temperatur (symbol: T ) . Ensemblen är också beroende av mekaniska variabler såsom volym (symbol: V ) som påverkar arten av systemets interna tillstånd. Denna ensemble kallas därför ibland µVT- ensemblen , eftersom var och en av dessa tre kvantiteter är konstanter för ensemblen.

Grunderna

Enkelt uttryckt tilldelar den stora kanoniska ensemblen en sannolikhet P till varje distinkt mikrotillstånd som ges av följande exponential:

$P=e^{\frac {\Omega +\mu NE}{kT}},$

där N är antalet partiklar i mikrotillståndet och E är mikrotillståndets totala energi. k är Boltzmanns konstant .

Talet Ω är känt som den stora potentialen och är konstant för ensemblen. Sannolikheterna och Ω kommer dock att variera om olika µ , V ​​, T väljs. Den stora potentialen Ω har två roller: att tillhandahålla en normaliseringsfaktor för sannolikhetsfördelningen (sannolikheterna, över hela uppsättningen av mikrotillstånd, måste läggas till ett); och många viktiga ensemblemedelvärden kan beräknas direkt från funktionen Ω( µ , V ​​, T ) .

I det fall där mer än en sorts partikel tillåts variera i antal, generaliserar sannolikhetsuttrycket till

$P=e^{\frac {\Omega +\mu _{1}N_{1} +\mu _{2}N_{2}+\ldots +\mu _{s}N_{s}-E}{kT}},$

där µ ₁ är den kemiska potentialen för den första typen av partiklar, N ₁ är antalet av den typen av partiklar i mikrotillståndet, µ ₂ är den kemiska potentialen för den andra typen av partiklar och så vidare ( s är antalet distinkta typer av partiklar). Dessa partikelantal bör dock definieras noggrant (se anmärkningen om bevarande av partikelantal nedan).

Fördelningen av den stora kanoniska ensemblen kallas av vissa författare generaliserad Boltzmann-distribution .

Stora ensembler är lämpliga för användning när man beskriver system som elektronerna i en ledare eller fotonerna i en kavitet, där formen är fixerad men energin och antalet partiklar lätt kan fluktuera på grund av kontakt med en reservoar (t.ex. en elektrisk mark eller mörk yta , i dessa fall). Den stora kanoniska ensemblen ger en naturlig miljö för en exakt härledning av Fermi-Dirac-statistiken eller Bose-Einstein-statistiken för ett system av icke-interagerande kvantpartiklar (se exempel nedan).

Anmärkning om formulering

En alternativ formulering för samma begrepp skriver sannolikheten som $\textstyle P={\frac {1}{\mathcal {Z}} }e^{(\mu NE)/(kT)}$ , med hjälp av den stora partitionsfunktionen $\textstyle {\mathcal {Z}}=e^{-\Omega /(kT)}$ snarare än den stora potentialen. Ekvationerna i den här artikeln (i termer av stor potential) kan omformuleras i termer av den stora partitionsfunktionen genom enkla matematiska manipulationer.

Tillämplighet

Den stora kanoniska ensemblen är den ensemble som beskriver de möjliga tillstånden i ett isolerat system som är i termisk och kemisk jämvikt med en reservoar (härledningen fortsätter längs linjer som är analoga med värmebadshärledningen av den normala kanoniska ensemblen, och kan hittas i Reif ). Den stora kanoniska ensemblen gäller system av alla storlekar, små som stora; det är bara nödvändigt att anta att reservoaren som den är i kontakt med är mycket större (dvs. att ta den makroskopiska gränsen ).

Villkoret att systemet är isolerat är nödvändigt för att säkerställa att det har väldefinierade termodynamiska storheter och evolution. I praktiken är det dock önskvärt att använda den stora kanoniska ensemblen för att beskriva system som är i direkt kontakt med reservoaren, eftersom det är den kontakten som säkerställer jämvikten. Användningen av den stora kanoniska ensemblen i dessa fall motiveras vanligtvis antingen 1) genom att anta att kontakten är svag, eller 2) genom att inkorporera en del av reservoaranslutningen i systemet som analyseras, så att sambandets påverkan på regionen av intresset är korrekt modellerat. Alternativt kan teoretiska tillvägagångssätt användas för att modellera påverkan av sambandet, vilket ger en öppen statistisk ensemble.

Ett annat fall där den stora kanoniska ensemblen uppträder är när man överväger ett system som är stort och termodynamiskt (ett system som är "i jämvikt med sig själv"). Även om de exakta förhållandena för systemet faktiskt inte tillåter variationer i energi eller partikelantal, kan den stora kanoniska ensemblen användas för att förenkla beräkningar av vissa termodynamiska egenskaper. Anledningen till detta är att olika termodynamiska ensembler ( mikrokanoniska , kanoniska ) blir likvärdiga i vissa aspekter med den stora kanoniska ensemblen, när systemet väl är mycket stort. Naturligtvis, för små system är de olika ensemblerna inte längre likvärdiga ens i medeltal. Som ett resultat kan den stora kanoniska ensemblen vara mycket felaktig när den appliceras på små system med fast partikelantal, såsom atomkärnor.

Egenskaper

• Unikhet : Den stora kanoniska ensemblen är unikt bestämd för ett givet system vid given temperatur och givna kemiska potentialer, och beror inte på godtyckliga val som val av koordinatsystem (klassisk mekanik) eller bas (kvantmekanik). Den stora kanoniska ensemblen är den enda ensemblen med konstant ${\displaystyle \mu} ,$ V , och T som reproducerar den grundläggande termodynamiska relationen .
• Statistisk jämvikt (steady state): En storslagen kanonisk ensemble utvecklas inte över tiden, trots att det underliggande systemet är i konstant rörelse. Faktum är att ensemblen bara är en funktion av de bevarade kvantiteterna i systemet (energi och partikelantal).
• Termisk och kemisk jämvikt med andra system : Två system, som vart och ett beskrivs av en stor kanonisk ensemble med lika temperatur och kemiska potentialer, som kommer i termisk och kemisk kontakt kommer att förbli oförändrade, och det resulterande kombinerade systemet kommer att beskrivas av en kombinerad kanonisk ensemble av samma temperatur och kemiska potentialer.
• Maximal entropi : För givna mekaniska parametrar (fast V ), är det stora kanoniska ensemblens medelvärde av logsannolikheten $-\langle \log P\rangle$ (även kallad "entropin") maximalt möjligt för vilken ensemble som helst (dvs. sannolikhetsfördelning P ) med samma $\langle E\rangle$ , $\langle N_{1}\rangle$ osv.
• Minsta storpotential : För givna mekaniska parametrar (fast V ) och givna värden på T , µ ₁ , …, µs _{ensemblemedelvärdet} , ${ \displaystyle \left\langle E+kT\log P-\mu _{1}N_{1}-\ldots \mu _{s}N_{s}\right\rangle } är den lägsta möjliga$ av någon ensemble.

Stor potential, ensemblemedelvärden och exakta skillnader

De partiella derivatorna av funktionen Ω( _µ 1 _, …, µs , V , T ) ger viktiga medelstorheter för stora kanoniska ensemblen:

• medelvärdena av antalet partiklar

  $\langle N_{1}\rangle =-{\frac {\frac \Omega }{\partial \mu _{1}}},\quad \ldots \quad \langle N_{s}\rangle =-{\frac {\partial \Omega }{\partial \mu _{s}} },$

• medeltrycket
  $\langle p\rangle =-{\frac {\partial \Omega }{\partial V}},$
• Gibbs -entropin
  $S=-k\langle \log P\rangle =-{\frac {\partial \Omega }{\partial T}} ,$
• och medelenergin
  $\langle E\rangle =\Omega +\langle N_{1}\rangle \mu _{1}\ldots +\langle N_{s}\rangle \mu _{s}+ST.$

Exakt differential : Från ovanstående uttryck kan det ses att funktionen Ω har den exakta differentialen

$d\Omega =-SdT-\langle N_{1}\rangle d\mu _{1}\ldots -\langle N_{s}\rangle d\mu _{s}-\langle p\rangle dV .$

Termodynamikens första lag : Genom att ersätta förhållandet ovan med ⟨ E ⟩ med den exakta differentialen för Ω , hittas en ekvation som liknar termodynamikens första lag , förutom med medelvärdestecken på några av storheterna:

$d\langle E\rangle =TdS+\mu _{1}d\langle N_{1}\rangle \ldots +\mu _{s}d\langle N_{s}\rangle -\langle p\rangle dV.$

Termodynamiska fluktuationer : Varianserna i energi och partikelantal är

$_ langle E^{2}\rangle -\langle E\rangle ^{2}=kT^{2}{\frac {\partial \langle E\rangle }{\partial T}}+kT\mu _{1} {\frac {\partial \langle E\rangle }{\partial \mu _{1}}}+kT\mu _{2}{\frac {\partial \langle E\rangle }{\partial \mu _{ 2}}}+\ldots ,}$

$\langle N_{1}^{2}\rangle -\langle N_{1}\rangle ^{2}=kT{\frac {\partial \langle N_{1}\rangle }{\partial \mu _{1}}}.$

Korrelationer i fluktuationer : Kovarianserna för partikelantal och energi är

$\langle N_{1}N_{2}\rangle -\langle N_{1}\rangle \langle N_{2}\rangle =kT{\frac {\partial \langle N_{2}\rangle }{ \partial \mu _{1}}}=kT{\frac {\partial \langle N_{1}\rangle }{\partial \mu _{2}}}.$

$\langle N_{1}E\rangle -\langle N_{1}\rangle \langle E\rangle =kT{\frac {\partial \langle E\rangle }{\partial \mu _{1}}},$

Exempel på ensembler

Användbarheten av den stora kanoniska ensemblen illustreras i exemplen nedan. I varje fall beräknas den stora potentialen på basis av förhållandet

$\Omega =-kT\ln \left(\sum _{\text{mikrostater}}e^{\frac {\mu NE }{kT}}\right)$

vilket krävs för att mikrostaternas sannolikheter ska summera till 1.

Statistik över icke-interagerande partiklar

Bosoner och fermioner (kvantum)

I det speciella fallet med ett kvantsystem av många icke-interagerande partiklar är termodynamiken enkel att beräkna. Eftersom partiklarna inte interagerar kan man beräkna en serie stationära tillstånd med en partikel, som var och en representerar en separerbar del som kan inkluderas i systemets totala kvanttillstånd. Låt oss nu hänvisa till dessa stationära enpartikeltillstånd som orbitaler (för att undvika att förväxla dessa "tillstånd" med det totala mångakroppstillståndet), med förutsättningen att varje möjlig inre partikelegenskap ( spin eller polarisation ) räknas som en separat orbital . Varje orbital kan vara upptagen av en partikel (eller partiklar), eller kan vara tom.

Eftersom partiklarna inte interagerar kan vi anta att varje orbital bildar ett separat termodynamiskt system . Således är varje orbital en storslagen kanonisk ensemble för sig själv, en så enkel att dess statistik omedelbart kan härledas här. Med fokus på bara en orbital märkt i ϵi _{, kommer} Nϵi _den totala energin för ett mikrotillstånd av N partiklar i denna orbital att vara , där är den karakteristiska energinivån för den orbitalen. Den stora potentialen för orbitalen ges av en av två former, beroende på om orbitalen är bosonisk eller fermionisk:

• För fermioner tillåter Paulis uteslutningsprincip endast två mikrotillstånd för orbitalen (ockupation av 0 eller 1), vilket ger en tvåtermsserie

  ${\begin{aligned}\Omega _{i}&=-kT\ln {\Big (}\summa _{N= 0}^{1}e^{\frac {N\mu -N\epsilon _{i}}{kT}}{\Big )}\\&=-kT\ln {\Big (}1+e^ {\frac {\mu -\epsilon _{i}}{kT}}{\Big )}\end{aligned}}$

• För bosoner kan N vara vilket icke-negativt heltal som helst och varje värde på N räknas som ett mikrotillstånd på grund av att partiklarna inte kan urskiljas , vilket leder till en geometrisk serie :
  ${\begin{aligned}\Omega _{i}&=-kT\ln {\Big (}\summa _{N=0}^{\infty }e^{\frac {N\mu -N \epsilon _{i}}{kT}}{\Big )}\\&=+kT\ln {\Big (}1-e^{\frac {\mu -\epsilon _{i}}{kT} }{\Big )}.\end{aligned}}$

I varje fall värdet $\scriptstyle \langle N_{i}\rangle =-{\tfrac {\partial \Omega _{i}}{\partial \mu } }$ ger det termodynamiska genomsnittliga antalet partiklar på orbitalen: Fermi–Dirac-fördelningen för fermioner och Bose–Einstein-fördelningen för bosoner. Om man återigen betraktar hela systemet, hittas den totala stora potentialen genom att addera Ω _i för alla orbitaler.

Oskiljbara klassiska partiklar

Inom klassisk mekanik är det också möjligt att överväga oskiljbara partiklar (i själva verket är oskiljbarhet en förutsättning för att definiera en kemisk potential på ett konsekvent sätt; alla partiklar av ett givet slag måste vara utbytbara). Vi överväger återigen att placera flera partiklar av samma slag i samma mikrotillstånd av enpartikelfasutrymme, som vi återigen kallar en "orbital". Men jämfört med kvantmekaniken kompliceras det klassiska fallet av det faktum att ett mikrotillstånd i klassisk mekanik inte hänvisar till en enda punkt i fasrymden utan snarare till en utökad region i fasrymden: ett mikrotillstånd innehåller ett oändligt antal tillstånd, alla distinkta men av liknande karaktär. Som ett resultat, när flera partiklar placeras i samma orbital, räknas inte den totala samlingen av partiklarna (i systemfasutrymmet) som ett helt mikrotillstånd utan snarare bara en bråkdel av ett mikrotillstånd, eftersom identiska tillstånd (bildade genom permutation ) identiska partiklar) bör inte överräknas. Överräkningskorrigeringsfaktorn är faktorn för antalet partiklar.

Statistiken i detta fall har formen av en exponentiell potensserie

${\begin{aligned}\Omega _{\rm {orb}}&=-kT\ln {\Big (}\summa _{N=0} ^{\infty }{\frac {1}{N!}}e^{\frac {N\mu -N\epsilon _{\rm {orb}}}{kT}}{\Big )}\\& =-kT\ln {\Big (}e^{e^{\frac {\mu -\epsilon _{\rm {orb}}}{kT}}}{\Big )}\\&=-kTe^ {\frac {\mu -\epsilon _{\rm {orb}}}{kT}},\end{aligned}}$

värdet $\scriptstyle \langle N_{\rm {orb}}\rangle =-{\tfrac {\partial \Omega _{\rm {orb }}}{\partial \mu }}$ motsvarande Maxwell–Boltzmanns statistik .

Jonisering av en isolerad atom

Ytjoniseringseffekt i en förångad cesiumatom vid 1500 K, beräknad med metoden i detta avsnitt (inklusive degeneration ). Y-axel: genomsnittligt antal elektroner; atomen är neutral när den har 55 elektroner. X-axel: energivariabel, som är lika med ytarbetsfunktionen .

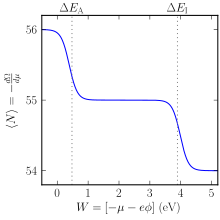
Den stora kanoniska ensemblen kan användas för att förutsäga om en atom föredrar att vara i neutralt tillstånd eller joniserat tillstånd. En atom kan existera i joniserade tillstånd med fler eller färre elektroner jämfört med neutrala. Som visas nedan kan joniserade tillstånd vara termodynamiskt föredragna beroende på miljön. Tänk på en förenklad modell där atomen kan vara i ett neutralt tillstånd eller i ett av två joniserade tillstånd (en detaljerad beräkning inkluderar även tillståndens degenerationsfaktorer):

• laddningsneutralt tillstånd, med N ₀ elektroner och energi E ₀ .
• ett oxiderat tillstånd ( ₀ N − 1 elektroner) med energi ₀ E + Δ E _I + qϕ
• ett reducerat tillstånd ( ₀ N + 1 elektroner) med energi ₀ E − Δ E _A − qϕ

Här är Δ E _I och Δ E _A atomens joniseringsenergi respektive elektronaffinitet ; ϕ är den lokala elektrostatiska potentialen i vakuumet nära atomen, och − q är elektronladdningen .

Den stora potentialen i detta fall bestäms alltså av

${\begin{aligned}\Omega &=-kT\ln {\Big (}e^{\frac {\mu N_{0}-E_{0}}{kT}}+e^{\frac {\mu N_{0}-\mu -E_{0}-\Delta E_{\rm {I}}-q\phi }{kT}}+e^{\frac {\mu N_{0}+\ mu -E_{0}+\Delta E_{\rm {A}}+q\phi }{kT}}{\Big )}.\\&=E_{0}-\mu N_{0}-kT\ ln {\Big (}1+e^{\frac {-\mu -\Delta E_{\rm {I}}-q\phi }{kT}}+e^{\frac {\mu +\Delta E_ {\rm {A}}+q\phi }{kT}}{\Big )}.\\\end{aligned}}$

Kvantiteten − qϕ − µ är kritisk i detta fall för att bestämma balansen mellan de olika tillstånden. Detta värde bestäms av miljön runt atomen.

Om en av dessa atomer placeras i en vakuumlåda, då är − qϕ − µ = W , lådans fodermaterials arbetsfunktion . Genom att jämföra tabellerna över arbetsfunktioner för olika fasta material med tabellerna för elektronaffinitet och joniseringsenergi för atomarter, är det tydligt att många kombinationer skulle resultera i en neutral atom, men vissa specifika kombinationer skulle resultera i att atomen föredrar ett joniserat tillstånd: t.ex. en halogenatom i en ytterbiumlåda eller en cesiumatom i en volframlåda . Vid rumstemperatur är denna situation inte stabil eftersom atomen tenderar att adsorbera till lådans exponerade foder istället för att flyta fritt. Vid höga temperaturer förångas emellertid atomerna från ytan i jonform; denna spontana ytjoniseringseffekt har använts som en cesiumjonkälla .

Vid rumstemperatur finner detta exempel tillämpning i halvledare , där joniseringen av en dopningsatom beskrivs väl av denna ensemble. I halvledaren ledningsbandkanten ϵ _C rollen som vakuumenerginivån (ersätter − qϕ ) , och µ är känd som Fermi-nivån . Naturligtvis är joniseringsenergin och elektronaffiniteten för dopningsatomen starkt modifierad i förhållande till deras vakuumvärden. Ett typiskt donatordopmedel i kisel, fosfor, har AE I ₌ 45 meV ; värdet på _. ϵC − µ i det inre kislet är initialt cirka 600 meV , vilket garanterar joniseringen av dopningsmedlet Värdet på ϵ _C − µ beror dock starkt på elektrostatik, så under vissa omständigheter är det möjligt att avjonisera dopningsmedlet.

Betydelse av kemisk potential, generaliserat "partikelantal"

Se även: Kemisk potential

För att ett partikelantal ska ha en tillhörande kemisk potential måste det bevaras under systemets interna dynamik, och endast kunna förändras när systemet byter ut partiklar med en extern reservoar.

Om partiklarna kan skapas av energi under systemets dynamik, får inte en associerad µN- term förekomma i sannolikhetsuttrycket för den stora kanoniska ensemblen. I själva verket är detta detsamma som att kräva att µ = 0 för den typen av partikel. Så är fallet för fotoner i en svart hålighet , vars antal ändras regelbundet på grund av absorption och emission på hålrummets väggar. (Å andra sidan kan fotoner i en mycket reflekterande kavitet bevaras och få en icke-noll µ .)

I vissa fall är antalet partiklar inte konserverat och N representerar en mer abstrakt konserverad kvantitet:

• Kemiska reaktioner : Kemiska reaktioner kan omvandla en typ av molekyl till en annan; om reaktioner inträffar N _i definieras så att de inte förändras under den kemiska reaktionen.
• Högenergipartikelfysik : Vanliga partiklar kan skapas ur ren energi, om en motsvarande antipartikel skapas. Om den här typen av process tillåts, så bevaras varken antalet partiklar eller antipartiklar. Istället N = (partikelantal - antipartikelantal) bevarad. När partikelenergierna ökar, finns det fler möjligheter att omvandla mellan partikeltyper, och så det finns färre antal som verkligen bevaras. Vid de allra högsta energierna är de enda bevarade talen elektrisk laddning , svagt isospin och baryontal - leptontal .

Å andra sidan, i vissa fall kan en enda sorts partikel ha flera bevarade nummer:

• Slutna fack : I ett system som består av flera fack som delar energi men inte delar partiklar, är det möjligt att ställa in de kemiska potentialerna separat för varje fack. Till exempel är en kondensator sammansatt av två isolerade ledare och laddas genom att applicera en skillnad i elektronkemisk potential .
• Långsam jämvikt : I vissa kvasi-jämviktssituationer är det möjligt att ha två distinkta populationer av samma sorts partikel på samma plats, som var och en är i jämvikt internt men inte med varandra. Även om det inte är strikt i jämvikt, kan det vara användbart att namnge kvasi-jämviktskemiska potentialer som kan skilja sig åt mellan de olika populationerna. Exempel: ( halvledarfysik ) distinkta kvasi-Fermi-nivåer (elektronkemiska potentialer) i ledningsbandet och valensbandet ; ( spintronik ) distinkta spin-up och spin-down kemiska potentialer; ( kryogenik ) distinkta paraväte- och ortovätekemiska potentialer.

Exakta uttryck för ensemblen

Det exakta matematiska uttrycket för statistiska ensembler har en distinkt form beroende på vilken typ av mekanik som övervägs (kvant eller klassisk), eftersom begreppet "mikrostat" är avsevärt annorlunda. Inom kvantmekaniken ger den stora kanoniska ensemblen en enkel beskrivning eftersom diagonalisering ger en uppsättning distinkta mikrotillstånd i ett system, var och en med väldefinierad energi och partikelantal. Det klassiska mekaniska fallet är mer komplext eftersom det inte involverar stationära tillstånd utan istället ett integrerat över kanoniskt fasutrymme .

Kvantmekanisk

Ytterligare information om representation av ensembler i kvantmekanik: Statistisk ensemble (matematisk fysik)

En statistisk ensemble inom kvantmekaniken representeras av en densitetsmatris , betecknad med ${\hat {\rho }}$ . Den stora kanoniska ensemblen är densitetsmatrisen

${\hat {\rho }}=\exp {\big (} {\tfrac {1}{kT}}(\Omega +\mu _{1}{\hat {N}}_{1}+\ldots +\mu _{s}{\hat {N}}_{ s}-{\hat {H}}){\big )},$

där Ĥ är systemets totala energioperatör ( Hamiltonian ), N̂ ₁ är systemets totala partikelantalsoperator för partiklar av typ 1, N̂ ₂ är totala partikelantaloperatören för partiklar av typ 2, och så vidare. exp är matrisexponentialoperatorn . Storpotentialen Ω bestäms av sannolikhetsnormaliseringsvillkoret att densitetsmatrisen har ett spår av ett, $Tr{\hat {\rho }}=1$ :

$e^{-{\frac {\Omega }{kT}}}=\operatörsnamn {Tr} \exp {\big (}{\tfrac {1}{kT}}(\mu _{1}{ \hat {N}}_{1}+\ldots +\mu _{s}{\hat {N}}_{s}-{\hat {H}}){\big )}.$

Observera att för den stora ensemblen är bastillstånden för operatorerna Ĥ , N̂ ₁ , etc. alla tillstånd med flera partiklar i Fock space , och densitetsmatrisen definieras på samma grund. Eftersom energi- och partikelantal alla bevaras separat, pendlar dessa operatörer ömsesidigt.

Den stora kanoniska ensemblen kan alternativt skrivas i en enkel form med bra–ket-notation , eftersom det är möjligt (med tanke på energi- och partikelnummeroperatorernas ömsesidigt pendlande karaktär) att hitta en komplett bas av samtidiga egentillstånd | ψ _i ⟩ , indexerad med i , där Ĥ | ψ _i ⟩ = E _i | ψ _i ⟩ , N̂ ₁ | ψ _i ⟩ = N _{1, i} | ψ _i ⟩ , och så vidare. Med tanke på en sådan egenbas är den stora kanoniska ensemblen helt enkelt

${\hat {\rho }}=\sum _{i}e^{\frac {\Omega +\mu _{1}N_{1,i}+\ldots +\mu _{s}N_ {s,i}-E_{i}}{kT}}|\psi _{i}\rangle \langle \psi _{i}|$

$e^{-{\frac {\Omega }{kT}}}=\sum _{i}e^{\frac {\mu _{1}N_{1,i}+\ldots +\mu _{s}N_{s,i}-E_{i}}{kT}}.$

där summan är över hela uppsättningen av tillstånd där tillstånd i har E _i total energi, N _{1, i} partiklar av typ 1, N _{2, i} partiklar av typ 2, och så vidare.

Klassisk mekanisk

Ytterligare information om representation av ensembler i klassisk mekanik: Statistisk ensemble (matematisk fysik)

Inom klassisk mekanik representeras en stor ensemble istället av en gemensam sannolikhetstäthetsfunktion definierad över flera fasutrymmen av varierande dimensioner, ρ ( N ₁ , … N _s , p ₁ , … p _n , q ₁ , … q _n ) , där p ) ₁ , … p _n och q ₁ , … q _n är de kanoniska koordinaterna (generaliserade momenta och generaliserade koordinater för systemets interna frihetsgrader. Uttrycket för den stora kanoniska ensemblen är något känsligare än den kanoniska ensemblen eftersom:

• Antalet partiklar och därmed antalet koordinater n varierar mellan de olika fasutrymmena, och,
• det är viktigt att överväga om permutering av liknande partiklar räknas som ett distinkt tillstånd eller inte.

I ett system av partiklar beror antalet frihetsgrader n på antalet partiklar på ett sätt som beror på den fysiska situationen. Till exempel, i en tredimensionell gas av monoatomer n = 3 N , men i molekylära gaser kommer det också att finnas rotations- och vibrationsfrihetsgrader.

Sannolikhetstäthetsfunktionen för den stora kanoniska ensemblen är:

$\rho ={\frac {1}{h^{n}C}}e^{\ frac {\Omega +\mu _{1}N_{1}+\ldots +\mu _{s}N_{s}-E}{kT}},$

var

• E är systemets energi, en funktion av fasen ( N ₁ , … N _s , p ₁ , … p _n , q ₁ , … q _n ) ,
• h är en godtycklig men förutbestämd konstant med enheterna energi×tid , som anger omfattningen av ett mikrotillstånd och ger korrekta dimensioner till ρ .
• C är en överräkningskorrigeringsfaktor (se nedan), en funktion av N ₁ , … N _s .

bestäms värdet av Ω genom att kräva att ρ är en normaliserad sannolikhetstäthetsfunktion:

$e^{-{\frac {\Omega }{kT}}}=\sum _{N_{1}=0}^{\infty }\ldots \sum _{N_{s}=0}^{\infty }\int \ldots \int {\frac {1}{h^{n}C}}e^{\frac {\mu _{1}N_{1}+\ldots +\mu _{s}N_{ s}-E}{kT}}\,dp_{1}\ldots dq_{n}$

Denna integral tar över hela det tillgängliga fasutrymmet för det givna antalet partiklar.

Överräkningskorrigering

Ytterligare information om överräkning av fasrum: Statistisk ensemble (matematisk fysik)

Ett välkänt problem inom den statistiska mekaniken för vätskor (gaser, vätskor, plasma) är hur man behandlar partiklar som är lika eller identiska till sin natur: ska de betraktas som särskiljbara eller inte? I systemets rörelseekvation spåras varje partikel för alltid som en särskiljbar enhet, och ändå finns det också giltiga tillstånd i systemet där positionerna för varje partikel helt enkelt har bytts: dessa tillstånd representeras på olika platser i fasrymden, men skulle ändå verkar vara likvärdiga.

Om permutationerna av liknande partiklar anses räknas som distinkta tillstånd, så är faktorn C ovan helt enkelt C = 1 . Ur denna synvinkel inkluderar ensembler varje permuterat tillstånd som ett separat mikrotillstånd. Även om det verkar godartat till en början, leder detta till ett problem med allvarligt icke-extensiv entropi i den kanoniska ensemblen, idag känd som Gibbs paradox . I den stora kanoniska ensemblen uppstår ytterligare en logisk inkonsekvens: antalet urskiljbara permutationer beror inte bara på hur många partiklar som finns i systemet, utan också på hur många partiklar som finns i reservoaren (eftersom systemet kan byta ut partiklar med en reservoar). I detta fall är entropin och den kemiska potentialen icke omfattande men också dåligt definierade, beroende på en parameter (reservoarstorlek) som borde vara irrelevant.

För att lösa dessa problem är det nödvändigt att utbytet av två liknande partiklar (inom systemet, eller mellan systemet och reservoaren) inte får anses ge ett distinkt tillstånd av systemet. För att införliva detta faktum bärs integraler fortfarande över hela fasutrymmet men resultatet divideras med

$C=N_{1}!N_{2}!\ldots N_{s}!,$

vilket är antalet möjliga olika permutationer. Divisionen med C korrigerar prydligt den överräkning som sker i integralen över hela fasutrymmet.

Det är naturligtvis möjligt att inkludera särskiljbara typer av partiklar i den stora kanoniska ensemblen – varje särskiljbar typ $i$ spåras av en separat partikelräknare $N_{i}$ och kemisk potential ${\ displaystyle \mu _{i}}$ . Som ett resultat är det enda konsekventa sättet att inkludera "fullständigt urskiljbara" partiklar i den stora kanoniska ensemblen att överväga alla möjliga urskiljbara typer av dessa partiklar, och att spåra varje möjlig typ med en separat partikelräknare och separat kemisk potential.