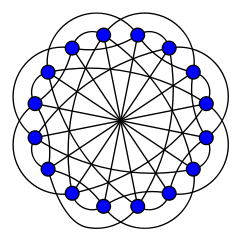
Clebsch graf

Clebsch graf
Clebsch graf
Döpt efter	Alfred Clebsch
Vertices	16
Kanter	40
Radie	2
Diameter	2
Omkrets	4
Automorfismer	1920
Kromatiskt nummer	4
Kromatiskt index	5
Boktjocklek	4
Könummer	3
Egenskaper	; ; ; ; ; Starkt regelbunden Hamiltonian Cayley-graf Vertex-transitive Edge-transitive Distance-transitive .
	Tabell över grafer och parametrar

Inom det matematiska området grafteori är Clebsch -grafen endera av två komplementära grafer på 16 hörn, en 5- regelbunden graf med 40 kanter och en 10-regelbunden graf med 80 kanter. 80-kantsgrafen är den halverade kubgrafen med dimension 5 ; det kallades Clebsch-grafnamnet av Seidel (1968) på grund av dess förhållande till konfigurationen av 16 linjer på den kvartsyta som upptäcktes 1868 av den tyske matematikern Alfred Clebsch . 40-kantsvarianten är dimensionen-5 vikta kubgrafen ; den är också känd som Greenwood–Gleason-grafen efter arbeten av Robert E. Greenwood och Andrew M. Gleason ( 1955 ), som använde den för att utvärdera Ramsey-talet R (3,3,3) = 17.

Konstruktion

Den dimension-5 vikta kubgrafen (den 5-regelbundna Clebsch-grafen) kan konstrueras genom att lägga till kanter mellan motsatta par av hörn i en 4-dimensionell hyperkubgraf. (I en n -dimensionell hyperkub är ett par hörn motsatta om den kortaste vägen mellan dem har n kanter.) Alternativt kan den bildas från en 5-dimensionell hyperkubgraf genom att identifiera (eller dra ihop) varje motsatt par av hörn. .

En annan konstruktion, som leder till samma graf, är att skapa en vertex för varje element i det finita fältet GF(16), och koppla två hörn med en kant närhelst skillnaden mellan motsvarande två fältelement är en perfekt kub .

Dimension-5 halverade kubgrafen (den 10-regelbundna Clebsch-grafen) är komplementet till den 5-regelbundna grafen. Den kan också konstrueras från hörn av en 5-dimensionell hyperkub, genom att koppla ihop par av hörn vars Hamming-avstånd är exakt två. Denna konstruktion är ett exempel på konstruktionen av Frankl–Rödl-grafer . Den producerar två delmängder av 16 hörn som är bortkopplade från varandra; båda dessa halvkvadrater av hyperkuben är isomorfa till den 10-regelbundna Clebsch-grafen. Två kopior av den 5-regelbundna Clebsch-grafen kan produceras på samma sätt från en 5-dimensionell hyperkub, genom att koppla ihop par av hörn vars Hamming-avstånd är exakt fyra.

Egenskaper

Den 5-regelbundna Clebsch-grafen är en starkt regelbunden graf av grad 5 med parametrar $(v,k,\lambda ,\mu )=( 16,5,0,2)$ . Dess komplement, den 10-regelbundna Clebsch-grafen, är därför också en starkt regelbunden graf, med parametrar $(16,10,6,6)$ .

Den 5-regelbundna Clebsch-grafen är hamiltonisk , icke-plan och icke-eulerisk . Den är också både 5- kant-ansluten och 5- kant-ansluten . Subgrafen som induceras av de tio icke-grannarna till någon vertex i denna graf bildar en isomorf kopia av Petersen-grafen .

Den har boktjocklek 4 och kö nummer 3.

K ₁₆ 3-färgad som tre Clebsch-grafer.

Kanterna på den kompletta grafen K ₁₆ kan delas upp i tre osammanhängande kopior av den 5-regelbundna Clebsch-grafen. Eftersom Clebsch-grafen är en triangelfri graf visar detta att det finns en triangelfri trefärgning av kanterna på K ₁₆ ; det vill säga att Ramsey-talet R (3,3,3) som beskriver det minsta antalet hörn i en komplett graf utan en triangelfri trefärgning är minst 17. Greenwood & Gleason (1955) använde denna konstruktion som en del av deras bevis på att R (3,3,3) = 17.

Den 5-regelbundna Clebsch-grafen kan färgas med fyra färger, men inte tre: dess största oberoende uppsättning har fem hörn, inte tillräckligt för att dela upp grafen i tre oberoende färgklasser. Den innehåller som en inducerad subgraf Grötzsch -grafen , den minsta triangelfria fyrkromatiska grafen, och varje fyrkromatisk inducerad subgraf i Clebsch-grafen är en supergraf av Grötzsch-grafen. Mer starkt är att varje triangelfri fyrkromatisk graf utan inducerad väg med längd sex eller mer är en inducerad subgraf av Clebsch-grafen och en inducerad supergraf av Grötzsch-grafen.

Den 5-regelbundna Clebsch-grafen är Keller-grafen av dimension två, en del av en familj av grafer som används för att hitta plattsättningar av högdimensionella euklidiska utrymmen av hyperkuber varav inte två möts ansikte mot ansikte.

Den 5-regelbundna Clebsch-grafen kan bäddas in som en vanlig karta i det orienterbara grenröret av släkte 5, och bildar femkantiga ytor; och i den icke-orienterbara ytan av släkte 6, bildande tetragonala ytor.

Algebraiska egenskaper

Det karakteristiska polynomet för den 5-regelbundna Clebsch-grafen är $(x+3)^{5}(x-1)^{10}( x-5)$ . Eftersom detta polynom helt kan faktoriseras i linjära termer med heltalskoefficienter, är Clebsch-grafen en integralgraf : dess spektrum består helt av heltal. Clebsch-grafen är den enda grafen med detta karakteristiska polynom, vilket gör det till en graf som bestäms av dess spektrum.

Den 5-regelbundna Clebsch-grafen är en Cayley-graf med en automorfismgrupp av ordningen 1920, isomorf till Coxeter-gruppen $D_{5}$ . Som en Cayley-graf verkar dess automorfismgrupp transitivt på sina hörn, vilket gör den transitiv vinkel . I själva verket är det bågtransitivt , därav kanttransitivt och avståndstransitivt . Den är också kopplad-homogen , vilket betyder att varje isomorfism mellan två anslutna inducerade subgrafer kan utökas till en automorfism av hela grafen.

Galleri

Clebsch-grafen är Hamiltonsk .
Det akromatiska numret på Clebsch-grafen är 8.
Det kromatiska numret på Clebsch-grafen är 4.
Det kromatiska indexet för Clebsch-grafen är 5.
Konstruktion av Clebsch-grafen från en hyperkubgraf .