Youngs ojämlikhet för produkter

Inom matematik är Youngs ojämlikhet för produkter en matematisk ojämlikhet om produkten av två tal . Ojämlikheten är uppkallad efter William Henry Young och bör inte förväxlas med Youngs faltningsojämlikhet .

Youngs ojämlikhet för produkter kan användas för att bevisa Hölders ojämlikhet . Det används också i stor utsträckning för att uppskatta normen för icke-linjära termer i PDE-teorin , eftersom det tillåter en att uppskatta en produkt av två termer med summan av samma termer upphöjd till en potens och skalad.

Standardversion för konjugerade Hölder-exponenter

Standardformen för ojämlikheten är följande:

Teorem — Om $a\geq 0$ och $b\geq 0$ är icke-negativa reella tal och om $p>1$ och $q>1$ är reella tal så att ${\frac {1}{p}}+{\frac {1}{q}}=1,$ sedan

$$ab~\leq ~{\frac {a^{p}}{p}}+{\frac {b^{q}}{q}}.$$

Likhet gäller om och endast om $a^{p}=b^{q}.$

Det kan användas för att bevisa Hölders ojämlikhet .

Bevis

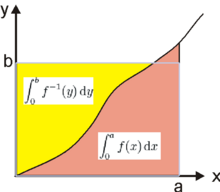
Eftersom ${\tfrac {1}{p}}+{\tfrac {1}{q}}=1,$$p-1={\tfrac {1}{q-1}}.$ En graf $y=x^{p-1}$ på $xy$ -planet är alltså också en graf $x=y^{q-1}.$ Det är intuitivt tydligt genom att skissa en visuell representation av integralerna av området mellan denna kurva och axlarna, och området i rektangeln som begränsas av linjerna $x=0,x=a,y=0,y=b,$ och det faktum att $y$ alltid ökar för att öka $x$ och vice versa, att följande olikhet för godtycklig $a,b\geq 0\in \mathbb {R}$ rymmer: $\int _{0}^{a}x^{p-1}\mathrm {d} x+\int _{0}^{b}y^{q-1}\mathrm {d} y\ geq ab.$ Youngs ojämlikhet följer av att utvärdera integralerna. (Se nedan .)

Denna form av Youngs ojämlikhet kan också bevisas via Jensens ojämlikhet .

Bevis

Påståendet är säkert sant om $a=0$ eller $b=0$ så antag hädanefter att $a>0$ och $b>0.$ Sätt $t=1/p$ och $(1-t)=1/q.$ Eftersom logaritmfunktionen är konkav ,

$$\ln \left(ta^{p}+(1-t)b^{q}\right)~\geq ~t\ln \left(a^{p}\right)+(1- t)\ln \left(b^{q}\right)=\ln(a)+\ln(b)=\ln(ab)$$

med jämställdheten om och endast om $a^{p}=b^{q}.$ Youngs ojämlikhet följer av exponentiering.

Youngs ojämlikhet kan likväl skrivas som

$$a^{\alpha }b^{\beta }\leq \alpha a+\beta b,\qquad \,0\leq \alpha ,\beta \leq 1,\quad \ \alpha +\beta =1.$$

logaritmfunktionens konkavitet . Likhet gäller om och endast om $a=b$ eller $\{\alpha ,\beta \}=\{0,1\}.$

Generaliseringar

Teorem — Antag att $a>0$ och $b>0.$ Om $1<p<\infty$ och $q$ är sådana att ${\tfrac {1}{p}}+{\tfrac {1}{q}}=1$ då

$$ab~=~\min _{0<t<\infty }\left({\frac {t^{p}a^{p}}{p}}+{\frac {t^{-q }b^{q}}{q}}\höger).$$

Använder $t:=1$ och ersätter $a$ med $a^{1/p}$ och $b$ med ${ \displaystyle b^{1/q}}$ resulterar i olikheten:

$$a^{1/p}\,b^{1/q}~\leq ~{\frac {a}{p}}+{ \frac {b}{q}},$$

vilket är användbart för att bevisa Hölders ojämlikhet .

Bevis

Definiera en verkligt värderad funktion $f$ på de positiva reella talen med

$$f(t)~=~{\frac {t^{p}a^{p}}{p}}+{\frac {t^{-q}b^{q}}{q}}$$

för varje $t>0$ och beräkna sedan dess minimum.

Teorem — Om $0\leq p_{i}\leq 1$ med $\sum _{i}p_{i}=1$ så

$$\prod _{i}{a_{i}}^{p_{i}}~\leq ~\sum _{i}p_{i}a_{i}.$$

Likhet gäller om och endast om alla $a_{i}$ s med icke-noll $p_{i}$ s är lika.

Elementärt fall

Ett elementärt fall av Youngs ojämlikhet är ojämlikheten med exponent $2,$

$$ab\leq {\frac {a^{2}}{2}}+{\frac {b^{2}}{2}},$$

vilket också ger upphov till den så kallade Youngs ojämlikhet med $\varepsilon$ (gäller för varje $\varepsilon >0$ ), ibland kallad Peter–Paul ojämlikheten. Detta namn syftar på det faktum att strängare kontroll av den andra termen uppnås till priset av att man förlorar viss kontroll över den första termen – man måste "råna Peter för att betala Paul"

$$ab~\leq ~{\frac {a^{2}}{2\varepsilon }}+{\frac {\varepsilon b^{2}}{2}}.$$

Bevis : Youngs olikhet med exponent $2$ är specialfallet $p=q=2.$ Det har dock ett mer elementärt bevis.

Börja med att observera att kvadraten på varje reellt tal är noll eller positivt. Därför kan vi för varje par reella tal $a$ och $b$ skriva:

$$0\leq (ab)^{2}$$

Räkna ut kvadraten på höger sida:

$$0\leq a^{2}-2ab+b^{2}$$

Lägg till $2ab$ på båda sidor:

$$2ab\leq a^{2}+b^{2}$$

Dividera båda sidor med 2 och vi har Youngs olikhet med exponent $2:$

$$ab\leq {\frac {a^{2}}{2}}+{\frac {b^{2}}{2}}$$

Youngs olikhet med $\varepsilon$ följer genom att ersätta $a'$ och $b'$ enligt nedan i Youngs olikhet med exponent $2:$

$$a'=a/{\sqrt {\varepsilon }},\;b'={\sqrt {\varepsilon }}b.$$

Matriell generalisering

T. Ando bevisade en generalisering av Youngs ojämlikhet för komplexa matriser ordnade efter Loewner-beställning . Den anger att för alla par $A,B$ av komplexa matriser av ordningen $n$ finns det en enhetlig matris $U$ så att

$$U^{*}|AB^{*}|U\preceq {\tfrac {1}{p}}|A|^{p}+{\tfrac {1}{q}}|B |^{q},$$

där ${}^{*}$ anger den konjugerade transponeringen av matrisen och $|A|={\sqrt {A^{*}A}}.$

Standardversion för utökade funktioner

Arean av rektangeln a,b får inte vara större än summan av ytorna under funktionerna $f$ (röd) och $f^{-1}$ (gul)

För standardversionen av olikheten, låt $f$ beteckna en reellt värderad, kontinuerlig och strikt ökande funktion på $[0,c]$ med $c>0$ och $f(0)=0.$ Låt $f^{-1}$ beteckna den inversa funktionen av $f.$ Sedan, för alla $a\in [0,c]$ och $b\in [0,f(c)],$

$$ab~\leq ~\int _{0}^{a}f(x)\,dx+\int _ {0}^{b}f^{-1}(x)\,dx$$

med likhet om och endast om $b=f(a).$

Med $f(x)=x^{p-1}$ och $f^{-1}(y )=y^{q-1},$ detta reduceras till standardversion för konjugerade Hölder-exponenter.

För detaljer och generaliseringar hänvisar vi till uppsatsen från Mitroi & Niculescu.

Generalisering med Fenchel–Legendre-transformers

Genom att beteckna det konvexa konjugatet av en reell funktion $f$ med $g,$ får vi

$$ab~\leq ~f(a)+g(b).$$

Detta följer omedelbart av definitionen av det konvexa konjugatet. För en konvex funktion $f$ följer detta också av Legendre-transformationen .

Mer allmänt, om $f$ är definierad på ett reellt vektorrum $X$ och dess konvexa konjugat betecknas med ${\displaystyle f^{\star }} ($ och definieras på det dubbla rummet $X^{\star }$ ), sedan

$$\langle u,v\rangle \leq f^{\star }(u)+f(v).$$

där ${\displaystyle \langle \cdot ,\cdot \rangle :X^{\star }\times X\to \mathbb {R} } är den$ dubbla parningen .

Exempel

Det konvexa konjugatet av $f(a)=a^{p}/p$ är $g(b)=b^{ q}/q$ med $q$ så att ${\tfrac {1}{p}}+{\tfrac {1}{q}}=1,$ och därmed är Youngs olikhet för konjugerade Hölder-exponenter som nämnts ovan ett specialfall.

Legendre-transformen av $f(a)=e^{a}-1$ är $g(b) =1-b+b\ln b$ , därav $ab\leq e^{a}-b+b\ln b$ för alla icke-negativa $a$ och $b.$ Denna uppskattning är användbar i teorin om stora avvikelser under exponentiella momentförhållanden, eftersom $b\ln b$ förekommer i definitionen av relativ entropi , som är hastighetsfunktionen i Sanovs sats .

Se även

• Konvex konjugat – den ("dubbel") lägre-semikontinuerliga konvexa funktionen som är ett resultat av Legendre–Fenchel-transformationen av en "primal" funktion Sidor som visar wikidata-beskrivningar som en reserv
• Integral av inversa funktioner – Matematisk sats, används i kalkyl
• Legendre transformation – Matematisk transformation
• Youngs veckojämlikhet

Anteckningar

•    Jarchow, Hans (1981). Lokalt konvexa utrymmen . Stuttgart: BG Teubner. ISBN 978-3-519-02224-4 . OCLC 8210342 .
•    Bahouri, Hajer ; Chemin, Jean-Yves ; Danchin, Raphaël (2011). Fourieranalys och ickelinjära partiella differentialekvationer . Grundlehren der mathematischen Wissenschaften. Vol. 343. Berlin, Heidelberg: Springer. ISBN 978-3-642-16830-7 . OCLC 704397128 .

externa länkar

• Youngs ojämlikhet på PlanetMath
• Weisstein, Eric W. "Ungs ojämlikhet" . MathWorld .