Jordens radie

För dess historiska utveckling, se Sfärisk jord . För dess bestämning, se Bågmätning .

Jordens radie
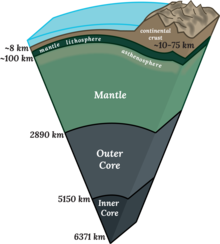Tvärsnitt av jordens inre
Allmän information
Enhetssystem	astronomi , geofysik
Enhet av	distans
Symbol	R 🜨 eller $R_{E}$ , ${\mathcal {R}}_{\mathrm {eE} }^{\mathrm {N} }$
Konverteringar
1 R 🜨 i...	... är lika med ...
SI basenhet	6,3781 × 10 6 m
Metriska systemet	6 357 till 6 378 km
engelska enheter	3 950 till 3 963 mi

Jordradien (betecknad som R _🜨 eller $R_{E}$ ) är avståndet från jordens centrum till en punkt på eller nära dess yta. När man approximerar jordens figur med en jordsfäroid sträcker sig radien från maximalt nästan 6 378 km (3 963 mi) ( ekvatorialradie , betecknad a ) till ett minimum av nästan 6 357 km (3 950 mi) ( polär radie , betecknad b ).

En nominell jordradie används ibland som en måttenhet inom astronomi och geofysik , vilket rekommenderas av International Astronomical Union för att vara ekvatorialvärdet.

Ett globalt medelvärde anses vanligtvis vara 6 371 kilometer (3 959 mi) med en variation på 0,3 % (±10 km) av följande skäl. International Union of Geodesy and Geophysics (IUGG) tillhandahåller tre referensvärden: medelradien (R ₁ ) för tre radier mätt vid två ekvatorpunkter och en pol; den ataliska radien , som är radien för en sfär med samma ytarea (R ₂ ); och den volymetriska radien , som är radien för en sfär som har samma volym som ellipsoiden (R ₃ ). Alla tre värden är cirka 6 371 kilometer (3 959 mi).

Andra sätt att definiera och mäta jordens radie involverar krökningsradien . Några få definitioner ger värden utanför intervallet mellan polarradie och ekvatorialradie eftersom de inkluderar lokal eller geoidal topografi eller för att de beror på abstrakta geometriska överväganden.

Introduktion

Ett skaldiagram av oblateness av 2003 IERS referensellipsoid , med norr överst. Det ljusblå området är en cirkel. Den yttre kanten av den mörkblå linjen är en ellips med samma mindre axel som cirkeln och samma excentricitet som jorden. Den röda linjen representerar Karman-linjen 100 km (62 mi) över havet , medan det gula området betecknar ISS :s höjdområde i låg jordomloppsbana .

Huvudartiklar: Jordens figur , Jordellipsoid och Referensellipsoid

Jordens rotation , interna densitetsvariationer och yttre tidvattenkrafter gör att dess form systematiskt avviker från en perfekt sfär. Lokal topografi ökar variansen, vilket resulterar i en yta av djup komplexitet. Våra beskrivningar av jordens yta måste vara enklare än verkligheten för att kunna hanteras. Därför skapar vi modeller för att approximera egenskaperna hos jordens yta, i allmänhet förlitar vi oss på den enklaste modellen som passar behovet.

Var och en av de vanliga modellerna involverar en uppfattning om den geometriska radien . Strängt taget är sfärer de enda fasta ämnen som har radier, men bredare användningar av termen radie är vanliga inom många områden, inklusive de som handlar om modeller av jorden. Följande är en ofullständig lista över modeller av jordens yta, sorterade från exakt till mer ungefärlig:

• Jordens faktiska yta
• Geoiden , definierad av medelhavsnivån vid varje punkt på den verkliga ytan
• En sfäroid , även kallad en rotationsellipsoid , geocentrisk för att modellera hela jorden, eller annars geodetisk för regionalt arbete
• En sfär

När det gäller geoiden och ellipsoiderna kallas det fasta avståndet från valfri punkt på modellen till det angivna centrumet "en radie av jorden" eller "jordens radie vid den punkten" . Det är också vanligt att referera till vilken medelradie som helst av en sfärisk modell som "jordens radie" . När man betraktar jordens verkliga yta är det å andra sidan ovanligt att hänvisa till en "radie", eftersom det i allmänhet inte finns något praktiskt behov. Snarare är höjd över eller under havsytan användbar.

Oavsett modell faller vilken radie som helst mellan det polära minimumet på cirka 6 357 km och det ekvatoriska maximumet på cirka 6 378 km (3 950 till 3 963 mi). Därför avviker jorden från en perfekt sfär med endast en tredjedel av en procent, vilket stöder den sfäriska modellen i de flesta sammanhang och motiverar termen "jordens radie". Även om specifika värderingar skiljer sig åt, generaliserar begreppen i den här artikeln till alla större planeter .

Fysik av jordens deformation

Rotation av en planet gör att den närmar sig en oblate ellipsoid /sfäroid med en utbuktning vid ekvatorn och tillplattad vid nord- och sydpolen , så att ekvatorialradien a är större än den polära radien b med ungefär aq . Oblathetskonstanten q ges av

$q={\frac {a^{3}\omega ^{2}}{GM}}\,,$

där ω är vinkelfrekvensen , G är gravitationskonstanten och M är planetens massa. För jorden 1 / q ≈ 289 , vilket är nära den uppmätta inversa utplattningen 1 / f ≈ 298,257 . Dessutom visar utbuktningen vid ekvatorn långsamma variationer. Utbuktningen hade minskat, men sedan 1998 har utbuktningen ökat, möjligen på grund av omfördelning av havsmassa via strömmar.

Variationen i densitet och jordskorpans tjocklek gör att gravitationen varierar över ytan och i tid, så att medelhavsnivån skiljer sig från ellipsoiden. Denna skillnad är geoidhöjden . , positiv över eller utanför ellipsoiden, negativ under eller inuti Geoidhöjdsvariationen är under 110 m (360 fot) på jorden. Geoidhöjden kan ändras abrupt på grund av jordbävningar (som jordbävningen på Sumatra-Andaman ) eller minskning av ismassorna (som Grönland ).

Alla deformationer har inte sitt ursprung i jorden. Gravitationsattraktion från månen eller solen kan göra att jordens yta vid en given punkt varierar med tiondels meter under en nästan 12-timmarsperiod (se jordens tidvatten ).

Radie och lokala förhållanden

Al-Birunis (973–1048) metod för beräkning av jordens radie förenklade mätningen av omkretsen jämfört med att ta mätningar från två platser långt från varandra.

Med tanke på lokal och övergående påverkan på ythöjden, är värdena som definieras nedan baserade på en "allmänt ändamål" modell, förfinad så globalt exakt som möjligt inom 5 m (16 fot) från referensellipsoidhöjden och till inom 100 m (330 fot) av medelhavsnivån (om man bortser från geoidhöjden).

Dessutom kan radien uppskattas från jordens krökning vid en punkt. Liksom en torus kommer krökningen vid en punkt att vara störst (snävare) i en riktning (nord–sydlig på jorden) och minsta (plattast) vinkelrätt (öst–väst). Motsvarande krökningsradie beror på platsen och riktningen för mätningen från den punkten. En konsekvens är att avståndet till den sanna horisonten vid ekvatorn är något kortare i nord–sydlig riktning än i öst–västlig riktning.

Sammanfattningsvis förhindrar lokala variationer i terrängen att definiera en enda "exakt" radie. Man kan bara anta en idealiserad modell. Sedan uppskattningen av Eratosthenes har många modeller skapats. Historiskt sett var dessa modeller baserade på regional topografi, vilket gav den bästa referensellipsoiden för det undersökta området. I takt med att satellitfjärranalys och speciellt Global Positioning System fick betydelse utvecklades sanna globala modeller som, även om de inte är lika exakta för regionalt arbete, bäst approximerar jorden som helhet.

Extrema: ekvatoriska och polära radier

Följande radier är härledda från World Geodetic System 1984 ( WGS-84 ) referensellipsoid . Det är en idealiserad yta, och de jordmått som används för att beräkna den har en osäkerhet på ±2 m i både ekvatorial- och polardimensionerna. Ytterligare avvikelser orsakade av topografisk variation på specifika platser kan vara betydande. När man identifierar positionen för en observerbar plats kan användningen av mer exakta värden för WGS-84-radier inte ge en motsvarande förbättring av noggrannheten .

Värdet för ekvatorialradien definieras till närmaste 0,1 m i WGS-84. Värdet för polradien i detta avsnitt har avrundats till närmaste 0,1 m, vilket förväntas vara tillräckligt för de flesta användningsområden. Se WGS-84-ellipsoiden om ett mer exakt värde för dess polära radie behövs.

• Jordens ekvatorialradie a , eller halvhuvudaxel , är avståndet från dess mitt till ekvatorn och motsvarar 6 378,1370 km (3 963,1906 mi). Ekvatorialradien används ofta för att jämföra jorden med andra planeter .

• Jordens polarradie b , eller semi-mindre axel , är avståndet från dess centrum till nord- och sydpolen och motsvarar 6 356,7523 km (3 949,9028 mi).

Platsberoende radier

Tre olika radier som en funktion av jordens latitud. R är den geocentriska radien; M är den meridionala krökningsradien; och N är den primära vertikala krökningsradien.

Geocentrisk radie

Ej att förväxla med geocentriskt avstånd .

Den geocentriska radien är avståndet från jordens centrum till en punkt på sfäroidytan vid geodetisk latitud φ :

$R(\varphi )={\sqrt { \frac {(a^{2}\cos \varphi )^{2}+(b^{2}\sin \varphi )^{2}}{(a\cos \varphi )^{2}+(b \sin \varphi )^{2}}}}$

där a och b är ekvatorialradien respektive den polära radien.

De extrema geocentriska radierna på ellipsoiden sammanfaller med de ekvatoriala och polära radierna. De är hörn av ellipsen och sammanfaller också med minsta och maximala krökningsradie.

Krökningsradier

Se även: Sfäroid § Krökning

Huvudkurvaturradier

Det finns två huvudsakliga krökningsradier : längs de meridionala och prime-vertikala normalsektionerna .

Meridional

I synnerhet är jordens meridionala krökningsradie (i nord–sydlig riktning) vid φ :

$M(\varphi )={\frac {(ab)^{2}}{{\big (}(a\cos \varphi )^{2}+(b\sin \varphi )^{2} {\big )}^{\frac {3}{2}}}}={\frac {a(1-e^{2})}{(1-e^{2}\sin ^{2}\ varphi )^{\frac {3}{2}}}}={\frac {1-e^{2}}{a^{2}}}N(\varphi )^{3}\,.$

där $e$ är jordens excentricitet . Detta är radien som Eratosthenes mätte i sin bågmätning .

Prime vertikalt

Längden PQ, som kallas den prime vertikala radien , är $N(\phi )$ . Längden IQ är lika med $\,e^{2}N(\phi )$ . $R=(X,\,Y,\,Z)$ .

Om en punkt hade dykt upp rakt öster om den andra, finner man den ungefärliga krökningen i öst–västlig riktning.

Denna jords primära-vertikala krökningsradie , även kallad jordens tvärgående krökningsradie , definieras vinkelrätt ( ortogonalt ) mot M vid geodetisk latitud φ är:

$N(\varphi )={\frac {a^{2}}{\sqrt {(a\cos \varphi )^{2}+(b\sin \varphi )^{2}}}}= {\frac {a}{\sqrt {1-e^{2}\sin ^{2}\varphi }}}\,.$

N kan också tolkas geometriskt som det normala avståndet från ellipsoidytan till polaxeln. Radien för en latitudparallell ges av $p=N\cos(\varphi )$ .

Polar och ekvatorial krökningsradie

Jordens meridionala krökningsradie vid ekvatorn är lika med meridianens semi-latus rektum :

   b ² / a = 6 335,439 km

Jordens prim-vertikala krökningsradie vid ekvatorn är lika med ekvatorialradien, N = a .

Jordens polära krökningsradie (antingen meridional eller prim-vertikal) är:

   a ² / b = 6 399,594 km

Härledning

Utökat innehåll

De huvudsakliga krökningarna är rötterna till ekvation (125) i: $(EG-F^{2 })\,\kappa ^{2}-(eG+gE-2fF)\,\kappa +(t.ex.-f^{2})=0=\det(A-\kappa \,B),$ där i den första grundformen för en yta (Ekvation (112) i): $ds^{2}=\sum _{ij}a_ {ij}dw^{i}dw^{j}=E\,d\varphi ^{2}+2F\,d\varphi \,d\lambda +G\,d\lambda ^{2},$ E, F och G är element i den metriska tensorn : $A=a_{ij}=\summa _{\nu }{\frac {\ partiell r^{\nu }}{\partial w^{i}}}{\frac {\partial r^{\nu}}{\partial w^{j}}}=\left[{\begin{array }{ll}E&F\\F&G\end{array}}\right],$ $r=[r^{1},r^{2},r^{3}]^{T} =[x,y,z]^{T}$ , $w^{1}=\varphi$ , $w^{2}=\lambda ,$ i den andra grundformen för en yta (Ekvation (123) i): $\displaystyle 2D=\sum _{ij}b_{ij}dw^ {i}dw^{j}=e\,d\varphi ^{2}+2f\,d\varphi \,d\lambda +g\,d\lambda ^{2},}$ e, f och g är element i formtensorn: $B=b_{ij}=\summa _{\nu }n^{\nu }{\frac {\partial ^{2}r^{\nu}}{\partial w^{i}\partial w^{j}}}=\left[{\begin{array}{ll}e&f\ \f&g\end{array}}\right],$ $n={\frac {N}{|N|}}$ är enheten vinkelrät mot ytan vid $r$ , och eftersom ${\frac {\partial r} {\partial \varphi }}$ och ${\frac {\partial r}{\partial \lambda }}$ är tangenter till ytan, $N={\frac {\partial r}{\partial \varphi }}\times {\frac {\partial r}{\partial \lambda }}$ är normal mot ytan vid $r$ . Med $F=f=0$ för en oblate sfäroid är krökningarna $\kappa _{1}={\frac {g}{G}}$ och $\kappa _{2}={\frac {e}{ E}}\,,$ och de huvudsakliga krökningsradierna är $R_{1}={\frac {1}{\kappa _{1}}}$ och $R_{2}={\frac {1}{\kappa _{2}}}.$ Den första och andra krökningsradien motsvarar jordens meridionala respektive prime-vertikala krökningsradier. Geometriskt ger den andra grundformen avståndet från $r+dr$ till planettangenten vid $r$ .

Kombinerade krökningsradier

Azimuthal

Jordens azimutala krökningsradie , längs en jordnormalsektion vid en azimut (mätt medurs från norr) α och vid latitud φ , härleds från Eulers krökningsformel enligt följande:

$R_{\mathrm {c} }={\frac {1}{{\dfrac {\cos ^{2}\alpha}{M}}+{\dfrac {\sin ^{2}\alpha } {N}}}}\,.$

Oriktad

Det är möjligt att kombinera de huvudsakliga krökningsradierna ovan på ett icke-riktat sätt.

Jordens : Gaussiska krökningsradie vid latitud φ är

$R_{\mathrm {a} }(\varphi )={\frac {1}{\sqrt {K}}}={\frac {1}{2\pi }}\int _{0}^ {2\pi }R_{\mathrm {c} }(\alpha )\,d\alpha \,={\sqrt {MN}}={\frac {a^{2}b}{(a\cos \ varphi )^{2}+(b\sin \varphi )^{2}}}={\frac {a{\sqrt {1-e^{2}}}}{1-e^{2}\sin ^{2}\varphi }}\,.$

Där K är den Gaussiska krökningen , $K=\kappa _{1}\,\kappa _{2}={\frac {\det \,B}{\ det \,A}}$ .

Jordens : genomsnittliga krökningsradie vid latitud φ är

$R_{\mathrm {m} }={\frac {2}{{\dfrac {1}{M}}+{\dfrac {1}{N}}} }\,\!$

Globala radier

Jorden kan modelleras som en sfär på många sätt. Det här avsnittet beskriver de vanliga sätten. De olika radierna som härleds här använder notationen och dimensionerna som noterats ovan för jorden som härleds från WGS-84 - ellipsoiden; nämligen,

Ekvatorialradie : a = ( 6 378 .1370 km )

Polarradie : b = ( 6 356 .7523 km )

En sfär som är en grov approximation av sfäroiden, som i sig är en approximation av geoiden, enheter anges här i kilometer snarare än den millimeterupplösning som är lämplig för geodesi.

Nominell radie

Inom astronomi betecknar International Astronomical Union den nominella ekvatoriala jordens radie som ${\displaystyle {\mathcal {R}}_{\mathrm {eE} }^{\mathrm {N} }} ,$ vilket definieras till vara 6 378,1 km (3 963,2 mi). Den nominella polära jordens radie definieras som ${\mathcal {R}}_{\mathrm {pE} }^{\mathrm {N} }$ = 6 356,8 km (3 949,9 mi). Dessa värden motsvarar jordens tidvatten noll konvent. Ekvatorialradien används konventionellt som det nominella värdet om inte den polära radien uttryckligen krävs. Den nominella radien fungerar som en längdenhet för astronomi . (Notationen är definierad så att den lätt kan generaliseras för andra planeter ; t.ex. ${\mathcal {R}}_{\mathrm {pJ} }^{\mathrm {N} }$ för den nominella polära Jupiterradien .)

Aritmetisk medelradie

Ekvatorial ( a ), polär ( b ) och aritmetisk medelvärde av jordradien enligt definitionen i 1984 års revision av World Geodetic System (ej skalenlig)

Inom geofysik definierar International Union of Geodesy and Geophysics (IUGG) jordens aritmetiska medelradie (betecknad R ₁ ) till att vara

$R_{1}={\frac {2a+b}{3}}\,\!$

Faktorn två står för den biaxiala symmetrin i jordens sfäroid, en specialisering av triaxial ellipsoid. För jorden är den aritmetiska medelradien 6 371,0088 km (3 958,7613 mi).

Autalisk radie

Se även: Autalisk breddgrad

Jordens ataliska radie (som betyder "lika område" ) är radien för en hypotetisk perfekt sfär som har samma yta som referensellipsoiden . IUGG R2 _den ataliska radien som . En lösning i sluten form finns för en sfäroid:

$R_{2}={\sqrt {\frac {a^{2}+{\frac {b^{2}}{e}}\ln {\left({\frac {1+e}{ b/a}}\right)}}{2}}}={\sqrt {{\frac {a^{2}}{2}}+{\frac {b^{2}}{2}}{ \frac {\tanh ^{-1}e}{e}}}}={\sqrt {\frac {A}{4\pi }}}\,,$

där e ² = a ² − b ² / a ² och A är sfäroidens ytarea.

För jorden är den ataliska radien 6 371,0072 km (3 958,7603 mi).

Den ataliska radien $R_{2}$ motsvarar också radien för (global) medelkurvatur , erhållen genom att medelvärdesberäkning av Gauss-kurvaturen, $K$ , över ellipsoidens yta. Med hjälp av Gauss-Bonnet-satsen ger detta

${\frac {\int K\,dA}{A}}={\frac {4\pi }{A}}={\frac {1}{R_{2}^{2}}}.$

Volumetrisk radie

En annan sfärisk modell definieras av jordens volymetriska radie , som är radien för en volymsfär som är lika med ellipsoiden. IUGG betecknar R3 _den volymetriska radien som .

$R_{3}={\sqrt[{3}]{a^{2}b}}\,.$

För jorden är den volymetriska radien lika med 6 371,0008 km (3 958,7564 mi).

Likriktarradie

Se även: Kvartsmeridian och Rectifying latitude

En annan global radie är jordens likriktande radie , vilket ger en sfär med omkrets lika med omkretsen av ellipsen som beskrivs av något polärt tvärsnitt av ellipsoiden. Detta kräver en elliptisk integral för att hitta, givet de polära och ekvatoriala radierna:

$M_{\mathrm {r} }={\frac {2}{\pi }}\int _{0}^{\frac {\pi }{2}}{\sqrt {{a^{2 }}\cos ^{2}\varphi +{b^{2}}\sin ^{2}\varphi }}\,d\varphi \,.$

Likriktarradien är ekvivalent med meridionalmedelvärdet, vilket definieras som medelvärdet av M :

$M_{\mathrm {r} }={\frac {2}{\pi }}\int _{0}^{\frac {\pi }{2}}\!M(\varphi )\, d\varphi \,.$

För integrationsgränser på [0, π / 2 ] utvärderas integralerna för likningsradie och medelradie till samma resultat, vilket för jorden uppgår till 6 367,4491 km (3 956,5494 mi).

Det meridionala medelvärdet är väl approximerat av det halvkubiska medelvärdet av de två axlarna, [

$M_{\mathrm {r} }\approx \left({\frac {a^{\frac {3}{2}}+b ^{\frac {3}{2}}}{2}}\right)^{\frac {2}{3}}\,,$

som skiljer sig från det exakta resultatet med mindre än 1 μm (4 × 10 ⁻⁵ tum); medelvärdet av de två axlarna,

$M_{\mathrm {r} }\approx {\frac {a+b}{2}}\,,$

cirka 6,367,445 km (3,956,547 mi), kan också användas.

Topografiska radier

Se även: Jord § Storlek och form

De matematiska uttrycken ovan gäller över ellipsoidens yta. Fallen nedan betraktar jordens topografi , över eller under en referensellipsoid . Som sådana är de topografiska geocentriska avstånd , R _t , som inte bara beror på latitud.

Topografiska ytterligheter

• Maximal R _t : toppen av Chimborazo är 6 384,4 km (3 967,1 mi) från jordens centrum.
• Minsta R _{t :} Norra ishavets botten är 6 352,8 km (3 947,4 mi) från jordens centrum.

Topografiskt globalt medelvärde

Det topografiska genomsnittliga geocentriska avståndet är genomsnittliga höjder överallt, vilket resulterar i ett värde som är 230 m större än IUGG-medelradien , den ataliska radien eller den volymetriska radien . Detta topografiska medelvärde är 6 371 230 km (3 958,899 mi) med en osäkerhet på 10 m (33 fot).

Härledda kvantiteter: diameter, omkrets, båglängd, area, volym

Jordens diameter är helt enkelt två gånger jordens radie; till exempel ekvatorialdiameter (2a ) och polärdiameter (2b ) . För WGS84-ellipsoiden är det respektive:

• 2a = 12 756,2740 km (7 926,3812 mi ) ,
• 2 b = 12 713,5046 km (7 899,8055 mi) .

Jordens omkrets är lika med omkretslängden . Den ekvatoriala omkretsen är helt enkelt cirkelns omkrets : C _e =2 πa , i termer av ekvatorialradien, a . Den polära omkretsen är lika med C _p =4 m _p , fyra gånger fjärdedels meridianen m _p = aE ( e ), där den polära radien b kommer in via excentriciteten, e ⁼ ( 1− b2 / a2 ) ^{0,5 ;} se Ellipse#Circumference för detaljer.

Båglängden av mer allmänt ytkurvor , liksom meridianbågar och geodesics , kan också härledas från jordens ekvatorial- och polära radier.

Likaså för yta , antingen baserat på en kartprojektion eller en geodetisk polygon .

Jordens volym , eller den för referensellipsoiden, är V = 4 / 3 π a ² b . Med hjälp av parametrarna från WGS84 rotationsellipsoid, a = 6 378,137 km och b = 6 356 ,752 3142 km , V = 1,08321 × 10 ¹² km ³ (2,5988 × 10 ¹¹ cu mi) .

Publicerade värden

Den här tabellen sammanfattar de accepterade värdena för jordens radie.

Byrå	Beskrivning	Värde (i meter)	Ref
IAU	nominell "noll tidvatten" ekvatorial	6 378 100
IAU	nominell "noll tidvatten" polar	6 356 800
IUGG	ekvatorialradie	6 378 137
IUGG	semiminoraxel ( b )	6 356 752 .3141
IUGG	polär krökningsradie ( c )	6 399 593 .6259
IUGG	medelradie ( R1 )	6 371 008 .7714
IUGG	sfärens radie på samma yta ( R2 )	6 371 007 .1810
IUGG	sfärens radie med samma volym ( R3 )	6 371 000 .7900
IERS	WGS-84 ellipsoid, halvstor axel ( a )	6 378 137 .0
IERS	WGS-84 ellipsoid, semi-mollaxel ( b )	6 356 752 .3142
IERS	WGS-84 ellipsoid, polär krökningsradie ( c )	6 399 593 .6258
IERS	WGS-84 ellipsoid, medelradie för halvaxlar ( R 1 )	6 371 008 .7714
IERS	WGS-84 ellipsoid, sfärens radie med lika yta ( R 2 )	6 371 007 .1809
IERS	WGS-84 ellipsoid, sfärens radie med lika volym ( R 3 )	6 371 000 .7900
	GRS 80 halvstor axel ( a )	6 378 137 .0
	GRS 80 semi-mollaxel ( b )	≈6 356 752 .314 140
	Sfärisk jord Ca. av radie ( R E )	6 366 707 .0195
	meridional krökningsradie vid ekvatorn	6 335 439
	Maximum (toppen av Chimborazo)	6 384 400
	Minimum (golvet i Ishavet)	6 352 800
	Genomsnittligt avstånd från centrum till ytan	6 371 230 ± 10

Historia

Huvudartikel: Geodesins historia

Den första publicerade hänvisningen till jordens storlek dök upp runt 350 f.Kr. , när Aristoteles rapporterade i sin bok On the Heavens att matematiker hade gissat att jordens omkrets var 400 000 stadia . Forskare har tolkat Aristoteles siffra att vara allt från mycket exakt till nästan dubbla det verkliga värdet. Den första kända vetenskapliga mätningen och beräkningen av jordens omkrets utfördes av Eratosthenes omkring 240 f.Kr. Uppskattningar av noggrannheten i Eratosthenes mätning sträcker sig från 0,5 % till 17 %. För både Aristoteles och Eratosthenes beror osäkerheten i noggrannheten av deras uppskattningar på modern osäkerhet över vilken stadionlängd de menade.

Omkring 100 f.Kr. räknade Posidonius av Apamea om jordens radie och fann att den var nära den av Eratosthenes, men senare tillskrev Strabo honom felaktigt ett värde på cirka 3/4 av den faktiska storleken. Claudius Ptolemaios omkring 150 AD gav empiriska bevis som stödde en sfärisk jord , men han accepterade det mindre värdet som tillskrivs Posidonius. Hans mycket inflytelserika verk, Almagest , lämnade inga tvivel bland medeltida forskare om att jorden är sfärisk, men de hade fel om dess storlek.

Vid 1490 trodde Christopher Colombus att resa 3 000 miles västerut från västkusten av den iberiska halvön skulle låta honom nå Asiens östra kuster . Emellertid förde 1492 antagandet av den resan hans flotta till Amerika . Magellanexpeditionen (1519–1522), som var den första världsomseglingen , demonstrerade väl jordens sfäricitet och bekräftade Eratosthenes ursprungliga mätning på 40 000 km (25 000 mi) .

Omkring 1690 hävdade Isaac Newton och Christiaan Huygens att jorden var närmare en oblate sfäroid än en sfär. Emellertid, runt 1730, argumenterade Jacques Cassini för en prolatsfäroid istället, på grund av olika tolkningar av den inblandade Newtonska mekaniken . För att lösa frågan mätte den franska geodesiska missionen (1735–1739) en latitud på två platser, en nära polcirkeln och den andra nära ekvatorn . Expeditionen fann att Newtons gissning var korrekt: jorden är tillplattad vid polerna på grund av rotationens centrifugalkraft .

Se även

• Jordens omkrets
• Jordmassa
• Effektiv jordradie
• Geodesi
• Geografiskt avstånd
• Oskulerande sfär
• Geodesins historia
• Mall:Jordens radie
• Planetarisk radie

externa länkar

• Merrifield, Michael R. (2010). " $R_{\oplus }$ Jordens radie (och exoplaneter)" . Sextio symboler . Brady Haran för University of Nottingham .