Astronomisk enhet
| Astronomisk enhet | |
|---|---|
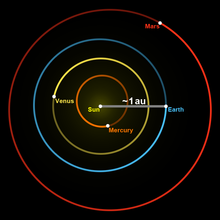 Den grå linjen indikerar avståndet jord–sol, vilket i genomsnitt är cirka 1 astronomisk enhet.
| |
| Allmän information | |
| Enhetssystem |
Astronomiskt system av enheter (godkänd för användning med SI) |
| Enhet av | längd |
| Symbol | au eller AU eller AU |
| Konverteringar | |
| 1 au eller AU eller AU i ... | ... är lika med ... |
| metriska ( SI ) enheter | 1 495 978 707 × 10 11 m |
| kejserliga och amerikanska enheter | 9,2956 × 10 7 mi |
| astronomiska enheter |
4,8481 × 10 −6 st 1,5813 × 10 −5 ly |
Den astronomiska enheten (symbol: au eller AU eller AU ) är en längdenhet , ungefär avståndet från jorden till solen och ungefär lika med 150 miljoner kilometer (93 miljoner miles) eller 8,3 ljusminuter. Det faktiska avståndet från jorden till solen varierar med cirka 3 % när jorden kretsar runt solen, från ett maximum ( aphelion ) till ett minimum ( perihelion ) och tillbaka igen en gång varje år. Den astronomiska enheten var ursprungligen tänkt som genomsnittet av jordens aphelion och perihelion; sedan 2012 har den dock definierats som exakt 149 597 870 700 m (se nedan för flera omvandlingar).
Den astronomiska enheten används främst för att mäta avstånd inom solsystemet eller runt andra stjärnor. Det är också en grundläggande komponent i definitionen av en annan enhet av astronomisk längd, parsec .
Historien om symbolanvändning
En mängd enhetssymboler och förkortningar har använts för den astronomiska enheten. I en resolution från 1976 International Astronomical Union (IAU) använt symbolen A för att beteckna en längd lika med den astronomiska enheten. I den astronomiska litteraturen var (och förblir) symbolen AU vanlig. 2006 International Bureau of Weights and Measures (BIPM) rekommenderat ua som symbol för enheten. I den icke-normativa bilagan C till ISO 80000-3 :2006 (nu indragen) var symbolen för den astronomiska enheten "ua".
År 2012 rekommenderade IAU, som noterade "att olika symboler för närvarande används för den astronomiska enheten", användningen av symbolen "au". De vetenskapliga tidskrifterna publicerade av American Astronomical Society och Royal Astronomical Society antog därefter denna symbol. I 2014 års revision och 2019 års upplaga av SI-broschyren använde BIPM enhetssymbolen "au". ISO 80000-3:2019, som ersätter ISO 80000-3:2006, nämner inte den astronomiska enheten.
Utveckling av enhetsdefinition
Jordens bana runt solen är en ellips . Halvhuvudaxeln i denna elliptiska omloppsbana definieras som hälften av det raka linjesegmentet som förenar perihelium och aphelium . Solens centrum ligger på detta raka linjesegment, men inte vid dess mittpunkt. Eftersom ellipser är välförstådda former, definierade mätning av punkterna för dess ytterligheter den exakta formen matematiskt och möjliggjorde beräkningar för hela omloppsbanan såväl som förutsägelser baserade på observation. Dessutom kartlade den exakt det största raka avståndet som jorden korsar under loppet av ett år, och definierade tider och platser för att observera den största parallaxen (skenbara positionsförskjutningar) i närliggande stjärnor. Att känna till jordens förskjutning och en stjärnas förskjutning gjorde det möjligt att beräkna stjärnans avstånd. Men alla mätningar är föremål för någon grad av fel eller osäkerhet, och osäkerheterna i längden på den astronomiska enheten ökade bara osäkerheterna i stjärnavstånden. Förbättringar av precision har alltid varit nyckeln till att förbättra astronomisk förståelse. Under hela 1900-talet blev mätningarna allt mer exakta och sofistikerade och allt mer beroende av noggrann observation av effekterna som beskrivs av Einsteins relativitetsteori och av de matematiska verktyg den använde.
Förbättrande mätningar kontrollerades kontinuerligt och korskontrollerades med hjälp av förbättrad förståelse av himmelmekanikens lagar , som styr objektens rörelser i rymden. De förväntade positionerna och avstånden för objekt vid en fastställd tidpunkt beräknas (i au) från dessa lagar och sätts samman till en samling data som kallas en efemeris . NASA :s Jet Propulsion Laboratory HORIZONS System tillhandahåller en av flera efemeriska beräkningstjänster.
1976, för att fastställa ett ännu exakt mått för den astronomiska enheten, antog IAU formellt en ny definition . Även om den var direkt baserad på de då bästa tillgängliga observationsmätningarna, omarbetades definitionen i termer av de då bästa matematiska härledningarna från himmelsmekanik och planetariska efemerider. Den angav att "den astronomiska längdenheten är den längd ( A ) för vilken den gaussiska gravitationskonstanten ( k ) har värdet 0,017 202 098 95 när måttenheterna är de astronomiska enheterna för längd, massa och tid". På motsvarande sätt, enligt denna definition, är en au "radien för en oberörd cirkulär Newtonsk bana kring solen för en partikel med oändlig massa, som rör sig med en vinkelfrekvens på 0,017 202 098 95 radianer per dag "; eller alternativt den längd för vilken den heliocentriska gravitationskonstanten (produkten GM ☉ ) är lika med ( 0,017 202 098 95 ) 2 au 3 /d 2 , när längden används för att beskriva objektens positioner i solsystemet.
Efterföljande undersökningar av solsystemet med rymdsonder gjorde det möjligt att erhålla exakta mätningar av de relativa positionerna för de inre planeterna och andra objekt med hjälp av radar och telemetri . Som med alla radarmätningar, är dessa beroende av att mäta tiden det tar för fotoner att reflekteras från ett objekt. Eftersom alla fotoner rör sig med ljusets hastighet i vakuum, en fundamental konstant för universum, beräknas ett objekts avstånd från sonden som produkten av ljusets hastighet och den uppmätta tiden. Men för precision kräver beräkningarna justering för saker som sondens och objektets rörelser medan fotonerna passerar. Dessutom måste själva mätningen av tiden översättas till en standardskala som tar hänsyn till relativistisk tidsutvidgning. Jämförelse av efemerispositionerna med tidsmätningar uttryckt i barycentrisk dynamisk tid (TDB) leder till ett värde för ljusets hastighet i astronomiska enheter per dag (på 86 400 s ). År 2009 hade IAU uppdaterat sina standardmått för att återspegla förbättringar och beräknat ljusets hastighet till 173.144 632 6847 (69) au/d (TDB).
00 1983 modifierade CIPM International System of Units (SI) för att göra mätaren definierad som avståndet tillryggalagt i vakuum av ljus på 1 / 299 792 458 sekund. Detta ersatte den tidigare definitionen, giltig mellan 1960 och 1983, som var att mätaren motsvarade ett visst antal våglängder av en viss emissionslinje av krypton-86. (Anledningen till förändringen var en förbättrad metod för att mäta ljusets hastighet.) Ljushastigheten kunde då uttryckas exakt som c = 299 792 458 m/s , en standard som också anammats av IERS numeriska standarder. Från denna definition och 2009 års IAU-standard visar sig tiden för ljus att passera en astronomisk enhet vara τ A = 499,004 783 8061 ± 0,000 000 01 s , vilket är något mer än 8 minuter och 19 sekunder. Genom multiplikation var den bästa uppskattningen av IAU 2009 A = c τ A = 149 597 870 700 ± 3 m , baserat på en jämförelse av Jet Propulsion Laboratory och IAA–RAS efemerider.
År 2006 rapporterade BIPM ett värde på den astronomiska enheten som 1,495 978 706 91 (6) × 10 11 m . I 2014 års revidering av SI-broschyren erkände BIPM IAU:s omdefiniering 2012 av den astronomiska enheten som 149 597 870 700 m .
Denna uppskattning härleddes fortfarande från observationer och mätningar som är föremål för fel, och baserade på tekniker som ännu inte standardiserade alla relativistiska effekter och därför inte var konstanta för alla observatörer. När IAU 2012 fann att enbart relativitetsutjämningen skulle göra definitionen alltför komplex, använde IAU helt enkelt 2009 års uppskattning för att omdefiniera den astronomiska enheten som en konventionell längdenhet direkt kopplad till metern (exakt 149 597 870 700 m ) . Den nya definitionen erkänner också som en konsekvens att den astronomiska enheten nu kommer att spela en roll av minskad betydelse, begränsad i dess användning till att vara en bekvämlighet i vissa tillämpningar.
1 astronomisk enhet = 149 597 870 700 meter (per definition) = 149 597 870.700 kilometer exakt 0.2 ljus år ≈ 4,848 ( ) −6 × ≈ 92 955 807.273 miles ≈ 499.004 783 84 ljussekunder ≈ 8.316 746 3973 ljusminuter 136 8111 5 ≈ 10 parsecs _ _
Denna definition gör ljusets hastighet, definierad som exakt 299 792 458 m/s , lika med exakt 299 792 458 × 86 400 ÷ 149 597 870 700 eller ungefär 173.144 632 674 240 60 delar per, trillion mindre 2009 års uppskattning.
Användning och betydelse
Med de definitioner som användes före 2012 var den astronomiska enheten beroende av den heliocentriska gravitationskonstanten , det vill säga produkten av gravitationskonstanten , G , och solmassan , M ☉ . Varken G eller M ☉ kan mätas med hög noggrannhet separat, men värdet av deras produkt är känt mycket exakt från observation av planeternas relativa positioner ( Keplers tredje lag uttryckt i termer av Newtonsk gravitation). Endast produkten krävs för att beräkna planetariska positioner för en efemeris, så efemerider beräknas i astronomiska enheter och inte i SI-enheter.
Beräkningen av efemerider kräver också ett övervägande av effekterna av allmän relativitet . Speciellt är tidsintervall uppmätta på jordens yta ( Terrestrial Time , TT) inte konstanta jämfört med planeternas rörelser: den jordiska sekunden (TT) verkar vara längre nära januari och kortare nära juli jämfört med "planetsekunden" " (konventionellt mätt i TDB). Detta beror på att avståndet mellan jorden och solen inte är fixerat (det varierar mellan 0,983 289 8912 och 1,016 710 3335 au ) och när jorden är närmare solen ( perihelion ) är solens gravitationsfält starkare och jorden rör sig snabbare längs dess omloppsbana. Eftersom mätaren är definierad i termer av sekunden och ljusets hastighet är konstant för alla observatörer, tycks den markbundna mätaren ändra i längd jämfört med "planetmetern" på en periodisk basis.
Mätaren definieras som en enhet med rätt längd , men SI-definitionen anger inte den metriska tensor som ska användas för att bestämma den. Internationella kommittén för vikter och mått (CIPM) noterar faktiskt att "dess definition gäller endast inom en rumslig omfattning som är tillräckligt liten för att effekterna av gravitationsfältets olikformighet kan ignoreras". Som sådan är mätaren odefinierad för att mäta avstånd inom solsystemet. 1976 års definition av den astronomiska enheten var ofullständig eftersom den inte specificerade referensramen inom vilken tiden ska mätas, men visade sig vara praktisk för beräkningen av efemerider: en mer fullständig definition som överensstämmer med allmän relativitet föreslogs, och "kraftig debatt" följde fram till augusti 2012 när IAU antog den nuvarande definitionen av 1 astronomisk enhet = 149 597 870 700 meter .
Den astronomiska enheten används vanligtvis för avstånd i stjärnsystemskala , såsom storleken på en protostellär skiva eller det heliocentriska avståndet för en asteroid, medan andra enheter används för andra avstånd inom astronomi . Den astronomiska enheten är för liten för att vara bekväm för interstellära avstånd, där parsec och ljusår används i stor utsträckning. Parsec (parallax arcsecond ) definieras i termer av den astronomiska enheten, som är avståndet för ett objekt med en parallax på 1″ . Ljusåret används ofta i populära verk, men är inte en godkänd icke-SI-enhet och används sällan av professionella astronomer.
När man simulerar en numerisk modell av solsystemet ger den astronomiska enheten en lämplig skala som minimerar ( bräddavlopp , underflöde och trunkering ) fel i flyttalsberäkningar .
Historia
Boken On the Sizes and Distances of the Sun and Moon , som tillskrivs Aristarchus , säger att avståndet till solen är 18 till 20 gånger avståndet till månen , medan det verkliga förhållandet är cirka 389,174 . Den senare uppskattningen baserades på vinkeln mellan halvmånen och solen, som han uppskattade till 87° (det sanna värdet är nära 89,853° ). Beroende på avståndet som van Helden antar att Aristarchus använde för avståndet till månen, skulle hans beräknade avstånd till solen falla mellan 380 och 1 520 jordradier.
Enligt Eusebius i Praeparatio evangelica (bok XV, kapitel 53) fann Eratosthenes att avståndet till solen var "σταδιων μυριαδας τετρακοσιας κασσως κατσς" bokstavligen "av stadier myriader 400 och 80 000 ″ ) men med den ytterligare noteringen att i den grekiska texten är den grammatiska överensstämmelsen mellan myriader (inte stadia ) å ena sidan och både 400 och 80 000 å andra sidan, som på grekiska, till skillnad från engelska, böjs alla tre (eller alla fyra om man skulle inkludera stadia ) ord Detta har översatts antingen till 4 080 000 stadier (översättning från 1903 av Edwin Hamilton Gifford ), eller till 804 000 000 stadia (upplagan av Édourad des Places [ de ] , daterad 1974–1991). Med hjälp av den grekiska stadion 19085 till 1908 meter, kommer den tidigare översättningen till 754 800 km till 775 200 km , vilket är alldeles för lågt, medan den andra översättningen kommer till 148,7 till 152,8 miljoner kilometer (exakt inom 2%). Hipparchus gav också en uppskattning av avståndet mellan Jorden från solen, citerad av Pappus som lika med 490 jordradier. Enligt de gissningsmässiga rekonstruktionerna av Noel Swerdlow och GJ Toomer härleddes detta från hans antagande om en "minst märkbar" solparallax på 7 ′ .
En kinesisk matematisk avhandling, Zhoubi Suanjing (ca 1:a århundradet f.Kr.), visar hur avståndet till solen kan beräknas geometriskt med hjälp av de olika längderna av middagsskuggorna som observeras på tre platser 1 000 li från varandra och antagandet att jorden är platt .
|
Avstånd till solen uppskattat med |
Uppskatta | I au | |
|---|---|---|---|
|
Solparallax _ |
Jordradier _ |
||
|
Aristarchus (3:e århundradet f.Kr.) (i On-storlekar ) |
13′ 24″ – 7′ 12″ | 256,5 – 477,8 | 0,011 – 0,020 |
|
Arkimedes (3:e århundradet f.Kr.) (i The Sand Reckoner ) |
21 tum | 10 000 | 0,426 |
| Hipparchus (2:a århundradet f.Kr.) | 7′ | 490 | 0,021 |
|
Posidonius (1:a århundradet f.Kr.) (citerad av den gamla Kleomedes ) |
21 tum | 10 000 | 0,426 |
| Ptolemaios (2:a århundradet) | 2′ 50″ | 1 210 | 0,052 |
| Godefroy Wendelin (1635) | 15 tum | 14 000 | 0,597 |
| Jeremiah Horrocks (1639) | 15 tum | 14 000 | 0,597 |
| Christiaan Huygens (1659) | 8,2 tum | 25 086 | 1,068 |
| Cassini & Richer (1672) | 9,5 tum | 21 700 | 0,925 |
| Flamsteed (1672) | 9,5 tum | 21 700 | 0,925 |
| Jérôme Lalande (1771) | 8,6 tum | 24 000 | 1,023 |
| Simon Newcomb (1895) | 8,80 tum | 23 440 | 0,9994 |
| Arthur Hinks (1909) | 8,807 tum | 23 420 | 0,9985 |
| H. Spencer Jones (1941) | 8 790 tum | 23 466 | 1,0005 |
| modern astronomi | 8 794 143 tum | 23 455 | 1 0000 |
På 200-talet e.Kr. uppskattade Ptolemaios medelavståndet för solen som 1 210 gånger jordens radie . För att bestämma detta värde började Ptolemaios med att mäta Månens parallax och hitta vad som motsvarade en horisontell månparallax på 1° 26′, vilket var alldeles för stort. härledde sedan ett maximalt månavstånd på 64 + 1/6 jordradier . På grund av upphävande fel i hans parallaxfigur, hans teori om månens bana och andra faktorer, var denna figur ungefär korrekt. Han mätte sedan de skenbara storlekarna på solen och månen och drog slutsatsen att solens skenbara diameter var lika med månens skenbara diameter på månens största avstånd, och från register över månförmörkelser uppskattade han denna skenbara diameter, som samt den skenbara diametern på jordens skuggkon som månen genomkorsar under en månförmörkelse. Givet dessa data kan solens avstånd från jorden trigonometriskt beräknas till 1 210 jordradier. Detta ger ett förhållande mellan sol- och månavstånd på cirka 19, vilket matchar Aristarchus figur. Även om Ptolemaios procedur är teoretiskt genomförbar, är den väldigt känslig för små förändringar i data, så mycket att en förändring av en mätning med några procent kan göra solavståndet oändligt.
Efter att grekisk astronomi överfördes till den medeltida islamiska världen, gjorde astronomer vissa förändringar i Ptolemaios kosmologiska modell, men ändrade inte i någon större utsträckning hans uppskattning av avståndet jord–sol. Till exempel, i sin introduktion till ptolemaisk astronomi, al-Farghānī ett medelsolavstånd på 1 170 jordradier, medan al-Battānī i sin zij använde ett medelsolavstånd på 1 108 jordradier. Efterföljande astronomer, som al-Bīrūnī , använde liknande värden. Senare i Europa Copernicus och Tycho Brahe också jämförbara siffror ( 1 142 och 1 150 jordradier), och så överlevde Ptolemaios ungefärliga avstånd mellan jord och sol genom 1500-talet.
Johannes Kepler var den första som insåg att Ptolemaios uppskattning måste vara betydligt för låg (enligt Kepler, åtminstone med en faktor tre) i hans Rudolphine Tables (1627). Keplers lagar för planetrörelser gjorde det möjligt för astronomer att beräkna planeternas relativa avstånd från solen, och återuppväckte intresset för att mäta det absoluta värdet för jorden (som sedan kunde tillämpas på de andra planeterna). Uppfinningen av teleskopet möjliggjorde mycket mer exakta mätningar av vinklar än vad som är möjligt med blotta ögat. Den flamländska astronomen Godefroy Wendelin upprepade Aristarchus mätningar 1635 och fann att Ptolemaios värde var för lågt med en faktor på minst elva.
En något mer exakt uppskattning kan erhållas genom att observera Venus transit . Genom att mäta transiteringen på två olika platser kan man exakt beräkna Venus parallax och från det relativa avståndet mellan Jorden och Venus från solen, solparallaxen α ( som inte kan mätas direkt på grund av solens ljusstyrka). Jeremiah Horrocks hade försökt göra en uppskattning baserad på hans observation av transiteringen 1639 (publicerad 1662), vilket gav en solparallax på 15 ″ , liknande Wendelins figur. Solparallaxen är relaterad till avståndet jord–sol mätt i jordens radier med
Ju mindre solparallaxen är, desto större är avståndet mellan solen och jorden: en solparallax på 15″ motsvarar ett avstånd jord–sol på 13 750 jordradier.
Christiaan Huygens trodde att avståndet var ännu större: genom att jämföra de skenbara storlekarna på Venus och Mars uppskattade han ett värde på cirka 24 000 jordradier, vilket motsvarar en solparallax på 8,6″ . Även om Huygens uppskattning är anmärkningsvärt nära moderna värderingar, diskonteras den ofta av astronomihistoriker på grund av de många obevisade (och felaktiga) antaganden han var tvungen att göra för att hans metod skulle fungera; noggrannheten av hans värde verkar mer baseras på tur än bra mätning, med hans olika fel som tar bort varandra.

Jean Richer och Giovanni Domenico Cassini mätte Mars parallax mellan Paris och Cayenne i Franska Guyana när Mars var som närmast jorden 1672. De kom fram till en siffra för solparallaxen på 9,5 tum , motsvarande ett avstånd mellan jord och sol på cirka 22 000 jordradier. De var också de första astronomerna som hade tillgång till ett exakt och tillförlitligt värde för jordens radie, som hade uppmätts av deras kollega Jean Picard 1669 som 3 269 000 toises . Samma år sågs en annan uppskattning för den astronomiska enheten av John Flamsteed , som åstadkom den ensam genom att mäta Mars dagparallax . En annan kollega, Ole Rømer , upptäckte ljusets ändliga hastighet 1676: hastigheten var så stor att den vanligtvis angavs som den tid som krävs för ljuset att resa från solen till jorden, eller "ljustid per enhet avstånd", en konvention som fortfarande följs av astronomer idag.
En bättre metod för att observera Venus transiter utarbetades av James Gregory och publicerades i hans Optica Promata (1663). Det förespråkades starkt av Edmond Halley och tillämpades på Venuspassager som observerades 1761 och 1769, och sedan igen 1874 och 1882. Venuspassager förekommer i par, men mindre än ett par varje århundrade, och observerade transiteringar 1761 och 1769 var en aldrig tidigare skådad internationell vetenskaplig operation inklusive observationer av James Cook och Charles Green från Tahiti. Trots sjuårskriget skickades dussintals astronomer till observationsplatser runt om i världen till stor kostnad och personlig fara: flera av dem dog i strävan. De olika resultaten sammanställdes av Jérôme Lalande för att ge en siffra för solparallaxen på 8,6″ . Karl Rudolph Powalky hade gjort en uppskattning på 8,83 tum 1864.
| Datum | Metod | A /Gm | Osäkerhet |
|---|---|---|---|
| 1895 | avvikelse | 149,25 | 0,12 |
| 1941 | parallax | 149,674 | 0,016 |
| 1964 | radar | 149,5981 | 0,001 |
| 1976 | telemetri | 149.597 870 | 0,000 001 |
| 2009 | telemetri | 149,597 870 700 | 0,000 000 003 |
En annan metod var att bestämma aberrationskonstanten . Simon Newcomb lade stor vikt åt denna metod när han härledde sitt allmänt accepterade värde på 8,80″ för solparallaxen (nära det moderna värdet på 8,794 143 ″ ), även om Newcomb också använde data från Venus transiter. Newcomb samarbetade också med A. A. Michelson för att mäta ljusets hastighet med jordbaserad utrustning; kombinerat med aberrationskonstanten (som är relaterad till ljustiden per avståndsenhet) gav detta den första direkta mätningen av avståndet jord–sol i kilometer. Newcombs värde för solparallaxen (och för aberrationskonstanten och den gaussiska gravitationskonstanten) införlivades i det första internationella systemet av astronomiska konstanter 1896, som fanns kvar för beräkningen av efemerider fram till 1964. Namnet "astronomisk enhet" verkar först ha använts 1903. [ misslyckad verifiering ]
Upptäckten av den jordnära asteroiden 433 Eros och dess passage nära jorden 1900–1901 möjliggjorde en avsevärd förbättring av parallaxmätningen. Ett annat internationellt projekt för att mäta parallaxen av 433 Eros genomfördes 1930–1931.
Direkta radarmätningar av avstånden till Venus och Mars blev tillgängliga i början av 1960-talet. Tillsammans med förbättrade mätningar av ljusets hastighet visade dessa att Newcombs värden för solparallaxen och aberrationskonstanten var inkonsekventa med varandra.
Utvecklingen

Enhetsavståndet A (värdet av den astronomiska enheten i meter) kan uttryckas i termer av andra astronomiska konstanter:
där G är den Newtonska gravitationskonstanten , M ☉ är solmassan, k är det numeriska värdet för Gauss gravitationskonstant och D är tidsperioden för en dag. Solen tappar ständigt i massa genom att stråla bort energi, så planeternas banor expanderar stadigt utåt från solen. Detta har lett till uppmaningar att överge den astronomiska enheten som måttenhet.
Eftersom ljusets hastighet har ett exakt definierat värde i SI-enheter och den gaussiska gravitationskonstanten k är fixerad i det astronomiska enhetssystemet, är mätning av ljustiden per enhetssträcka exakt ekvivalent med att mäta produkten G × M ☉ i SI-enheter. Därför är det möjligt att konstruera efemerider helt i SI-enheter, vilket alltmer blir normen.
En analys från 2004 av radiometriska mätningar i det inre solsystemet antydde att den sekulära ökningen av enhetsavståndet var mycket större än vad som kan förklaras av solstrålning, + 15 ± 4 meter per århundrade.
Mätningarna av de sekulära variationerna av den astronomiska enheten bekräftas inte av andra författare och är ganska kontroversiella. Sedan 2010 har den astronomiska enheten dessutom inte uppskattats av de planetariska efemeriderna.
Exempel
Följande tabell innehåller några avstånd som anges i astronomiska enheter. Den innehåller några exempel med avstånd som normalt inte anges i astronomiska enheter, eftersom de antingen är för korta eller alldeles för långa. Avstånden förändras normalt över tiden. Exempel listas efter ökande avstånd.
| Objekt | Längd eller avstånd (au) | Räckvidd | Kommentar och referenspunkt | Refs |
|---|---|---|---|---|
| Ljus-sekund | 0,0019 | – | sträcka ljuset färdas på en sekund | – |
| Månens avstånd | 0,0026 | – | genomsnittligt avstånd från jorden (som Apollo-uppdragen tog cirka 3 dagar att resa) | – |
| Solradie | 0,005 | – | solens radie ( 695 500 km , 432 450 mi , hundra gånger jordens radie eller tio gånger medelradien för Jupiter) | – |
| Ljusminut | 0,12 | – | sträcka ljuset färdas på en minut | – |
| Merkurius | 0,39 | – | medelavstånd från solen | – |
| Venus | 0,72 | – | medelavstånd från solen | – |
| Jorden | 1.00 | – | genomsnittligt avstånd från jordens omloppsbana från solen ( solljuset färdas i 8 minuter och 19 sekunder innan det når jorden) | – |
| Mars | 1,52 | – | medelavstånd från solen | – |
| Jupiter | 5.2 | – | medelavstånd från solen | – |
| Ljustimmar | 7.2 | – | sträcka ljuset färdas på en timme | – |
| Saturnus | 9.5 | – | medelavstånd från solen | – |
| Uranus | 19.2 | – | medelavstånd från solen | – |
| Kuiperbälte | 30 | – | Innerkanten börjar vid cirka 30 au | |
| Neptunus | 30.1 | – | medelavstånd från solen | – |
| Eris | 67,8 | – | medelavstånd från solen | – |
| Voyager 2 | 132 | – | avstånd från solen i februari 2023 | |
| Voyager 1 | 159 | – | avstånd från solen i februari 2023 | |
| Ljus-dag | 173 | – | sträcka ljuset färdas på en dag | – |
| Ljusår | 63 241 | – | avstånd ljus färdas under ett julianskt år (365,25 dagar) | – |
| Oort moln | 75 000 | ± 25 000 | avståndet från den yttre gränsen för Oorts moln från solen (uppskattat motsvarar 1,2 ljusår) | – |
| Parsec | 206 265 | – | en parsec . Parsec definieras i termer av den astronomiska enheten, används för att mäta avstånd utanför solsystemets räckvidd och är cirka 3,26 ljusår: 1 st = 1 au/tan(1″) | |
| Proxima Centauri | 268 000 | ± 126 | avstånd till närmaste stjärna till solsystemet | – |
| Galactic Center | 1 700 000 000 | – | avstånd från solen till mitten av Vintergatan | – |
| Notera: siffrorna i denna tabell är i allmänhet avrundade, uppskattningar, ofta grova uppskattningar, och kan avsevärt skilja sig från andra källor. Tabellen innehåller även andra längdenheter för jämförelse. | ||||
Se även
Vidare läsning
- Williams, D.; Davies, RD (1968). "En radiometod för att bestämma den astronomiska enheten" . Månatliga meddelanden från Royal Astronomical Society . 140 (4): 537. Bibcode : 1968MNRAS.140..537W . doi : 10.1093/mnras/140.4.537 .
externa länkar
- IAU och astronomiska enheter
- Rekommendationer angående enheter (HTML-version av IAU Style Manual)
- Jagar Venus, observerar Venus genomgångar
- Transit av Venus