Hasse diagram

Ej att förväxla med Hess-diagrammet .

Effektuppsättningen av en 2 - elementsuppsättning ordnad efter inkludering

I ordningsteori är ett Hasse-diagram ( / ˈ h æ s ə / ; tyska: [ˈhasə] ) en typ av matematiskt diagram som används för att representera en finit partiellt ordnad uppsättning , i form av en ritning av dess transitiva reduktion . Konkret, för en delvis ordnad uppsättning $(S,\leq )$ representerar man varje element i $S$ som en vertex i planet och ritar ett linjesegment eller kurva som går uppåt från en vertex $x$ till en annan vertex $y$ när $y$ täcker $x$ (det vill säga när $x\neq y$ , $x\leq y$ och det finns ingen $z$ skild från $x$ och $y$ med $x\leq z\leq y$ ). Dessa kurvor kan korsa varandra men får inte vidröra några andra hörn än deras ändpunkter. Ett sådant diagram, med märkta hörn, bestämmer unikt dess partiella ordning.

Hasse diagram är uppkallade efter Helmut Hasse (1898–1979); enligt Garrett Birkhoff kallas de så på grund av den effektiva användningen Hasse gjort av dem. Hasse var dock inte den första som använde dessa diagram. Ett exempel som går före Hasse finns i Henri Gustave Vogt ( 1895 ). Även om Hasse-diagram ursprungligen skapades som en teknik för att göra ritningar av delvis ordnade uppsättningar för hand, har de på senare tid skapats automatiskt med hjälp av grafritningstekniker .

Frasen "Hasse-diagram" kan också hänvisa till den transitiva reduktionen som en abstrakt riktad acyklisk graf , oberoende av någon ritning av den grafen, men denna användning undviks här.

Diagram design

Även om Hasse-diagram är enkla och intuitiva verktyg för att hantera ändliga poser , visar det sig vara ganska svårt att rita "bra" diagram. Anledningen är att det i allmänhet kommer att finnas många möjliga sätt att rita ett Hasse-diagram för en given poset. Den enkla tekniken att bara börja med de minimala elementen i en beställning och sedan rita större element inkrementellt ger ofta ganska dåliga resultat: symmetrier och inre struktur i beställningen går lätt förlorade.

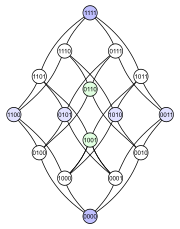
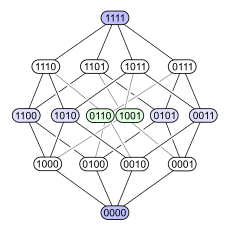
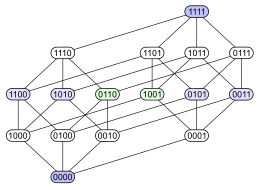
Följande exempel visar problemet. Betrakta effektmängden för en 4-elementsmängd ordnad efter inkludering $\subseteq$ . Nedan finns fyra olika Hasse-diagram för denna delordning. Varje delmängd har en nod märkt med en binär kodning som visar om ett visst element finns i delmängden (1) eller inte (0):

Det första diagrammet klargör att kraftuppsättningen är en graderad poset . Det andra diagrammet har samma graderade struktur, men genom att göra vissa kanter längre än andra, betonar det att den 4-dimensionella kuben är en kombinatorisk förening av två 3-dimensionella kuber, och att en tetraeder ( abstrakt 3-polytop) likaledes slår samman två trianglar ( abstrakta 2-polytoper ). Det tredje diagrammet visar en del av strukturens inre symmetri. I det fjärde diagrammet är hörnen ordnade som elementen i en 4×4- matris .

Planaritet uppåt

Huvudartikel: Uppåtgående plan ritning

Detta Hasse-diagram av gittret av undergrupper av den dihedriska gruppen Dih ₄ har inga korsande kanter.

Om en partiell ordning kan ritas som ett Hasse-diagram där inga två kanter korsar, sägs dess täckande graf vara uppåtgående plan . Ett antal resultat om planaritet uppåt och om korsningsfri Hasse-diagramkonstruktion är kända:

• Om den delordning som ska ritas är ett gitter , kan den ritas utan korsningar om och endast om den har en ordningsdimension som högst två. I det här fallet kan en icke-korsande ritning hittas genom att härleda kartesiska koordinater för elementen från deras positioner i de två linjära ordningarna som realiserar ordningsdimensionen, och sedan rotera ritningen moturs med en 45-graders vinkel.
• Om den partiella ordningen har högst ett minimalt element , eller den har högst ett maximalt element , kan det testas i linjär tid om den har ett icke-korsande Hasse-diagram.
• Det är NP-komplett för att avgöra om en delordning med flera källor och sänkor kan ritas som ett korsningsfritt Hasse-diagram. Att hitta ett korsningsfritt Hasse-diagram är dock handhavbart med fasta parametrar när det parametriseras av antalet artikulationspunkter och trekopplade komponenter i den transitiva reduktionen av delordningen.
• Om y -koordinaterna för elementen i en delordning är specificerade, kan ett korsningsfritt Hasse-diagram som respekterar dessa koordinattilldelningar hittas i linjär tid, om ett sådant diagram finns. I synnerhet, om ingångsposet är en graderad poset , är det möjligt att bestämma i linjär tid om det finns ett korsningsfritt Hasse-diagram där höjden på varje vertex är proportionell mot dess rang.

UML-notation

Ett klassdiagram som visar multipelt arv

Inom mjukvaruteknik avbildas klasserna i ett mjukvarusystem och arvsrelationen mellan dessa klasser ofta med hjälp av ett klassdiagram , en form av Hasse-diagram där kanterna som förbinder klasserna ritas som heldragna linjesegment med en öppen triangel i superklassänden .

Anteckningar

• Baker, Kirby A.; Fishburn, Peter C .; Roberts, Fred S. (1971), "Partial orders of dimension 2", Networks , 2 (1): 11–28, doi : 10.1002/net.3230020103
•   Bang-Jensen, Jørgen (2008), "2.1 Acyclic Digraphs", Digraphs: Theory, Algorithms and Applications , Springer Monographs in Mathematics (2nd ed.), Springer-Verlag, s. 32–34, ISBN 978-1-84800- 997-4
•   Bertolazzi, R; Di Battista, G.; Mannino, C.; Tamassia, R. (1993), "Optimal upward planarity testing of single-source digraphs" (PDF) , Proc. 1st European Symposium on Algorithms (ESA '93) , Lecture Notes in Computer Science, vol. 726, Springer-Verlag, s. 37–48, doi : 10.1007/3-540-57273-2_42 , ISBN 978-3-540-57273-2
• Birkhoff, Garrett (1948), Lattice Theory (reviderad utg.), American Mathematical Society
• Chan, Hubert (2004), "En parametriserad algoritm för uppåtgående planaritetstestning", Proc. 12th European Symposium on Algorithms (ESA '04) , Lecture Notes in Computer Science, vol. 3221, Springer-Verlag, s. 157–168, doi : 10.1007/978-3-540-30140-0_16
• Christofides, Nicos (1975), Graph theory: an algorithmic approach , Academic Press, s. 170–174
• Di Battista, G.; Tamassia, R. (1988), "Algorithms for plane representation of acyclic digraphs", Theoretical Computer Science , 61 (2–3): 175–178, doi : 10.1016/0304-3975(88)90123-5
• Freese, Ralph (2004), "Automated lattice drawing", Concept Lattices (PDF) , Lecture Notes in Computer Science, vol. 2961, Springer-Verlag, s. 589–590
•   Garg, Ashim; Tamassia, Roberto (1995a), "Upward planarity testing", Order , 12 (2): 109–133, doi : 10.1007/BF01108622 , S2CID 14183717
•   Garg, Ashim; Tamassia, Roberto (1995b), "On the computational complexity of upward and rectilinear planarity testing", Graph Drawing (Proc. GD '94) , LectureNotes in Computer Science, vol. 894, Springer-Verlag, s. 286–297, doi : 10.1007/3-540-58950-3_384 , ISBN 978-3-540-58950-1
•   Jünger, Michael; Leipert, Sebastian (1999), "Level planar embedding in linear time", Graph Drawing (Proc. GD '99) , Lecture Notes in Computer Science, vol. 1731, s. 72–81, doi : 10.1007/3-540-46648-7_7 , ISBN 978-3-540-66904-3
•   Rival, Ivan (1985), "The diagram", i Rival, Ivan (red.), Graphs and Order: The Role of Graphs in the Theory of Ordered Sets and Its Applications, Proceedings of the NATO Advanced Study Institute som hölls i Banff, 18–31 maj 1984 , NATO Advanced Science Institutes Series C: Mathematical and Physical Sciences, vol. 147, Reidel, Dordrecht, s. 103–133, MR 0818494
•   Thulasiraman, K.; Swamy, MNS (1992), "5.7 Acyclic Directed Graphs", Graphs: Theory and Algorithms , John Wiley och Son, sid. 118, ISBN 978-0-471-51356-8
• Vogt, Henri Gustave (1895), Leçons sur la résolution algébrique des équations , Nony, sid. 91

externa länkar

• Relaterade medier på Wikimedia Commons:
  • Hasse diagram (Galleri)
  • Hasse-diagram (Kategori)
• Weisstein, Eric W. , "Hasse Diagram" , MathWorld