Homogent förhållande

Inom matematiken är en homogen relation (även kallad endorelation ) över en mängd X en binär relation över X och sig själv, dvs det är en delmängd av den kartesiska produkten $X \times X$ . Detta uttrycks vanligtvis som "en relation på X " eller "en (binär) relation över X ". Ett exempel på en homogen relation är relationen släktskap , där relationen är över människor.

Vanliga typer av anteckningar inkluderar ordningar , grafer och ekvivalenser . Specialiserade studier orderteori och grafteori har utvecklat förståelse för endorelationer. Terminologi som är specifik för grafteori används för beskrivning, med en vanlig graf antas motsvara en symmetrisk relation , och en allmän endorelation som motsvarar en riktad graf . En endorelation R motsvarar en logisk matris av 0s och 1s, där uttrycket xRy motsvarar en kant mellan x och y i grafen, och till en 1 i kvadratmatrisen för R . Det kallas en närliggande matris i grafterminologi.

Särskilt homogena relationer

Några speciella homogena relationer över en mängd X (med godtyckliga element $x 1$ , $x 2$ ) är:

Tom relation

$E = \emptyset$ ; det vill säga $x 1 Ex 2$ gäller aldrig;
Universell relation

$U = X \times X$ ; det vill säga $x 1 Ux 2$ gäller alltid;
Identitetsrelation (se även identitetsfunktion )

$I = {(x, x) | x \in X$ }; det vill säga $x 1 Ix 2$ gäller om och endast om $x 1 = x 2$ .

Exempel

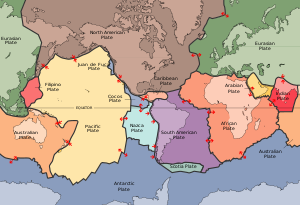
Femton stora tektoniska plattor av jordskorpan kontaktar varandra i ett homogent förhållande. Relationen kan uttryckas som en logisk matris där 1 anger kontakt och 0 ingen kontakt. Detta exempel uttrycker en symmetrisk relation.

Egenskaper

Några viktiga egenskaper som en homogen relation $R$ över en mängd $X$ kan ha är:

Reflexiv: för alla $x \in X$ , $xRx$ . Till exempel är ≥ en reflexiv relation men > är det inte.
Irreflexiv (eller strikt ): för alla $x \in X$ , inte $xRx$ . Till exempel är > en irreflexiv relation, men ≥ är det inte.
Coreflexiv: för alla $x, y \in X$ , om $xRy$ så är $x = y$ . Till exempel är relationen över heltal där varje udda tal är relaterat till sig självt en kärnflexiv relation. Jämlikhetsrelationen är det enda exemplet på en både reflexiv och coreflexiv relation, och varje coreflexiv relation är en delmängd av identitetsrelationen.
Vänster kvasireflexiv: för alla $x, y \in X$ , om $xRy$ så $xRx$ .
Höger kvasireflexiv: för alla $x, y \in X$ , om $xRy$ så $yRy$ .
Kvasireflexiv: för alla $x, y \in X$ , om $xRy$ så $xRx$ och $yRy$ . En relation är kvasi-reflexiv om, och endast om, den är både vänster och höger kvasi-reflexiv.

De föregående 6 alternativen är långt ifrån uttömmande; t.ex. är den röda binära relationen $y = x 2$ varken irreflexiv, inte coreflexiv eller reflexiv, eftersom den innehåller paret $(0, 0)$ respektive $(2, 4)$ , men inte $(2, 2)$ . De två sistnämnda fakta utesluter också (alla slags) kvasi-reflexivitet.

Symmetrisk: för alla $x, y \in X$ , om $xRy$ så $yRx$ . Till exempel är "är en blodsläkting till" en symmetrisk relation, eftersom $x$ är en blodsläkting till $y$ om och endast om $y$ är en blodsläkting till $x$ .
Antisymmetrisk: för alla $x, y \in X$ , om $xRy$ och $yRx$ så är $x = y$ . Till exempel är ≥ en antisymmetrisk relation; så är >, men vacuously (villkoret i definitionen är alltid falskt).
Asymmetrisk: för alla $x, y \in X$ , om $xRy$ så inte $yRx$ . En relation är asymmetrisk om och bara om den är både antisymmetrisk och irreflexiv. Till exempel är > en asymmetrisk relation, men ≥ är det inte.

Återigen, de tre föregående alternativen är långt ifrån uttömmande; som ett exempel över de naturliga talen är relationen $xRy$ definierad av $x > 2$ varken symmetrisk eller antisymmetrisk, än mindre asymmetrisk.

Transitiv: för alla $x, y, z \in X$ , om $xRy$ och $yRz$ så $xRz$ . En transitiv relation är irreflexiv om och endast om den är asymmetrisk. Till exempel är "är förfader till" en transitiv relation, medan "är förälder till" inte är det.
Antitransitiv: för alla $x, y, z \in X$ , om $xRy$ och $yRz$ så aldrig $xRz$ .
Kotransitiv: om komplementet till R är transitivt. Det vill säga för alla $x, y, z \in X$ , om $xRz$ , då $xRy$ eller $yRz$ . Detta används i pseudo-ordningar i konstruktiv matematik.
Kvasitransitiv: för alla $x, y, z \in X$ , om $xRy$ och $yRz$ men varken $yRx$ eller $zRy$ , då $xRz$ men inte $zRx$ .
Transitivitet för injämförbarhet: för alla $x, y, z \in X$ , om $x$ och $y$ är oförjämförliga med avseende på $R$ och om detsamma gäller för $y$ och $z$ , så är $x$ och $z$ också oförjämförliga med avseende på $R$ . Detta används i svaga beställningar .

Återigen, de tidigare 5 alternativen är inte uttömmande. Till exempel, relationen $xRy$ if ( $y = 0$ eller $y = x +1$ ) uppfyller ingen av dessa egenskaper. Å andra sidan tillfredsställer den tomma relationen trivialt dem alla.

Tät: för alla $x, y \in X$ så att $xRy$ , det finns några $z \in X$ så att $xRz$ och $zRy$ . Detta används i täta ordningsföljder .
Ansluten: för alla $x, y \in X$ , om $x \neq y$ så $xRy$ eller $yRx$ . Den här egenskapen kallas ibland ^{för "totalt", vilket skiljer sig från definitionerna av "vänster / höger-totalt "} nedan.
Starkt ansluten: för alla $x, y \in X$ , $xRy$ eller $yRx$ . Även denna egenskap kallas ibland ^{[ citat behövs ]} "totalt", vilket skiljer sig från definitionerna av "vänster/höger-totalt" nedan.
Trikotom: för alla $x, y \in X$ , exakt en av $xRy$ , $yRx$ eller $x = y$ gäller. Till exempel är > en trikotom relation, medan relationen "delar" över de naturliga talen inte är det.
Höger euklidiskt (eller bara euklidiskt ): för alla $x, y, z \in X$ , om $xRy$ och $xRz$ så $yRz$ . Till exempel är = en euklidisk relation eftersom om $x = y$ och $x = z$ så är $y = z$ .
Vänster euklidiskt: för alla $x, y, z \in X$ , om $yRx$ och $zRx$ så $yRz$ .
Välgrundad innehåller: varje icke-tom delmängd $S$ av $X$ ett minimalt element med avseende på $R$ . Välgrundadhet innebär det fallande kedjans tillstånd (det vill säga ingen oändlig kedja ... $x n R ... Rx 3 Rx 2 Rx 1$ kan existera). Om axiomet för beroende val antas är båda villkoren likvärdiga.

Dessutom kan alla egenskaper hos binära relationer i allmänhet också gälla för homogena relationer:

Mängdliknande: för alla $x \in X$ , klassen för alla $y$ så att $yRx$ är en mängd . (Detta är bara meningsfullt om relationer över korrekta klasser är tillåtna.)
Vänsterunikt: för alla $x, z \in X$ och alla $y \in Y$ , om $xRy$ och $zRy$ så är $x = z$ .
Univalent: för alla $x \in X$ och alla $y, z \in Y$ , om $xRy$ och $xRz$ så är $y = z$ .
Totalt (även kallat vänster-total): för alla $x \in X$ finns det ett $y \in Y$ så att $xRy$ . Den här egenskapen skiljer sig från definitionen av ansluten (även kallad total av vissa författare). ^{[ citat behövs ]}
Surjektiv (även kallad höger-total): för alla $y \in Y$ , det finns ett $x \in X$ så att xRy .

En förbeställning är en relation som är reflexiv och transitiv. En total förordning , även kallad linjär förordning eller svag ordning , är en relation som är reflexiv, transitiv och sammankopplad.

En partiell ordning , även kallad ordning , ^{[ citat behövs ]} är en relation som är reflexiv, antisymmetrisk och transitiv. En strikt partiell ordning , även kallad strikt ordning , ^{[ citat behövs ]} är en relation som är irreflexiv, antisymmetrisk och transitiv. En total ordning , även kallad linjär ordning , enkel ordning , eller kedja , är en relation som är reflexiv, antisymmetrisk, transitiv och sammankopplad. En strikt totalordning , även kallad strikt linjär ordning , strikt enkel ordning , eller strikt kedja , är en relation som är irreflexiv, antisymmetrisk, transitiv och sammankopplad.

En partiell ekvivalensrelation är en relation som är symmetrisk och transitiv. En ekvivalensrelation är en relation som är reflexiv, symmetrisk och transitiv. Det är också en relation som är symmetrisk, transitiv och total, eftersom dessa egenskaper innebär reflexivitet.

Implikationer och konflikter mellan egenskaper hos homogena binära relationer
Implikationer (blå) och konflikter (röd) mellan egenskaper (gul) hos homogena binära relationer. Till exempel är varje asymmetrisk relation irreflexiv ( " ASym ⇒ Irrefl " ), och ingen relation på en icke-tom mängd kan vara både irreflexiv och reflexiv ( " Irrefl # Refl " ). Att utelämna de röda kanterna resulterar i ett Hasse-diagram .

Operationer

Om R är ett homogent förhållande över en mängd X är vart och ett av följande ett homogent förhållande över X :

Reflexiv stängning , R ⁼: Definieras som $R = = {(x, x) | x \in X} \cup R$ eller den minsta reflexiva relationen över X som innehåller R . Detta kan bevisas vara lika med skärningspunkten mellan alla reflexiva relationer som innehåller R .
Reflexiv reduktion , R ^≠: Definierat som $R ≠ = R \ {( x , x ) | x ∈ X }$ eller den största irreflexiva relationen över X som finns i R .
Transitiv stängning , R ⁺: Definieras som den minsta transitiva relationen över X som innehåller R. Detta kan ses vara lika med skärningspunkten för alla transitiva relationer som innehåller R .
Reflexiv transitiv stängning , R *: Definieras som $R * = (R +) =$ , den minsta förbeställningen innehåller R . Reflexiv transitiv; Definieras som den minsta ekvivalensrelationen över X som innehåller R. symmetrisk
stängning , R ^≡

Alla operationer definierade i Binär relation § Operationer på binära relationer gäller även för homogena relationer.

Homogena förhållanden efter egendom
	Reflexivitet	Symmetri	Transitivitet	Samhörighet	Symbol	Exempel
Riktad graf					→
Oriktad graf		Symmetrisk
Beroende	Reflexiv	Symmetrisk
Turnering	Irreflexiv	Asymmetrisk				Hackordning
Förboka	Reflexiv		Transitiv		≤	Preferens
Total förbeställning	Reflexiv		Transitiv	Ansluten	≤
Delordning	Reflexiv	Antisymmetrisk	Transitiv		≤	Delmängd
Strikt delordning	Irreflexiv	Asymmetrisk	Transitiv		<	Strikt delmängd
Total beställning	Reflexiv	Antisymmetrisk	Transitiv	Ansluten	≤	Alfabetisk ordning
Strikt total beställning	Irreflexiv	Asymmetrisk	Transitiv	Ansluten	<	Strikt alfabetisk ordning
Partiell ekvivalensrelation		Symmetrisk	Transitiv
Ekvivalensförhållande	Reflexiv	Symmetrisk	Transitiv		∼, ≡	Jämlikhet

Uppräkning

Mängden av alla homogena relationer ${\mathcal {B}}(X)$ över en mängd X är mängden $2 X \times X$ som är en boolesk algebra utökad med involutionen av mappning av en relation till dess omvända relation . Om man betraktar sammansättning av relationer som en binär operation på ${\displaystyle {\mathcal {B}}(X)} ,$ bildar den en monoid med involution där identitetselementet är identitetsrelationen.

Antalet distinkta homogena relationer över en n -elementmängd är $2 n 2$ (sekvens A002416 i OEIS ):

Antal n -element binära relationer av olika typer
Element	Några	Transitiv	Reflexiv	Symmetrisk	Förboka	Delordning	Total förbeställning	Total beställning	Ekvivalensförhållande
0	1	1	1	1	1	1	1	1	1
1	2	2	1	2	1	1	1	1	1
2	16	13	4	8	4	3	3	2	2
3	512	171	64	64	29	19	13	6	5
4	65,536	3 994	4 096	1 024	355	219	75	24	15
n	2 ^{n ²}		2 ^{n ² − n}	2 ^{n ( n +1)/2}			${\textstil \sum _{k=0}^{n}k!S(n,k)}$	n !	${\textstil \sum _{k=0}^{n}S(n,k)}$
OEIS	A002416	A006905	A053763	A006125	A000798	A001035	A000670	A000142	A000110

Observera att $S (n, k)$ hänvisar till Stirlingtal av det andra slaget .

Anmärkningar:

Antalet irreflexiva relationer är detsamma som antalet reflexiva relationer.
Antalet strikta partiella order (irreflexiva transitiva relationer) är detsamma som för partiella order.
Antalet strikt svaga beställningar är detsamma som för totala förbeställningar.
De totala beställningarna är de delordrar som också är totala förbeställningar. Antalet förbeställningar som varken är en delorder eller en total förbeställning är därför antalet förbeställningar, minus antalet delbeställningar, minus antalet totala förbeställningar, plus antalet totala beställningar: 0, 0, 0, 3 respektive 85.
Antalet ekvivalensrelationer är antalet partitioner , vilket är Bell-numret .

De homogena relationerna kan grupperas i par (relation, komplement ), förutom att för $n = 0$ är relationen ett eget komplement. De icke-symmetriska kan grupperas i fyrdubblar (relation, komplement, invers , invers komplement).

Exempel

Orderrelationer , inklusive strikta order :
- Större än
- Större än eller lika med
- Mindre än
- Mindre än eller lika med
- Delar (jämnt)
- Delmängd av
Ekvivalensrelationer :
- Jämlikhet
- Parallellt med (för affina mellanslag )
- Equinumerosity eller "är i bijection med"
- Isomorf
- Equipollent linjesegment
Toleransrelation , en reflexiv och symmetrisk relation:
- Beroenderelation , en ändlig toleransrelation
- Oberoenderelation , komplementet till någon beroenderelation
Släktskapsförhållanden

Generaliseringar

En binär relation i allmänhet behöver inte vara homogen, den definieras som en delmängd R ⊆ X × Y för godtyckliga mängder X och Y .
En finitär relation är en delmängd R ⊆ X ₁ × ... × X _n för något naturligt tal n och godtyckliga mängder X ₁ , ..., X _n , det kallas också en n -är relation.