Diskriminerande av ett algebraiskt talfält

"Brills teorem" omdirigerar hit. För resultatet i algebraisk geometri, se Brill–Noether-satsen .

  En fundamental domän av ringen av heltal i fältet K erhållen från Q genom att angränsa en rot av x ³ − x ² − 2 x + 1. Denna fundamentala domän sitter inuti K ⊗ _Q R . Diskriminanten för K är 49 = 7 ² . Följaktligen är den grundläggande domänens volym 7 och K förgrenas endast vid 7.

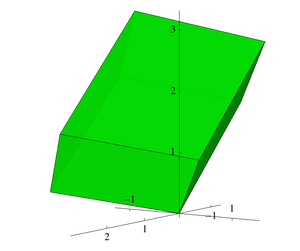
I matematik är diskriminanten för ett algebraiskt talfält en numerisk invariant som, löst sett, mäter storleken på ( ringen av heltal i det) algebraiska talfältet. Mer specifikt är den proportionell mot den kvadratiska volymen av den fundamentala domänen i ringen av heltal , och den reglerar vilka primtal som förgrenas .

Diskriminanten är en av de mest grundläggande invarianterna i ett talfält och förekommer i flera viktiga analytiska formler såsom funktionekvationen för Dedekinds zetafunktion för K och den analytiska klasstalsformeln för K . Ett teorem från Hermite säger att det bara finns ändligt många antal fält av gränsad diskriminant, men att bestämma denna kvantitet är fortfarande ett öppet problem och föremål för aktuell forskning.

Diskriminanten för K kan hänvisas till som den absoluta diskriminanten för K för att skilja den från den relativa diskriminanten för en förlängning K / L av talfält. Det senare är ett ideal i ringen av heltal av L , och liksom den absoluta diskriminanten indikerar det vilka primtal som är förgrenade i K / L . Det är en generalisering av den absoluta diskriminanten som tillåter L att vara större än Q ; i själva verket, när L = Q , är den relativa diskriminanten för K / Q det huvudsakliga idealet för Z som genereras av den absoluta diskriminanten för K.

Definition

Låt K vara ett algebraiskt talfält och låt O _K vara dess ring av heltal . Låt b ₁ , ..., b _n vara en integralbas av O _K (dvs en bas som en Z -modul ), och låt {σ ₁ , ..., σ _n } vara mängden inbäddningar av K i komplexa tal (dvs. injektiv ringhomomorfismer K → C ). Diskriminanten för K är kvadraten på determinanten för n med n matrisen B vars ( i , j )-ingång _{är σi} ( bj ) . Symboliskt,

$\Delta _{K}=\det \left({\begin{array}{cccc}\sigma _{1}(b_{1})&\sigma _{1}(b_{2})& \cdots &\sigma _{1}(b_{n})\\\sigma _{2}(b_{1})&\ddots &&\vdots \\\vdots &&\ddots &\vdots \\\sigma _ {n}(b_{1})&\cdots &\cdots &\sigma _{n}(b_{n})\end{array}}\right)^{2}.$

På motsvarande sätt kan spåret från K till Q användas. _Definiera specifikt spårformen _att vara matrisen vars ( i , j ) -post är TrK _{. / Q} ( bibj ) Denna matris är lika med B ^T B , så diskriminanten för K är determinanten för denna matris.

Diskriminanten för en ordning i K med integralbas b ₁ , ..., b _n definieras på samma sätt.

Exempel

• Kvadratiska talfält : låt d vara ett kvadratfritt heltal , då är diskriminanten för $=\mathbf {Q} ({\sqrt {d}})}$ Δ

$\Delta _{K}=\left\{{\begin{array}{ll}d&{\text{if }}d\equiv 1{\pmod {4}}\\4d&{\text{if }}d\equiv 2,3{\pmod {4}}.\\\end{array}}\right.$

Ett heltal som förekommer som diskriminant för ett kvadratiskt talfält kallas en fundamental diskriminant .

• Cyklotomiska fält : låt n > 2 vara ett heltal, låt ζ _n vara en primitiv n :te rot av enhet och låt K _n = Q (ζ _n ) vara det n :te cyklotomiska fältet. Diskriminanten för K _n ges av

${\displaystyle \Delta _{K_{n}}=(-1)^{\varphi (n)/2}{\frac {n^{\varphi (n )}}{\displaystyle \prod _{p|n}p^{\varphi (n)/(p-1)}}}} där φ ( n ) {\displaystyle \$

varphi $är$ Eulers totientfunktion , och produkten i nämnaren är över primtal p som delar n .

• Potensbaser: I fallet där ringen av heltal har en potensintegralbas , det vill säga kan skrivas som O _K = Z [α], är diskriminanten för K lika med diskriminanten för det minimala polynomet av α. För att se detta kan man välja att integralbasen för O _K ska vara b ₁ = 1, b ₂ = α, b ₃ = α ² , ..., b _n = α ^{n −1} . Då är matrisen i definitionen Vandermonde-matrisen associerad med α _i = σ _i (α), vars determinant i kvadrat är

$\prod _{1 \leq i<j\leq n}(\alpha _{i}-\alpha _{j})^{2}$

vilket är exakt definitionen av diskriminanten för det minimala polynomet.

• Låt K = Q (α) vara talfältet som erhålls genom att angränsa en rot α av polynomet x ³ − x ² − 2 x − 8. Detta är Richard Dedekinds ursprungliga exempel på ett talfält vars ring av heltal inte har en maktbas. En integralbas ges av {1, α, α(α + 1)/2} och diskriminanten för K är −503.
• Upprepade diskriminanter: diskriminanten för ett kvadratiskt fält identifierar det unikt, men detta är i allmänhet inte sant för fält med högre antal. Till exempel finns det två icke-isomorfa kubiska fält av diskriminant 3969. De erhålls genom att angränsa en rot av polynomet x ³ − 21 x + 28 respektive x ³ − 21 x − 35 .

Grundläggande resultat

• Brills sats : Diskriminantens tecken är (−1) ^{r ₂} där r ₂ är antalet komplexa platser för K .
• Ett primtal p ramifierar i K om och endast om p delar Δ _K .
• Stickelbergers sats :

$\Delta _{K}\equiv 0{\text{ eller }}1{\pmod {4}}.$

• Minkowskis gräns : Låt n beteckna graden av förlängningen K / Q och r ₂ antalet komplexa platser av K , sedan

$|\Delta _{K}|^{1/2}\geq {\frac {n^{n}}{n!}}\left({\frac {\pi }{4}}\right )^{r_{2}}\geq {\frac {n^{n}}{n!}}\left({\frac {\pi}{4}}\right)^{n/2}.$

• Minkowskis sats : Om K inte är Q , då |Δ _K | > 1 (detta följer direkt av Minkowski-bunden).
• Hermite–Minkowskis sats : Låt N vara ett positivt heltal. Det finns bara ändligt många (upp till isomorfismer) algebraiska talfält K med |Δ _K | < N . Återigen följer detta av Minkowski bunden tillsammans med Hermites teorem (att det bara finns ändligt många algebraiska talfält med föreskriven diskriminant).

Historia

Richard Dedekind visade att varje talfält har en integrerad grund, vilket gör att han kan definiera diskriminanten för ett godtyckligt talfält.

Definitionen av diskriminant för ett allmänt algebraiskt talfält, K , gavs av Dedekind 1871. Vid denna tidpunkt kände han redan till förhållandet mellan diskriminant och förgrening.

Hermites teorem går före den allmänna definitionen av diskriminanten med Charles Hermite som publicerade ett bevis på det 1857. År 1877 bestämde Alexander von Brill tecknet på diskriminanten. Leopold Kronecker angav Minkowskis teorem för första gången 1882, även om det första beviset gavs av Hermann Minkowski 1891. Samma år publicerade Minkowski sin bindning om diskriminanten. Nära slutet av artonhundratalet Ludwig Stickelberger sin sats om resten av diskriminanten modulo fyra.

Relativ diskriminant

Den ovan definierade diskriminanten kallas ibland för den absoluta diskriminanten av K för att skilja den från den relativa diskriminanten Δ _{K / L} för en förlängning av talfält K / L , vilket är ett ideal i O _L. Den relativa diskriminanten definieras på ett sätt som liknar den absoluta diskriminanten, men måste ta hänsyn till att ideal i O _L kanske inte är principiella och att det kanske inte finns en O _L -bas för O _K . Låt {σ ₁ , ..., σ _n } vara mängden inbäddningar av K i C som är identiteten på L . Om b ₁ , ..., b _n är vilken bas som helst av K över L , låt d ( b ₁ , ..., b _n ) vara kvadraten på determinanten för matrisen n gånger n vars ( i , j ) - posten är σ _i ( b _j ). Då är den relativa diskriminanten för K / L _det ideal som genereras av d ( b ₁ , ..., b _n ) eftersom { b ₁ , ..., bn } varierar över alla integralbaser av K / L . (dvs baser med egenskapen att b _i ∈ O _K för alla i .) Alternativt är den relativa diskriminanten för K / L normen för olika av K / L . När L = Q är den relativa diskriminanten Δ _{K / Q} det huvudsakliga idealet för Z som genereras av den absoluta diskriminanten Δ _K . I ett torn av fält K / L / F är de relativa diskriminanterna relaterade till

$\Delta _{K/F}={\mathcal {N}}_{L/F}\ vänster({\Delta _{K/L}}\right)\Delta _{L/F}^{[K:L]}$

där ${\mathcal {N}}$ anger relativ norm .

Förgrening

Den relativa diskriminanten reglerar förgreningsdata för fältförlängningen K / L . Ett primideal p av L förgrenas i K om, och endast om, det delar den relativa diskriminanten Δ _{K / L} . En förlängning är oförgrenad om, och endast om, diskriminanten är enhetsidealet. Minkowskis bundna ovan visar att det inte finns några icke-triviala oframifierade förlängningar av Q . Fält som är större än Q kan ha oframifierade tillägg: till exempel, för alla fält med klassnummer större än ett, är dess Hilbert-klassfält en icke-trivial oframifierad tillägg.

Rotdiskriminerande

Rotdiskriminanten för ett grad n talfält K definieras av formeln

$\operatorname {rd} _{K}=|\Delta _{K}|^{1/n}.$

Relationen mellan relativa diskriminanter i ett torn av fält visar att rotdiskriminanten inte förändras i en oförgrenad förlängning.

Asymptotiska nedre gränser

Givet icke-negativa rationella tal ρ och σ , inte båda 0, och ett positivt heltal n så att paret ( r ,2 s ) = ( ρn , σn ) är i Z × 2 Z , låt α _n ( ρ , σ ) vara infimum av rd _K som K sträcker sig över grad n talfält med r reella inbäddningar och 2 s komplexa inbäddningar, och låt α ( ρ , σ ) = liminf _{n →∞} α _n ( ρ , σ ). Sedan

$\alpha (\rho ,\sigma )\geq 60.8^{\rho }22.3^{\sigma }$ ,

och den generaliserade Riemann-hypotesen antyder den starkare gränsen

$\alpha (\rho ,\sigma )\geq 215.3^{\rho }44.7^{\sigma }.$

Det finns också en nedre gräns som gäller i alla grader, inte bara asymptotiskt: För helt reella fält är rotdiskriminanten > 14, med 1229 undantag.

Asymptotiska övre gränser

andra sidan kan förekomsten av ett oändligt klassfälttorn ge övre gränser för värdena på α ( ρ , σ ). Till exempel producerar det oändliga klassens fälttorn över Q ( √ - m ) med m = 3·5·7·11·19 fält av godtyckligt stor grad med rotdiskriminant 2 √ m ≈ 296,276, så α (0,1) < 296,276. Med hjälp av tamt förgrenade torn har Hajir och Maire visat att α (1,0) < 954,3 och α (0,1) < 82,2, vilket förbättrar Martinets tidigare gränser.

Förhållande till andra kvantiteter

• När den är inbäddad i ${\displaystyle K\otimes _{\mathbf {Q} }\mathbf {R} } ,$ är volymen för O _{Ks fundamentala domän} ${\displaystyle {\sqrt {|\Delta _{K}|}}} (ibland$ används ett annat mått och den erhållna volymen är $2^{-r_{2}} {\sqrt {|\Delta _{K}|}}$ , där r ₂ är antalet komplexa platser för K ).
• På grund av dess utseende i denna volym, förekommer diskriminanten också i den funktionella ekvationen för Dedekinds zetafunktion av K , och därmed i den analytiska klasstalsformeln och Brauer-Siegel-satsen .
• Den relativa diskriminanten av K / L är Artin-ledaren för den vanliga representationen av Galois-gruppen av K / L . Detta ger en relation till Artin-ledarna för karaktärerna i Galois-gruppen av K / L , kallad dirigentdiskriminerande formel .

Anteckningar

Primära källor

•     Brill, Alexander von (1877), "Ueber die Discriminante" , Mathematische Annalen , 12 (1): 87–89, doi : 10.1007/BF01442468 , JFM 09.0059.02 , MR 15099928 17099928 1709928 27029928 27029928 7209928 72007 retrie. 8-22
• Dedekind, Richard (1871), Vorlesungen über Zahlentheorie von PG Lejeune Dirichlet (2 uppl.), Vieweg , hämtad 2009-08-05
• Dedekind, Richard (1878), "Über den Zusammenhang zwischen der Theorie der Ideale und der Theorie der höheren Congruenzen" , Abhandlungen der Königlichen Gesellschaft der Wissenschaften zu Göttingen , 23 ( 1) , hämtad 2009-08-20
•   Hermite, Charles (1857), "Extrait d'une lettre de MC Hermite à M. Borchardt sur le nombre limité d'irrationalités auxquelles se réduisent les racines des équations à coefficients entiers complexes d'un degré et d'un discriminant donnés" , Crelle's Journal , 1857 (53): 182–192, doi : 10.1515/crll.1857.53.182 , S2CID 120694650 , hämtad 2009-08-20
•   Kronecker, Leopold (1882), "Grundzüge einer arithmetischen Theorie der algebraischen Grössen" , Crelle's Journal , 92 : 1–122, JFM 14.0038.02 , hämtad 2009-08-20
•   Minkowski, Hermann (1891a), "Ueber die positiven quadratischen Formen und über kettenbruchähnliche Algorithmen" , Crelle 's Journal , 1891 (107): 278–297, doi : 10.1515/crll.1891.807 .FMrie .107 ret. 2009-08 -20
•   Minkowski, Hermann (1891b), "Théorèmes d'arithmétiques", Comptes rendus de l'Académie des sciences , 112 : 209–212, JFM 23.0214.01
•   Stickelberger, Ludwig (1897), "Über eine neue Eigenschaft der Diskriminanten algebraischer Zahlkörper", Proceedings of the First International Congress of Mathematicians, Zürich , s. 182–193, JFM 29.0172.03

Sekundära källor

•    Bourbaki, Nicolas (1994). Element i matematikens historia . Översatt av Meldrum, John. Berlin: Springer-Verlag. ISBN 978-3-540-64767-6 . MR 1290116 .
•    Cohen, Henri (1993), A Course in Computational Algebraic Number Theory , Graduate Texts in Mathematics, vol. 138, Berlin, New York: Springer-Verlag , ISBN 978-3-540-55640-4 , MR 1228206
•     Cohen, Henri ; Diaz och Diaz, Francisco; Olivier, Michel (2002), "A Survey of Discriminant Counting", i Fieker, Claus; Kohel, David R. (red.), Algorithmic Number Theory, Proceedings, 5th International Syposium, ANTS-V, University of Sydney, juli 2002 , Lecture Notes in Computer Science, vol. 2369, Berlin: Springer-Verlag, s. 80–94, doi : 10.1007/3-540-45455-1_7 , ISBN 978-3-540-43863-2 , ISSN 0302-9743 , MR 5041
•    Fröhlich, Albrecht ; Taylor, Martin (1993), Algebraisk talteori , Cambridge Studies in Advanced Mathematics, vol. 27, Cambridge University Press , ISBN 978-0-521-43834-6 , MR 1215934
•    Koch, Helmut (1997), Algebraisk talteori , Encycl. Matematik. Sci., vol. 62 (2:a tryckningen av 1:a upplagan), Springer-Verlag , ISBN 3-540-63003-1 , Zbl 0819.11044
•    Narkiewicz, Władysław (2004), Elementär och analytisk teori om algebraiska tal , Springer Monographs in Mathematics (3 uppl.), Berlin: Springer-Verlag, ISBN 978-3-540-21902-6 , MR 2078267
•     Neukirch, Jürgen (1999). Algebraiska Zahlentheorie . Grundlehren der mathematischen Wissenschaften . Vol. 322. Berlin: Springer-Verlag . ISBN 978-3-540-65399-8 . MR 1697859 . Zbl 0956.11021 .
•    Serre, Jean-Pierre (1967), "Local class field theory", i Cassels, JWS ; Fröhlich, Albrecht (red.), Algebraic Number Theory, Proceedings of an instructional conference at University of Sussex, Brighton, 1965 , London: Academic Press, ISBN 0-12-163251-2 , MR 0220701
•      Voight, John (2008), "Uppräkning av totalt reella antal fält av avgränsad rotdiskriminant", i van der Poorten, Alfred J. ; Stein, Andreas (red.), Algoritmisk talteori. Proceedings, 8th International Symposium, ANTS-VIII, Banff, Kanada, maj 2008 , Lecture Notes in Computer Science, vol. 5011, Berlin: Springer- Verlag , s. 268–281, arXiv : 0802.0194 , doi : 10.1007 /978-3-540-79456-1_18 , ISBN 978-3-540-4945 , SMR 3-540-4925 36220 , Zbl 1205.11125
•     Washington, Lawrence (1997), Introduction to Cyclotomic Fields , Graduate Texts in Mathematics, vol. 83 (2:a upplagan), Berlin, New York: Springer-Verlag, ISBN 978-0-387-94762-4 , MR 1421575 , Zbl 0966.11047

Vidare läsning

• Milne, James S. (1998), Algebraic Number Theory , hämtad 2008-08-20