Eulers totient funktion

"φ(n)" omdirigerar hit. För annan användning, se Phi .

Ej att förväxla med Euler-funktion .

De första tusen värdena av φ ( n ) . Punkterna på den översta linjen representerar φ ( p ) när p är ett primtal, vilket är p − 1.

I talteorin räknar Eulers totientfunktion de positiva heltal upp till ett givet heltal n som är relativt primtal till n . Den är skriven med den grekiska bokstaven phi som $\varphi (n)$ eller $\phi (n)$ , och kan också kallas Eulers phi-funktion . Med andra ord är det antalet heltal k i intervallet 1 ≤ k ≤ n för vilket den största gemensamma divisorn gcd( n , k ) är lika med 1. Heltalen k i denna form kallas ibland för totativ av n .

Till exempel är totativen för n = 9 de sex talen 1, 2, 4, 5, 7 och 8. De är alla relativt primtal till 9, men de andra tre talen i detta intervall, 3, 6 och 9 är inte , eftersom gcd(9, 3) = gcd(9, 6) = 3 och gcd(9, 9) = 9 . Därför är φ (9) = 6 . Som ett annat exempel, φ (1) = 1 eftersom för n = 1 är det enda heltal i intervallet från 1 till n 1 själv, och gcd(1, 1) = 1 .

Eulers totientfunktion är en multiplikativ funktion , vilket betyder att om två tal m och n är relativt primtal, då φ ( mn ) = φ ( m ) φ ( n ) . Denna funktion ger ordningen för den multiplikativa gruppen av heltal modulo n ( gruppen av enheter i ringen ${\displaystyle \mathbb {Z} /n\mathbb {Z} } )$ . Det används också för att definiera RSA-krypteringssystemet .

Historia, terminologi och notation

Leonhard Euler introducerade funktionen 1763. Han valde dock inte vid den tiden någon specifik symbol för att beteckna den. I en publikation från 1784 studerade Euler funktionen vidare och valde den grekiska bokstaven π för att beteckna den: han skrev πD för "mängden tal mindre än D , och som inte har någon gemensam divisor med den". Denna definition skiljer sig från den nuvarande definitionen för totientfunktionen vid D = 1 men är i övrigt densamma. Den numera standardnotationen φ ( A ) kommer från Gauss 1801 avhandling Disquisitiones Arithmeticae , även om Gauss inte använde parenteser runt argumentet och skrev φA . Därför kallas det ofta Eulers phi-funktion eller helt enkelt phi-funktionen .

År 1879 myntade JJ Sylvester termen totient för denna funktion, så den kallas också för Eulers totientfunktion , Euler -toienten eller Eulers totient . Jordans totient är en generalisering av Eulers.

Kototienten för n definieras som n − φ ( n ) . Den räknar antalet positiva heltal mindre än eller lika med n som har minst en primtalsfaktor gemensam med n .

Beräknar Eulers totientfunktion

Det finns flera formler för att beräkna φ ( n ) .

Eulers produktformel

Det står

$\varphi (n)=n\prod _{p\mid n}\left(1-{\frac {1}{p} }\höger),$

där produkten ligger över de distinkta primtalen som delar n . (För notation, se Aritmetisk funktion .)

En ekvivalent formulering för $n=p_{1}^{k_{1}}p_{2}^{k_{2}}\cdots p_{ r}^{k_{r}}$ , där $p_{1},p_{2},\ldots ,p_{r}$ är de distinkta primtal som delar n , är:

$$\varphi (n)=p_{1}^{k_{1}-1}(p_{1}{-}1)\,p_{2}^{k_{2}-1}(p_{ 2}{-}1)\cdots p_{r}^{k_{r}-1}(p_{r}{-}1).$$

Beviset för dessa formler beror på två viktiga fakta.

Phi är en multiplikativ funktion

Detta betyder att om gcd( m , n ) = 1 , så är φ ( m ) φ ( n ) = φ ( mn ) . Bevisöversikt: Låt A , B , C vara uppsättningarna av positiva heltal som är coprime till respektive mindre än m , n , mn , så att | A | = φ ( m ) , etc. Sedan finns det en bijektion mellan A × B och C av den kinesiska restsatsen .

Värdet på phi för ett primtalsargument

Om p är primtal och k ≥ 1 , då

$\varphi \left(p^{k}\right)=p^{k}-p^{k-1}=p^{k-1}(p-1)=p^{k}\ vänster(1-{\tfrac {1}{p}}\höger).$

Bevis : Eftersom p är ett primtal är de enda möjliga värdena för gcd( p ^k , m ) 1, p , p ² , ..., p ^{k , och} det gcd( p ^{k ,} m ) > 1 enda sättet att ha är om m är en multipel av p , det vill säga m ∈ { p , 2 p , 3 p , ..., p ^{k − 1} p = p ^k } , och det finns p ^{k − 1} sådana multipler som inte är större än p ^k . Därför är de andra p ^k − p ^{k − 1} talen alla relativt primtal till p ^k .

Bevis på Eulers produktformel

Aritmetikens grundsats säger att om n > 1 finns ett unikt uttryck $n=p_{1}^{k_{1}}p_{ 2}^{k_{2}}\cdots p_{r}^{k_{r}},$ där p ₁ < p ₂ < ... < p _r är primtal och varje k _i ≥ 1 . (Fallet n = 1 motsvarar den tomma produkten.) Att upprepade gånger använda den multiplikativa egenskapen för φ och formeln för φ ( p ^k ) ger

${\begin{array}{rcl}\varphi (n)&=&\varphi (p_{1}^{k_{1}})\,\varphi (p_{2}^{k_{2} })\cdots \varphi (p_{r}^{k_{r}})\\[.1em]&=&p_{1}^{k_{1}-1}(p_{1}-1)\, p_{2}^{k_{2}-1}(p_{2}-1)\cdots p_{r}^{k_{r}-1}(p_{r}-1)\\[.1em] &=&p_{1}^{k_{1}}\left(1-{\frac {1}{p_{1}}}\right)p_{2}^{k_{2}}\left(1- {\frac {1}{p_{2}}}\right)\cdots p_{r}^{k_{r}}\left(1-{\frac {1}{p_{r}}}\right) \\[.1em]&=&p_{1}^{k_{1}}p_{2}^{k_{2}}\cdots p_{r}^{k_{r}}\left(1-{\ frac {1}{p_{1}}}\right)\left(1-{\frac {1}{p_{2}}}\right)\cdots \left(1-{\frac {1}{p_ {r}}}\right)\\[.1em]&=&n\left(1-{\frac {1}{p_{1}}}\right)\left(1-{\frac {1}{ p_{2}}}\right)\cdots \left(1-{\frac {1}{p_{r}}}\right).\end{array}}$

Detta ger båda versionerna av Eulers produktformel.

Ett alternativt bevis som inte kräver den multiplikativa egenskapen använder istället inkluderings -exkluderingsprincipen som tillämpas på mängden $\{1,2,\ldots ,n\}$ , exklusive mängderna av heltal som är delbart med primtallarna.

Exempel

$\varphi (20)=\varphi (2^ {2}5)=20\,(1-{\tfrac {1}{2}})\,(1-{\tfrac {1}{5}})=20\cdot {\tfrac {1}{ 2}}\cdot {\tfrac {4}{5}}=8.$

Med ord: de distinkta primfaktorerna för 20 är 2 och 5; hälften av de tjugo heltal från 1 till 20 är delbara med 2, vilket lämnar tio; en femtedel av dessa är delbara med 5, vilket lämnar åtta tal coprime till 20; dessa är: 1, 3, 7, 9, 11, 13, 17, 19.

Den alternativa formeln använder bara heltal:

$$\varphi (20) =\varphi (2^{2}5^{1})=2^{2-1}(2{-}1)\,5^{1-1}(5{-}1)=2\cdot 1\cdot 1\cdot 4=8.$$

Fouriertransform

Totienten är den diskreta Fouriertransformen av gcd , utvärderad till 1. Let

${\mathcal {F}}\{\mathbf {x} \}[m]=\summa \ gränser _{k=1}^{n}x_{k}\cdot e^{{-2\pi i}{\frac {mk}{n}}}$

där x _k = gcd( k , n ) för k ∈ {1, ..., n } . Sedan

$\varphi (n)={\mathcal {F}}\{\mathbf {x} \}[1]=\summa \limits _{k=1}^{n}\gcd(k,n) e^{-2\pi i{\frac {k}{n}}}.$

Den verkliga delen av denna formel är

$\varphi (n)=\sum \limits _{k=1}^{n}\gcd(k,n)\cos {\tfrac {2\pi k}{n}}.$

Använd till exempel $\cos {\tfrac {\pi }{5}}={\tfrac {{\sqrt {5}}+1}{4}}$ och $\cos {\tfrac {2\pi }{5}}={\tfrac {{\sqrt {5}}-1}{4}}$ :

$${ \begin{array}{rcl}\varphi (10)&=&\gcd(1,10)\cos {\tfrac {2\pi }{10}}+\gcd(2,10)\cos {\tfrac {4\pi }{10}}+\gcd(3,10)\cos {\tfrac {6\pi }{10}}+\cdots +\gcd(10,10)\cos {\tfrac {20\ pi }{10}}\\&=&1\cdot ({\tfrac {{\sqrt {5}}+1}{4}})+2\cdot ({\tfrac {{\sqrt {5}}- 1}{4}})+1\cdot (-{\tfrac {{\sqrt {5}}-1}{4}})+2\cdot (-{\tfrac {{\sqrt {5}}+ 1}{4}})+5\cdot (-1)\\&&+\ 2\cdot (-{\tfrac {{\sqrt {5}}+1}{4}})+1\cdot (- {\tfrac {{\sqrt {5}}-1}{4}})+2\cdot ({\tfrac {{\sqrt {5}}-1}{4}})+1\cdot ({\ tfrac {{\sqrt {5}}+1}{4}})+10\cdot (1)\\&=&4.\end{array}}$$

Till skillnad från Euler-produkten och divisorsummans formel kräver denna inte att man känner till faktorerna för n . Det involverar dock beräkningen av den största gemensamma delaren för n och varje positivt heltal mindre än n , vilket räcker för att tillhandahålla faktoriseringen ändå.

Delningssumma

Fastigheten etablerad av Gauss, att

$\sum _{d\mid n}\varphi (d)=n,$

där summan är över alla positiva delare d av n , kan bevisas på flera sätt. (Se Aritmetisk funktion för notationskonventioner.)

Cd _är att notera att φ ( d ) också är lika med antalet möjliga generatorer av den cykliska gruppen ; specifikt, om C _d = ⟨ g ⟩ med g ^d = 1 , så är g ^k en generator för varje k coprime till d . Eftersom varje element i C _n genererar en cyklisk undergrupp och alla undergrupper C _d ⊆ Cn _. genereras av exakt φ ( d ) element i C _n , följer formeln På motsvarande sätt kan formeln härledas av samma argument som tillämpas på den multiplikativa gruppen av de n :te rötterna av enhet och de primitiva d :te rötterna av enhet .

Formeln kan också härledas från elementär aritmetik. Låt till exempel n = 20 och betrakta de positiva bråken upp till 1 med nämnaren 20:

${\tfrac {1}{20}},\,{\tfrac {2}{20}},\,{\tfrac {3}{20}},\,{\tfrac {4}{20}},\,{\tfrac {5}{20}},\,{\tfrac {6}{20}},\,{\tfrac {7}{20}},\,{\tfrac {8}{20}},\,{\tfrac {9}{20}},\,{\tfrac {10}{20}},\,{\tfrac {11}{20}},\,{\tfrac {12}{20}},\,{\tfrac {13}{20}},\,{\tfrac {14}{20}},\,{\tfrac {15}{20}},\,{\tfrac {16}{20}},\,{\tfrac {17}{20}},\,{\tfrac {18}{20}},\,{\tfrac {19}{20}},\,{\tfrac {20}{20}}.$

Sätt dem i de lägsta termerna:

${\tfrac {1}{20}},\,{\tfrac {1}{10}},\,{\tfrac {3}{20}},\ ,{\tfrac {1}{5}},\,{\tfrac {1}{4}},\,{\tfrac {3}{10}},\,{\tfrac {7}{20}} ,\,{\tfrac {2}{5}},\,{\tfrac {9}{20}},\,{\tfrac {1}{2}},\,{\tfrac {11}{20 }},\,{\tfrac {3}{5}},\,{\tfrac {13}{20}},\,{\tfrac {7}{10}},\,{\tfrac {3} {4}},\,{\tfrac {4}{5}},\,{\tfrac {17}{20}},\,{\tfrac {9}{10}},\,{\tfrac { 19}{20}},\,{\tfrac {1}{1}}$

Dessa tjugo bråk är alla positiva k / d ≤ 1 vars nämnare är divisorerna d = 1, 2, 4, 5, 10, 20 . Bråken med 20 som nämnare är de med täljare relativt primtal till 20, nämligen 1 / 20 , 3 / 20 , 7 / 20 , 9 / 20 , 11 / 20 , 13 / 20 , 17 / 20 , 19 / 20 ; per definition är detta φ (20) fraktioner. På liknande sätt finns det φ (10) bråk med nämnare 10, och φ (5) bråk med nämnare 5, etc. Sålunda delas uppsättningen av tjugo bråk upp i delmängder av storleken φ ( d ) för varje d som delar 20. Ett liknande argument gäller för varje n.

Möbius-inversion applicerad på divisorsummans formel ger

$\varphi (n)=\sum _{d\mid n}\mu \left (d\right)\cdot {\frac {n}{d}}=n\summa _{d\miden n}{\frac {\mu (d)}{d}},$

där μ är Möbius-funktionen , den multiplikativa funktionen definierad av $\mu (p)=-1$ och $\mu (p^{k}) =0$ för varje primtal p och k ≥ 2 . Denna formel kan också härledas från produktformeln genom att multiplicera ut ${\textstyle \prod _{p\mid n}(1-{\frac {1}{p}})}$ för att få ${\textstil \sum _{d\mid n}{\frac {\mu (d)}{d}}.}$

Ett exempel:

$${\begin{aligned}\varphi (20)&=\mu (1)\cdot 20+\mu (2) )\cdot 10+\mu (4)\cdot 5+\mu (5)\cdot 4+\mu (10)\cdot 2+\mu (20)\cdot 1\\[.5em]&=1\ cdot 20-1\cdot 10+0\cdot 5-1\cdot 4+1\cdot 2+0\cdot 1=8.\end{aligned}}$$

Vissa värderingar

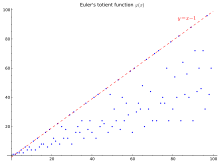
De första 100 värdena (sekvens A000010 i OEIS ) visas i tabellen och diagrammet nedan:

Diagram över de första 100 värdena

φ ( n ) för 1 ≤ n ≤ 100

+	1	2	3	4	5	6	7	8	9	10
0	1	1	2	2	4	2	6	4	6	4
10	10	4	12	6	8	8	16	6	18	8
20	12	10	22	8	20	12	18	12	28	8
30	30	16	20	16	24	12	36	18	24	16
40	40	12	42	20	24	22	46	16	42	20
50	32	24	52	18	40	24	36	28	58	16
60	60	30	36	32	48	20	66	32	44	24
70	70	24	72	36	40	36	60	24	78	32
80	54	40	82	24	64	42	56	40	88	24
90	72	44	60	46	72	32	96	42	60	40

I grafen till höger är den övre linjen y = n − 1 en övre gräns som gäller för alla n utom ett, och uppnås om och endast om n är ett primtal. En enkel nedre gräns är ${\displaystyle \varphi (n)\geq {\sqrt {n/2}}} ,$ som är ganska lös: i själva verket är den nedre gränsen för grafen proportionell till n / logga log n .

Eulers teorem

Huvudartikel: Eulers teorem

Detta anger att om a och n är relativt primtal då

$a^{\varphi (n)}\equiv 1\mod n.$

Det speciella fallet där n är primtal är känt som Fermats lilla sats .

Detta följer av Lagranges teorem och det faktum att φ ( n ) är ordningen för den multiplikativa gruppen av heltal modulo n .

RSA -krypteringssystemet är baserat på detta teorem: det antyder att inversen av funktionen a ↦ a ^e mod n , där e är den (offentliga) krypteringsexponenten, är funktionen b ↦ b ^d mod n , där d , den (privata) ) dekrypteringsexponent, är den multiplikativa inversen av e modulo φ ( n ) . Svårigheten att beräkna φ ( n ) utan att veta faktoriseringen av n är alltså svårigheten att beräkna d : detta är känt som RSA-problemet som kan lösas genom att faktorisera n . Ägaren av den privata nyckeln känner till faktoriseringen, eftersom en privat RSA-nyckel konstrueras genom att välja n som produkten av två (slumpmässigt valda) stora primtal p och q . Endast n offentliggörs, och med tanke på svårigheten att faktorisera stora tal har vi garantin att ingen annan känner till faktoriseringen.

Andra formler

• $a\mid b\implies \varphi (a)\mid \varphi (b)$
• $m\mid \varphi (a^{m}-1)$
• $\varphi (mn)=\varphi (m)\varphi (n)\ cdot {\frac {d}{\varphi (d)}}\quad {\text{där }}d=\operatörsnamn {gcd} (m,n)$

  Särskilt:

  • $\varphi (2m)={\begin{cases}2\varphi (m)&{\text{ om }}m{\text{ är jämnt}}\\\varphi (m)&{\text{ om }}m{\text{ är udda}}\end{case}}$
  • $\varphi \left(n^{m}\right)=n^{m-1}\varphi (n)$
• $\varphi (\operatörsnamn {lcm} (m,n))\cdot \varphi (\operatörsnamn {gcd} (m,n))=\varphi (m)\cdot \varphi (n)$

  Jämför detta med formeln ${\textstil \operatornamn {lcm} (m,n)\cdot \operatornamn {gcd} (m,n)= m\cdot n}$ (se minsta gemensamma multipel ).

• φ ( n ) är jämnt för n ≥ 3 .

  Dessutom, om n har r distinkta udda primtalsfaktorer, 2 ^r | φ ( n )

• För alla a > 1 och n > 6 så att 4 ∤ n finns det en l ≥ 2 n så att l | φ ( a ⁿ − 1) .
• ${\frac {\varphi (n)}{n}}={\frac {\varphi (\operatörsnamn {rad} ( n))}{\operatörsnamn {rad} (n)}}$

  där rad( n ) är radikalen av n (produkten av alla distinkta primtal som delar n ).

• $\sum _{d\mid n}{\frac {\mu ^{2}(d)}{\varphi (d )}}={\frac {n}{\varphi (n)}}$ 
• $\summa _{1\leq k\leq n \atop (k,n)=1} \!\!k={\tfrac {1}{2}}n\varphi (n)\quad {\text{för }}n>1$
• $\sum _{k=1}^{n}\varphi (k)={\tfrac {1}{2}}\left(1+\sum _{k=1 }^{n}\mu (k)\left\lfloor {\frac {n}{k}}\right\rfloor ^{2}\right)={\frac {3}{\pi ^{2}} }n^{2}+O\left(n(\log n)^{\frac {2}{3}}(\log \log n)^{\frac {4}{3}}\right)$ (citerad i)
• $\sum _{k=1}^{n}{\frac {\varphi (k)}{k}}=\sum _{k=1}^{n}{\frac {\mu (k )}{k}}\left\lfloor {\frac {n}{k}}\right\rfloor ={\frac {6}{\pi ^{2}}}n+O\left((\log n )^{\frac {2}{3}}(\log \log n)^{\frac {4}{3}}\right)$ 
• $\sum _{k=1}^{n }{\frac {k}{\varphi (k)}}={\frac {315\,\zeta (3)}{2\pi ^{4}}}n-{\frac {\log n}{ 2}}+O\left((\log n)^{\frac {2}{3}}\right)$ 
• $\sum _{k=1}^{n}{\frac {1}{\varphi (k)}}={\frac {315\,\zeta (3)}{2\pi ^{ 4}}}\left(\log n+\gamma -\sum _{p{\text{primtal}}}{\frac {\log p}{p^{2}-p+1}}\right)+ O\vänster({\frac {(\log n)^{\frac {2}{3}}}{n}}\höger)$ 

  (där γ är Euler-Mascheroni-konstanten ).

• $\sum _{\stackrel {1\leq k\leq n} {\operatörsnamn {gcd} (k,m)=1}}\!\!\!\!1=n{\frac {\varphi (m)}{m}}+O\left(2^{\omega (m)}\right)$

  där m > 1 är ett positivt heltal och ω ( m ) är antalet distinkta primtalsfaktorer för m .

Menons identitet

Huvudartikel: Menons identitet

1965 bevisade P. Kesava Menon

$\sum _{\stackrel {1\leq k\leq n} {\gcd(k,n)=1}}\!\!\!\!\gcd(k-1,n)=\varphi (n)d(n),$

där ₀ d ( n ) = σ ( n ) är antalet divisorer för n .

Genererar funktioner

Dirichlet -serien för φ ( n ) kan skrivas i termer av Riemann zeta-funktionen som:

$\sum _{n=1}^{\infty }{\frac {\varphi (n)}{n ^{s}}}={\frac {\zeta (s-1)}{\zeta (s)}}$

där den vänstra sidan konvergerar för $\Re (s)>2$ .

Lambert -seriens genererande funktion är

$\sum _{n=1}^{\infty }{\frac {\varphi (n)q^ {n}}{1-q^{n}}}={\frac {q}{(1-q)^{2}}}$

som konvergerar för | q | < 1 .

Båda dessa bevisas av elementära seriemanipulationer och formlerna för φ ( n ) .

Tillväxthastighet

är ordningen på φ ( n ) "alltid 'nästan n '."

Först

$\lim \sup {\frac {\varphi (n)}{n}}=1,$

men eftersom n går till oändligheten, för alla δ > 0

${\frac {\varphi (n)}{n^{1-\delta }}}\högerpil \infty .$

Dessa två formler kan bevisas genom att använda lite mer än formlerna för φ ( n ) och divisorsummefunktionen σ ( n ) .

Faktum är att under bevisningen av den andra formeln, ojämlikheten

${\frac {6}{\pi ^{2}}}<{\frac {\varphi (n)\sigma (n) }{n^{2}}}<1,$

sant för n > 1 , är bevisat.

Vi har också

$\lim \inf {\frac {\varphi (n)}{n}}\log \log n=e^{-\gamma }.$

Här är γ Eulers konstant , γ = 0,577215665... , så e ^γ = 1,7810724... och e ^{− γ} = 0,56145948... .

Att bevisa detta kräver inte riktigt primtalssatsen . Eftersom log log n går till oändlighet visar den här formeln det

$\lim \inf {\frac {\varphi (n)}{n}}=0.$

Faktum är att mer är sant.

$\varphi (n)>{\frac {n}{e^{\gamma }\;\log \log n+{\frac {3}{\log \log n}}}}\quad {\text{för }}n>2$

och

$\varphi (n)<{\frac {n}{e^{\gamma }\log \log n}}\quad {\text{för oändligt många }}n.$

Den andra ojämlikheten visades av Jean-Louis Nicolas . Ribenboim säger "Bevismetoden är intressant, eftersom ojämlikheten visas först under antagandet att Riemann- hypotesen är sann, för det andra under det motsatta antagandet."

För den genomsnittliga beställningen har vi

${\ displaystyle \varphi (1)+\varphi (2)+\cdots +\varphi (n)={\frac {3n^{2}}{\pi ^{2}}}+O\left(n(\log n)^{\frac {2}{3}}(\log \log n)^{\frac {4}{3}}\right)\quad {\text{som }}n\högerpil \infty ,}$

på grund av Arnold Walfisz , dess bevis utnyttjar uppskattningar på exponentiella summor på grund av IM Vinogradov och NM Korobov . Genom en kombination av van der Corputs och Vinogradovs metoder har H.-Q. Liu (Om Eulers funktion. Proc. Roy. Soc. Edinburgh Sect. A 146 (2016), nr. 4, 769–775) förbättrade feltermen till

$O\left(n(\log n)^{\frac {2}{3}}(\log \log n )^{\frac {1}{3}}\right)$

(detta är för närvarande den mest kända uppskattningen av denna typ). "Big O " står för en kvantitet som är begränsad av en konstant gånger funktionen av n inom parentesen (vilket är litet jämfört med n ² ).

Detta resultat kan användas för att bevisa att sannolikheten för att två slumpmässigt valda tal är relativt primtal är 6 / π ² .

Förhållandet mellan på varandra följande värden

1950 bevisade Somayajulu

${\begin{aligned}\lim \inf {\frac {\varphi (n+1)}{\varphi (n)}}&=0\quad {\text{and}}\\[5px] \lim \sup {\frac {\varphi (n+1)}{\varphi (n)}}&=\infty .\end{aligned}}$

1954 stärkte Schinzel och Sierpiński detta och bevisade att uppsättningen

$\left\{{\frac {\varphi (n+1)}{\varphi (n)}},\; \;n=1,2,\ldots \right\}$

är tät i de positiva reella talen. De bevisade också att uppsättningen

$\left\{{\frac {\varphi (n)}{n}},\;\;n=1,2,\ldots \ höger\}$

är tät i intervallet (0,1).

Totientnummer

Ett totienttal är ett värde på Eulers totientfunktion: det vill säga ett m för vilket det finns minst ett n för vilket φ ( n ) = m . Valensen eller multipliciteten av ett totient tal m är antalet lösningar till denna ekvation. Ett icke-totient är ett naturligt tal som inte är ett totienttal. Varje udda heltal som överstiger 1 är trivialt en icke-totient. Det finns också oändligt många jämna icke-totienter, och verkligen varje positivt heltal har en multipel som är en jämn nontotient.

Antalet totientnummer upp till en given gräns x är

${\frac {x}{\log x}}e^{{\big (}C+o( 1){\big )}(\log \log \log x)^{2}}$

för en konstant C = 0,8178146... .

är antalet totienttal upp till en given gräns x

${\Big \vert }\{n:\varphi (n)\leq x\}{\Big \vert }= {\frac {\zeta (2)\zeta (3)}{\zeta (6)}}\cdot x+R(x)$

där feltermen R är högst av storleksordningen x / (log x ) ^k för varje positiv k .

Det är känt att multipliciteten av m överstiger m ^δ oändligt ofta för någon δ < 0,55655 .

Fords teorem

Ford (1999) bevisade att för varje heltal k ≥ 2 finns ett totient tal m av multiplicitet k : det vill säga, för vilken ekvationen φ ( n ) = m har exakt k lösningar; detta resultat hade tidigare givits av Wacław Sierpiński , och det hade erhållits som en konsekvens av Schinzels hypotes H . Faktum är att varje mångfald som inträffar gör det oändligt ofta.

Däremot är inget tal m känt med multiplicitet k = 1 . Carmichaels totient funktionsförmodan är påståendet att det inte finns något sådant m .

Perfekta totala siffror

Huvudartikel: Perfekt totientnummer

Ett perfekt totienttal är ett heltal som är lika med summan av dess itererade totienter. Det vill säga att vi tillämpar totientfunktionen på ett tal n , tillämpar den igen på den resulterande totienten, och så vidare, tills talet 1 nås, och adderar den resulterande talföljden; om summan är lika med n så är n ett perfekt totienttal.

Ansökningar

Cyklotomi

Huvudartikel: Konstruerbar polygon

I det sista avsnittet av Disquisitiones bevisar Gauss att en regelbunden n -gon kan konstrueras med rätsida och kompass om φ ( n ) är en potens av 2. Om n är en potens av ett udda primtal säger formeln för totienten dess totient kan vara en potens av två endast om n är en första potens och n − 1 är en potens av 2. Primtal som är en mer än en potens av 2 kallas Fermat-primtal , och endast fem är kända: 3, 5, 17, 257 och 65537. Fermat och Gauss kände till dessa. Ingen har kunnat bevisa om det finns fler.

Således har en vanlig n -gon en rät-och-kompasskonstruktion om n är en produkt av distinkta Fermat-primtal och någon potens av 2. De första få sådana n är

2, 3, 4, 5, 6, 8, 10, 12, 15, 16, 17, 20, 24, 30, 32, 34, 40,... (sekvens A003401 i OEIS ) .

Primtalssats för aritmetiska progressioner

Huvudartikel: Primtalssats § Primtalssats för aritmetiska progressioner

RSA-kryptosystemet

Huvudartikel: RSA (algoritm)

Att sätta upp ett RSA-system innebär att man väljer stora primtal p och q , beräknar n = pq och k = φ ( n ) , och hittar två tal e och d så att ed ≡ 1 (mod k ) . Siffrorna n och e ("krypteringsnyckeln") släpps till allmänheten och d ("dekrypteringsnyckeln") hålls privat.

Ett meddelande, representerat av ett heltal m , där 0 < m < n , krypteras genom att beräkna S = m ^e (mod n ) .

Den dekrypteras genom att beräkna t = Sd ⁽ mod n ) . Eulers sats kan användas för att visa att om 0 < t < n , så är t = m .

Säkerheten för ett RSA-system skulle äventyras om antalet n effektivt kunde faktoriseras eller om φ ( n ) effektivt kunde beräknas utan att faktorisera n .

Olösta problem

Lehmers gissning

Huvudartikel: Lehmers totient problem

Om p är primtal, så är φ ( p ) = p − 1 . 1932 DH Lehmer om det finns några sammansatta tal n så att φ ( n ) delar n − 1 . Inga är kända.

1933 bevisade han att om något sådant n existerar måste det vara udda, kvadratfritt och delbart med minst sju primtal (dvs ω ( n ) ≥ 7 ). 1980 Cohen och Hagis bevisade att n > 10 ²⁰ och att ω ( n ) ≥ 14 . Vidare visade Hagis att om 3 delar n så är n > 10 ^1937042 och ω ( n ) ≥ 298848 .

Carmichaels gissning

Huvudartikel: Carmichaels totala funktionsförmodan

Detta anger att det inte finns något tal n med egenskapen att för alla andra tal m , m ≠ n , φ ( m ) ≠ φ ( n ) . Se Fords teorem ovan.

Som det står i huvudartikeln, om det finns ett enda motexempel till denna gissning, måste det finnas oändligt många motexempel, och det minsta har minst tio miljarder siffror i bas 10.

Riemanns hypotes

Riemanns hypotes är sann om och bara om ojämlikheten

${\frac {n}{\varphi (n)}}<e^{ \gamma }\log \log n+{\frac {e^{\gamma }(4+\gamma -\log 4\pi )}{\sqrt {\log n}}}$

är sant för alla n ≥ p ₁₂₀₅₆₉ # där γ är Eulers konstant och p ₁₂₀₅₆₉ # är produkten av de första 120569 primtalen.

Se även

• Carmichael funktion
• Duffin–Schaeffer gissningar
• Generaliseringar av Fermats lilla teorem
• Mycket sammansatt nummer
• Multiplikativ grupp av heltal modulo n
• Ramanujan summa
• Totient summatorisk funktion
• Dedekind psi-funktion

Anteckningar

Disquisitiones Arithmeticae har översatts från latin till engelska och tyska. Den tyska utgåvan innehåller alla Gauss artiklar om talteori: alla bevis på kvadratisk ömsesidighet, fastställandet av tecknet på Gausssumman, undersökningarna av biquadratisk ömsesidighet och opublicerade anteckningar.

Referenser till Disquisitiones är av formen Gauss, DA, art. nnn .

•   Abramowitz, M .; Stegun, IA (1964), Handbook of Mathematical Functions , New York: Dover Publications , ISBN 0-486-61272-4 . Se avsnitt 24.3.2.
•    Bach, Eric ; Shallit, Jeffrey (1996), Algorithmic Number Theory (Vol I: Efficient Algorithms) , MIT Press Series in the Foundations of Computing, Cambridge, MA: The MIT Press , ISBN 0-262-02405-5 , Zbl 0873.11070
• Dickson, Leonard Eugene, "History Of Theory Of Numbers", vol 1, kapitel 5 "Euler's Function, Generalizations; Farey Series", Chelsea Publishing 1952
•      Ford, Kevin (1999), "The number of solutions of φ( x ) = m ", Annals of Mathematics , 150 (1): 283–311, doi : 10.2307/121103 , ISSN 0003-486X , JSTOR 121103 , 5 MR 6103 , , Zbl 0978.11053 .
•   Gauss, Carl Friedrich (1986), Disquisitiones Arithmeticae (andra, korrigerad upplaga) , översatt av Clarke, Arthur A., ​​New York: Springer , ISBN 0-387-96254-9
•   Gauss, Carl Friedrich (1965), Untersuchungen uber hohere Arithmetik (Disquisitiones Arithmeticae & other papers on number theory) (Andra upplagan) , översatt av Maser, H., New York: Chelsea, ISBN 0-8284-0191-8
•    Graham, Ronald ; Knuth, Donald ; Patashnik, Oren (1994), Concrete Mathematics : a foundation for data science (2nd ed.), Reading, MA: Addison-Wesley, ISBN 0-201-55802-5 , Zbl 0836.00001
•    Guy, Richard K. (2004), Unsolved Problems in Number Theory , Problem Books in Mathematics (3rd ed.), New York, NY: Springer-Verlag , ISBN 0-387-20860-7 , Zbl 1058.11001
•   Hardy, GH ; Wright, EM (1979), An Introduction to the Theory of Numbers (femte upplagan), Oxford: Oxford University Press , ISBN 978-0-19-853171-5
•   Long, Calvin T. (1972), Elementary Introduction to Number Theory (2nd ed.), Lexington: DC Heath and Company , LCCN 77-171950
•   Pettofrezzo, Anthony J.; Byrkit, Donald R. (1970), Elements of Number Theory , Englewood Cliffs: Prentice Hall , LCCN 77-81766
•    Ribenboim, Paulo (1996), The New Book of Prime Number Records (3:e upplagan), New York: Springer , ISBN 0-387-94457-5 , Zbl 0856.11001
•   Sandifer, Charles (2007), Leonhard Eulers tidiga matematik , MAA, ISBN 978-0-88385-559-1
•    Sándor, József; Mitrinović, Dragoslav S.; Crstici, Borislav, red. (2006), Handbook of number theory I , Dordrecht: Springer-Verlag , s. 9–36, ISBN 1-4020-4215-9 , Zbl 1151.11300
•    Sándor, Jozsef; Crstici, Borislav (2004). Handbok i talteori II . Dordrecht: Kluwer Academic. s. 179 –327. ISBN 1-4020-2546-7 . Zbl 1079.11001 .
• Schramm, Wolfgang (2008), "The Fourier transform of functions of the greatest common divisor" , Electronic Journal of Combinatorial Number Theory , A50 (8(1)) .

externa länkar

• "Totient function" , Encyclopedia of Mathematics , EMS Press , 2001 [1994]
• Eulers Phi-funktion och den kinesiska restsatsen – bevis på att φ ( n ) är multiplikativ
• Eulers totalfunktionskalkylator i JavaScript — upp till 20 siffror
• Dineva, Rosica, Euler Totient, Möbius och Divisor-funktionerna
• Plytage, Loomis, Polhill summerar Euler Phi-funktionen