Finit indelningsregel

En perspektivprojektion av en dodekaedrisk tessellation i H ³ . Notera den rekursiva strukturen: varje femhörning innehåller mindre femhörningar, som innehåller mindre femhörningar. Detta är ett exempel på en indelningsregel som härrör från ett ändligt universum (dvs. ett slutet 3-grenrör) .

Inom matematiken är en finit indelningsregel ett rekursivt sätt att dela upp en polygon eller annan tvådimensionell form i mindre och mindre bitar. Indelningsregler på sätt och vis är generaliseringar av vanliga geometriska fraktaler . Istället för att upprepa exakt samma design om och om igen, har de små variationer i varje steg, vilket tillåter en rikare struktur samtidigt som fraktalernas eleganta stil bibehålls. Indelningsregler har använts i arkitektur, biologi och datavetenskap, såväl som i studiet av hyperboliska grenrör . Substitutionsplattor är en väl studerad typ av indelningsregel.

Definition

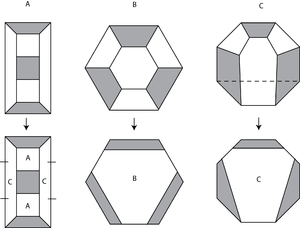
En indelningsregel tar en plattsättning av planet med polygoner och förvandlar den till en ny plattsättning genom att dela upp varje polygon i mindre polygoner. Det är ändligt om det bara finns ändligt många sätt som varje polygon kan dela upp på. Varje sätt att dela upp en bricka kallas en bricka typ . Varje bricktyp representeras av en etikett (vanligtvis en bokstav). Varje bricktyp delas in i mindre bricktyper. Varje kant delas också in enligt ändligt många kanttyper . Finita underindelningsregler kan bara dela upp plattsättningar som är uppbyggda av polygoner märkta med britstyper. Sådana plattsättningar kallas för indelningskomplex för indelningsregeln. Med tanke på vilket indelningskomplex som helst för en indelningsregel kan vi dela upp det om och om igen för att få en sekvens av plattsättningar.

Till exempel har binär underavdelning en bricktyp och en kanttyp:

Eftersom den enda bricktypen är en fyrhörning, kan binär underindelning endast dela in platta som består av fyrhörningar. Detta innebär att de enda indelningskomplexen är plattsättningar med fyrhörningar. Plattläggningen kan vara vanlig , men behöver inte vara:

Här börjar vi med ett komplex av fyra fyrhörningar och delar upp det två gånger. Alla fyrhörningar är typ A-brickor.

Exempel på finita indelningsregler

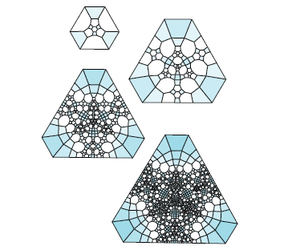
Barycentrisk underavdelning är ett exempel på en indelningsregel med en kanttyp (som delas in i två kanter) och en bricktyp (en triangel som delas in i 6 mindre trianglar). Varje triangulerad yta är ett barycentriskt indelningskomplex.

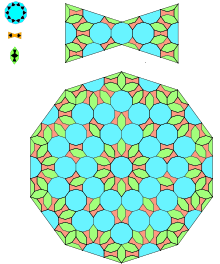
Penrose -plattan kan genereras av en indelningsregel på en uppsättning av fyra bricktyper (de böjda linjerna i tabellen nedan hjälper bara till att visa hur brickorna passar ihop):

namn	Inledande brickor	Generation 1	Generation 2	Generation 3
Halvdrake
Halvdart
Sun
Star

Vissa rationella kartor ger upphov till ändliga indelningsregler. Detta inkluderar de flesta Lattèskartor .

Varje prime, icke-delad alternerande knut eller länkkomplement har en indelningsregel, med vissa brickor som inte delar upp sig, motsvarande gränsen för länkkomplementet. Indelningsreglerna visar hur natthimlen skulle se ut för någon som lever i ett knutkomplement ; eftersom universum sveper sig runt sig själv (dvs. inte bara är anslutet ), skulle en observatör se det synliga universum upprepa sig i ett oändligt mönster. Indelningsregeln beskriver det mönstret.

Indelningsregeln ser olika ut för olika geometrier. Detta är en indelningsregel för trefoil-knuten , som inte är en hyperbolisk knut :

Och detta är indelningsregeln för de borromeiska ringarna , som är hyperbolisk:

I varje enskilt fall skulle indelningsregeln verka på någon kakelsättning av en sfär (dvs natthimlen), men det är lättare att bara rita en liten del av natthimlen, vilket motsvarar att en enskild bricka upprepade gånger delas upp. Detta är vad som händer för trefoil-knuten:

Och för de borromeiska ringarna:

Indelningsregler i högre dimensioner

Indelningsregler kan lätt generaliseras till andra dimensioner. Till exempel används barycentrisk indelning i alla dimensioner. Binär underavdelning kan också generaliseras till andra dimensioner (där hyperkuber delas med varje mittplan), som i beviset för Heine–Borel-satsen .

Rigorös definition

En indelningsregel för fyrtorus. Ytorna på B-brickorna som delar upp kan bara vidröra C-brickorna, och ytorna på B-brickorna som inte bara rör A-brickorna.

En finit indelningsregel $R$ består av följande.

1. Ett ändligt 2-dimensionellt CW-komplex ${\displaystyle S_{R}} ,$ kallat underavdelningskomplexet , med en fixerad cellstruktur så att $S_{R}$ är föreningen av dess slutna 2- celler. Vi antar att det för varje stängd 2-cell ${\tilde {s}}$ av $S_{R}$ finns en CW-struktur $s$ på en stängd 2-skiva så att $s$ har minst två hörn, hörn och kanter av $s$ ingår i $\partial s$ , och den karakteristiska kartan ${ \displaystyle \psi _{s}:s\rightarrow S_{R}}$ som mappas till ${\tilde {s}}$ begränsar till en homeomorfism på varje öppen cell.

2. Ett ändligt tvådimensionellt CW-komplex ${\displaystyle R(S_{R})},$ som är en underavdelning av $\displaystyle S_{R}}$ .

3. En kontinuerlig cellulär karta $\phi _{R}:R(S_{R})\rightarrow S_{R}$ kallas underavdelningskartan , vars begränsning till varje öppen cell är en homeomorfism på en öppen cell.

Varje CW-komplex $s$ i definitionen ovan (med dess givna karakteristiska karta $\psi _{s}$ ) kallas en tile-typ .

Ett $R$ -komplex för en indelningsregel $R$ är ett 2-dimensionellt CW-komplex $X$ som är föreningen av dess slutna 2-celler, tillsammans med en kontinuerlig cellulär karta $f:X\rightarrow S_{R}$ vars begränsning till varje öppen cell är en homeomorfism. Vi kan dela in $X$ i en komplex $R(X)$ genom att kräva att den inducerade kartan $f:R(X )\rightarrow R(S_{R})$ begränsar till en homeomorfism på varje öppen cell. $R(X)$ är återigen ett $R$ -komplex med karta $\phi _{R}\circ f: R(X)\högerpil S_{R}$ . Genom att upprepa denna process får vi en sekvens av uppdelade $R$ -komplex $R^{n}(X)$ med kartor $\phi _{R}^{n}\circ f:R^{n}(X)\högerpil S_{R}$ .

Binär underavdelning är ett exempel:

Indelningskomplexet kan skapas genom att limma ihop de motsatta kanterna av kvadraten, vilket gör indelningskomplexet $S_{R}$ till en torus . Indelningskartan $\phi$ är dubbleringskartan på torus, som lindar meridianen runt sig själv två gånger och longituden runt sig själv två gånger. Detta är en fyrfaldig täckande karta . Planet, kantat av rutor, är ett indelningskomplex för denna indelningsregel, med strukturkartan $f:\mathbb {R} ^{2}\rightarrow R(S_{ R})$ ges av standardtäckningskartan. Under indelning delas varje ruta i planet in i rutor på en fjärdedel av storleken.

Kvasiisometriegenskaper

Historikdiagrammet för den mellersta tredjedelens indelningsregel.

Indelningsregler kan användas för att studera kvasi-isometriegenskaperna hos vissa utrymmen. Givet en indelningsregel $R$ och subdivisionskomplex $X$ , kan vi konstruera en graf som kallas historiegrafen som registrerar indelningsregelns verkan. Grafen består av de dubbla graferna för varje steg ${\displaystyle R^{n}(X)} ,$ tillsammans med kanter som förbinder varje bricka i $R^{n}(X )$ med dess underavdelningar i $R^{n+1}(X)$ .

Historiegrafens kvasi-isometriegenskaper kan studeras med hjälp av indelningsregler. Till exempel är historiegrafen kvasi-isometrisk till hyperboliskt utrymme exakt när indelningsregeln är konform , som beskrivs i Riemanns kombinatoriska kartläggningssats .

Ansökningar

Tillämpningar av indelningsregler.

Ett exempel på en indelningsregel som används i den islamiska konsten känd som girih .

De första tre stegen av Catmull-Clark-indelning av en kub med indelningsyta nedanför.

Bronkiernas förgrening kan modelleras av finita indelningsregler.

Islamiska Girih- plattor i islamisk arkitektur är självliknande plattor som kan modelleras med ändliga indelningsregler. År 2007 Peter J. Lu från Harvard University och professor Paul J. Steinhardt vid Princeton University en artikel i tidskriften Science som antydde att girih plattsättningar hade egenskaper som överensstämmer med självliknande fraktala kvasikristallina plattsättningar som Penrose plattsättningar (presentation 1974, föregångare verk med början omkring 1964) och föregick dem med fem århundraden.

Indelningsytor i datorgrafik använder indelningsregler för att förfina en yta till vilken precisionsnivå som helst. Dessa indelningsytor (som Catmull-Clarks underavdelningsyta ) tar ett polygonnät (den sort som används i 3D-animerade filmer) och förfinar det till ett nät med fler polygoner genom att lägga till och flytta punkter enligt olika rekursiva formler. Även om många punkter förskjuts i denna process, är varje nytt nät kombinatoriskt en underavdelning av det gamla nätet (vilket innebär att för varje kant och vertex på det gamla nätet kan du identifiera en motsvarande kant och vertex i det nya, plus flera kanter till och hörn).

Indelningsregler tillämpades av Cannon, Floyd och Parry (2000) för att studera storskaliga tillväxtmönster för biologiska organismer. Cannon, Floyd och Parry producerade en matematisk tillväxtmodell som visade att vissa system som bestäms av enkla finita indelningsregler kan resultera i objekt (i deras exempel, en trädstam) vars storskaliga form svänger vilt över tiden även om de lokala indelningslagarna kvarstår det samma. Cannon, Floyd och Parry tillämpade också sin modell på analysen av tillväxtmönster hos råttvävnad. De föreslog att den "negativt krökta" (eller icke-euklidiska) naturen hos mikroskopiska tillväxtmönster för biologiska organismer är en av huvudorsakerna till att storskaliga organismer inte ser ut som kristaller eller polyedriska former utan i själva verket i många fall liknar själv- liknande fraktaler . Speciellt föreslog de att en sådan "negativt krökt" lokal struktur manifesteras i starkt veckad och starkt sammankopplad natur av hjärnan och lungvävnaden.

Cannons gissning

Cannon , Floyd och Parry studerade först finita indelningsregler i ett försök att bevisa följande gissningar:

Cannons gissning : Varje Gromov hyperbolisk grupp med en 2-sfär i oändligheten verkar geometriskt på hyperbolisk 3-rymd .

Här är en geometrisk verkan en kokompakt, korrekt diskontinuerlig verkan av isometrier. Denna gissning löstes delvis av Grigori Perelman i hans bevis på geometriseringsförmodan, som säger (delvis) än att någon Gromov hyperbolisk grupp som är en 3-manifold grupp måste agera geometriskt på hyperbolisk 3-rymd. Det återstår dock fortfarande att visa att en Gromov hyperbolisk grupp med en 2-sfär i oändligheten är en 3-manifoldig grupp.

Cannon och Swenson visade att en hyperbolisk grupp med en 2-sfär i oändligheten har en tillhörande indelningsregel. Om denna indelningsregel är konform i en viss mening, kommer gruppen att vara en 3-manifoldig grupp med geometrin hyperboliskt 3-rum.

Kombinatorisk Riemanns kartläggningssats

Indelningsregler ger en sekvens av plattsättningar av en yta, och plattsättningar ger en uppfattning om avstånd, längd och area (genom att låta varje bricka ha längd och area 1). I gränsen kan avstånden som kommer från dessa plattsättningar i någon mening konvergera till en analytisk struktur på ytan. Riemanns kombinatoriska kartläggningssats ger nödvändiga och tillräckliga förutsättningar för att detta ska ske.

Dess uttalande behöver lite bakgrund. En platta $T$ av en ring $R$ (dvs en sluten ring) ger två invarianter, $M_{\sup }(R,T)$ och $m_{\inf }(R,T)$ , kallad approximativa moduli . Dessa liknar den klassiska modulen för en ring . De definieras genom användning av viktfunktioner . En viktfunktion $\rho$ tilldelar ett icke-negativt tal som kallas vikt till varje bricka av $T$ . Varje bana i $R$ kan ges en längd, definierad som summan av vikterna av alla brickor i banan. Definiera höjden $H(\rho )$ för $R$ under $\rho$ för att vara infimum av längden på alla möjliga banor som förbinder den inre gränsen för ${\ displaystyle R}$ till den yttre gränsen. Omkretsen $C(\rho )$ av R $\displaystyle R}$ under $\rho$ är infimum av längden på alla möjliga banor som cirkulerar ringen (dvs inte nullhomotopic i R) . Arean $A(\rho )$ av $R$ under $\rho$ definieras som summan av kvadraterna av alla vikter i $\displaystyle R}$ { . Definiera sedan

$M_{\sup }(R,T)=\sup {\frac {H(\rho )^{2}}{ A(\rho )}},$

$m_{\inf }(R,T)=\inf {\frac {A(\rho )}{C(\rho )^{2}}}.$

Observera att de är invarianta under skalning av måtten.

En sekvens $T_{1},T_{2},\ldots$ av plattsättningar är konform ( ${\displaystyle K})$ om mesh närmar sig 0 och:

1. För varje ring $R$ , de ungefärliga modulerna $M_{\sup }(R,T_{i})$$\displaystyle m_{\inf }(R,T_{i})}$ inf , för alla $i$ tillräckligt stora, ligger i ett enda intervall av formen $[r,Kr]$ ; och
2. Givet en punkt $x$ i ytan, en grannskap $N$ av $x$ och ett heltal $I$ , finns det en ring $R$ i $N\smallsetminus \{x\}$ som skiljer x från komplementet till $N$ , så att för alla stora $i$ den ungefärliga modulen för $R$ är alla större än $I$ .

Uttalande av teorem

Om en sekvens $T_{1},T_{2},\ldots$ av plattsättningar av en yta är konform ( ${\displaystyle K} )$ i ovanstående mening, så finns det en konform struktur på ytan och en konstant $K'$ endast beroende på $K$ där de klassiska modulerna och approximativa modulerna (från $T_{i}$ för $i$ tillräckligt stor) av en given ring är $K'$ -jämförbara, vilket betyder att de ligger i ett enda intervall $[r,K'r]$ .

Konsekvenser

Riemanns kombinatoriska avbildningssats antyder att en grupp $G$ verkar geometriskt på $\mathbb {H} ^{3}$ om och endast om den är Gromov hyperbolisk, den har en sfär i oändligheten, och den naturliga indelningsregeln på sfären ger upphov till en sekvens av plattsättningar som är konform i ovanstående mening. Således skulle Cannons gissning vara sann om alla sådana indelningsregler var konforma.

externa länkar

• Bill Floyds forskningssida . Den här sidan innehåller de flesta forskningsartiklar av Cannon, Floyd och Parry om indelningsregler, samt ett galleri med indelningsregler.