Trunkerade 7-simplex

Ortogonala projektioner i A ₇ Coxeter-plan
7-simplex	Trunkerad 7-simplex
Bitruncated 7-simplex	Tritrunkerad 7-simplex

I sjudimensionell geometri är en trunkerad 7-simplex en konvex enhetlig 7-polytop , som är en trunkering av den vanliga 7-simplexen .

Det finns unika 3 grader av trunkering. Vertices av trunkering 7-simplex är placerade som par på kanten av 7-simplex. Vertices av bitruncated 7-simplex är belägna på de triangulära ytorna av 7-simplex. Vertices av det tritrunkerade 7-simplexet är belägna inuti de tetraedriska cellerna i 7-simplexet.

Trunkerad 7-simplex

Trunkerad 7-simplex
Typ	enhetlig 7-polytop
Schläfli symbol	t{3,3,3,3,3,3}
Coxeter-Dynkin diagram
6-ansikten	16
5-ansikten
4-ansikten
Celler	350
Ansikten	336
Kanter	196
Vertices	56
Vertex figur	( )v{3,3,3,3}
Coxeter grupper	A ₇ , [3,3,3,3,3,3]
Egenskaper	konvex , Vertex-transitiv

I sjudimensionell geometri är en trunkerad 7-simplex en konvex enhetlig 7-polytop , som är en trunkering av den vanliga 7-simplexen .

Alternativa namn

Trunkerad octaexon (Akronym: toc) (Jonathan Bowers)

Koordinater

Topparna av det trunkerade 7-simplexet kan enklast placeras i 8-rum som permutationer av (0,0,0,0,0,0,1,2). Denna konstruktion är baserad på aspekter av det trunkerade 8-ortoplexet .

Bilder

ortografiska projektioner
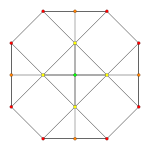
Ett _k Coxeter-plan	En ₇	En ₆	En ₅
Graf
Dihedral symmetri	[8]	[7]	[6]
Ett _k Coxeter-plan	A ₄	A ₃	A ₂
Graf
Dihedral symmetri	[5]	[4]	[3]

Bitruncated 7-simplex

Bitruncated 7-simplex
Typ	enhetlig 7-polytop
Schläfli symbol	2t{3,3,3,3,3,3}
Coxeter-Dynkin diagram
6 ansikten
5 ansikten
4 ansikten
Celler
ansikten
Kanter	588
Vertices	168
Vertex figur	{ }v{3,3,3}
Coxeter grupper	A ₇ , [3,3,3,3,3,3]
Egenskaper	konvex , Vertex-transitiv

Alternativa namn

Bitruncated octaexon (akronym: bittoc) (Jonathan Bowers)

Koordinater

Hörnen för den bitrunkerade 7-simplexen kan enklast placeras i 8-mellanrum som permutationer av (0,0,0,0,0,1,2,2). Denna konstruktion är baserad på aspekter av det bitrunkerade 8-ortoplexet .

Bilder

ortografiska projektioner
Ett _k Coxeter-plan	En ₇	En ₆	En ₅
Graf
Dihedral symmetri	[8]	[7]	[6]
Ett _k Coxeter-plan	A ₄	A ₃	A ₂
Graf
Dihedral symmetri	[5]	[4]	[3]

Tritrunkerad 7-simplex

Tritrunkerad 7-simplex
Typ	enhetlig 7-polytop
Schläfli symbol	3t{3,3,3,3,3,3}
Coxeter-Dynkin diagram
6 ansikten
5 ansikten
4 ansikten
Celler
ansikten
Kanter	980
Vertices	280
Vertex figur	{3}v{3,3}
Coxeter grupper	A ₇ , [3,3,3,3,3,3]
Egenskaper	konvex , Vertex-transitiv

Alternativa namn

Tritruncated octaexon (akronym: tattoc) (Jonathan Bowers)

Koordinater

Topparna av det tritrunkerade 7-simplexet kan enklast placeras i 8-rum som permutationer av (0,0,0,0,1,2,2,2). Denna konstruktion är baserad på aspekter av det tritrunkerade 8-ortoplexet .

Bilder

ortografiska projektioner
Ett _k Coxeter-plan	En ₇	En ₆	En ₅
Graf
Dihedral symmetri	[8]	[7]	[6]
Ett _k Coxeter-plan	A ₄	A ₃	A ₂
Graf
Dihedral symmetri	[5]	[4]	[3]

Besläktade polytoper

Dessa tre polytoper är från en uppsättning av 71 enhetliga 7-polytoper med A ₇ symmetri.

A7 polytoper
t₀	t ₁	t ₂	t ₃	t _0,1	t _0,2	t _1,2	t _0,3
t _1,3	t _2,3	t _0,4	t _1,4	t _2,4	t _0,5	t _1,5	t _0,6
t _0,1,2	t _0,1,3	t _0,2,3	t _1,2,3	t _0,1,4	t _0,2,4	t _1,2,4	t _0,3,4
t _1,3,4	t _2,3,4	t _0,1,5	t _0,2,5	t _1,2,5	t _0,3,5	t _1,3,5	t _0,4,5
t _0,1,6	t _0,2,6	t _0,3,6	t _0,1,2,3	t _0,1,2,4	t _0,1,3,4	t _0,2,3,4	t _1,2,3,4
t _0,1,2,5	t _0,1,3,5	t _0,2,3,5	t _1,2,3,5	t _0,1,4,5	t _0,2,4,5	t _1,2,4,5	t _0,3,4,5
t _0,1,2,6	t _0,1,3,6	t _0,2,3,6	t _0,1,4,6	t _0,2,4,6	t _0,1,5,6	t _0,1,2,3,4	t _0,1,2,3,5
t _0,1,2,4,5	t _0,1,3,4,5	t _0,2,3,4,5	t _1,2,3,4,5	t _0,1,2,3,6	t _0,1,2,4,6	t _0,1,3,4,6	t _0,2,3,4,6
t _0,1,2,5,6	t _0,1,3,5,6	t _0,1,2,3,4,5	t _0,1,2,3,4,6	t _0,1,2,3,5,6	t _0,1,2,4,5,6	t _{0,1,2,3,4,5,6}

Se även

Lista över A7 polytoper

Anteckningar

HSM Coxeter :
- HSM Coxeter, Regular Polytopes , 3:e upplagan, Dover New York, 1973
- Kaleidoscopes: Selected Writings of HSM Coxeter , redigerad av F. Arthur Sherk, Peter McMullen, Anthony C. Thompson, Asia Ivic Weiss, Wiley-Interscience Publication, 1995, ISBN 978-0-471-01003-6 [1]
  - (Papper 22) HSM Coxeter, Regular and Semi Regular Polytopes I , [Math. Zeit. 46 (1940) 380-407, MR 2,10]
  - (Papper 23) HSM Coxeter, Regular and Semi-Regular Polytopes II , [Math. Zeit. 188 (1985) 559-591]
  - (Papper 24) HSM Coxeter, Regular and Semi-Regular Polytopes III , [Math. Zeit. 200 (1988) 3-45]
Norman Johnson Uniform Polytopes , Manuscript (1991)
- NW Johnson: Theory of Uniform Polytopes and Honeycombs , Ph.D.
Klitzing, Richard. "7D enhetliga polytoper (polyexa)" . x3x3o3o3o3o3o - toc, o3x3x3o3o3o3o - roc, o3o3x3x3o3o3o - tattoc

externa länkar

Grundläggande konvexa regelbundna och enhetliga polytoper i dimensionerna 2–10
Familj	A _n	B _n	I ₂ (p) / D _n	E ₆ / E ₇ / E ₈ / F ₄ / G ₂	H _n
Vanlig polygon	Triangel	Fyrkant	p-gon	Sexhörning	Pentagon
Uniform polyeder	Tetraeder	Oktaeder • Kub	Demicube		Dodekaeder • Ikosaeder
Uniform polychoron	Pentachoron	16-celler • Tesseract	Demitesseract	24-celler	120-celler • 600-celler
Uniform 5-polytop	5-simplex	5-ortoplex • 5-kub	5-demikub
Uniform 6-polytop	6-simplex	6-ortoplex • 6-kub	6-demikub	1 ₂₂ • 2 ₂₁
Uniform 7-polytop	7-simplex	7-ortoplex • 7-kub	7-demikub	1 ₃₂ • 2 ₃₁ • 3 ₂₁
Uniform 8-polytop	8-simplex	8-ortoplex • 8-kub	8-demikub	1 ₄₂ • 2 ₄₁ • 4 ₂₁
Uniform 9-polytop	9-simplex	9-ortoplex • 9-kub	9-demikub
Uniform 10-polytop	10-simplex	10-ortoplex • 10-kub	10-demikub
Uniform n - polytop	n - simplex	n - ortoplex • n - kub	n - demikub	1 _k2 • 2 _k1 • k ₂₁	n - femkantig polytop
Ämnen: Polytopfamiljer • Vanlig polytop • Lista över vanliga polytoper och sammansättningar