Position (geometri)

Radievektor

{\vec {r}}

representerar positionen för en punkt

\mathrm {P} (x,y,z)

med avseende på origo O I kartesiskt koordinatsystem

{\vec {r}}=x\,{\hat {e}}_{x}+y\ ,{\hat {e}}_{y}+z\,{\hat {e}}_{z}

.

Inom geometrin är en positions- eller positionsvektor , även känd som positionsvektor eller radievektor , en euklidisk vektor som representerar positionen för en punkt P i rymden i förhållande till ett godtyckligt referensursprung O. Vanligtvis betecknad x , r eller s , det motsvarar det raka linjesegmentet från O till P . Det är med andra ord förskjutning eller översättning som mappar ursprunget till P :

\mathbf {r} ={\överhögerpil {OP}}

Termen "positionsvektor" används mestadels inom differentialgeometri , mekanik och ibland vektorkalkyl .

Detta används ofta i tvådimensionellt eller tredimensionellt utrymme , men kan lätt generaliseras till euklidiska utrymmen och affina utrymmen av vilken dimension som helst .

Relativ position

Den relativa positionen för en punkt Q med avseende på punkt P är den euklidiska vektorn som är resultatet av subtraktionen av de två absoluta positionsvektorerna (var och en med avseende på origo):

\Delta \mathbf {r} =\mathbf {s} -\mathbf {r} ={\overrightarrow {PQ}}

där $\mathbf {s} ={\överhögerpil {OQ}}$ .

Den relativa riktningen mellan två punkter är deras relativa position normaliserad som en enhetsvektor :

\Delta \mathbf {\hat {r}} =\Delta \mathbf {r} /\|\Delta \mathbf {r} \|

där nämnaren är avståndet mellan de två punkterna, $\|\Delta \mathbf {r} \|$ .

Definition

Tre dimensioner

Rymdkurva i 3D. Positionsvektorn r parametriseras av en skalär t . Vid r = a är den röda linjen tangenten till kurvan och det blå planet är normalt mot kurvan.

I tre dimensioner kan vilken uppsättning tredimensionella koordinater som helst och deras motsvarande basvektorer användas för att definiera platsen för en punkt i rymden – vilken som är den enklaste för uppgiften kan användas.

Vanligtvis använder man det välbekanta kartesiska koordinatsystemet , eller ibland sfäriska polära koordinater , eller cylindriska koordinater :

{\begin{aligned}\mathbf {r} (t)&\equiv \mathbf {r} (x,y,z)\equiv x(t)\mathbf {\hat {e}} _{x }+y(t)\mathbf {\hat {e}} _{y}+z(t)\mathbf {\hat {e}} _{z}\\&\equiv \mathbf {r} (r, \theta ,\phi )\equiv r(t)\mathbf {\hat {e}} _{r}{\big (}\theta (t),\phi (t){\big )}\\&\ ekvivalent \mathbf {r} (r,\phi ,z)\equiv r(t)\mathbf {\hat {e}} _{r}{\big (}\phi (t){\big )}+z (t)\mathbf {\hat {e}} _{z},\\\end{aligned}}

där t är en parameter , på grund av deras rektangulära eller cirkulära symmetri. Dessa olika koordinater och motsvarande basvektorer representerar samma positionsvektor. Mer generella kurvlinjära koordinater skulle kunna användas istället och finns i sammanhang som kontinuummekanik och generell relativitetsteori (i det senare fallet behöver man en extra tidskoordinat).

n dimensioner

Linjär algebra möjliggör abstraktion av en n -dimensionell positionsvektor. En positionsvektor kan uttryckas som en linjär kombination av basvektorer :

\mathbf {r} =\sum _{i=1}^{n}x_{i}\mathbf {e} _{i}=x_{1}\mathbf {e} _{1}+x_ {2}\mathbf {e} _{2}+\dotsb +x_{n}\mathbf {e} _{n}.

Mängden av alla positionsvektorer bildar positionsrymd (ett vektorrum vars element är positionsvektorerna), eftersom positioner kan adderas ( vektoraddition ) och skalas i längd ( skalär multiplikation ) för att erhålla ytterligare en positionsvektor i rummet. Begreppet "rymd" är intuitivt, eftersom varje x _i ( i = 1, 2, …, n ) kan ha vilket värde som helst, definierar samlingen av värden en punkt i rymden.

Positionsutrymmets dimension är n ( även betecknad dim( R ) = n ). Koordinaterna _för vektorn r med avseende på basvektorerna ei är x _i . Koordinatvektorn bildar koordinatvektorn eller n - tupeln ( x 1 _, x 2 _, …, x _n ).

Varje koordinat x _i kan parametriseras med ett antal parametrar t . En parameter xi ₍ ( t ₎ skulle beskriva en krökt 1D-bana, två parametrar _xi (t1, t2 _- ) beskriver _en krökt 2D-yta, tre _xi t1, t2 _3D , t3 ₎ beskriver en krökt volym av utrymme och så vidare.

Det linjära spannet för en basmängd B = { e ₁ , e ₂ , …, e _n } är lika med positionsutrymmet R , betecknat span( B ) = R .

Ansökningar

Differentialgeometri

Positionsvektorfält används för att beskriva kontinuerliga och differentierbara rymdkurvor, i vilket fall den oberoende parametern inte behöver vara tid, utan kan vara (t.ex.) kurvans båglängd.

Mekanik

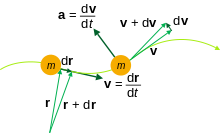
I alla rörelseekvationer är positionsvektorn r ( t ) vanligtvis den mest eftertraktade storheten eftersom denna funktion definierar rörelsen för en partikel (dvs en punktmassa ) – dess läge i förhållande till ett givet koordinatsystem någon gång t .

För att definiera rörelse i termer av position, kan varje koordinat parametriseras av tid; eftersom varje successivt tidsvärde motsvarar en sekvens av successiva rumsliga platser som ges av koordinaterna, kontinuumgränsen för många successiva platser en väg som partikeln spårar.

I fallet med en dimension har positionen bara en komponent, så den degenererar effektivt till en skalär koordinat. Det kan till exempel vara en vektor i x -riktningen eller den radiella r- riktningen. Motsvarande beteckningar inkluderar

\mathbf {x} \equiv x\equiv x(t),\quad r\equiv r(t),\quad s\equiv s(t).

Derivat av position

Kinematiska storheter av en klassisk partikel: massa m , position r , hastighet v , acceleration a

För en positionsvektor r som är en funktion av tiden t , kan tidsderivatorna beräknas med avseende på t . Dessa derivat har gemensam användning i studiet av kinematik , kontrollteori , ingenjörsvetenskap och andra vetenskaper.

Hastighet: ${\displaystyle \mathbf {v} ={\frac {\mathrm {d} \mathbf {r} }{\mathrm {d} t}},} där d$; r är en oändligt liten förskjutning (vektor) .
Acceleration: $\mathbf {a} ={\frac {\mathrm {d} \mathbf {v} }{\mathrm {d} t}}={\frac {\mathrm {d} ^{2}\mathbf { r} }{\mathrm {d} t^{2}}}.$
Jerk: $\mathbf {j} ={\frac {\mathrm {d} \mathbf {a} }{\mathrm {d} t}}={\frac {\mathrm {d} ^{2}\mathbf { v} }{\mathrm {d} t^{2}}}={\frac {\mathrm {d} ^{3}\mathbf {r} }{\mathrm {d} t^{3}}}.$

Dessa namn för den första, andra och tredje derivatan av position används ofta i grundläggande kinematik. I förlängningen kan de högre ordningens derivator beräknas på ett liknande sätt. Studie av dessa högre ordningens derivator kan förbättra approximationer av den ursprungliga förskjutningsfunktionen. Sådana termer av högre ordning krävs för att korrekt representera förskjutningsfunktionen som summan av en oändlig sekvens, vilket möjliggör flera analytiska tekniker inom teknik och fysik.

Se även

Anteckningar

^ Termen förskjutning används främst inom mekanik, medan translation används inom geometri.
^ Keller, F. J, Gettys, WE et al. (1993), sid 28-29
^ Riley, KF; Hobson, MP; Bence, SJ (2010). Matematiska metoder för fysik och teknik . Cambridge University Press. ISBN 978-0-521-86153-3 .
^ Lipschutz, S.; Lipson, M. (2009). Linjär algebra . McGraw Hill. ISBN 978-0-07-154352-1 .
^ Stewart, James (2001). "§2.8. Derivatan som en funktion". Calculus (2:a uppl.). Brooks/Cole. ISBN 0-534-37718-1 .

Keller, F.J, Gettys, WE et al. (1993). "Fysik: Klassiskt och modernt" 2nd ed. McGraw Hill Publishing.

externa länkar

Media relaterade till Position (geometri) på Wikimedia Commons

[1] Termen förskjutning används främst inom mekanik, medan translation används inom geometri.

[phys_keller-2] Keller, F. J, Gettys, WE et al. (1993), sid 28-29

[3] Riley, KF; Hobson, MP; Bence, SJ (2010). Matematiska metoder för fysik och teknik . Cambridge University Press. ISBN 978-0-521-86153-3 .

[4] Lipschutz, S.; Lipson, M. (2009). Linjär algebra . McGraw Hill. ISBN 978-0-07-154352-1 .

[stewart-5] Stewart, James (2001). "§2.8. Derivatan som en funktion". Calculus (2:a uppl.). Brooks/Cole. ISBN 0-534-37718-1 .