Vågplatta

Elektriskt fält parallellt med den optiska axeln

Elektriskt fält vinkelrätt mot axeln

Det kombinerade fältet

Linjärt polariserat ljus som kommer in i en halvvågsplatta kan lösas upp i två vågor, parallella och vinkelräta mot vågplattans optiska axel. I plattan utbreder sig den parallella vågen något långsammare än den vinkelräta. På den bortre sidan av plattan är den parallella vågen exakt hälften av en våglängd fördröjd i förhållande till den vinkelräta vågen, och den resulterande kombinationen är en spegelbild av ingångspolarisationstillståndet (relativt den optiska axeln).

En vågplatta eller retarder är en optisk anordning som ändrar polarisationstillståndet för en ljusvåg som färdas genom den. Två vanliga typer av vågplattor är halvvågsplattan , som skiftar polarisationsriktningen för linjärt polariserat ljus, och kvartsvågsplattan , som omvandlar linjärt polariserat ljus till cirkulärt polariserat ljus och vice versa. En kvartsvågsplatta kan också användas för att producera elliptisk polarisering.

Vågplattor är konstruerade av ett dubbelbrytande material (såsom kvarts eller glimmer , eller till och med plast), för vilket brytningsindex är annorlunda för ljus linjärt polariserat längs den ena eller den andra av två vissa vinkelräta kristallaxlar. Beteendet hos en vågplatta (det vill säga om det är en halvvågsplatta, en kvartsvågsplatta etc.) beror på kristallens tjocklek, ljusets våglängd och variationen av brytningsindex. Genom lämpligt val av förhållandet mellan dessa parametrar är det möjligt att införa en kontrollerad fasförskjutning mellan de två polarisationskomponenterna i en ljusvåg, och därigenom ändra dess polarisation.

En vanlig användning av vågplattor - särskilt den känsliga nyansen (helvågs) och kvartsvågsplattorna - är inom optisk mineralogi . Tillsats av plattor mellan polarisatorerna i ett petrografiskt mikroskop gör den optiska identifieringen av mineraler i tunna sektioner av bergarter lättare, i synnerhet genom att tillåta deduktion av formen och orienteringen av de optiska indikationerna inom de synliga kristallsektionerna. Denna inriktning kan tillåta diskriminering mellan mineraler som annars verkar mycket lika i planpolariserat och korspolariserat ljus.

Funktionsprinciper

En våg i en enaxlig kristall kommer att separeras i två komponenter, en parallell och en vinkelrät mot den optiska axeln, som kommer att ackumulera fas med olika hastigheter. Detta kan användas för att manipulera vågens polariseringstillstånd.

En vågplatta monterad i ett roterande fäste

En vågplatta fungerar genom att skifta fasen mellan två vinkelräta polarisationskomponenter i ljusvågen. En typisk vågplatta är helt enkelt en dubbelbrytande kristall med en noggrant vald orientering och tjocklek. Kristallen skärs till en platta, med snittets orientering vald så att optiska axel är parallell med plattans ytor. Detta resulterar i två axlar i snittets plan: den ordinarie axeln , med brytningsindex n _o , och den extraordinära axeln , med brytningsindex n _e . Den ordinarie axeln är vinkelrät mot den optiska axeln. Den extraordinära axeln är parallell med den optiska axeln. För en ljusvåg som normalt infaller på plattan rör sig polarisationskomponenten längs den ordinarie axeln genom kristallen med en hastighet v _o = c / n _o , medan polarisationskomponenten längs den extraordinära axeln färdas med en hastighet v _e = c / n _e . Detta leder till en fasskillnad mellan de två komponenterna när de lämnar kristallen. När n _e < n _o , som i kalcit , kallas den extraordinära axeln för den snabba axeln och den ordinarie axeln kallas den långsamma axeln . För n _e > n _o är situationen den omvända.

Beroende på kristallens tjocklek kommer ljus med polarisationskomponenter längs båda axlarna att framträda i ett annat polarisationstillstånd. Vågplattan kännetecknas av mängden relativ fas, Γ, som den ger de två komponenterna, vilket är relaterat till dubbelbrytningen Δ n och tjockleken L av kristallen med formeln

\Gamma ={\frac {2\pi \,\Delta n\,L}{\lambda _{0}}},

₀ där λ är ljusets vakuumvåglängd.

Vågplattor i allmänhet, såväl som polarisatorer , kan beskrivas med Jones matrisformalism, som använder en vektor för att representera ljusets polarisationstillstånd och en matris för att representera den linjära transformationen av en vågplatta eller polarisator.

₀ Även om dubbelbrytningen Δn kan variera något på grund av dispersion , är detta försumbart jämfört med variationen i fasskillnad enligt ljusets våglängd på grund av den fasta vägskillnaden (λ i nämnaren i ekvationen ovan). Vågplattor tillverkas således för att fungera för ett visst intervall av våglängder. Fasvariationen kan minimeras genom att stapla två vågplattor som skiljer sig en liten mängd i tjocklek rygg mot rygg, med den enas långsamma axel längs den andras snabba axel. Med denna konfiguration kan den relativa fasen som överförs vara, för fallet med en kvartsvågsplatta, en fjärdedel av en våglängd snarare än tre fjärdedelar eller en fjärdedel plus ett heltal. Detta kallas en nollordningens vågplatta .

För en enda vågplatta introducerar ändring av ljusets våglängd ett linjärt fel i fasen. Vågplattans lutning går in via en faktor 1/cos θ (där θ är lutningsvinkeln) in i väglängden och alltså endast kvadratiskt in i fasen. För den extraordinära polarisationen ändrar lutningen också brytningsindexet till det ordinarie via en faktor på cos θ, så kombinerat med väglängden är fasförskjutningen för det extraordinära ljuset på grund av lutningen noll.

En polarisationsoberoende fasförskjutning av noll ordning behöver en platta med en tjocklek på en våglängd. För kalcit ändras brytningsindexet med första decimalen, så att en verklig nollordningsplatta är tio gånger så tjock som en våglängd. För kvarts och magnesiumfluorid ändras brytningsindexet med andra decimalen och sanna nollordningens plattor är vanliga för våglängder över 1 μm.

Typer av tallrikar

Halvvågsplatta

En våg som passerar genom en halvvågsplatta

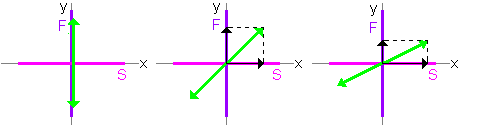
₀ För en halvvågsplatta väljs förhållandet mellan L , Δ n och λ så att fasförskjutningen mellan polarisationskomponenterna är Γ = π. Antag nu att en linjärt polariserad våg med polarisationsvektor $\mathbf {\hat {p}}$ infaller på kristallen. Låt θ beteckna vinkeln mellan $\mathbf {\hat {p}}$ och $\mathbf {\hat {f}}$ , där $\mathbf {\hat { f}}$ är vektorn längs vågplattans snabba axel. Låt z beteckna vågens utbredningsaxel. Det elektriska fältet för den infallande vågen är

{\ displaystyle \mathbf {E} \,\mathrm {e} ^{i(kz-\omega t)}=E\,\mathbf {\hat {p}} \,\mathrm {e} ^{i(kz- \omega t)}=E(\cos \theta \,\mathbf {\hat {f}} +\sin \theta \,\mathbf {\hat {s}} )\mathrm {e} ^{i(kz -\omega t)},}

där $\mathbf {\hat {s}}$ ligger längs vågplattans långsamma axel. Effekten av halvvågsplattan är att introducera en fasförskjutningsterm e ^{i Γ} = e ^{i π} = −1 mellan vågens f- och s- komponenter, så att vågen när den lämnar kristallen nu ges av

E(\cos \theta \,\mathbf {\hat {f}} -\sin \theta \,\mathbf {\hat {s}} )\mathrm {e} ^{i(kz-\omega t)}=E[\cos(-\theta )\mathbf {\hat {f}} +\sin(-\theta )\mathbf {\hat {s}} ]\mathrm {e} ^{i(kz -\omega t)}.

Om $\mathbf {\hat {p}} '$ anger polarisationsvektorn för vågen som lämnar vågplattan, så visar detta uttryck att vinkeln mellan $\mathbf {\hat {p }} '$ och $\mathbf {\hat {f}}$ är −θ. Uppenbarligen är effekten av halvvågsplattan att spegla vågens polarisationsvektor genom planet som bildas av vektorerna $\mathbf {\hat {f}}$ och $\mathbf {\hat {z}}$ . För linjärt polariserat ljus motsvarar detta att säga att effekten av halvvågsplattan är att rotera polarisationsvektorn genom en vinkel 2θ; Men för elliptiskt polariserat ljus har halvvågsplattan också effekten att invertera ljusets handenhet .

Kvartsvågsplatta

Två vågor som skiljer sig åt med en kvartsfasförskjutning för en axel.

Skapa cirkulär polarisation med hjälp av en kvartsvågsplatta och ett polariserande filter

₀ För en kvartsvågsplatta väljs förhållandet mellan L , Δ n och λ så att fasförskjutningen mellan polarisationskomponenterna är Γ = π/2. Antag nu att en linjärt polariserad våg infaller på kristallen. Denna våg kan skrivas som

(E_{f}\mathbf {\hat {f}} +E_{s}\mathbf {\hat {s }} )\mathrm {e} ^{i(kz-\omega t)},

där f- och s -axlarna är kvartsvågsplattans snabba respektive långsamma axlar, utbreder sig vågen längs z- axeln, och E _f och E _s är reella. Effekten av kvartsvågsplattan är att införa en fasförskjutningsterm e ^{i Γ} =e ^{i π/2} = i mellan vågens f- och s -komponenter, så att vågen när den lämnar kristallen nu ges av

(E_{f}\mathbf {\hat {f}} +iE_{s}\mathbf {\hat {s}} )\mathrm {e} ^{i(kz-\omega t)}.

Vågen är nu elliptiskt polariserad.

Om polarisationsaxeln för den infallande vågen väljs så att den gör en 45° med vågplattans snabba och långsamma axlar, då är E _f = E _s ≡ E , och den resulterande vågen när den lämnar vågplattan är

E(\mathbf {\hat {f}} +i\mathbf {\hat {s}} )\mathrm {e} ^{i(kz-\omega t)},

och vågen är cirkulärt polariserad.

Om polarisationsaxeln för den infallande vågen väljs så att den gör en 0° med vågplattans snabba eller långsamma axlar, kommer polarisationen inte att förändras, så den förblir linjär. Om vinkeln är mellan 0° och 45° har den resulterande vågen en elliptisk polarisation.

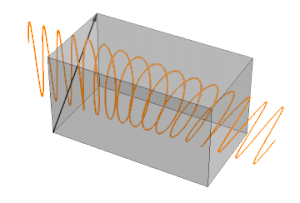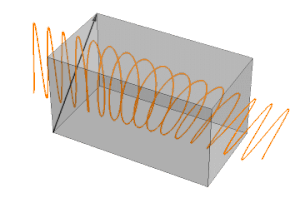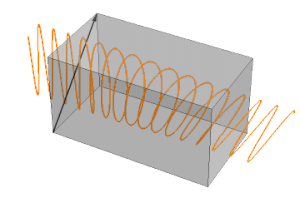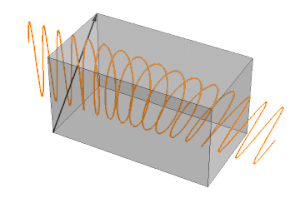
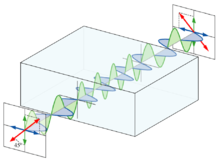
En cirkulerande polarisation kan visualiseras som summan av två linjära polarisationer med en fasskillnad på 90°. Utgången beror på ingångens polarisering. Antag att polarisationsaxlarna x och y är parallella med vågplattans långsamma och snabba axel:

Polariseringen av den inkommande fotonen (eller strålen) kan lösas som två polarisationer på x- och y-axeln. Om ingångspolarisationen är parallell med den snabba eller långsamma axeln, så finns det ingen polarisering av den andra axeln, så utpolariseringen är densamma som ingången (endast fasen mer eller mindre fördröjd). Om ingångspolarisationen är 45° mot den snabba och långsamma axeln, är polarisationen på dessa axlar lika. Men fasen för utgången av den långsamma axeln kommer att fördröjas 90° med utgången av den snabba axeln. Om inte amplituden utan båda sinusvärdena visas, kommer x och y kombinerat att beskriva en cirkel. Med andra vinklar än 0° eller 45° kommer värdena i snabb och långsam axel att skilja sig och deras resulterande utdata kommer att beskriva en ellips.

Helvågs- eller känslig nyansplatta

En helvågsplatta introducerar en fasskillnad på exakt en våglängd mellan de två polarisationsriktningarna, för en våglängd av ljus. Inom optisk mineralogi är det vanligt att använda en helvågsplatta designad för grönt ljus (en våglängd nära 540 nm). Linjärt polariserat vitt ljus som passerar genom plattan blir elliptiskt polariserat, förutom det gröna ljusets våglängd, som kommer att förbli linjär. Om en linjär polarisator orienterad vinkelrätt mot den ursprungliga polarisationen läggs till, släcks denna gröna våglängd helt men element av de andra färgerna finns kvar. Detta innebär att under dessa förhållanden kommer plattan att se en intensiv nyans av röd-violett, ibland känd som "känslig nyans". Detta ger upphov till denna plattas alternativa namn, den känsliga-tonade plattan eller (mindre vanligt) röd-toning-plattan . Dessa plattor används ofta inom mineralogi för att hjälpa till att identifiera mineraler i tunna delar av stenar .

Vågplattor av flera ordningen vs. nollordningen

En multipelordningens vågplatta är gjord av en enkel dubbelbrytande kristall som producerar en heltalsmultipel av den nominella retardansen (till exempel kan en multipelordningens halvvågsplatta ha en absolut retardans på 37λ/2). Däremot producerar en noll-ordningens vågplatta exakt den specificerade retardansen. Detta kan åstadkommas genom att kombinera två multipelordningsvågplattor så att skillnaden i deras retardanser ger den netto (verkliga) retardansen för vågplattan. Nollordningsvågplattor är mindre känsliga för temperatur- och våglängdsförskjutningar, men är dyrare än flerordningens.

Att stapla en serie vågplattor av olika ordning med polarisationsfilter mellan dem ger ett Lyot-filter . Antingen kan filtren roteras, eller så kan vågplattorna ersättas med flytande kristallskikt, för att erhålla ett brett avstämbart passband i optiskt transmissionsspektrum.

Användning av vågplattor inom mineralogi och optisk petrologi

Den känsliga nyansen (helvågs) och kvartsvågsplattorna används ofta inom området optisk mineralogi . Tillägg av plattor mellan polarisatorerna i ett petrografiskt mikroskop underlättar den optiska identifieringen av mineraler i tunna sektioner av bergarter , i synnerhet genom att tillåta deduktion av formen och orienteringen av de optiska indikationerna inom de synliga kristallsektionerna.

Rent praktiskt sätts plattan in mellan de vinkelräta polarisatorerna i en vinkel på 45 grader. Detta gör att två olika procedurer kan utföras för att undersöka mineralet under mikroskopets hårkors. För det första, i vanligt korspolariserat ljus, kan plattan användas för att särskilja orienteringen av den optiska indikatorn i förhållande till kristallförlängning – det vill säga om mineralet är "långsamt" eller "längdsnabbt" - baserat på om den synliga interferensen färgar öka eller minska med en ordning när plattan läggs till. För det andra tillåter en något mer komplicerad procedur att en nyansplatta kan användas i samband med interferensfigurtekniker för att tillåta mätning av mineralets optiska vinkel . Den optiska vinkeln (ofta betecknad som "2V") kan både vara diagnostisk för mineraltyp, såväl som i vissa fall avslöja information om variationen i kemisk sammansättning inom en enskild mineraltyp.

Se även

externa länkar

Waveplates RP photonics Encyclopedia of Laser Physics and Technology
Animation av polarisatorer och vågplattor