En 6 polytop
 6-simplex |
I 6-dimensionell geometri finns det 35 enhetliga polytoper med A 6 symmetri. Det finns en självdubbel regelbunden form, den 6-simplexa med 7 hörn.
Var och en kan visualiseras som symmetriska ortografiska projektioner i Coxeter-plan av A 6 Coxeter-gruppen och andra undergrupper.
Grafer
Symmetriska ortografiska projektioner av dessa 35 polytoper kan göras i A 6 , A 5 , A 4 , A 3 , A 2 Coxeter plan . A k grafer har [k+1] symmetri. För jämna k och symmetriska ringade diagram fördubblas symmetri till [2(k+1)] .
Dessa 35 polytoper visas var och en i dessa 5 symmetriplan, med hörn och kanter ritade, och hörn färgade av antalet överlappande hörn i varje projektiv position.
| # |
A 6 [7] |
A 5 [6] |
A 4 [5] |
A 3 [4] |
A 2 [3] |
Coxeter-Dynkin diagram Schläfli symbol Namn |
|---|---|---|---|---|---|---|
| 1 |  |
 |
 |
 |
 |
0 t {3,3,3,3,3} 6-simplex Heptapeton (hop) |
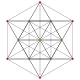
| 2 |  |
 |
 |
 |
 |
t 1 {3,3,3,3,3} Rektifierad 6-simplex Rektifierad heptapeton (ril) |
| 3 |  |
 |
 |
 |
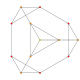 |
t 0,1 {3,3,3,3,3} Trunkerad 6-simplex Trunkerad heptapeton (til) |
| 4 |  |
 |
 |
 |
 |
t 2 {3,3,3,3,3} Birekifierad 6-simplex Birectifierad heptapeton (bril) |
| 5 |  |
 |
 |
 |
 |
t 0,2 {3,3,3,3,3} Kantellerad 6-simplex Liten rhomberad heptapeton (sril) |
| 6 |  |
 |
 |
 |
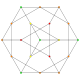 |
t 1,2 {3,3,3,3,3} Bitruncated 6-simplex Bitruncated heptapeton (batal) |
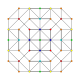
| 7 |  |
 |
 |
 |
 |
t 0,1,2 {3,3,3,3,3} Cantitruncated 6-simplex Great rhombated heptapeton (grill) |
| 8 |  |
 |
 |
 |
 |
t 0,3 {3,3,3,3,3} Runcinerad 6-simplex liten prismaterad heptapeton (spill) |
| 9 |  |
 |
 |
 |
 |
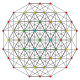
t 1,3 {3,3,3,3,3} Bikantellerad 6-simplex liten birhomberad heptapeton (sabril) |
| 10 |  |
 |
 |
 |
 |
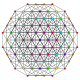
t 0,1,3 {3,3,3,3,3} Runcitruncated 6-simplex Prismatotruncated heptapeton (patal) |
| 11 |  |
 |
 |
 |
 |
t 2,3 {3,3,3,3,3} Tritruncated 6-simplex Tetradecapeton (fe) |
| 12 |  |
 |
 |
 |
 |
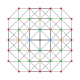
t 0,2,3 {3,3,3,3,3} Runcicantellated 6-simplex Prismatorhombated heptapeton (pril) |
| 13 |  |
 |
 |
 |
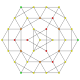 |
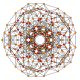
t 1,2,3 {3,3,3,3,3} Bicantitruncated 6-simplex Great birhombated heptapeton (gabril) |
| 14 |  |
 |
 |
 |
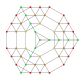 |
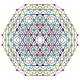
t 0,1,2,3 {3,3,3,3,3} Runcicantitrunkerad 6-simplex Stor prismatad heptapeton (gapil) |
| 15 |  |
 |
 |
 |
 |
t 0,4 {3,3,3,3,3} Stericated 6-simplex Small cellated heptapeton (scal) |
| 16 |  |
 |
 |
 |
 |
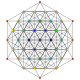
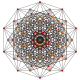
t 1,4 {3,3,3,3,3} Biruncinerad 6-simplex liten biprismato-tetradekapeton (sibpof) |
| 17 |  |
 |
 |
 |
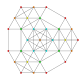 |
t 0,1,4 {3,3,3,3,3} Steritruncated 6-simplex cellitruncated heptapeton (katal) |
| 18 |  |
 |
 |
 |
 |
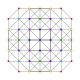
t 0,2,4 {3,3,3,3,3} sterikantellerad 6-simplex cellirhomberad heptapeton (cral) |
| 19 |  |
 |
 |
 |
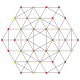 |
t 1,2,4 {3,3,3,3,3} Biruncitruncated 6-simplex Biprismatorhombated heptapeton (bapril) |
| 20 |  |
 |
 |
 |
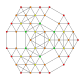 |
t 0,1,2,4 {3,3,3,3,3} Stericantitruncated 6-simplex Celligreatorhombated heptapeton (cagral) |
| 21 |  |
 |
 |
 |
 |
t 0,3,4 {3,3,3,3,3} Steriruncinerad 6-simplex celliprismaterad heptapeton (kopal) |
| 22 |  |
 |
 |
 |
 |
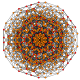
t 0,1,3,4 {3,3,3,3,3} Steriruncruncated 6-simplex celliprismatotruncated heptapeton (captal) |
| 23 |  |
 |
 |
 |
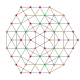 |
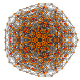
t 0,2,3,4 {3,3,3,3,3} Steriruncikantellerad 6-simplex celliprismatorhomberad heptapeton (kopril) |
| 24 |  |
 |
 |
 |
 |
t 1,2,3,4 {3,3,3,3,3} Biruncicantitruncated 6-simplex Great biprismato-tetradecapeton (gibpof) |
| 25 |  |
 |
 |
 |
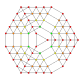 |
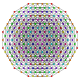
t 0,1,2,3,4 {3,3,3,3,3} Steriruncicantitruncerad 6-simplex Stor cellig heptapeton (gacal) |
| 26 |  |
 |
 |
 |
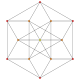 |
t 0,5 {3,3,3,3,3} Pentellerad 6-simplex liten teri-tetradecapeton (staf) |
| 27 |  |
 |
 |
 |
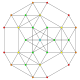 |
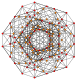
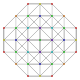
t 0,1,5 {3,3,3,3,3} Pentitruncated 6-simplex Tericellated heptapeton (tocal) |
| 28 |  |
 |
 |
 |
 |
t 0,2,5 {3,3,3,3,3} Penticantellated 6-simplex Teriprismated heptapeton (tapal) |
| 29 |  |
 |
 |
 |
 |
t 0,1,2,5 {3,3,3,3,3} Penticantitruncated 6-simplex Terigreatorhombated heptapeton (togral) |
| 30 |  |
 |
 |
 |
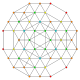 |
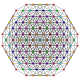
t 0,1,3,5 {3,3,3,3,3} Pentiruncitruncated 6-simplex Tericellirhombated heptapeton (tokral) |
| 31 |  |
 |
 |
 |
 |
t 0,2,3,5 {3,3,3,3,3} Pentiruncicantellated 6-simplex Teriprismatorhombi-tetradecapeton (taporf) |
| 32 |  |
 |
 |
 |
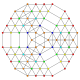 |
t 0,1,2,3,5 {3,3,3,3,3} Pentiruncicanantitruncated 6-simplex Terigreatoprismated heptapeton (tagopal) |
| 33 |  |
 |
 |
 |
 |
t 0,1,4,5 {3,3,3,3,3} Pentisteritruncated 6-simplex tericellitrunki-tetradecapeton (tactaf) |
| 34 |  |
 |
 |
 |
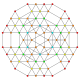 |
t 0,1,2,4,5 {3,3,3,3,3} Pentistericantitruncated 6-simplex tericelligreatorhombated heptapeton (tacogral) |
| 35 |  |
 |
 |
 |
 |
t 0,1,2,3,4,5 {3,3,3,3,3} Omnitruncated 6-simplex Great teri-tetradecapeton (gotaf) |
-
HSM Coxeter :
- HSM Coxeter, Regular Polytopes , 3:e upplagan, Dover New York, 1973
-
Kaleidoscopes: Selected Writings of HSM Coxeter , redigerad av F. Arthur Sherk, Peter McMullen, Anthony C. Thompson, Asia Ivic Weiss, Wiley-Interscience Publication, 1995, ISBN 978-0-471-01003-6
- (Papper 22) HSM Coxeter, Regular and Semi Regular Polytopes I , [Math. Zeit. 46 (1940) 380-407, MR 2,10]
- (Papper 23) HSM Coxeter, Regular and Semi-Regular Polytopes II , [Math. Zeit. 188 (1985) 559-591]
- (Papper 24) HSM Coxeter, Regular and Semi-Regular Polytopes III , [Math. Zeit. 200 (1988) 3-45]
- NW Johnson : Theory of Uniform Polytopes and Honeycombs , Ph.D. Avhandling, University of Toronto, 1966
externa länkar
- Klitzing, Richard. "6D enhetliga polytoper (polypeta)" .
Anteckningar
Kategori: