Överlappande cirklar rutnät

Exempel på överlappande runda cirkelfigurer
fyrkantiga cirkelrutnät

1+
4
9
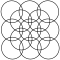
Centrerade kvadratiska gitterformer
5
13
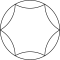
triangulära cirkelrutnät
1+
3
4
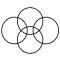
7
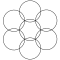
19

Ett rutnät med överlappande cirklar är ett geometriskt mönster av upprepande , överlappande cirklar med samma radie i tvådimensionellt utrymme . Vanligtvis är mönster baserade på cirklar centrerade på trianglar (med den enkla formen med två cirklar som heter vesica piscis ) eller på det kvadratiska gittermönstret av punkter.

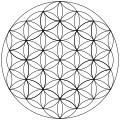
Mönster av sju överlappande cirklar förekommer i historiska artefakter från 700-talet f.Kr. och framåt; de blir en ofta använd prydnad under det romerska imperiet och överlever in i medeltida konstnärliga traditioner både inom islamisk konst ( girih -dekorationer) och i gotisk konst . Namnet "Livets blomma" ges till mönstret med överlappande cirklar i New Age- publikationer.

Av särskilt intresse är rosetten med sex kronblad som härrör från mönstret "sju överlappande cirklar", även känd som " Alpernas sol " från dess frekventa användning i alpin folkkonst på 1600- och 1700-talet.

Triangulärt rutnät av överlappande cirklar


Det här mönstret kan förlängas i det oändliga, ses här med hexagonala ringar med 1, 7, 19, 37, 61, 91 cirklar...

Den triangulära gitterformen, med cirkelradier lika med deras separation kallas ett rutnät med sju överlappande cirklar . Den innehåller 6 cirklar som skär varandra i en punkt, med en 7:e cirkel centrerad på den skärningspunkten.

Överlappande cirklar med liknande geometriska konstruktioner har använts sällan inom olika dekorativa konster sedan antiken. Mönstret har hittat ett brett användningsområde inom populärkulturen, inom mode , smycken , tatueringar och dekorativa produkter.

Kulturell betydelse

Nära öst

Den äldsta kända förekomsten av mönstret med "överlappande cirklar" dateras till 700- eller 600-talet f.Kr., på tröskeln till den assyriske kungen Aššur-bāni-aplis palats i Dur Šarrukin (nu i Louvren ).

Designen blir mer utbredd under de tidiga århundradena av den gemensamma epoken. Ett tidigt exempel är fem mönster av 19 överlappande cirklar ritade på granitpelare vid Temple of Osiris i Abydos , Egypten , och ytterligare fem på kolumn mittemot byggnaden. De är ritade i röd ockra och en del är mycket svaga och svåra att urskilja. Mönstren är graffiti och finns inte i inhemska egyptiska ornament. De är mestadels daterade till de tidiga århundradena av den kristna eran även om medeltida eller till och med modernt (tidigt 1900-tal) ursprung inte kan uteslutas med säkerhet, eftersom teckningarna inte nämns i de omfattande listorna över graffiti vid templet som sammanställts av Margaret Murray i 1904.

Liknande mönster användes ibland i England som apotropaiska märken för att hindra häxor från att komma in i byggnader. Vigningskors som indikerar punkter i kyrkor som smords med heligt vatten under en kyrkoinvigning tar också formen av överlappande cirklar.

Ett girih -mönster som kan ritas med kompass och rak kant

Fönsterbur vid Topkapi-palatset , med mönster

I islamisk konst är mönstret ett av flera arrangemang av cirklar (andra som används för fyrfaldiga eller femfaldiga mönster) som används för att konstruera rutnät för islamiska geometriska mönster . Den används för att designa mönster med 6- och 12-uddiga stjärnor samt hexagoner i stilen som kallas girih . De resulterande mönstren döljer dock karaktäristiskt konstruktionsnätet, och presenterar istället en design av sammanflätade bandverk .

Europa

Mönster av sju överlappande cirklar finns på en cypro-arkaisk I-kopp från 700-talet f.Kr. på Cypern [ ^{citat behövs ]} och romerska mosaiker, till exempel i Herodes palats under 1000-talet f.Kr.

Designen finns på en av silverplattorna från den senromerska skatten Kaiseraugst (upptäckt 1961). Den återfinns senare som en prydnad i gotisk arkitektur och ännu senare i europeisk folkkonst från den tidigmoderna perioden.

Högmedeltida exempel inkluderar Cosmati- trottoarerna i Westminster Abbey (1200-talet). Leonardo da Vinci diskuterade uttryckligen designens matematiska proportioner.

Modernt bruk

19-cirkel med bågar Hänge , silver, ⌀ 27 mm (kommersiell produkt, 2013)

Namnet "Livets blomma" är modernt, förknippat med New Age -rörelsen och tillskrivs vanligtvis Drunvalo Melchizedek i hans bok The Ancient Secret of the Flower of Life (1999).

Mönstret och det moderna namnet har spridit sig till ett brett användningsområde inom populärkulturen, inom mode, smycken, tatueringar och dekorativa produkter. Mönstret i quiltning har kallats diamantvigselring eller triangelvigselring för att kontrastera det från det kvadratiska mönstret . Förutom en tillfällig användning inom mode, används den också inom dekorativ konst. använder albumet Sempiternal (2013) av Bring Me the Horizon rutnätet med 61 överlappande cirklar som huvuddraget på skivomslaget, medan albumet A Head Full of Dreams (2015) av Coldplay har rutnätet med 19 överlappande cirklar som centrala delen av skivomslaget. Teaseraffischer som illustrerar omslagsbilden till A Head Full of Dreams visades flitigt på Londons tunnelbana den sista veckan i oktober 2015.

"Alpernas sol" ( italienska Sole delle Alpi ) har använts som emblem för padansk nationalism i norra Italien sedan 1990-talet. Det liknar ett mönster som ofta finns i det området på byggnader.

Galleri

1, 7 och 19-cirklar hexagonal variant

I exemplen nedan har mönstret en hexagonal kontur och är ytterligare avgränsat.

Leonardo da Vincis teckning från Codex Atlanticus , mellan 1478 och 1519.
Teckning av Leonardo da Vinci ( Codex Atlanticus , fol. 307v)
1-cirkel med färdiga bågar
7-cirkel: Mosaikgolv från ett badhus i Herodes palats , 1:a århundradet f.Kr.
19-cirkelsymbol med färdiga bågar och avgränsad av en större cirkel
19-cirkel: Två symboler ritade i Osiris-templet i Abydos, Egypten
19-cirkel: Ett fönster vid den södra apsisen av kyrkan Preveli-klostret (Moni Preveli), Kreta.
19-cirkel: Från Efesos , Turkiet

Liknande mönster

I exemplen nedan har mönstret ingen hexagonal kontur.

Bägare med mytologiska scener, en sfinxfris och representationen av en kung som besegrar sina fiender. Cypro-arkaiska I (8:e–7:e århundradena f.Kr.). Från Idalion, Cypern .
Boll som hålls av det manliga kejserliga väktarlejonet vid porten till Supreme Harmony , Förbjudna staden , Peking , Kina, som visar det geometriska mönstret på dess yta.
Golvdekoration från kung Ashurbanipals palats i norra Irak , synlig i Louvren, daterad 645 f.Kr.
Kaffekopp (Tyskland, 2022)
" Sun of the Alps " emblem som används av Lega Nord

Konstruktion

Martha Bartfeld, författare till handledningsböcker för geometrisk konst, beskrev sin självständiga upptäckt av designen 1968. Hennes ursprungliga definition sa: "Denna design består av cirklar med en radie på 1-[tum; 25 mm], där varje skärningspunkt fungerar som ett nytt centrum. Designen kan utökas i oändlighet beroende på hur många gånger de udda punkterna är markerade."

Mönsterfiguren kan ritas med penna och kompass genom att skapa flera serier av sammanlänkade cirklar med samma diameter som rör vid föregående cirkels centrum. Den andra cirkeln är centrerad vid vilken punkt som helst på den första cirkeln. Alla följande cirklar är centrerade på skärningspunkten mellan två andra cirklar.

Framsteg

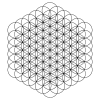
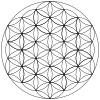
Mönstret kan förlängas utåt i koncentriska hexagonala ringar av cirklar, som visas. Den första raden visar ringar av cirklar. Den andra raden visar en tredimensionell tolkning av en uppsättning av n × n × n kub av sfärer sett från en diagonal axel. Den tredje raden visar mönstret färdigt med partiella cirkelbågar inom en uppsättning färdiga cirklar.

Expanderande uppsättningar har 1, 7, 19, 37, 61, 91, 127, etc. cirklar, och fortlöpande allt större hexagonala ringar av cirklar. Antalet cirklar är n ³ -( n -1) ³ = 3 n ² -3 n +1 = 3 n ( n -1)+1.

Dessa överlappande cirklar kan också ses som en projektion av en n -enhetskub av sfärer i 3-dimensionell rymd, sett på den diagonala axeln. Det finns fler sfärer än cirklar eftersom vissa överlappar i två dimensioner.

Rosettfigurer inklusive delcirklar
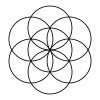
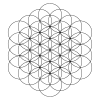
1-cirkel	7-cirklar (8-1)	19-cirkel (27-8)	37-cirkel (64-27)	61-cirkel (125-64)	91-cirkel (216-125)	127-cirkel... (343-216)

1-sfär (1×1×1)	8-sfär (2×2×2)	27-sfär (3×3×3)	64-sfär (4×4×4)	125-sfär (5×5×5)	216-sfär (6×6×6)	343-sfär (7×7×7)

+12 bågar	+24 bågar	+36 bågar	+48 bågar	+60 bågar	+72 bågar	+84 bågar

Andra varianter

En annan triangulär gitterform är vanlig, med cirkelseparation som kvadratroten av 3 gånger deras radie. Richard Kershner visade 1939 att inget arrangemang av cirklar kan täcka planet mer effektivt än detta hexagonala gitterarrangemang.

Två offsetkopior av detta cirkelmönster ger ett rombiskt kakelmönster , medan tre kopior gör det ursprungliga triangulära mönstret.

19 cirkel exempel
Två offsetkopior av det minimala täckande cirkelmönstret (vänster) gör ett rombiskt kakelmönster , som denna röda, blå version.
Tre offsetkopior av det minimala täckande cirkelmönstret (bilden längst till vänster) gör det 7-cirkelmönster, som denna röda, gröna, blå version.
Exempel på Ayyubid Raqqa glaserad burk i stengods. Syrien, 1100-/1200-talet
Svartvit mosaikbeläggning vid Hadrianus villa , Tivoli, 200-talet e.Kr

Relaterade begrepp

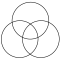
Mittlinsen av 2 - cirkelfiguren kallas en vesica piscis , från Euclid . Två cirklar kallas också Villarceau-cirklar som en plan skärningspunkt mellan en torus. Områdena innanför en cirkel och utanför den andra cirkeln kallas en lune .

Den 3-cirklara figuren liknar en skildring av borromeiska ringar och används i 3-set teori Venn diagram . Dess inre gör en unikursal väg som kallas en triquetra . Mitten av 3-cirkelfiguren kallas en reuleaux triangel .

Vesica piscis	Borromeanska ringar	Venn diagram	Triquetra	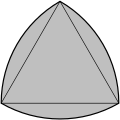Reuleaux triangel

Vissa sfäriska polyedrar med kanter längs stora cirklar kan stereografiskt projiceras på planet som överlappande cirklar.

Polyeder i stereografisk projektion
oktaeder	Cuboctahedron	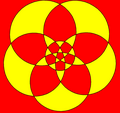Icosidodecahedron

Mönstret med 7 cirklar har också kallats ett islamiskt mönster med sju cirklar för dess användning i islamisk konst .

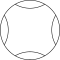
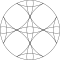
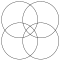
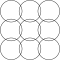
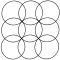
Fyrkantigt rutnät av överlappande cirklar

Fyrkantig gallerform
Cirkelradien är kvadratroten av 2 gånger deras separation.	En quiltdesign som kallas ett dubbelt vigselringmönster.

Centrerad kvadratisk gallerform
Det kan ses som två halvförskjutna kvadratiska rutnät av tangentcirklar.	Egyptisk design, från Owen Jones's The Grammar of Ornament (1856)

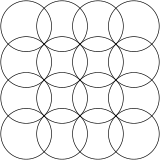
Den kvadratiska gitterformen kan ses med cirklar som är i linje horisontellt och vertikalt, samtidigt som de skär varandra på sina diagonaler. Mönstret ser något annorlunda ut när det roteras på sin diagonal, även kallat en centrerad kvadratisk gitterform eftersom det kan ses som två kvadratiska gitter med var och en centrerad på den andras mellanrum.

Det kallas ett Kawung-motiv i indonesisk batik och finns på väggarna i det hinduiska templet Prambanan från 800-talet på Java .

Det kallas en Apsamikkum från forntida mesopotamisk matematik.

Det fyrkantiga rutnätet kan ses i ett ansiktscentrerat kubiskt gitter , med 12 sfärer i kontakt runt varje sfär
Det relaterade rutnätet med fem överlappande cirklar är konstruerat av två uppsättningar av överlappande cirklar halvförskjutning.
Kawung eller "Coffee Bean" Batik sarong (detalj), Java, Indonesien

Se även

Uniform bricksymmetrimutationer - mönstermutationer i 3D-rymden
Knutteori

externa länkar

Weisstein, Eric W. "Circle-circle intersection" . MathWorld .
Livets blomma artikel från The Mystica