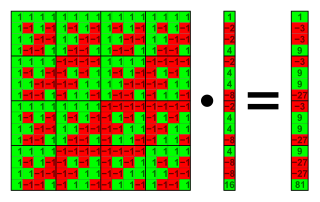
Walsh matris

Walshmatris av ordningen 16 multiplicerad med en vektor

Naturligt ordnad Hadamard-matris permuterad till sekvensordnad Hadamard-matris. Antalet teckenändringar per rad i den naturligt ordnade matrisen är (0, 15, 7, 8, 3, 12, 4, 11, 1, 14, 6, 9, 2, 13, 5, 10), i sekvensen -ordnad matris antalet teckenändringar är i följd.

LDU-nedbrytning av en Walsh-matris. De i de triangulära matriserna bildar Sierpinski-trianglar . Posterna i den diagonala matrisen är värden från Goulds sekvens , med minustecknen fördelade som de i Thue–Morse-sekvensen .

Binär Walsh-matris som en matrisprodukt . Den binära matrisen (vit 0, röd 1) är resultatet med operationer i F ₂ . De grå siffrorna visar resultatet med operationer i R .

Se även: Hadamard-matris

Inom matematik är en Walsh-matris en specifik kvadratisk matris med dimensionerna 2 ⁿ , där n är ett visst naturligt tal. Matrisens poster är antingen +1 eller −1 och dess rader såväl som kolumner är ortogonala, dvs punktprodukten är noll. Walsh-matrisen föreslogs av Joseph L. Walsh 1923. Varje rad i en Walsh-matris motsvarar en Walsh-funktion .

Walsh-matriserna är ett specialfall av Hadamard-matriser . Den naturligt ordnade Hadamard-matrisen definieras av den rekursiva formeln nedan, och den sekvensordnade Hadamard-matrisen bildas genom att omarrangera raderna så att antalet teckenändringar i en rad är i ökande ordning. Förvirrande nog hänvisar olika källor till endera matrisen som Walsh-matrisen.

Walsh-matrisen (och Walsh-funktionerna ) används vid beräkning av Walsh-transformen och har tillämpningar för effektiv implementering av vissa signalbehandlingsoperationer.

Formel

Hadamard-matriserna med dimension 2 ^k för k ∈ N ges av den rekursiva formeln (den lägsta ordningen för Hadamard-matrisen är 2):

${\ start{aligned}H\left(2^{1}\right)&={\begin{bmatrix}1&1\\1&-1\end{bmatrix}},\\H\left(2^{2}\right )&={\begin{bmatrix}1&1&1&1\\1&-1&1&-1\\1&1&-1&-1\\1&-1&-1&1\\\end{bmatrix}},\end{aligned}}$

och i allmänhet

$H\left(2^{k}\right)={\begin{bmatrix}H\left(2^{k-1}\right)&H\left(2^{k-1}\right )\\H\left(2^{k-1}\right)&-H\left(2^{k-1}\right)\end{bmatrix}}=H(2)\ibland H\left( 2^{k-1}\höger),$

för 2 ≤ k ∈ N , där ⊗ anger Kronecker - produkten .

Permutation

Ordna om raderna i matrisen efter antalet teckenförändringar för varje rad. Till exempel i

$\displaystyle H(4)={\begin{bmatrix}1&1&1&1\\1&-1&1&- 1\\1&1&-1&-1\\1&-1&-1&1\\\end{bmatrix}}}$

de på varandra följande raderna har 0, 3, 1 och 2 teckenändringar. Om vi ​​ordnar om raderna i sekvensordning:

$4)={\begin{bmatrix}1&1&1&1\\1&1&-1& -1\\1&-1&-1&1\\1&-1&1&-1\\\end{bmatrix}},}$

sedan har de på varandra följande raderna 0, 1, 2 och 3 teckenändringar.

Alternativa former av Walsh-matrisen

Sekvensordning

Sekvensordningen för raderna i Walsh-matrisen kan härledas från ordningen av Hadamard-matrisen genom att först applicera bitomvändningspermutationen och sedan gråkodspermutationen :

$W(8)={\begin{bmatrix}1&1&1&1&1&1&1&1\\1&1&1&1&-1&-1&-1&-1\\1&1&-1&-1&-1&-1&1&1\\\1&1&-1&-1&1&1&-1&-1\\\ 1&-1&-1&1&1&-1&-1&1\\1&-1&-1&1&-1&1&1&-1\\1&-1&1&-1&-1&1&-1&1\\\1&-1&1&-1&1&-1&1&-1\\\end{bmatrix}} ,$

där de på varandra följande raderna har 0, 1, 2, 3, 4, 5, 6 och 7 teckenändringar.

Dyadisk ordning

$W(8)={\begin{bmatrix}1&1&1&1&1&1&1&1\\1&1&1&1&-1&-1&-1&-1\\1&1&-1&-1&1&1&-1&-1\\\1&1&-1&-1&-1&-1&1&1\\\ 1&-1&1&-1&1&-1&1&-1\\1&-1&1&-1&-1&1&-1&1\\1&-1&-1&1&1&-1&-1&1\\1&-1&-1&1&-1&1&1&-1\\\end{bmatrix}} ,$

där de på varandra följande raderna har 0, 1, 3, 2, 7, 6, 4 och 5 teckenändringar.

Naturlig ordning

$W(8)={\begin{bmatrix}1&1&1&1&1&1&1&1\\1&-1&1&-1&1&-1&1&-1\\1&1&-1&-1&1&1&-1&-1\\\1&-1&-1&1&1&-1&-1&1\\\ 1&1&1&1&-1&-1&-1&-1\\1&-1&1&-1&-1&1&-1&1\\1&1&1&-1&-1&-1&-1&1&1\\\1&-1&-1&1&-1&1&1&-1\\\end{bmatrix}} ,$

där de på varandra följande raderna har 0, 7, 3, 4, 1, 6, 2 och 5 teckenändringar.

Se även

• Haar wavelet
• Quincunx matris
• Hadamard transformation
• Code-division multiple access
• OEIS : A228539 ( OEIS : A228540 ) – rader av de (negerade) binära Walsh-matriserna läses som omvända binära tal
• OEIS : A197818 – antidiagonaler för den negerade binära Walsh-matrisen läses som binära tal