Trafikflöde

Inom matematik och transportteknik är trafikflöde studiet av interaktioner mellan resenärer (inklusive fotgängare, cyklister, förare och deras fordon) och infrastruktur (inklusive motorvägar, skyltar och trafikkontrollanordningar), i syfte att förstå och utveckla en optimal transportnät med effektiv förflyttning av trafik och minimala problem med trafikstockningar .

Historia

Försök att producera en matematisk teori om trafikflöde går tillbaka till 1920-talet, när Frank Knight först gjorde en analys av trafikjämvikt, som förfinades till Wardrops första och andra jämviktsprincip 1952.

Icke desto mindre, även med tillkomsten av betydande datorprocessorkraft, har det hittills inte funnits någon tillfredsställande allmän teori som konsekvent kan tillämpas på verkliga flödesförhållanden. Nuvarande trafikmodeller använder en blandning av empiriska och teoretiska tekniker. Dessa modeller utvecklas sedan till trafikprognoser och tar hänsyn till föreslagna lokala eller större förändringar, såsom ökad fordonsanvändning, förändringar i markanvändning eller förändringar i transportsätt (med människor som flyttar från buss till tåg eller bil, till exempel). och att identifiera områden med överbelastning där nätet behöver justeras.

Översikt

Passagerarkapacitet för olika transportsätt

Vägutrymmeskrav

Trafiken beter sig på ett komplext och olinjärt sätt, beroende på interaktionen mellan ett stort antal fordon . På grund av mänskliga förares individuella reaktioner interagerar fordon inte bara efter mekanikens lagar, utan visar snarare klusterbildning och stötvågsutbredning , [ ^{citat behövs ]} både framåt och bakåt, beroende på fordonets täthet . Vissa matematiska modeller av trafikflöde använder ett vertikalt köantagande, där fordonen längs en överbelastad länk inte spiller tillbaka längs länkens längd.

I ett fritt flytande nätverk hänvisar trafikflödesteori till trafikströmsvariablerna hastighet, flöde och koncentration. Dessa relationer handlar främst om oavbrutet trafikflöde, främst på motorvägar eller motorvägar. Flödesförhållanden anses vara "fria" när mindre än 12 fordon per mil per körfält är på en väg. "Stall" beskrivs ibland som 12–30 fordon per mil per fil. När tätheten når den maximala massflödeshastigheten (eller flödet ) och överstiger den optimala densiteten (över 30 fordon per mil per körfält), blir trafikflödet instabilt, och även en mindre incident kan resultera i ihållande körförhållanden för stopp och kör . Ett "haveri"-tillstånd uppstår när trafiken blir instabil och överstiger 67 fordon per mil per fil. "Kyltäthet" avser extrem trafiktäthet när trafikflödet stannar helt, vanligtvis i intervallet 185–250 fordon per mil per fil.

Men beräkningar av överbelastade nät är mer komplexa och bygger mer på empiriska studier och extrapolationer från faktiska vägräkningar. Eftersom dessa ofta är urbana eller förortsmässiga, påverkar även andra faktorer (såsom trafikanters säkerhet och miljöhänsyn) de optimala förhållandena.

Trafikströmsegenskaper

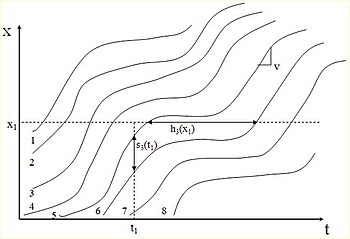
Trafikflödet är i allmänhet begränsat längs en endimensionell väg (t.ex. ett körfält). Ett tid-rymddiagram visar grafiskt flödet av fordon längs en väg över tiden. Tiden visas längs den horisontella axeln och avståndet visas längs den vertikala axeln. Trafikflödet i ett tid-rumsdiagram representeras av de individuella banlinjerna för enskilda fordon. Fordon som följer efter varandra längs ett givet körfält kommer att ha parallella banor, och banor kommer att korsas när ett fordon passerar ett annat. Tid-rumsdiagram är användbara verktyg för att visa och analysera trafikflödesegenskaperna för ett givet vägsegment över tid (t.ex. analysera trafikstockningar).

Det finns tre huvudvariabler för att visualisera en trafikström: hastighet (v), täthet (angivet k; antalet fordon per utrymmesenhet) och flöde [ ^{förtydligande behövs ]} (anges q; antalet fordon per tidsenhet) .

Figur 1. Time Space diagram

Fart

Hastighet är avståndet per tidsenhet. Man kan inte spåra hastigheten på varje fordon; så i praktiken mäts medelhastigheten genom att provtagning av fordon i ett givet område över en tidsperiod. Två definitioner av medelhastighet identifieras: "tidmedelhastighet" och "rymdmedelhastighet".

"Tidsmedelhastighet" mäts vid en referenspunkt på vägbanan under en tidsperiod. I praktiken mäts det genom användning av loopdetektorer. Slingdetektorer kan, när de är spridda över ett referensområde, identifiera varje fordon och spåra dess hastighet. Medelhastighetsmätningar som erhålls från denna metod är emellertid inte korrekta eftersom momentana hastigheter som medelvärdesmätningar över flera fordon inte tar hänsyn till skillnaden i restid för de fordon som färdas med olika hastigheter över samma sträcka. ^{[ förtydligande behövs ]}
$v_{t}=(1/m)\summa _{i=1}^{m}v_{i}$

där m representerar antalet fordon som passerar den fasta punkten och v _i är hastigheten för det i: te fordonet.
"Rymdens medelhastighet" mäts över hela vägsegmentet. På varandra följande bilder eller video av ett vägsegment spårar hastigheten för enskilda fordon, och sedan beräknas medelhastigheten. Den anses vara mer exakt än tidens medelhastighet. Data för rymdberäkning av rymdmedelhastighet kan hämtas från satellitbilder, en kamera eller båda. $v_{s}=\left((1/n)\summa _{i=1}^{n }(1/v_{i})\right)^{-1}$
där n representerar antalet fordon som passerar vägsegmentet.

"Rymden medelhastighet" är alltså det harmoniska medelvärdet av hastigheterna. Tidens medelhastighet är aldrig mindre än medelhastigheten för rymden: $v_{t}=v_{s}+{\frac {\sigma _{s}^{2} }{v_{s}}}$ , där $\sigma _{s}^{2}$ är variansen av rymdmedelhastigheten

Figur 2. Rymdmedel- och tidsmedelhastigheter

I ett tid-rymddiagram är den momentana hastigheten, v = dx/dt, för ett fordon lika med lutningen längs fordonets bana. Medelhastigheten för ett fordon är lika med lutningen på linjen som förbinder banslutpunkterna där ett fordon går in i och lämnar vägsegmentet. Den vertikala avståndet (avståndet) mellan parallella banor är fordonsavståndet (s) mellan ett ledande och efterföljande fordon. På liknande sätt representerar den horisontella separationen (tiden) fordonets framsteg (h). Ett tid-rum-diagram är användbart för att relatera framsteg och avstånd till trafikflöde respektive täthet.

Densitet

Densitet (k) definieras som antalet fordon per längdenhet av vägbanan. I trafikflödet är de två viktigaste tätheterna den kritiska densiteten ( k _c ) och jamdensiteten ( k _j ). Den maximala densiteten som kan uppnås under fritt flöde är _kc , medan kj är den maximala densiteten som uppnås under trängsel _. I allmänhet är syltdensiteten fem gånger den kritiska densiteten. Omvänd densitet är avståndet (s), vilket är mitt-till-centrum-avståndet mellan två fordon.

$k={\frac {1}{s}}$

Figur 3. Flödesdensitetssamband

Figur 4. Samband mellan flöde ( q ), densitet ( k ) och hastighet ( v )

Densiteten ( k ) inom en vägbana ( L ) vid en given tidpunkt ( _t1 ) är lika med inversen av medelavståndet för de n fordonen.

$K(L,t_{1})={\frac {n}{L}}={\frac {1}{{ \bar {s}}(t_{1})}}$

I ett tidsrymddiagram kan tätheten utvärderas i region A.

$k(A)={\frac {n}{L}}={\frac {n\,dt}{L\,dt}}={\frac {tt}{\left|A\right\ vert }}$

där tt är den totala restiden i A .

Figur 5

Flöde

Flöde ( q ) är antalet fordon som passerar en referenspunkt per tidsenhet, fordon per timme. Det omvända till flödet är framfart ( h ), vilket är tiden som går mellan det i :te fordonet som passerar en referenspunkt i rymden och ( i + 1):e fordonet. Vid trängsel h konstant. När en trafikstockning bildas h oändligheten.

$q=kv\,$

$q=1/h\,$

Flödet ( q ) som passerar en fast punkt ( x ₁ ) under ett intervall ( T ) är lika med inversen av medelhastigheten för de m fordonen.

$q(T,x_{1})={\frac {m}{T}}={\frac {1}{{ \bar {h}}(x_{1})}}$

kan flödet utvärderas i regionen B.

$q(B)={\frac {m}{T}}={\frac {m\,dx}{T\,dx}}={\frac {td}{\left|B\right\ vert }}$

där td är den totala tillryggalagda sträckan i B .

Bild 6

Analysmetoder

Analytiker närmar sig problemet på tre huvudsakliga sätt, motsvarande de tre huvudsakliga observationsskalorna i fysik:

Mikroskopisk skala : På den mest grundläggande nivån betraktas varje fordon som en individ. En ekvation kan skrivas för varje, vanligtvis en vanlig differentialekvation (ODE). Cellulära automationsmodeller kan också användas, där vägen är indelad i celler, som var och en innehåller en rörlig bil, eller är tom. Nagel –Schreckenberg-modellen är ett enkelt exempel på en sådan modell. När bilarna interagerar kan den modellera kollektiva fenomen som trafikstockningar .
Makroskopisk skala : I likhet med modeller av vätskedynamik anses det vara användbart att använda ett system av partiella differentialekvationer , som balanserar lagar för vissa bruttokvantiteter av intresse; t.ex. fordonens densitet eller deras medelhastighet.
Mesoskopisk (kinetisk) skala: En tredje, mellanliggande möjlighet, är att definiera en funktion $f(t,x,V)$ som uttrycker sannolikheten att ha ett fordon vid tidpunkten ${\ displaystyle t}$ i position $x$ som körs med hastigheten $V$ . Denna funktion, efter metoder för statistisk mekanik , kan beräknas med hjälp av en integro-differentialekvation som Boltzmann-ekvationen .

Det tekniska tillvägagångssättet för analys av problem med motorvägstrafik är i första hand baserad på empirisk analys (dvs observation och matematisk kurvanpassning). En viktig referens som används av amerikanska planerare är Highway Capacity Manual , publicerad av Transportation Research Board , som är en del av United States National Academy of Sciences . Detta rekommenderar att man modellerar trafikflöden med hjälp av hela restiden över en länk med hjälp av en fördröjnings-/flödesfunktion, inklusive effekterna av köbildning. Denna teknik används i många amerikanska trafikmodeller och i SATURN-modellen i Europa.

I många delar av Europa används en hybrid empirisk strategi för trafikdesign, som kombinerar makro-, mikro- och mesoskopiska egenskaper. Istället för att simulera ett stadigt tillstånd av flöde för en resa, simuleras övergående "efterfrågetoppar" av trängsel. Dessa modelleras genom att använda små "tidsskivor" över nätverket under hela arbetsdagen eller helgen. Vanligtvis uppskattas först ursprung och destinationer för resor och en trafikmodell genereras innan den kalibreras genom att jämföra den matematiska modellen med observerade räkningar av faktiska trafikflöden, klassificerade efter fordonstyp. "Matrisuppskattning" appliceras sedan på modellen för att uppnå en bättre matchning med observerade länkräkningar före eventuella förändringar, och den reviderade modellen används för att generera en mer realistisk trafikprognos för varje föreslaget schema. Modellen skulle köras flera gånger (inklusive en aktuell baslinje, en "genomsnittlig dag"-prognos baserad på en rad ekonomiska parametrar och stödd av känslighetsanalys) för att förstå implikationerna av tillfälliga blockeringar eller incidenter runt nätverket. Från modellerna är det möjligt att summera den tid det tar för alla förare av olika typer av fordon på nätet och därmed härleda genomsnittlig bränsleförbrukning och utsläpp.

Mycket av brittiska, skandinaviska och holländska myndigheters praxis är att använda modelleringsprogrammet CONTRAM för stora projekt, som har utvecklats under flera decennier under överinseende av Storbritanniens Transport Research Laboratory, och på senare tid med stöd av Svenska Vägverket . Genom att modellera prognoser för vägnätet för flera decennier in i framtiden kan de ekonomiska fördelarna av förändringar av vägnätet beräknas med hjälp av uppskattningar av tidsvärde och andra parametrar. Resultatet av dessa modeller kan sedan matas in i ett kostnads-nyttoanalysprogram.

Kumulativa fordonsräkningskurvor ( N -kurvor)

En kumulativ fordonsräkningskurva, N -kurvan, visar det kumulativa antalet fordon som passerar en viss plats x med tiden t , mätt från passagen av något referensfordon. Denna kurva kan plottas om ankomsttiderna är kända för enskilda fordon som närmar sig en plats x , och avgångstiderna är också kända när de lämnar plats x . Att erhålla dessa ankomst- och avgångstider kan involvera datainsamling: till exempel kan man ställa in två punktsensorer på platserna X ₁ och X ₂ och räkna antalet fordon som passerar detta segment samtidigt som man registrerar tiden för varje fordon anländer till X ₁ och avgår från X ₂ . Den resulterande kurvan är ett par kumulativa kurvor där den vertikala axeln ( N ) representerar det kumulativa antalet fordon som passerar de två punkterna: X ₁ och X ₂ , och den horisontella axeln ( t ) representerar den förflutna tiden från X ₁ och X ₂ .

Figur 8. Enkla kumulativa kurvor

Figur 9. Kurvor för ankomst, virtuell ankomst och avgång

Om fordon inte upplever någon fördröjning när de färdas från X ₁ till X ₂ representeras ankomsterna av fordon på plats X _{1 av kurvan} N ₁ och ankomsterna av fordonen på plats X ₂ representeras av N ₂ i figur 8. Mer vanligen är kurvan _N1 känd som ankomstkurvan för fordon vid position X1 och kurvan _N2 är känd som _{ankomstkurvan} för fordon vid position X2 _. Använd en enfilig signaliserad inflygning till en korsning som ett exempel, där X ₁ är platsen för stopplisten vid inflygningen och X ₂ är en godtycklig linje på mottagningsfilen tvärs över korsningen, när trafiksignalen är grön , kan fordon färdas genom båda punkterna utan fördröjning och tiden det tar att färdas det avståndet är lika med restiden med fritt flöde. Grafiskt visas detta som de två separata kurvorna i figur 8.

Men när trafiksignalen är röd kommer fordon fram till stopplisten ( X ₁ ) och försenas av rött ljus innan de korsar X ₂ en tid efter att signalen blivit grön. Som ett resultat byggs det upp en kö vid stoppbaren när fler fordon anländer till korsningen medan trafiksignalen fortfarande är röd. Så länge fordon som anländer till korsningen fortfarande hindras av kön, representerar därför kurvan _N2_inte längre fordonens ankomst till plats X2 ; den _{representerar} nu fordonens virtuella ankomst till plats X2 , eller med andra ord, den representerar fordonens ankomst till X2 om _de inte upplevde någon försening. Fordonens ankomst till plats X ₂ , med hänsyn tagen till fördröjningen från trafiksignalen, representeras nu av kurvan N′ ₂ i figur 9.

Konceptet med den virtuella ankomstkurvan är dock felaktigt. Denna kurva visar inte korrekt kölängden till följd av trafikavbrottet (dvs röd signal). Den förutsätter att alla fordon fortfarande når stopplisten innan de försenas av rött ljus. Med andra ord visar den virtuella ankomstkurvan staplingen av fordon vertikalt vid stopplisten. När trafiksignalen blir grön serveras dessa fordon i en först-in-först-ut-ordning (FIFO). För ett flerfiligt tillvägagångssätt är serviceordern emellertid inte nödvändigtvis FIFO. Ändå är tolkningen fortfarande användbar på grund av oron med genomsnittlig total försening istället för totala förseningar för enskilda fordon.

Stegfunktion kontra smidig funktion

Figur 10. Stegfunktion

Trafikljusexemplet visar N -kurvor som mjuka funktioner. Teoretiskt sett bör dock plottning av N -kurvor från insamlad data resultera i en stegfunktion (figur 10). Varje steg representerar ankomsten eller avgången för ett fordon vid den tidpunkten. När N -kurvan ritas i större skala som speglar en tidsperiod som täcker flera cykler, kan stegen för enskilda fordon ignoreras, och kurvan kommer då att se ut som en jämn funktion (figur 8).

Trafikuppdrag

Figur 14. Fyrstegsmodellen för färdbehov för trafiktilldelning

Syftet med trafikflödesanalys är att skapa och implementera en modell som gör det möjligt för fordon att nå sin destination på kortast möjliga tid med maximal vägkapacitet. Detta är en process i fyra steg:

Generation – programmet uppskattar hur många resor som skulle genereras. För detta behöver programmet statistiska uppgifter om bostadsområden efter befolkning, plats för arbetsplatser etc.;
Distribution – efter generering skapar den de olika ursprung-destinationsparen (OD) mellan platsen som hittades i steg 1;
Modal Split/Mode Choice – systemet måste bestämma hur stor andel av befolkningen som skulle delas mellan olika tillgängliga transportsätt, t.ex. bilar, bussar, järnvägar, etc.;
Rutttilldelning – slutligen tilldelas rutter till fordonen baserat på regler för minimikriterier.

Denna cykel upprepas tills lösningen konvergerar.

Det finns två huvudsakliga tillvägagångssätt för att tackla detta problem med slutmålen:

System optimalt

Kort sagt, ett nätverk är i systemoptimum (SO) när den totala systemkostnaden är den lägsta av alla möjliga uppdrag.

System Optimum bygger på antagandet att rutter för alla fordon skulle styras av systemet, och att omdirigering skulle baseras på maximalt utnyttjande av resurser och minsta totala systemkostnad. (Kostnad kan tolkas som restid.) I en System Optimum routingalgoritm har därför alla rutter mellan ett givet OD-par samma marginalkostnad. I traditionell transportekonomi bestäms System Optimum av jämvikten mellan efterfrågefunktion och marginalkostnadsfunktion. I detta tillvägagångssätt skildras marginalkostnaden grovt som en ökande funktion i trafikstockningar. I trafikflödesansats kan marginalkostnaden för resan uttryckas som summan av kostnaden (fördröjningstid, w ) som föraren upplever och den externa ( e ) som en förare ålägger resten av användarna.

₀₀₀₀ Anta att det finns en motorväg (0) och en alternativ väg (1), som användare kan omdirigeras till avfarten. Operatören känner till den totala ankomsthastigheten ( A ( t )), kapaciteten på motorvägen ( μ ) och kapaciteten för den alternativa rutten ( μ ₁ ). Från tidpunkten 't ', när motorvägen är överbelastad, börjar några av användarna att flytta till en alternativ rutt. Men när t ₁ är alternativ väg också full av kapacitet. Nu bestämmer operatören antalet fordon(N), som använder alternativ väg. Det optimala antalet fordon ( N ) kan erhållas genom variationskalkyl för att göra marginalkostnaden för varje rutt lika. Det optimala tillståndet är alltså T = T ₁ + ∆ ₁ . I den här grafen kan vi se att kön på den alternativa rutten bör tömmas ∆ ₁ tidsenheter innan den rensas från motorvägen. Denna lösning definierar inte hur vi ska fördela fordon som kommer mellan t ₁ och T ₁ , vi kan bara dra slutsatsen att den optimala lösningen inte är unik. Om operatören vill att motorvägen inte ska vara överbelastad, kan operatören införa trängselavgiften, e ― e ₁ , som är skillnaden mellan den externa effekten av motorväg och alternativ väg. I den här situationen kommer motorvägen att bibehålla fri flödeshastighet, men alternativ väg kommer att vara extremt överbelastad.

Användarjämvikt

Kort sagt, Ett nätverk är i användarjämvikt (UE) när varje förare väljer rutterna i sin lägsta kostnad mellan ursprung och destination oavsett om den totala systemkostnaden minimeras.

Användarens optimala jämvikt förutsätter att alla användare väljer sin egen rutt mot sin destination baserat på den restid som kommer att förbrukas i olika ruttalternativ. Användarna väljer den rutt som kräver minst restid. Den användaroptimala modellen används ofta för att simulera påverkan på trafiktilldelningen av flaskhalsar på motorvägar. När trängseln uppstår på motorvägen kommer det att förlänga förseningstiden för att resa genom motorvägen och skapa en längre restid. Under det användaroptimala antagandet skulle användarna välja att vänta tills restiden på en viss motorväg är lika med restiden på stadsgator, och därmed jämvikt uppnås. Denna jämvikt kallas User Equilibrium, Wardrop Equilibrium eller Nash Equilibrium.

Figur 15. Användarjämviktstrafikmodell

Kärnprincipen för User Equilibrium är att alla använda rutter mellan ett givet OD-par har samma restid. Ett alternativt ruttalternativ är aktiverat att använda när den faktiska restiden i systemet har nått friflödesrestiden på den rutten.

För en motorvägsanvändares optimal modell med tanke på en alternativ rutt, visas en typisk process för trafiktilldelning i figur 15. När trafikbehovet förblir under motorvägskapaciteten förblir fördröjningstiden på motorvägen noll. När trafikbehovet överstiger kapaciteten kommer kön av fordon att dyka upp på motorvägen och fördröjningstiden ökar. En del av användarna kommer att vända sig till stadsgatorna när förseningstiden når skillnaden mellan restiden i fritt flöde på motorvägen och restiden i fritt flöde på stadsgator. Det tyder på att de användare som vistas på motorvägen kommer att spendera lika mycket restid som de som vänder sig till stadens gator. I detta skede förblir restiden på både motorvägen och den alternativa rutten densamma. Denna situation kan upphöra när efterfrågan sjunker under vägkapaciteten, det vill säga restiden på motorvägen börjar minska och alla användare stannar på motorvägen. Summan av delområde 1 och 3 representerar fördelarna genom att tillhandahålla en alternativ väg. Summan av område 4 och område 2 visar den totala förseningskostnaden i systemet, i vilket område 4 är den totala förseningen uppstår på motorvägen och område 2 är den extra förseningen genom att flytta trafik till stadsgator.

Navigationsfunktion i Google Maps kan hänvisas till som en typisk industriell tillämpning av dynamisk trafiktilldelning baserad på användarjämvikt eftersom den ger varje användare ruttalternativet till lägsta kostnad (restid).

Tidsfördröjning

Både User Optimum och System Optimum kan delas in i två kategorier baserat på tillvägagångssättet för tidsfördröjning för deras lösning:

Prediktiv tidsfördröjning

Prediktiv tidsfördröjning förutsätter att användaren av systemet vet exakt hur lång fördröjningen kommer att vara direkt. Prediktiv fördröjning vet när en viss trängselnivå kommer att nås och när fördröjningen av det systemet skulle vara mer än att ta det andra systemet, så beslutet om omdirigering kan fattas i tid. I fordonets räknetidsdiagram är den prediktiva fördröjningen vid tidpunkten t det horisontella linjesegmentet på höger sida av tiden t, mellan ankomst- och avgångskurvan, som visas i figur 16. motsvarande y-koordinat är det nummer n:te fordonet som lämnar systemet vid tidpunkten t.

Reaktiv tidsfördröjning

Reaktiv tidsfördröjning är när användaren inte känner till trafikförhållandena framför sig. Användaren väntar på att uppleva punkten där förseningen observeras och beslutet att omdirigera är en reaktion på den upplevelsen för tillfället. Prediktiv fördröjning ger betydligt bättre resultat än den reaktiva fördröjningsmetoden. I fordonets räknetidsdiagram är den prediktiva fördröjningen vid tidpunkten t det horisontella linjesegmentet på vänster sida av tiden t, mellan ankomst- och avgångskurvan, som visas i figur 16. motsvarande y-koordinat är det n:te fordonet som kommer in i systemet vid tidpunkten t.

Figur 16. Prediktiv och reaktiv tidsfördröjning

Variabel hastighetsbegränsning

Detta är ett kommande tillvägagångssätt för att eliminera stötvågor och öka säkerheten för fordonen. Konceptet bygger på att olycksrisken på en vägbana ökar med hastighetsskillnaden mellan uppströms och nedströms fordon. De två typerna av krockrisk som kan minskas från VSL-implementering är krockar bakifrån och körfältskrockar. Variabla hastighetsgränser försöker homogenisera hastigheten, vilket leder till ett mer konstant flöde. Olika metoder har implementerats av forskare för att bygga en lämplig VSL-algoritm.

Variabla hastighetsgränser tillämpas vanligtvis när sensorer längs vägbanan upptäcker att trafikstockningar eller väderhändelser har överskridit tröskelvärdena. Hastighetsgränsen på vägen kommer sedan att sänkas i steg om 5 km/h genom användning av skyltar ovanför vägbanan (Dynamic Message Signs) som kontrolleras av Department of Transportation. Målet med denna process är att både öka säkerheten genom att minska olyckor och att undvika eller skjuta upp uppkomsten av trängsel på vägbanan. Det idealiska resulterande trafikflödet är långsammare totalt sett, men mindre stop-and-go, vilket resulterar i färre fall av bakifrån och filbyteskrockar. Användningen av VSL:er använder också regelbundet axelbanor som är tillåtna för transport endast under överbelastade stater som denna process syftar till att bekämpa. Behovet av en variabel hastighetsgräns visas av flödesdensitetsdiagrammet till höger.

Hastighets-flödesdiagram för typisk vägbana

I denna figur ("Flödeshastighetsdiagram för en typisk vägbana") representerar kurvans punkt optimal trafikrörelse i både flöde och hastighet. Men bortom denna punkt når färdhastigheten snabbt en tröskel och börjar sjunka snabbt. För att minska den potentiella risken för denna snabba hastighetsminskning, minskar variabla hastighetsgränser hastigheten i en mer gradvis takt (5 mph-steg), vilket gör att förarna får mer tid att förbereda sig och vänja sig vid nedgången på grund av trängsel/väder. Utvecklingen av en enhetlig körhastighet minskar sannolikheten för oregelbundet förarbeteende och därför krockar.

Genom historiska data från VSL-platser har det fastställts att implementering av denna praxis minskar antalet olyckor med 20-30 %.

Utöver säkerhets- och effektivitetsproblem kan VSL:er också ge miljöfördelar som minskade utsläpp, buller och bränsleförbrukning. Detta beror på det faktum att fordon är mer bränslesnåla när de körs konstant, snarare än i ett tillstånd av konstant acceleration och deacceleration som det som vanligtvis finns i överbelastade förhållanden.

Vägkorsningar

Ett stort övervägande i vägkapaciteten hänför sig till utformningen av korsningar. Genom att tillåta långa "vävsektioner" på svagt kurviga vägar i graderade korsningar, kan fordon ofta röra sig över körfält utan att orsaka betydande störningar på flödet. Detta är dock dyrt och tar upp en stor mängd mark, så andra mönster används ofta, särskilt i tätorter eller mycket landsbygdsområden. De flesta stora modeller använder grovsimuleringar för korsningar, men datorsimuleringar är tillgängliga för att modellera specifika uppsättningar av trafikljus, rondeller och andra scenarier där flödet avbryts eller delas med andra typer av trafikanter eller fotgängare. En väl utformad korsning kan möjliggöra betydligt mer trafikflöde vid en rad trafiktätheter under dagen. Genom att matcha en sådan modell med ett "intelligent transportsystem" kan trafik skickas i oavbrutna "paket" av fordon med förutbestämda hastigheter genom en serie av fasade trafikljus. Storbritanniens TRL har utvecklat korsningsmodelleringsprogram för småskaliga lokala system som kan ta hänsyn till detaljerad geometri och siktlinjer; ARCADY för rondeller, PICADY för prioriterade korsningar och OSCADY och TRANSYT för signaler. Många andra programvarupaket för korsningsanalys finns som Sidra och LinSig och Synchro.

Kinematisk vågmodell

Den kinematiska vågmodellen tillämpades först på trafikflödet av Lighthill och Whitham 1955. Deras tvådelade papper utvecklade först teorin om kinematiska vågor med hjälp av vattnets rörelse som ett exempel. Under den andra halvan utvidgade de teorin till att även omfatta trafik på "fulla vägar." Denna artikel handlade i första hand om att utveckla idén om trafikens "puckel" (ökningar i flödet) och deras effekter på hastigheten, särskilt genom flaskhalsar.

Författarna började med att diskutera tidigare synsätt på trafikflödesteori. De noterar att det vid den tiden hade förekommit en del experimentellt arbete, men att "teoretiska förhållningssätt till ämnet [var] i sin linda." En forskare i synnerhet, John Glen Wardrop, var främst oroad över statistiska undersökningsmetoder, såsom medelhastighet i rymden, medelhastighet i tiden och "effekten av ökat flöde vid omkörning" och den resulterande hastighetsminskningen det skulle orsaka. Annan tidigare forskning hade fokuserat på två separata modeller: en relaterad trafikhastighet till trafikflödet och en annan relaterad hastighet till framsteg mellan fordon.

Målet för Lighthill och Whitham, å andra sidan, var att föreslå en ny studiemetod "föreslagen av teorier om flödet om överljudsprojektiler och översvämningsrörelser i floder." Den resulterande modellen skulle fånga båda de ovan nämnda sambanden, hastighet-flöde och hastighet-framväg, i en enda kurva, som skulle "[summa] alla egenskaper hos en vägsträcka som är relevanta för dess förmåga att hantera flödet av överbelastad trafik." Modellen som de presenterade relaterade trafikflöde till koncentration (nu vanligtvis känd som densitet). De skrev, "Teorins grundläggande hypotes är att flödet q (fordon per timme) vid vilken punkt som helst på vägen är en funktion av koncentrationen k (fordon per mil)." Enligt denna modell liknade trafikflödet vattenflödet genom att "Små förändringar i flödet fortplantas tillbaka genom strömmen av fordon längs 'kinematiska vågor', vars hastighet i förhållande till vägen är lutningen på flödesgrafen mot koncentration. ” Författarna inkluderade ett exempel på en sådan graf; denna flöde-mot-koncentration (densitet) plot används fortfarande idag (se figur 3 ovan).

Författarna använde denna flödeskoncentrationsmodell för att illustrera konceptet med stötvågor, som saktar ner fordon som kommer in i dem, och förhållandena som omger dem. De diskuterade också flaskhalsar och korsningar, relaterade båda till deras nya modell. För vart och ett av dessa ämnen inkluderades diagram över flödeskoncentration och tid-rum. Slutligen noterade författarna att det inte fanns någon överenskommen definition av kapacitet och hävdade att den borde definieras som det "maximala flödet som vägen är kapabel till." Lighthill och Whitham insåg också att deras modell hade en betydande begränsning: den var endast lämplig för användning på långa, trånga vägar, eftersom tillvägagångssättet "kontinuerligt flöde" bara fungerar med ett stort antal fordon.

Komponenter i den kinematiska vågmodellen för trafikflödesteori

Den kinematiska vågmodellen för trafikflödesteorin är den enklaste dynamiska trafikflödesmodellen som reproducerar utbredningen av trafikvågor . Den består av tre komponenter: grunddiagrammet , bevarandeekvationen och initiala villkor. Lagen om bevarande är den grundläggande lagen som styr den kinematiska vågmodellen:

${\frac {\partial k}{\partial t}}+{\frac {\partial q}{\partial x}}=0,$

Grunddiagrammet för den kinematiska vågmodellen relaterar trafikflöde med densitet, som ses i figur 3 ovan. Det kan skrivas som:

${q}={F(k)}$

Slutligen måste initiala villkor definieras för att lösa ett problem med hjälp av modellen. En gräns definieras som ${\displaystyle {k(t,x)}} ,$ som representerar densitet som en funktion av tid och position. Dessa gränser tar vanligtvis två olika former, vilket resulterar i initiala värdeproblem (IVPs) och boundary value problem (BVPs). Initiala värdeproblem ger trafiktätheten vid tidpunkten ${t}={0}$ , så att ${k(0,x)}={g( x)}$ , där ${g(x)}$ är den givna densitetsfunktionen. Gränsvärdesproblem ger någon funktion ${g(t)}$ som representerar densiteten vid positionen ${x=0}$ , så att ${k(t,0)}={g(t)}$ . Modellen har många användningsområden i trafikflödet. En av de primära användningsområdena är att modellera trafikflaskhalsar, som beskrivs i följande avsnitt.

Trafikflaskhals

Trafikflaskhalsar är störningar i trafiken på en väg som orsakas antingen på grund av vägdesign, trafikljus eller olyckor. Det finns två generella typer av flaskhalsar, stationära och rörliga flaskhalsar. Stationära flaskhalsar är de som uppstår på grund av en störning som uppstår på grund av en stillastående situation som avsmalning av en vägbana, en olycka. Rörliga flaskhalsar å andra sidan är de fordon eller fordonsbeteende som orsakar störningar i fordonen som är uppströms fordonet. I allmänhet orsakas rörliga flaskhalsar av tunga lastbilar eftersom de är långsamma fordon med mindre acceleration och även kan göra filbyten.7

Orsaker till trafikstockningar i USA

Flaskhalsar (40 %)

Trafikincidenter (25 %)

Arbetszoner (10 %)

Dåligt väder (15%)

Dålig signaltiming (5 %)

Särskilda evenemang / annat (5%)

Flaskhalsar är viktiga överväganden eftersom de påverkar flödet i trafiken, fordonens medelhastigheter. Den främsta konsekvensen av en flaskhals är en omedelbar minskning av kapaciteten på vägbanan. Federal Highway Authority har uppgett att 40 % av all trängsel kommer från flaskhalsar. ^{[ citat behövs ]}

Stationär flaskhals

Bild 18

Den allmänna orsaken till stationära flaskhalsar är körfältsavbrott som uppstår när en flerfilig körbana tappar ett eller flera körfält. Detta gör att fordonstrafiken i slutfilerna går över i de andra körfälten.

Rörlig flaskhals

Som förklarats ovan orsakas rörliga flaskhalsar på grund av långsamma fordon som orsakar störningar i trafiken. Rörliga flaskhalsar kan vara aktiva eller inaktiva flaskhalsar. Om den reducerade kapaciteten (q _u ) orsakad av en rörlig flaskhals är större än den faktiska kapaciteten (μ) nedströms om fordonet, sägs denna flaskhals vara en aktiv flaskhals.

Klassiska trafikflödesteorier

De allmänt accepterade klassiska grunderna och metoderna för trafik- och transportteori är följande:

Modellen Lighthill-Whitham-Richards (LWR) introducerades 1955–56. Daganzo introducerade en celltransmissionsmodell (CTM) som överensstämmer med LWR-modellen.
En instabilitet i trafikflödet som orsakar en växande våg av en lokal minskning av fordonshastigheten. Denna klassiska trafikflödesinstabilitet introducerades 1959–61 i General Motors (GM) bilföljande modell av Herman, Gazis, Montroll, Potts och Rothery. Den klassiska trafikflödesinstabiliteten hos GM-modellen har införlivats i ett stort antal trafikflödesmodeller som Gipps modell, Paynes modell, Newells optimala hastighetsmodell (OV), Wiedemanns modell, Whithams modell, Nagel-Schreckenberg (NaSch) cellulär automat. (CA) modell, Bando et al. OV-modell, Treibers IDM, Krauß-modell, Aw-Rascle-modellen och många andra välkända mikroskopiska och makroskopiska trafikflödesmodeller, som är grunden för trafiksimuleringsverktyg som ofta används av trafikingenjörer och forskare (se t.ex. referenser i recension).
Förståelsen av motorvägskapacitet som ett särskilt värde. Denna förståelse av vägkapacitet infördes troligen 1920–35 (se ). För närvarande antas det att motorvägskapacitet för fritt flöde vid en motorvägsflaskhals är ett stokastiskt värde. I enlighet med den klassiska förståelsen av motorvägskapacitet antas det dock att det vid ett givet ögonblick bara kan finnas ett särskilt värde av denna stokastiska motorvägskapacitet (se referenser i boken).
Wardrops principer för användarjämvikt (UE) och systemoptimum (SO) för optimering och kontroll av trafik- och transportnätverk.

Alternativ: Kerners trefastrafikteori

Tre-fas trafikteori är en alternativ teori om trafikflöde skapad av Boris Kerner i slutet av 1990-talet (för recensioner, se böckerna). Det förmodligen viktigaste resultatet av trefasteorin är att det när som helst finns en rad motorvägskapaciteter med fritt flöde vid en flaskhals. Kapacitetsintervallet ligger mellan vissa maximala och minimala kapaciteter. Utbudet av motorvägskapaciteter för fritt flöde vid flaskhalsen i trefastrafikteori motsäger i grunden klassiska trafikteorier såväl som metoder för trafikledning och trafikkontroll som när som helst antar att det finns en viss deterministisk eller stokastisk motorvägskapacitet för fri trafik . flöde vid flaskhalsen. Icke-specialister som aldrig har lärt sig om trafikfenomen tidigare kan hitta förenklade förklaringar av verkliga uppmätta fordonstrafikfenomen som leder till uppkomsten av Kerners trefastrafikteori i boken; några tekniska tillämpningar av Kerners teori finns i boken.

Newell-Daganzo Merge Models

Diagrammet för Newell-Daganzo sammanslagningsmodell och dess variabler

I tillståndet av trafikflöden som lämnar två grenar av vägbanor och smälter samman till ett enda flöde genom en enda vägbana, blir det en viktig uppgift för trafikingenjörer att bestämma flödena som passerar genom sammanslagningsprocessen och tillståndet för varje gren av vägbanor. Newell -Daganzo-fusionsmodellen är ett bra sätt att lösa dessa problem. Denna enkla modell är resultatet av resultatet av både Gordon Newells beskrivning av sammanslagningsprocessen och Daganzos cellöverföringsmodell . För att kunna tillämpa modellen för att bestämma flödena som lämnar två grenar av vägbanor och statistiken för varje gren av vägbanor, behöver man känna till kapaciteten för de två ingående grenarna av vägbanor, den utgående kapaciteten, kraven för varje gren av vägbanor , och antalet körfält på den enda vägbanan. Sammanslagningsförhållandet kommer att beräknas för att bestämma andelen av de två inflödena när båda grenarna av vägbanan är i trafik under överbelastade förhållanden.

Som kan ses i en förenklad modell av sammanslagningsprocessen definieras systemets utgående kapacitet till μ, kapaciteten för de två ingående grenarna av vägbanor definieras som μ 1 och μ 2 och _kraven för _varje gren av vägbanor definieras som q ₁^D och q ₂^D . q ₁ och q ₂ är utdata från modellen som är de flöden som passerar genom sammanslagningsprocessen. Modellens process är baserad på antagandet att summan av kapaciteterna för de två ingående grenarna av vägbanor är mindre än systemets utgående kapacitet, μ 1 ₊ μ ₂ ≤ μ.

Bilföljande modeller

Bilföljande modeller beskriver hur ett fordon följer ett annat fordon i ett oavbrutet trafikflöde. De är en typ av mikroskopiska trafikflödesmodeller .

Exempel på bilföljande modeller

Newells bilföljande modell
Louis A. Pipes började forska och få erkännande från allmänheten i början av 1950-talet. Pipes bilföljande modell är baserad på en regel för säker körning i California Motor Vehicle Code, och denna modell använde ett antagande om säkert avstånd: en bra regel för att följa ett annat fordon är att tilldela ett avstånd mellan fordon på minst längden av en bil för varje tio mil per timme i fordonshastighet. M
För att fånga de potentiella olinjära effekterna i dynamiken i bilföljande, föreslog GF Newell en olinjär bilföljande modell baserad på empiriska data. Till skillnad från Pipes-modellen som enbart förlitar sig på regler för säker körning, syftar Newells olinjära modell till att fånga den korrekta formen av grundläggande diagram (t.ex. densitet-hastighet, flödeshastighet, densitet-flöde, avstånd-hastighet, pace-headway, etc. ).
Optimal Velocity Model (OVM) introducerades av Bando et al. 1995 baserat på antagandet att varje förare försöker nå den optimala hastigheten enligt skillnaden mellan fordon och hastighetsskillnad mellan föregående fordon.
Intelligent förarmodell används i stor utsträckning i forskningen om Connected Vehicle (CV) och Connected and Autonomous Vehicle (CAV).

Se även

Vidare läsning

En undersökning om det senaste inom trafikflödesmodellering:

N. Bellomo, V. Coscia, M. Delitala, om den matematiska teorin om fordonstrafikflöde I. Fluid Dynamic and Kinetic Modelling, Math. Mod. Meth. App. Sc. Vol. 12, nr 12 (2002) 1801–1843
S. Maerivoet, Modeling Traffic on Motorways: State-of-the-Art, Numerical Data Analysis, and Dynamic Traffic Assignment , Katholieke Universiteit Leuven, 2006
M. Garavello och B. Piccoli, Traffic Flow on Networks, American Institute of Mathematical Sciences (AIMS), Springfield, MO, 2006. s. xvi+243 ISBN 978-1-60133-000-0
Carlos F.Daganzo, "Fundamentals of Transportation and Traffic Operations.", Pergamon-Elsevier, Oxford, Storbritannien (1997)
BS Kerner, Introduktion till Modern Traffic Flow Theory and Control: The Long Road to Three-Phase Traffic Theory , Springer, Berlin, New York 2009
Cassidy, MJ och RL Bertini. "Observationer vid en motorvägsflaskhals." Transport- och trafikteori (1999).
Daganzo, Carlos F. "En enkel trafikanalysprocedur." Nätverk och rumslig ekonomi 1.i (2001): 77–101.
Lindgren, Roger VF "Analys av flödesegenskaper i kötrafik på en tysk motorväg." Portland State University (2005).
Ni, B. och JD Leonard. "Direkta metoder för att bestämma trafikströmskarakteristika per definition." Transportforskningsrekord (2006).

Användbara böcker ur fysisk synvinkel:

M. Treiber och A. Kesting, "Traffic Flow Dynamics", Springer, 2013
BS Kerner, The Physics of Traffic , Springer, Berlin, New York 2004
Trafikflöde på arxiv.org
maj, Adolf. Trafikflöde grunderna . Prentice Hall, Englewood Cliffs, NJ, 1990.
Taylor, Nicholas. Contrams dynamiska trafiktilldelningsmodell TRL 2003

externa länkar

Transportation Research Boards (TRB) femte upplaga av Highway Capacity Manual (HCM 2010)